Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schimmerling, Ernest
2007.
Coherent sequences and threads.
Advances in Mathematics,
Vol. 216,
Issue. 1,
p.
89.
Busche, Daniel
and
Schindler, Ralf
2009.
The strength of choiceless patterns of singular and weakly compact cardinals.
Annals of Pure and Applied Logic,
Vol. 159,
Issue. 1-2,
p.
198.
Schimmerling, Ernest
2010.
Handbook of Set Theory.
p.
1685.
Apter, Arthur W.
2011.
A remark on the tree property in a choiceless context.
Archive for Mathematical Logic,
Vol. 50,
Issue. 5-6,
p.
585.
Larson, Jean A.
2012.
Sets and Extensions in the Twentieth Century.
Vol. 6,
Issue. ,
p.
145.
Daghighi, Ali Sadegh
and
Pourmahdian, Massoud
2016.
The definable tree property for successors of cardinals.
Archive for Mathematical Logic,
Vol. 55,
Issue. 5-6,
p.
785.
Gitik, Moti
Schindler, Ralf
and
Shelah, Saharon
2017.
Logic Colloquium '02.
p.
172.
Honzik, Radek
and
Stejskalová, Šárka
2018.
The tree property and the continuum function below .
Mathematical Logic Quarterly,
Vol. 64,
Issue. 1-2,
p.
89.
Kechris, Alexander S.
Löwe, Benedikt
and
Steel, John R.
2020.
Large Cardinals, Determinacy and Other Topics.
Stejskalová, Šárka
2021.
Easton's theorem for the tree property below ℵ.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 7,
p.
102974.


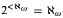 , then for all
, then for all 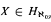 and
and 