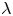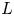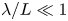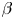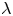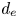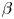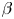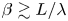1. Introduction
Answering the question of when a plasma can be described adequately by fluid equations is fundamental for a comprehensive understanding of plasma dynamics. It is well known that some physical effects in plasmas – for example, Landau damping – specifically require a fully kinetic description in terms of distribution functions of the plasma's constituent particles (Landau Reference Landau1946). However, for many other plasma processes, a detailed description of the underlying particle distribution provides little additional understanding of the essential physics governing that process. Characterising such processes with fluid equations, which describe the evolution of macroscopic physical quantities such as density, fluid velocity and temperature, often simplifies the description and therefore aids understanding. Fluid equations are also easier to solve numerically than kinetic equations: the latter reside in six-dimensional phase space (and time), with three additional dimensions – the velocity space – when compared with the former. The underlying difficulty associated with determining when a plasma is a fluid is finding a closed set of equations in the macroscopic plasma variables. The derivation of fluid equations from the Maxwell–Vlasov–Landau equations governing the evolution of the plasma's distribution functions is carried out by taking moments (that is, integrating the governing equations and their outer products with velocity ![]() $\boldsymbol {v}$ over velocity space). However, the resulting equations are not closed: the evolution equation of the zeroth-order moment (density) requires knowledge of the evolution of the first-order moment, the evolution equation for the first-order moment needs the second-order moment and so on. For plasma-fluid equations to be able to describe the evolution of a plasma without reference to that plasma's underlying distribution functions, a closure hypothesis or an approximation relating higher-order moments to lower ones is required.
$\boldsymbol {v}$ over velocity space). However, the resulting equations are not closed: the evolution equation of the zeroth-order moment (density) requires knowledge of the evolution of the first-order moment, the evolution equation for the first-order moment needs the second-order moment and so on. For plasma-fluid equations to be able to describe the evolution of a plasma without reference to that plasma's underlying distribution functions, a closure hypothesis or an approximation relating higher-order moments to lower ones is required.
For a collisional plasma – i.e. one in which the mean free paths ![]() $\lambda _{s}$ and collision times
$\lambda _{s}$ and collision times ![]() $\tau _s$ of the ions and electrons (
$\tau _s$ of the ions and electrons (![]() $s = i, e$) are much smaller than the typical length scale
$s = i, e$) are much smaller than the typical length scale ![]() $L$ and time scale
$L$ and time scale ![]() $\tau _L$ on which macroscopic properties of the plasma change – there is a procedure for achieving such a closure: the Chapman–Enskog (CE) expansion (Chapman & Cowling Reference Chapman and Cowling1970; Enskog Reference Enskog1917; Cercignani Reference Cercignani1988). It is assumed that, in a collisional plasma, the small perturbations of the distribution functions away from a Maxwellian equilibrium have typical size
$\tau _L$ on which macroscopic properties of the plasma change – there is a procedure for achieving such a closure: the Chapman–Enskog (CE) expansion (Chapman & Cowling Reference Chapman and Cowling1970; Enskog Reference Enskog1917; Cercignani Reference Cercignani1988). It is assumed that, in a collisional plasma, the small perturbations of the distribution functions away from a Maxwellian equilibrium have typical size ![]() $\epsilon \sim \lambda _{s}/L \sim \tau _s/\tau _L \ll 1$ (assuming sonic motions, and
$\epsilon \sim \lambda _{s}/L \sim \tau _s/\tau _L \ll 1$ (assuming sonic motions, and ![]() $\lambda _i \sim \lambda _e$). Since the perturbation is small, its form can be determined explicitly by performing an asymptotic expansion of the Maxwell–Vlasov–Landau equations. Once the underlying distribution is known, the relevant moments can be calculated – in particular, the momentum and heat fluxes are the second- and third-order moments of the
$\lambda _i \sim \lambda _e$). Since the perturbation is small, its form can be determined explicitly by performing an asymptotic expansion of the Maxwell–Vlasov–Landau equations. Once the underlying distribution is known, the relevant moments can be calculated – in particular, the momentum and heat fluxes are the second- and third-order moments of the ![]() ${O}(\epsilon )$ non-Maxwellian component of the distribution function. The CE expansion applied to a two-species magnetised plasma was worked out by Braginskii (Reference Braginskii1965). Subsequent studies have refined and extended various aspects of his calculation (Epperlein Reference Epperlein1984; Mikhailovskii & Tsypin Reference Mikhailovskii and Tsypin1984; Epperlein & Haines Reference Epperlein and Haines1986; Helander, Krasheninnikov & Catto Reference Helander, Krasheninnikov and Catto1994; Simakov & Catto Reference Simakov and Catto2004). In this paper, we will refer to the distribution functions associated with the CE expansion as CE distribution functions, and plasmas with particle distribution functions given by CE distribution functions as CE plasmas.
${O}(\epsilon )$ non-Maxwellian component of the distribution function. The CE expansion applied to a two-species magnetised plasma was worked out by Braginskii (Reference Braginskii1965). Subsequent studies have refined and extended various aspects of his calculation (Epperlein Reference Epperlein1984; Mikhailovskii & Tsypin Reference Mikhailovskii and Tsypin1984; Epperlein & Haines Reference Epperlein and Haines1986; Helander, Krasheninnikov & Catto Reference Helander, Krasheninnikov and Catto1994; Simakov & Catto Reference Simakov and Catto2004). In this paper, we will refer to the distribution functions associated with the CE expansion as CE distribution functions, and plasmas with particle distribution functions given by CE distribution functions as CE plasmas.
However, the theory constructed as outlined above is incomplete. For the CE expansion to provide an adequate fluid closure, the resulting distribution functions must be stable to all kinetic instabilities with length scales shorter than the longest mean free path, and time scales shorter than the macroscopic plasma time scale ![]() $\tau _L$. Such instabilities (if present) are known as microinstabilities. We emphasise that these microinstabilities should be distinguished conceptually from instabilities describable by the closed set of plasma-fluid equations: for example, Rayleigh–Taylor (Rayleigh Reference Rayleigh1883; Taylor Reference Taylor1950; Takabe et al. Reference Takabe, Mima, Montierth and Morse1985; Kull Reference Kull1991), magnetorotational (Balbus & Hawley Reference Balbus and Hawley1991; Hawley & Balbus Reference Hawley and Balbus1991), magnetoviscous (Quataert, Dorland & Hammett Reference Quataert, Dorland and Hammett2002; Balbus Reference Balbus2004; Islam & Balbus Reference Islam and Balbus2005) or magnetothermal/heat-flux-driven buoyancy instabilities (Balbus Reference Balbus2000, Reference Balbus2001; Quataert Reference Quataert2008; Kunz Reference Kunz2011). Kinetic microinstabilities should also be distinguished from the small-scale instabilities that arise in solving higher-order
$\tau _L$. Such instabilities (if present) are known as microinstabilities. We emphasise that these microinstabilities should be distinguished conceptually from instabilities describable by the closed set of plasma-fluid equations: for example, Rayleigh–Taylor (Rayleigh Reference Rayleigh1883; Taylor Reference Taylor1950; Takabe et al. Reference Takabe, Mima, Montierth and Morse1985; Kull Reference Kull1991), magnetorotational (Balbus & Hawley Reference Balbus and Hawley1991; Hawley & Balbus Reference Hawley and Balbus1991), magnetoviscous (Quataert, Dorland & Hammett Reference Quataert, Dorland and Hammett2002; Balbus Reference Balbus2004; Islam & Balbus Reference Islam and Balbus2005) or magnetothermal/heat-flux-driven buoyancy instabilities (Balbus Reference Balbus2000, Reference Balbus2001; Quataert Reference Quataert2008; Kunz Reference Kunz2011). Kinetic microinstabilities should also be distinguished from the small-scale instabilities that arise in solving higher-order ![]() $({O}(\epsilon ^2)$) fluid equations obtained from the CE asymptotic expansion (for neutral fluids, these are called the Burnett equations – see García-Colín, Velasco & Uribe Reference García-Colín, Velasco and Uribe2008). Such instabilities are not physical because they arise at scales where the equations themselves do not apply (Bobylev Reference Bobylev1982). Fluid instabilities do not call into question the validity of the fluid equations themselves; in contrast, if microinstabilities occur, the plasma-fluid equations obtained through the closure hypothesis are physically invalid, irrespective of their own stability.
$({O}(\epsilon ^2)$) fluid equations obtained from the CE asymptotic expansion (for neutral fluids, these are called the Burnett equations – see García-Colín, Velasco & Uribe Reference García-Colín, Velasco and Uribe2008). Such instabilities are not physical because they arise at scales where the equations themselves do not apply (Bobylev Reference Bobylev1982). Fluid instabilities do not call into question the validity of the fluid equations themselves; in contrast, if microinstabilities occur, the plasma-fluid equations obtained through the closure hypothesis are physically invalid, irrespective of their own stability.
Microinstabilities have been studied in depth for a wide range of classical plasmas by many authors; see, for e.g. Davidson (Reference Davidson1983), Gary (Reference Gary1993) and Hasegawa (Reference Hasegawa2012) for three different general perspectives on microinstability theory. Although it can be shown that a Maxwellian distribution is always immune to such instabilities (Bernstein Reference Bernstein1958; Krall & Trivelpiece Reference Krall and Trivelpiece1973), anisotropic distribution functions are often not (Kahn Reference Kahn1962; Furth Reference Furth1963; Kalman, Montes & Quemada Reference Kalman, Montes and Quemada1968). A notable example is the Weibel instability, which occurs in counter-streaming unmagnetised plasmas (Fried Reference Fried1959; Weibel Reference Weibel1959). The linear theory of such instabilities is generally well known (for modern reviews, see Lazar, Schlickeiser & Poedts Reference Lazar, Schlickeiser and Poedts2009; Ibscher, Lazar & Schlickeiser Reference Ibscher, Lazar and Schlickeiser2012). Microinstabilities in magnetised plasma have also been comprehensively studied. The ion firehose and mirror instabilities are known to occur in plasmas with sufficient ion-pressure anisotropy and large enough plasma ![]() $\beta$ (Chandrasekhar, Kaufman & Watson Reference Chandrasekhar, Kaufman and Watson1958; Parker Reference Parker1958; Vedenov & Sagdeev Reference Vedenov and Sagdeev1958; Hasegawa Reference Hasegawa1969; Hall Reference Hall1981; Hellinger Reference Hellinger2007), while electron-pressure anisotropy can also result in microinstabilities of various types (Kennel & Petschek Reference Kennel and Petschek1966; Hollweg & Völk Reference Hollweg and Völk1970; Gary & Madland Reference Gary and Madland1985).
$\beta$ (Chandrasekhar, Kaufman & Watson Reference Chandrasekhar, Kaufman and Watson1958; Parker Reference Parker1958; Vedenov & Sagdeev Reference Vedenov and Sagdeev1958; Hasegawa Reference Hasegawa1969; Hall Reference Hall1981; Hellinger Reference Hellinger2007), while electron-pressure anisotropy can also result in microinstabilities of various types (Kennel & Petschek Reference Kennel and Petschek1966; Hollweg & Völk Reference Hollweg and Völk1970; Gary & Madland Reference Gary and Madland1985).
A number of authors have noted that microinstabilities, if present, will have a significant effect on the macroscopic transport properties of plasmas (Kahn Reference Kahn1964; Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005, Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008; Melville, Schekochihin & Kunz Reference Melville, Schekochihin and Kunz2016; Riquelme, Quataert & Verscharen Reference Riquelme, Quataert and Verscharen2016; Komarov et al. Reference Komarov, Churazov, Kunz and Schekochihin2016, Reference Komarov, Schekochihin, Churazov and Spitkovsky2018; Roberg-Clark et al. Reference Roberg-Clark, Drake, Reynolds and Swisdak2018a; Drake et al. Reference Drake, Pfrommer, Reynolds, Ruszkowski, Swisdak, Einarsson, Thomas, Hassam and Roberg-Clark2021). Typically (although not always), once the small-scale magnetic and electric fields associated with microinstabilities have grown, they will start to scatter particles, which in turn will alter the plasma's distribution functions. This has micro- and macroscopic consequences for plasma behaviour. From the microscopic perspective, it changes the course of the evolution of the microinstabilities themselves – by e.g. reducing the anisotropy of the underlying particle distribution functions (Hellinger et al. Reference Hellinger, Trávníček, Decyk and Schriver2014; Riquelme, Quataert & Verscharen Reference Riquelme, Quataert and Verscharen2018). From the macroscopic perspective, the changes to the distribution functions will alter both heat and momentum fluxes in the plasma (which, as previously mentioned, are determined by non-Maxwellian terms in the distribution function). In this picture, a plasma subject to microinstabilities in some sense generates its own effective anomalous collisionality (Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008; Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014; Mogavero & Schekochihin Reference Mogavero and Schekochihin2014; Squire et al. Reference Squire, Kunz, Quataert and Schekochihin2017; Kunz et al. Reference Kunz, Squire, Schekochihin and Quataert2020). The typical values of the altered fluxes attained must depend on the saturated state of microinstabilities (Schekochihin et al. Reference Schekochihin, Cowley, Rincon and Rosin2010). Exploring the mechanisms leading to saturation of both unmagnetised, Weibel-type instabilities (e.g. Davidson et al. Reference Davidson, Hammer, Haber and Wagner1972; Lemons, Winske & Gary Reference Lemons, Winske and Gary1979; Califano et al. Reference Califano, Pegoraro, Bulanov and Mangeney1998; Califano, Cecchi & Chiuderi Reference Califano, Cecchi and Chiuderi2002; Kato Reference Kato2005; Pokhotelov & Amariutei Reference Pokhotelov and Amariutei2011; Ruyer et al. Reference Ruyer, Gremillet, Debayle and Bonnaud2015) and magnetised instabilities (e.g. Kuznetsov, Passot & Sulem Reference Kuznetsov, Passot and Sulem2007; Pokhotelov et al. Reference Pokhotelov, Sagdeev, Balikhin, Onishchenko and Fedun2008; Rosin et al. Reference Rosin, Schekochihin, Rincon and Cowley2011; Rincon, Schekochihin & Cowley Reference Rincon, Schekochihin and Cowley2015; Riquelme, Quataert & Verscharen Reference Riquelme, Quataert and Verscharen2015) continues to be an active research area. Simulation results (Hellinger et al. Reference Hellinger, Kuznetsov, Passot, Sulem and Trávníček2009; Guo, Sironi & Narayan Reference Guo, Sironi and Narayan2014; Kunz et al. Reference Kunz, Schekochihin and Stone2014; Melville et al. Reference Melville, Schekochihin and Kunz2016; Riquelme et al. Reference Riquelme, Quataert and Verscharen2016; Guo, Sironi & Narayan Reference Guo, Sironi and Narayan2018; Bott et al. Reference Bott, Arzamasskiy, Kunz, Quataert and Squire2021a) support the claim that the saturation amplitude of such microinstabilities is typically such that the plasma maintains itself close to marginality of the relevant instability.
Do these kinetic instabilities afflict the CE distribution function? Naively, it might be assumed not, since it is ‘almost’ Maxwellian. However, it turns out that, provided the plasma ![]() $\beta$ is sufficiently high, small distortions from a Maxwellian can be sufficient to lead to instability. Instabilities of a CE distribution function in an unmagnetised plasma were first explored by Kahn (Reference Kahn1964), who considered a collisional electron plasma (mean free path
$\beta$ is sufficiently high, small distortions from a Maxwellian can be sufficient to lead to instability. Instabilities of a CE distribution function in an unmagnetised plasma were first explored by Kahn (Reference Kahn1964), who considered a collisional electron plasma (mean free path ![]() $\lambda _e$) with macroscopic variations in density, temperature and velocity (scale
$\lambda _e$) with macroscopic variations in density, temperature and velocity (scale ![]() ${\sim }L$). He showed that the CE distribution function in such a plasma would have two non-Maxwellian terms of order
${\sim }L$). He showed that the CE distribution function in such a plasma would have two non-Maxwellian terms of order ![]() $\lambda _e/L$ – an antisymmetric term associated with heat flux, and another term associated with velocity shear – and that the latter term would result in the so-called transverse instability. Kahn (Reference Kahn1964) also claimed that this instability would lead to a significant change in the plasma viscosity, and other transport coefficients. Albright (Reference Albright1970a,Reference Albrightb) further developed the theory of the transverse instability, including a quasi-linear theory resulting in isotropisation of the underlying electron distribution function.
$\lambda _e/L$ – an antisymmetric term associated with heat flux, and another term associated with velocity shear – and that the latter term would result in the so-called transverse instability. Kahn (Reference Kahn1964) also claimed that this instability would lead to a significant change in the plasma viscosity, and other transport coefficients. Albright (Reference Albright1970a,Reference Albrightb) further developed the theory of the transverse instability, including a quasi-linear theory resulting in isotropisation of the underlying electron distribution function.
The stability of the CE distribution function was later considered by Ramani & Laval (Reference Ramani and Laval1978). They found that in an initially unmagnetised two-species plasma supporting a fluid-scale electron-temperature gradient (scale ![]() $L_T$, no flow shear), the second-order terms (in
$L_T$, no flow shear), the second-order terms (in ![]() $\lambda /L_T$) in the electron distribution function could result in the formation of unstable waves, with typical real frequencies
$\lambda /L_T$) in the electron distribution function could result in the formation of unstable waves, with typical real frequencies ![]() $\varpi \propto \lambda _{e}/L_T$, and growth rates
$\varpi \propto \lambda _{e}/L_T$, and growth rates ![]() $\gamma _{\rm RL} \propto (\lambda _{e}/L_T)^2$. Similarly to Kahn (Reference Kahn1964), they argued that the presence of such instabilities would suppress the macroscopic heat flux in the plasma (which in a collisional plasma is carried predominantly by electrons). This particular instability has also been proposed as an explanation for the origin of the cosmic magnetic field (Okabe & Hattori Reference Okabe and Hattori2003). Subsequent authors have explored further the idea that non-Maxwellian components of the electron distribution function required to support a macroscopic heat flux can lead to kinetic instability. Levinson & Eichler (Reference Levinson and Eichler1992) considered the effect of introducing a uniform, macroscopic magnetic field into the same problem, and found that a faster instability feeding off first-order heat-flux terms in the CE distribution function – the whistler instability – arose at the electron-Larmor scale, with
$\gamma _{\rm RL} \propto (\lambda _{e}/L_T)^2$. Similarly to Kahn (Reference Kahn1964), they argued that the presence of such instabilities would suppress the macroscopic heat flux in the plasma (which in a collisional plasma is carried predominantly by electrons). This particular instability has also been proposed as an explanation for the origin of the cosmic magnetic field (Okabe & Hattori Reference Okabe and Hattori2003). Subsequent authors have explored further the idea that non-Maxwellian components of the electron distribution function required to support a macroscopic heat flux can lead to kinetic instability. Levinson & Eichler (Reference Levinson and Eichler1992) considered the effect of introducing a uniform, macroscopic magnetic field into the same problem, and found that a faster instability feeding off first-order heat-flux terms in the CE distribution function – the whistler instability – arose at the electron-Larmor scale, with ![]() $\gamma _{{\rm whistler},T} \propto \lambda _{e}/L_T$. A quasi-linear theory of this instability was subsequently constructed by Pistinner & Eichler (Reference Pistinner and Eichler1998). Both Levinson & Eichler (Reference Levinson and Eichler1992) and Pistinner & Eichler (Reference Pistinner and Eichler1998) proposed that the instability at saturation would result in a suppressed heat flux (see also Gary & Li Reference Gary and Li2000). More recently, the whistler instability has been studied in simulations of high-
$\gamma _{{\rm whistler},T} \propto \lambda _{e}/L_T$. A quasi-linear theory of this instability was subsequently constructed by Pistinner & Eichler (Reference Pistinner and Eichler1998). Both Levinson & Eichler (Reference Levinson and Eichler1992) and Pistinner & Eichler (Reference Pistinner and Eichler1998) proposed that the instability at saturation would result in a suppressed heat flux (see also Gary & Li Reference Gary and Li2000). More recently, the whistler instability has been studied in simulations of high-![]() $\beta$ plasma – with two groups independently finding both the onset of instability at electron scales, and evidence of a suppression of heat flux (Roberg-Clark et al. Reference Roberg-Clark, Drake, Reynolds and Swisdak2016, Reference Roberg-Clark, Drake, Reynolds and Swisdak2018a; Komarov et al. Reference Komarov, Schekochihin, Churazov and Spitkovsky2018; Roberg-Clark et al. Reference Roberg-Clark, Drake, Swisdak and Reynolds2018b). Drake et al. (Reference Drake, Pfrommer, Reynolds, Ruszkowski, Swisdak, Einarsson, Thomas, Hassam and Roberg-Clark2021) constructed a theoretical model for whistler-regulated heat transport based on a set of reasonable assumptions that were motivated by these prior simulations.
$\beta$ plasma – with two groups independently finding both the onset of instability at electron scales, and evidence of a suppression of heat flux (Roberg-Clark et al. Reference Roberg-Clark, Drake, Reynolds and Swisdak2016, Reference Roberg-Clark, Drake, Reynolds and Swisdak2018a; Komarov et al. Reference Komarov, Schekochihin, Churazov and Spitkovsky2018; Roberg-Clark et al. Reference Roberg-Clark, Drake, Swisdak and Reynolds2018b). Drake et al. (Reference Drake, Pfrommer, Reynolds, Ruszkowski, Swisdak, Einarsson, Thomas, Hassam and Roberg-Clark2021) constructed a theoretical model for whistler-regulated heat transport based on a set of reasonable assumptions that were motivated by these prior simulations.
The possibility of microinstabilities associated with the ion CE distribution function was also considered by Schekochihin et al. (Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005), who found that weakly collisional, magnetised plasma undergoing subsonic, turbulent shearing motions can be linearly unstable to firehose and mirror instabilities at sufficiently high ![]() $\beta _i$ (where
$\beta _i$ (where ![]() $\beta _i$ is the ion plasma beta). This is because the shearing motions give rise to an ion-pressure anisotropy
$\beta _i$ is the ion plasma beta). This is because the shearing motions give rise to an ion-pressure anisotropy ![]() $\varDelta _i \sim \lambda _i^2/L_V^2$, where
$\varDelta _i \sim \lambda _i^2/L_V^2$, where ![]() $L_V$ is the length scale associated with the shearing motions. For
$L_V$ is the length scale associated with the shearing motions. For ![]() $|\varDelta _i| \gtrsim \beta _i^{-1}$, the mirror- and firehose-instability thresholds can be crossed (the mirror instability is trigged by sufficiently positive pressure anisotropy, the firehose instability by negative pressure anisotropy). Beyond its threshold, the maximum firehose-instability growth rate
$|\varDelta _i| \gtrsim \beta _i^{-1}$, the mirror- and firehose-instability thresholds can be crossed (the mirror instability is trigged by sufficiently positive pressure anisotropy, the firehose instability by negative pressure anisotropy). Beyond its threshold, the maximum firehose-instability growth rate ![]() $\gamma _{\rm fire}$ was found to satisfy
$\gamma _{\rm fire}$ was found to satisfy ![]() $\gamma _{\rm fire} \propto |\varDelta _i+2/\beta _i|^{1/2}$, whilst for the mirror instability, the maximum growth rate was
$\gamma _{\rm fire} \propto |\varDelta _i+2/\beta _i|^{1/2}$, whilst for the mirror instability, the maximum growth rate was ![]() $\gamma _{\rm mirr} \propto \varDelta _i-1/\beta _i$. Such destabilisation of shearing motions was confirmed numerically by Kunz et al. (Reference Kunz, Schekochihin and Stone2014), followed by many others (e.g. Riquelme et al. Reference Riquelme, Quataert and Verscharen2015, Reference Riquelme, Quataert and Verscharen2016, Reference Riquelme, Quataert and Verscharen2018; Melville et al. Reference Melville, Schekochihin and Kunz2016).
$\gamma _{\rm mirr} \propto \varDelta _i-1/\beta _i$. Such destabilisation of shearing motions was confirmed numerically by Kunz et al. (Reference Kunz, Schekochihin and Stone2014), followed by many others (e.g. Riquelme et al. Reference Riquelme, Quataert and Verscharen2015, Reference Riquelme, Quataert and Verscharen2016, Reference Riquelme, Quataert and Verscharen2018; Melville et al. Reference Melville, Schekochihin and Kunz2016).
In this paper, we examine the criteria for the CE distribution function to be stable to microinstabilities at collisionless scales – i.e. at ![]() $k \lambda _s \gg 1$ (where
$k \lambda _s \gg 1$ (where ![]() $k$ is the microinstability wavenumber), and
$k$ is the microinstability wavenumber), and ![]() $\gamma \tau _L \gg 1$. In a two-species plasma with a fixed mass ratio
$\gamma \tau _L \gg 1$. In a two-species plasma with a fixed mass ratio ![]() $\mu _e \equiv m_e/m_i$,
$\mu _e \equiv m_e/m_i$, ![]() $T_e = T_i$ and an ion charge
$T_e = T_i$ and an ion charge ![]() $Z_i$ that is not very large, these criteria turn out to be relationships between three dimensionless parameters:
$Z_i$ that is not very large, these criteria turn out to be relationships between three dimensionless parameters: ![]() $\lambda /L$,
$\lambda /L$, ![]() $d_e/L$ and
$d_e/L$ and ![]() $\beta$, where
$\beta$, where ![]() $\lambda \equiv \lambda _e = Z_i^2 \lambda_i$ is the mean free path for both ions and electrons in a hydrogen plasma, and
$\lambda \equiv \lambda _e = Z_i^2 \lambda_i$ is the mean free path for both ions and electrons in a hydrogen plasma, and ![]() $d_e$ is the electron inertial scale. The first criterion (which we refer to as the
$d_e$ is the electron inertial scale. The first criterion (which we refer to as the ![]() $\beta$-stabilisation condition) is that the ratio
$\beta$-stabilisation condition) is that the ratio ![]() $\lambda /L$ be much smaller than the reciprocal of the plasma
$\lambda /L$ be much smaller than the reciprocal of the plasma ![]() $\beta$, viz.
$\beta$, viz. ![]() $\lambda \beta /L \ll 1$. This condition arises because the microinstabilities discussed in this paper are stabilised (usually by Lorentz forces) at sufficiently low
$\lambda \beta /L \ll 1$. This condition arises because the microinstabilities discussed in this paper are stabilised (usually by Lorentz forces) at sufficiently low ![]() $\beta$. The second criterion (the collisional-stabilisation condition) is that the characteristic wavenumber
$\beta$. The second criterion (the collisional-stabilisation condition) is that the characteristic wavenumber ![]() $k_{\rm {peak}}$ of the fastest-growing microinstability in the absence of collisional effects be comparable to (or smaller than) the reciprocal of the mean free path:
$k_{\rm {peak}}$ of the fastest-growing microinstability in the absence of collisional effects be comparable to (or smaller than) the reciprocal of the mean free path: ![]() $k_{\rm {peak}} \lambda \lesssim 1$. Unlike the
$k_{\rm {peak}} \lambda \lesssim 1$. Unlike the ![]() $\beta$-stabilisation condition, we do not justify this condition rigorously, because our calculations are only valid for wavenumbers
$\beta$-stabilisation condition, we do not justify this condition rigorously, because our calculations are only valid for wavenumbers ![]() $k$ such that
$k$ such that ![]() $k \lambda \gg 1$; thus, we cannot say anything definitive about the
$k \lambda \gg 1$; thus, we cannot say anything definitive about the ![]() $k \lambda \lesssim 1$ regime. We do, however, show that another, more restrictive stabilisation condition that one might naively expect to exist on account of collisions – that microinstabilities cannot occur if their growth rate
$k \lambda \lesssim 1$ regime. We do, however, show that another, more restrictive stabilisation condition that one might naively expect to exist on account of collisions – that microinstabilities cannot occur if their growth rate ![]() $\gamma$ is smaller than the collision frequency (viz.
$\gamma$ is smaller than the collision frequency (viz. ![]() $\gamma \tau _s \lesssim 1$) – does not, in fact, apply to the most significant microinstabilities in CE plasma. There are good physical reasons to believe that the CE distribution function is stable against collisionless microinstabilities if the collisional-stabilisation condition
$\gamma \tau _s \lesssim 1$) – does not, in fact, apply to the most significant microinstabilities in CE plasma. There are good physical reasons to believe that the CE distribution function is stable against collisionless microinstabilities if the collisional-stabilisation condition ![]() $k_{\rm {peak}} \lambda \lesssim 1$ is satisfied: not least that the typical growth time of the fastest microinstability in CE plasma (calculated neglecting collisional damping of microinstabilities) becomes comparable to the macroscopic evolution time scale
$k_{\rm {peak}} \lambda \lesssim 1$ is satisfied: not least that the typical growth time of the fastest microinstability in CE plasma (calculated neglecting collisional damping of microinstabilities) becomes comparable to the macroscopic evolution time scale ![]() $\tau _L$. We thus assume the validity of the collisional-stabilisation condition throughout this paper. How
$\tau _L$. We thus assume the validity of the collisional-stabilisation condition throughout this paper. How ![]() $k_{\rm {peak}}$ relates to the other physical parameters is in general somewhat complicated; however, typically, the collisional-stabilisation condition can be written as a lower bound on the ratio
$k_{\rm {peak}}$ relates to the other physical parameters is in general somewhat complicated; however, typically, the collisional-stabilisation condition can be written as a lower bound on the ratio ![]() $d_e/L$. For example, in the limit of very high
$d_e/L$. For example, in the limit of very high ![]() $\beta$, it is
$\beta$, it is ![]() $d_e/L > (m_e/m_i)^{-1/6} (\lambda /L)^{2/3}$ (see § 4.2).
$d_e/L > (m_e/m_i)^{-1/6} (\lambda /L)^{2/3}$ (see § 4.2).
If both the ![]() $\beta$-stabilisation and collisional-stabilisation conditions are violated, we demonstrate that CE plasma will be subject to at least one microinstability, and quite possibly multiple microinstabilities across a wide range of scales. Some of these microinstabilities are thresholdless – that is, without including collisional effects, they will occur for CE distributions departing from a Maxwellian distribution by an asymptotically small amount. Note that all significant microinstabilities associated with the CE distribution function are ‘low frequency’: their growth rate
$\beta$-stabilisation and collisional-stabilisation conditions are violated, we demonstrate that CE plasma will be subject to at least one microinstability, and quite possibly multiple microinstabilities across a wide range of scales. Some of these microinstabilities are thresholdless – that is, without including collisional effects, they will occur for CE distributions departing from a Maxwellian distribution by an asymptotically small amount. Note that all significant microinstabilities associated with the CE distribution function are ‘low frequency’: their growth rate ![]() $\gamma$ satisfies
$\gamma$ satisfies ![]() $\gamma \ll k v_{\mathrm {th}s}$, where
$\gamma \ll k v_{\mathrm {th}s}$, where ![]() $k$ is the typical wavenumber of the instability, and
$k$ is the typical wavenumber of the instability, and ![]() $v_{\mathrm {th}s}$ the thermal velocity of the particles of species
$v_{\mathrm {th}s}$ the thermal velocity of the particles of species ![]() $s$. This property enables a small anisotropy of the distribution function to create forces capable of driving microinstabilities (see § 2.5).
$s$. This property enables a small anisotropy of the distribution function to create forces capable of driving microinstabilities (see § 2.5).
In this paper, we characterise all significant microinstabilities that arise at different values of ![]() $\lambda /L$,
$\lambda /L$, ![]() $\beta$ and
$\beta$ and ![]() $d_e/L$ for a particular form of the CE distribution function appropriate for a strongly magnetised plasma – that is, a plasma where the Larmor radii of ions and electrons are much smaller than the corresponding mean free paths of these particles. We treat this particular case because of its importance to astrophysical systems, which almost always possess macroscopic magnetic fields of sufficient strength to magnetise their constituent particles (Schekochihin & Cowley Reference Schekochihin and Cowley2006). Our characterisation of microinstabilities focuses on providing the maximum microinstability growth rates, as well as the wavenumbers at which this growth occurs. We find that there exist two general classes of microinstabilities: those driven by the non-Maxwellian component of the CE distribution associated with temperature gradients, and those driven by the non-Maxwellian component associated with bulk velocity gradients (‘shear’). We refer to these two non-Maxwellian terms (which exist for both the ion and electron CE distribution functions) as the CE temperature-gradient terms and the CE shear terms, respectively. Microinstabilities driven by the CE temperature-gradient terms are called the CE temperature-gradient-driven (CET) microinstabilities, while those driven by the CE shear terms are the CE shear-driven (CES) microinstabilities.
$d_e/L$ for a particular form of the CE distribution function appropriate for a strongly magnetised plasma – that is, a plasma where the Larmor radii of ions and electrons are much smaller than the corresponding mean free paths of these particles. We treat this particular case because of its importance to astrophysical systems, which almost always possess macroscopic magnetic fields of sufficient strength to magnetise their constituent particles (Schekochihin & Cowley Reference Schekochihin and Cowley2006). Our characterisation of microinstabilities focuses on providing the maximum microinstability growth rates, as well as the wavenumbers at which this growth occurs. We find that there exist two general classes of microinstabilities: those driven by the non-Maxwellian component of the CE distribution associated with temperature gradients, and those driven by the non-Maxwellian component associated with bulk velocity gradients (‘shear’). We refer to these two non-Maxwellian terms (which exist for both the ion and electron CE distribution functions) as the CE temperature-gradient terms and the CE shear terms, respectively. Microinstabilities driven by the CE temperature-gradient terms are called the CE temperature-gradient-driven (CET) microinstabilities, while those driven by the CE shear terms are the CE shear-driven (CES) microinstabilities.
As expected, within this general microinstability classification scheme, we recover a number of previously identified microinstabilities, including the (electron-shear-driven) transverse instability (which we discuss in §§ 4.3.3 and 4.4.9), the whistler instability (§ 4.3.2), the electron mirror instability (§ 4.3.4), the electron firehose instability (§§ 4.4.6 and 4.4.7), the ordinary-mode instability (§ 4.4.11), the (electron-temperature-gradient-driven) whistler heat-flux instability (§§ 3.3.1 and 3.3.2) and the (ion-shear-driven) mirror (§ 4.3.1) and firehose (§§ 4.4.1, 4.4.2, 4.4.3, 4.4.4 and 4.4.5) instabilities. We also find four microinstabilities that, to our knowledge, have not been previously discovered: two ion-temperature-gradient-driven ones at ion Larmor scales – the slow-hydromagnetic-wave instability (§ 3.3.3) and the long-wavelength kinetic-Alfvén wave instability (§ 3.3.4) – and two electron-shear-driven ones – the electron-scale-transition (EST) instability (§ 4.4.8) and the whisper instability (§ 4.4.10) – at electron-Larmor and sub-electron-Larmor scales, respectively. Of these microinstabilities, the whisper instability seems to be of particular significance: it has an extremely large growth rate in certain parameter regimes, and is associated with a new high-![]() $\beta$ wave in a Maxwellian plasma, which also appears to have previously escaped attention. For convenience, a complete index of microinstabilities discussed in this paper is given in table 1, while the peak growth rates of these microinstabilities and the scales at which they occur (for a hydrogen CE plasma) are given in table 2. There do exist microinstabilities in CE plasma that are not represented in tables 1 and 2; however, we claim that the instabilities discussed in this paper are the most significant, on account of their large growth rates and/or low
$\beta$ wave in a Maxwellian plasma, which also appears to have previously escaped attention. For convenience, a complete index of microinstabilities discussed in this paper is given in table 1, while the peak growth rates of these microinstabilities and the scales at which they occur (for a hydrogen CE plasma) are given in table 2. There do exist microinstabilities in CE plasma that are not represented in tables 1 and 2; however, we claim that the instabilities discussed in this paper are the most significant, on account of their large growth rates and/or low ![]() $\beta$-stabilisation thresholds compared with the unrepresented ones.
$\beta$-stabilisation thresholds compared with the unrepresented ones.
Table 1. Index of microinstabilities. The microinstabilities listed here are those discussed in the main text, with the relevant sections indicated. We also indicate whether these microinstabilities are driven by macroscopic electron-/ion-temperature gradients associated with the CE distribution function, or by macroscopic electron/ion velocity gradients (shears): see § 2.2.1 for a discussion of this classification. Newly identified microinstabilities are indicated with an asterisk.

Table 2. Properties of microinstabilities. Typical wavenumbers and maximum growth rates of microinstabilities in strongly magnetised hydrogen CE plasma, and their ![]() $\beta$-stabilisation thresholds. Here,
$\beta$-stabilisation thresholds. Here, ![]() $\mu _e = m_e/m_i$. We assume scalings (2.55) to relate the magnitude of CE temperature-gradient-driven and CE shear-driven microinstabilities. These scalings lead to the non-Maxwellian component of the ion distribution function having magnitude
$\mu _e = m_e/m_i$. We assume scalings (2.55) to relate the magnitude of CE temperature-gradient-driven and CE shear-driven microinstabilities. These scalings lead to the non-Maxwellian component of the ion distribution function having magnitude ![]() ${\sim }\epsilon = {Ma} \, \lambda /L_V$, where
${\sim }\epsilon = {Ma} \, \lambda /L_V$, where ![]() $\lambda = \lambda _e = \lambda _i$,
$\lambda = \lambda _e = \lambda _i$, ![]() $L_V$ is the length scale of the CE plasma's bulk fluid motions in the direction parallel to the guide magnetic field (see (2.13d)) and
$L_V$ is the length scale of the CE plasma's bulk fluid motions in the direction parallel to the guide magnetic field (see (2.13d)) and ![]() ${Ma}$ is the Mach number of those bulk motions. The quoted wavenumbers and growth rates apply when the
${Ma}$ is the Mach number of those bulk motions. The quoted wavenumbers and growth rates apply when the ![]() $\beta$-stabilisation threshold is exceeded by an order-unity or much larger factor.
$\beta$-stabilisation threshold is exceeded by an order-unity or much larger factor.

Having systematically identified all significant microinstabilities, we can construct ‘stability maps’ of strongly magnetised CE plasma using ‘phase diagrams’ over a two-dimensional (![]() $\lambda /L$,
$\lambda /L$, ![]() $d_e/L$) parameter space at a fixed
$d_e/L$) parameter space at a fixed ![]() $\beta$. An example of such a map (for a hydrogen plasma with equal ion and electron temperatures) is shown in figure 1. The entire region of the (
$\beta$. An example of such a map (for a hydrogen plasma with equal ion and electron temperatures) is shown in figure 1. The entire region of the (![]() $\lambda /L, d_e/L$) space depicted in figure 1 could naively be characterised as pertaining to classical, collisional plasma, and thus describable by fluid equations, with transport coefficients given by standard CE theory. However, there is a significant region of the parameter space (which is demarcated by boundaries corresponding to the
$\lambda /L, d_e/L$) space depicted in figure 1 could naively be characterised as pertaining to classical, collisional plasma, and thus describable by fluid equations, with transport coefficients given by standard CE theory. However, there is a significant region of the parameter space (which is demarcated by boundaries corresponding to the ![]() $\beta$-stabilisation and collisional-stabilisation conditions) that is unstable to microinstabilities. In fact, in strongly magnetised plasma, the collisional-stabilisation condition is never satisfied, because there exist microinstabilities whose characteristic length scales are the ion- and electron-Larmor radii, respectively; this being the case, only the
$\beta$-stabilisation and collisional-stabilisation conditions) that is unstable to microinstabilities. In fact, in strongly magnetised plasma, the collisional-stabilisation condition is never satisfied, because there exist microinstabilities whose characteristic length scales are the ion- and electron-Larmor radii, respectively; this being the case, only the ![]() $\beta$-stabilisation condition guarantees kinetic stability.
$\beta$-stabilisation condition guarantees kinetic stability.

Figure 1. Stability map for the CE distribution function. Idealised illustration of the stability of strongly magnetised, classical, collisional hydrogen plasma to microinstabilities for different (non-dimensionalised) values of the mean free path ![]() $\lambda = \lambda _e = \lambda _i$ and the electron inertial scale
$\lambda = \lambda _e = \lambda _i$ and the electron inertial scale ![]() $d_e$. Here, the length scale
$d_e$. Here, the length scale ![]() $L_V$ to which
$L_V$ to which ![]() $\lambda$ and
$\lambda$ and ![]() $d_e$ are normalised is the length scale of the CE plasma's bulk fluid motions in the direction parallel to the guide magnetic field (see (2.13d)); we assume scalings (2.55) to relate the magnitude of CE temperature-gradient-driven and CE shear-driven microinstabilities, so the CE expansion parameter is
$d_e$ are normalised is the length scale of the CE plasma's bulk fluid motions in the direction parallel to the guide magnetic field (see (2.13d)); we assume scalings (2.55) to relate the magnitude of CE temperature-gradient-driven and CE shear-driven microinstabilities, so the CE expansion parameter is ![]() $\epsilon = {Ma} \, \lambda /L_V$ (see the caption of table 2 for definitions). The white region of the (
$\epsilon = {Ma} \, \lambda /L_V$ (see the caption of table 2 for definitions). The white region of the (![]() $d_e/L_V,{Ma} \, \lambda /L_V$) stability map is stable; the coloured regions are not. In the unstable regions, the fastest-growing microinstability is indicated by colour according to the figure's legend; in the regions where multiple microinstabilities could be operating simulataneously, multiple colours have been employed. The plasma beta
$d_e/L_V,{Ma} \, \lambda /L_V$) stability map is stable; the coloured regions are not. In the unstable regions, the fastest-growing microinstability is indicated by colour according to the figure's legend; in the regions where multiple microinstabilities could be operating simulataneously, multiple colours have been employed. The plasma beta ![]() $\beta$ here was taken to be
$\beta$ here was taken to be ![]() $\beta = 10^{4}$, and the Mach number
$\beta = 10^{4}$, and the Mach number ![]() ${Ma} = 1$.
${Ma} = 1$.
The effect of microinstabilities being present in CE plasma would be to change the non-Maxwellian components of the distribution function, and therefore to alter the CE-prescribed resistivity, thermal conductivity and/or viscosity. Identifying the dominant microinstability or microinstabilities in such plasmas (as is done in figure 1 for a hydrogen plasma) is then necessary for calculating the true transport coefficients, which are likely determined by the effective collisionality associated with the saturated state of the dominant microinstability rather than by Coulomb collisions. Although such calculations are not undertaken in this paper, it seems possible that the modified transport coefficients could be determined self-consistently in terms of macroscopic plasma properties such as temperature gradients or velocity shears. We note that the calculation presented here assumes that the CE distribution function is determined without the microinstabilities and thus is only correct when the plasma is stable. Therefore, strictly speaking, the only conclusion one can make when the CE plasma is unstable is that the naive CE values of transport coefficients should not be taken as correct.
We emphasise that kinetic instability of CE plasmas is a phenomenon of practical importance as well as academic interest. We illustrate this in tables 3 and 4, where the possibility of microinstabilities is considered for a selection of physical systems composed of classical, collisional plasma. We find that, while there exist some systems where CE plasmas are immune to microinstabilities – for example, the photosphere and chromosphere – there are many other astrophysical plasma systems that are likely susceptible to them. Similar considerations apply to a range of laser plasmas, including plasmas generated in inertial-confinement-fusion and laboratory-astrophysics experiments. Indeed, a recent experiment carried out on the National Ignition Facility (NIF) – part of a wider programme of work exploring magnetic-field amplification in turbulent laser plasmas (Tzeferacos et al. Reference Tzeferacos2018; Bott et al. Reference Bott2021c,Reference Bottb, Reference Bott2022) – found evidence for the existence of large-amplitude local temperature fluctuations over a range of scales, a finding that was inconsistent with Spitzer thermal conduction (Meinecke et al. Reference Meinecke2022). This claim was corroborated by magnetohydrodynamic (MHD) simulations (with the code FLASH) of the experiment that modelled thermal conduction either using the Spitzer model, or no explicit thermal conduction model: the latter simulations were found to be much closer to the actual experimental data. Because the plasma created in the NIF experiment is also anticipated by our theory to be susceptible to CE microinstabilities, observations of a discrepancy with CE-derived transport coefficients are tantalising. We note that the idea of microinstabilities emerging in both collisional astrophysical plasmas and laser plasmas is not a new one: see, e.g. Schekochihin et al. (Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005) or Hellinger & Trávníček (Reference Hellinger and Trávníček2015) in the former context; in the latter, Epperlein & Bell (Reference Epperlein and Bell1987) or Bell et al. (Reference Bell, Kingham, Watkins and Matthews2020). However, to our knowledge there does not exist a systematic treatment of the general kinetic stability of CE plasmas. This is the gap that this paper attempts to fill.
Table 3. Plasma parameters for some physical systems composed of classical, collisional plasma. The values of temperature and density of the WIGM given here are from Nicastro, Mathur & Elvis (Reference Nicastro, Mathur and Elvis2008), while those of the ICM come from Fabian (Reference Fabian1994). The estimates of the typical magnetic-field strengths and scale lengths for both the WIGM and the ICM are from Ryu et al. (Reference Ryu, Kang, Cho and Das2008). For simplicity, we have assumed equal ion and electron temperatures; however, we acknowledge that there is some uncertainty as to the validity of this assumption (see, e.g. Yoshida, Furlanetto & Hernquist Reference Yoshida, Furlanetto and Hernquist2005). Barkana & Loeb (Reference Barkana and Loeb2001) is the source of estimates for the IGM post reionisation. Estimates for typical solar parameters are from Wiegelmann, Thalmann & Solanki (Reference Wiegelmann, Thalmann and Solanki2014) and Stix (Reference Stix2012). The values of the temperature, electron density and scale length for ICF hot spots are from Abu-Shawareb (Reference Abu-Shawareb2022), who reported the first DT experiments carried out on the NIF to exceed the Lawson criterion for ignition; the estimates of the magnetic-field strength come from numerical simulations of a burning ICF hot spot with a similar fusion energy yield (Sadler et al. Reference Sadler, Walsh, Zhou and Li2022). The parameters for the laser-ablated carbon-hydrogen plasma are from an experiment on the OMEGA laser facility, with a 1 ns, 500 J pulse with a ![]() $0.351 \ {\rm \mu} \mathrm {m}$ wavelength (Li et al. Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Landen, Knauer and Smalyuk2007); we assume that the measured fields are found in front of the critical-density surface when estimating the density. The ‘TDYNO’ laser plasma is a turbulent carbon-hydrogen plasma that was produced as part of a recent laboratory astrophysics experiment on the NIF which found evidence of suppressed heat conduction (Meinecke et al. Reference Meinecke2022). Naturally, the systems described here often support a range of density, temperatures and magnetic fields, so the values provided should be understood as representative, but negotiable.
$0.351 \ {\rm \mu} \mathrm {m}$ wavelength (Li et al. Reference Li, Séguin, Frenje, Rygg, Petrasso, Town, Landen, Knauer and Smalyuk2007); we assume that the measured fields are found in front of the critical-density surface when estimating the density. The ‘TDYNO’ laser plasma is a turbulent carbon-hydrogen plasma that was produced as part of a recent laboratory astrophysics experiment on the NIF which found evidence of suppressed heat conduction (Meinecke et al. Reference Meinecke2022). Naturally, the systems described here often support a range of density, temperatures and magnetic fields, so the values provided should be understood as representative, but negotiable.

Table 4. Derived plasma parameters for systems composed of classical, collisional plasma. All parameters are calculated using Huba (Reference Huba1994), except for ![]() $k_{\mathrm {peak}} \lambda _e$. This is calculated by considering all possible instabilities, and then finding the magnitude of
$k_{\mathrm {peak}} \lambda _e$. This is calculated by considering all possible instabilities, and then finding the magnitude of ![]() $k_{\mathrm {peak}} \lambda _e$ for the fastest-growing instability satisfying
$k_{\mathrm {peak}} \lambda _e$ for the fastest-growing instability satisfying ![]() $k_{\mathrm {peak}} \lambda _e \gtrsim 1$. Depending on the values of other parameters, the fastest-growing instability varies between systems; in the WIGM, ICM, ICF, laser-ablation and TDYNO plasmas, the whistler heat-flux instability is the fastest-growing one, while in the reionised IGM, the transverse instability is. Formulae for
$k_{\mathrm {peak}} \lambda _e \gtrsim 1$. Depending on the values of other parameters, the fastest-growing instability varies between systems; in the WIGM, ICM, ICF, laser-ablation and TDYNO plasmas, the whistler heat-flux instability is the fastest-growing one, while in the reionised IGM, the transverse instability is. Formulae for ![]() $\lambda _e$ and
$\lambda _e$ and ![]() $\lambda _i$ are also given by (2.14a,b).
$\lambda _i$ are also given by (2.14a,b).

This paper has the following structure. In § 2, we discuss kinetic and fluid descriptions of classical plasma. We then describe the CE expansion in collisional plasma: we work out the CE distribution function arising in a two-species strongly magnetised plasma, evaluate the friction forces, heat and momentum fluxes necessary to construct a closed set of plasma-fluid equations and systematically estimate the size of the non-Maxwellian components of this distribution. Next, we discuss qualitatively the existence and nature of microinstabilities potentially arising in CE plasma, before presenting the methodology that we later use to perform the full linear, kinetic stability calculation. We provide an overview of this methodology in § 2.4, and then a much more detailed exposition of it in § 2.5: in particular, we describe in the latter how a simple form of the dispersion relation for the fastest microinstabilities can be obtained by considering the low-frequency limit ![]() $\gamma \ll k v_{\mathrm {th}s}$ of the hot-plasma dispersion relation, and how this simplified dispersion relation can be solved analytically. Readers who are uninterested in the technical details of this calculation are encouraged to pass over § 2.5; knowledge of its contents is not a pre-requisite for subsequent sections. In §§ 3 and 4, we construct stability maps (analogous to figure 1) showing the parameter ranges in which the CE distribution function is stable, to CET and CES microinstabilities, respectively. The parameters are
$\gamma \ll k v_{\mathrm {th}s}$ of the hot-plasma dispersion relation, and how this simplified dispersion relation can be solved analytically. Readers who are uninterested in the technical details of this calculation are encouraged to pass over § 2.5; knowledge of its contents is not a pre-requisite for subsequent sections. In §§ 3 and 4, we construct stability maps (analogous to figure 1) showing the parameter ranges in which the CE distribution function is stable, to CET and CES microinstabilities, respectively. The parameters are ![]() $\beta$ and
$\beta$ and ![]() $\lambda /L$, and we construct separate stability maps for CET and CES microinstabilities in order to take into account the fact that
$\lambda /L$, and we construct separate stability maps for CET and CES microinstabilities in order to take into account the fact that ![]() $L$ is in general not the same in the situations where these two types of microinstabilities occur. In § 3, we also discuss the significant CET microinstabilities that can occur (or not) at different values
$L$ is in general not the same in the situations where these two types of microinstabilities occur. In § 3, we also discuss the significant CET microinstabilities that can occur (or not) at different values ![]() $\lambda /L$ and
$\lambda /L$ and ![]() $\beta$, and provide simple analytic characterisations of them; in § 4, we do the same for significant CES microinstabilities. Finally, in § 5, we discuss the general implications of these instabilities for classical, collisional plasmas, and consider future research directions. Throughout this paper, most lengthy calculations are exiled to appendices; a glossary of mathematical notation is given in Appendix A.
$\beta$, and provide simple analytic characterisations of them; in § 4, we do the same for significant CES microinstabilities. Finally, in § 5, we discuss the general implications of these instabilities for classical, collisional plasmas, and consider future research directions. Throughout this paper, most lengthy calculations are exiled to appendices; a glossary of mathematical notation is given in Appendix A.
2. Problem set-up
2.1. Kinetic vs fluid description of classical plasma
The evolution of classical plasma is most generally described by kinetic theory, via the solution of Maxwell–Vlasov–Landau equations for the distribution functions of constituent particles. More specifically, in a kinetic description of a (non-relativistic) plasma, the distribution function ![]() $f_s(\boldsymbol {r},\boldsymbol {v},t)$ of the particle of species
$f_s(\boldsymbol {r},\boldsymbol {v},t)$ of the particle of species ![]() $s$ satisfies
$s$ satisfies
 \begin{equation} \frac{\partial f_{s}}{\partial t} + \boldsymbol{v} \boldsymbol{\cdot} \boldsymbol{\nabla} f_{s} + \frac{Z_s e}{m_s} \left(\boldsymbol{E}+ \frac{\boldsymbol{v} \times \boldsymbol{B}}{c}\right) \boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}}= \sum_{s'} \mathfrak{C}(f_s,f_{s'}) , \end{equation}
\begin{equation} \frac{\partial f_{s}}{\partial t} + \boldsymbol{v} \boldsymbol{\cdot} \boldsymbol{\nabla} f_{s} + \frac{Z_s e}{m_s} \left(\boldsymbol{E}+ \frac{\boldsymbol{v} \times \boldsymbol{B}}{c}\right) \boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}}= \sum_{s'} \mathfrak{C}(f_s,f_{s'}) , \end{equation}
where ![]() $t$ is time,
$t$ is time, ![]() $\boldsymbol {r}$ spatial position,
$\boldsymbol {r}$ spatial position, ![]() $\boldsymbol {v}$ the velocity,
$\boldsymbol {v}$ the velocity, ![]() $e$ the elementary charge,
$e$ the elementary charge, ![]() $Z_s e$ the charge and
$Z_s e$ the charge and ![]() $m_s$ the mass of species
$m_s$ the mass of species ![]() $s$,
$s$, ![]() $\boldsymbol {E}$ the electric field,
$\boldsymbol {E}$ the electric field, ![]() $\boldsymbol {B}$ the magnetic field,
$\boldsymbol {B}$ the magnetic field, ![]() $c$ the speed of light and
$c$ the speed of light and ![]() $\mathfrak {C}(f_s,f_{s'})$ the collision operator for interactions between species
$\mathfrak {C}(f_s,f_{s'})$ the collision operator for interactions between species ![]() $s$ and
$s$ and ![]() $s'$. Here, we do not yet give a specific form for
$s'$. Here, we do not yet give a specific form for ![]() $\mathfrak {C}(f_s,f_{s'})$; in general, an appropriate choice is the full Landau collision operator (Helander & Sigmar Reference Helander and Sigmar2005), but to aid tractability of some calculations that we carry out subsequently (see § 2.4.2), we will in some instances adopt simpler models such as the Krook operator (Bhatnagar, Gross & Krook Reference Bhatnagar, Gross and Krook1954). Equation (2.1) is coupled to Maxwell's equations:
$\mathfrak {C}(f_s,f_{s'})$; in general, an appropriate choice is the full Landau collision operator (Helander & Sigmar Reference Helander and Sigmar2005), but to aid tractability of some calculations that we carry out subsequently (see § 2.4.2), we will in some instances adopt simpler models such as the Krook operator (Bhatnagar, Gross & Krook Reference Bhatnagar, Gross and Krook1954). Equation (2.1) is coupled to Maxwell's equations:
Together, (2.1) and (2.2) form a closed set of governing equations.
The density ![]() $n_s$, bulk fluid velocity
$n_s$, bulk fluid velocity ![]() $\boldsymbol {V}_{s}$ and temperature
$\boldsymbol {V}_{s}$ and temperature ![]() $T_s$ of species
$T_s$ of species ![]() $s$ can be formally defined in terms of moments of the distribution function:
$s$ can be formally defined in terms of moments of the distribution function:
Governing ‘fluid’ equations are then derived by integrating (2.1) or outer products of (2.1) and the velocity variable ![]() $\boldsymbol {v}$ with respect to
$\boldsymbol {v}$ with respect to ![]() $\boldsymbol {v}$:
$\boldsymbol {v}$:
where
is the convective derivative with respect to the fluid motions of species ![]() $s$,
$s$, ![]() $p_s$ the pressure,
$p_s$ the pressure, ![]() $\boldsymbol {{\rm \pi} }_s$ the viscosity tensor and
$\boldsymbol {{\rm \pi} }_s$ the viscosity tensor and ![]() $\boldsymbol {q}_s$ the heat flux of species
$\boldsymbol {q}_s$ the heat flux of species ![]() $s$,
$s$, ![]() $\boldsymbol {R}_s$ the friction force on this species due to collisional interactions with other species, and
$\boldsymbol {R}_s$ the friction force on this species due to collisional interactions with other species, and ![]() $\mathcal {Q}_s$ the heating rate due to inter-species collisions. The latter quantities are formally defined in terms of the distribution function as follows:
$\mathcal {Q}_s$ the heating rate due to inter-species collisions. The latter quantities are formally defined in terms of the distribution function as follows:
The distribution function only appears in Maxwell's equations via its zeroth and first moments; namely, Gauss’ law (2.2a) and the Maxwell–Ampère law (2.2d) can be written as
Unlike the kinetic description, the fluid equations (2.4) combined with Maxwell's equations (2.2b), (2.2d), (2.7a) and (2.7b) are not a closed system: knowledge of the distribution function, not just of ![]() $n_s$,
$n_s$, ![]() $\boldsymbol {V}_s$ or
$\boldsymbol {V}_s$ or ![]() $T_s$, is required to calculate momentum and heat fluxes, as well as the friction force or heating.
$T_s$, is required to calculate momentum and heat fluxes, as well as the friction force or heating.
As discussed in the Introduction, solving fluid equations as opposed to kinetic equations is advantageous in many cases of interest. Since the dimensionality of the kinetic system is greater (a six-dimensional phase space vs three-dimensional position space), solving the kinetic system introduces both significant numerical and conceptual complexity. However, the system of fluid equations (2.4) is only usable if some type of closure can be introduced to calculate ![]() $\boldsymbol {{\rm \pi} }_s$,
$\boldsymbol {{\rm \pi} }_s$, ![]() $\boldsymbol {q}_{s}$,
$\boldsymbol {q}_{s}$, ![]() $\boldsymbol {R}_s$ and
$\boldsymbol {R}_s$ and ![]() $\mathcal {Q}_s$ in terms of
$\mathcal {Q}_s$ in terms of ![]() $n_s$,
$n_s$, ![]() $\boldsymbol {V}_s$ and
$\boldsymbol {V}_s$ and ![]() $T_s$. For classical plasmas, such a closure is generally not possible, except in the case of strongly collisional plasmas.
$T_s$. For classical plasmas, such a closure is generally not possible, except in the case of strongly collisional plasmas.
2.2. The Chapman–Enskog expansion
2.2.1. The CE distribution functions
For a classical, collisional plasma – i.e. a plasma where the mean free path ![]() $\lambda _s$ of particles of species
$\lambda _s$ of particles of species ![]() $s$ satisfies
$s$ satisfies ![]() $\lambda _s/L \ll 1$ for all
$\lambda _s/L \ll 1$ for all ![]() $s$,
$s$, ![]() $L$ being the length scale over which the macroscopic properties of the plasma vary – a formal procedure exists for deriving a closed system of fluid equations from a kinetic description of the plasma. This procedure is the CE expansion, which gives distribution functions that are close to, but not exactly, Maxwellian. We call them CE distribution functions. The non-Maxwellian components of the CE distribution functions of particle species
$L$ being the length scale over which the macroscopic properties of the plasma vary – a formal procedure exists for deriving a closed system of fluid equations from a kinetic description of the plasma. This procedure is the CE expansion, which gives distribution functions that are close to, but not exactly, Maxwellian. We call them CE distribution functions. The non-Maxwellian components of the CE distribution functions of particle species ![]() $s$ are proportional to
$s$ are proportional to ![]() $\lambda _s/L$, and must be present in order to support gradients of
$\lambda _s/L$, and must be present in order to support gradients of ![]() $n_s$,
$n_s$, ![]() $\boldsymbol {V}_s$ and
$\boldsymbol {V}_s$ and ![]() $T_s$ on
$T_s$ on ![]() ${O}(L)$ length scales, because (2.6b–e) are all zero for a Maxwellian plasma.
${O}(L)$ length scales, because (2.6b–e) are all zero for a Maxwellian plasma.
We consider a collisional electron–ion plasma (in which, by definition, ![]() $\mu _e \equiv m_e/m_i \ll 1$) with the property that all constituent particle species are strongly magnetised by the macroscopically varying magnetic field
$\mu _e \equiv m_e/m_i \ll 1$) with the property that all constituent particle species are strongly magnetised by the macroscopically varying magnetic field ![]() $\boldsymbol {B}$: that is, the Larmor radius
$\boldsymbol {B}$: that is, the Larmor radius ![]() $\rho _s \equiv m_s v_{\mathrm {th}s} c/|Z_s| e |\boldsymbol {B}|$ satisfies
$\rho _s \equiv m_s v_{\mathrm {th}s} c/|Z_s| e |\boldsymbol {B}|$ satisfies ![]() $\rho _s \ll \lambda _{s}$ both for the ions and for the electrons (here,
$\rho _s \ll \lambda _{s}$ both for the ions and for the electrons (here, ![]() $v_{\mathrm {th}s} \equiv \sqrt {2 T_s/m_s}$ is the thermal speed of species
$v_{\mathrm {th}s} \equiv \sqrt {2 T_s/m_s}$ is the thermal speed of species ![]() $s$). Equivalently, a strongly magnetised plasma is one in which the Larmor frequency
$s$). Equivalently, a strongly magnetised plasma is one in which the Larmor frequency ![]() $\varOmega _s \equiv e |Z_s|/m_s c$ satisfies
$\varOmega _s \equiv e |Z_s|/m_s c$ satisfies ![]() $\varOmega _s \tau _s \gg 1$, where
$\varOmega _s \tau _s \gg 1$, where ![]() $\tau _s$ is the collision time of species
$\tau _s$ is the collision time of species ![]() $s$. In such a plasma, the macroscopic variation of the fluid moments is locally anisotropic with respect to
$s$. In such a plasma, the macroscopic variation of the fluid moments is locally anisotropic with respect to ![]() $\boldsymbol {B}$;
$\boldsymbol {B}$; ![]() $L$ is the typical length scale of variation in the direction locally parallel to
$L$ is the typical length scale of variation in the direction locally parallel to ![]() $\boldsymbol {B}$. It can then be shown that, to first order of the CE expansion in
$\boldsymbol {B}$. It can then be shown that, to first order of the CE expansion in ![]() $\lambda _{s}/L \ll 1$, and to zeroth order in
$\lambda _{s}/L \ll 1$, and to zeroth order in ![]() $\rho _s/\lambda _{s} \ll 1$, the CE distribution functions of the electrons and ions are
$\rho _s/\lambda _{s} \ll 1$, the CE distribution functions of the electrons and ions are
 \begin{align} f_{e}(\tilde{v}_{e\|},\tilde{v}_{e\bot}) & = \frac{n_{e}}{v_{\mathrm{th}e}^3 {\rm \pi}^{3/2}} \exp \left(-\tilde{v}_{e}^2\right) \nonumber\\ &\quad \times \left\{1+\left[\eta_e^{T} A_e^T(\tilde{v}_e) + \eta_e^{R} A_e^R(\tilde{v}_e) + \eta_e^{u} A_e^u(\tilde{v}_e) \right] \tilde{v}_{e\|} + \epsilon_e C_e(\tilde{v}_e) \left(\tilde{v}_{e\|}^2- \frac{\tilde{v}_{e\bot}^2}{2}\right)\right\}, \end{align}
\begin{align} f_{e}(\tilde{v}_{e\|},\tilde{v}_{e\bot}) & = \frac{n_{e}}{v_{\mathrm{th}e}^3 {\rm \pi}^{3/2}} \exp \left(-\tilde{v}_{e}^2\right) \nonumber\\ &\quad \times \left\{1+\left[\eta_e^{T} A_e^T(\tilde{v}_e) + \eta_e^{R} A_e^R(\tilde{v}_e) + \eta_e^{u} A_e^u(\tilde{v}_e) \right] \tilde{v}_{e\|} + \epsilon_e C_e(\tilde{v}_e) \left(\tilde{v}_{e\|}^2- \frac{\tilde{v}_{e\bot}^2}{2}\right)\right\}, \end{align} \begin{align} f_{i}(\tilde{v}_{i\|},\tilde{v}_{i\bot}) & = \frac{n_{i}}{v_{\mathrm{th}i}^3 {\rm \pi}^{3/2}} \exp \left(-\tilde{v}_{i}^2\right) \nonumber\\ & \quad \times \left\{1+\eta_i A_i(\tilde{v}_i) \tilde{v}_{i\|} + \epsilon_i C_i(\tilde{v}_i) \left(\tilde{v}_{i\|}^2- \frac{\tilde{v}_{i\bot}^2}{2} \right)\right\} . \end{align}
\begin{align} f_{i}(\tilde{v}_{i\|},\tilde{v}_{i\bot}) & = \frac{n_{i}}{v_{\mathrm{th}i}^3 {\rm \pi}^{3/2}} \exp \left(-\tilde{v}_{i}^2\right) \nonumber\\ & \quad \times \left\{1+\eta_i A_i(\tilde{v}_i) \tilde{v}_{i\|} + \epsilon_i C_i(\tilde{v}_i) \left(\tilde{v}_{i\|}^2- \frac{\tilde{v}_{i\bot}^2}{2} \right)\right\} . \end{align}Let us define the various symbols employed in (2.8), before discussing the origin of these expressions and their significance for formulating fluid equations (see § 2.2.2).
The particle velocity ![]() $\boldsymbol {v}$ (with the corresponding speed
$\boldsymbol {v}$ (with the corresponding speed ![]() $v = |\boldsymbol {v}|$) is split into components parallel and perpendicular to the macroscopic magnetic field
$v = |\boldsymbol {v}|$) is split into components parallel and perpendicular to the macroscopic magnetic field ![]() $\boldsymbol {B} = B \hat {\boldsymbol {z}}$ as
$\boldsymbol {B} = B \hat {\boldsymbol {z}}$ as ![]() $\boldsymbol {v} = v_{\|} \hat {\boldsymbol {z}} + \boldsymbol {v}_{\bot }$, and the perpendicular plane is in turn characterised by two vectors
$\boldsymbol {v} = v_{\|} \hat {\boldsymbol {z}} + \boldsymbol {v}_{\bot }$, and the perpendicular plane is in turn characterised by two vectors ![]() $\hat {\boldsymbol {x}}$ and
$\hat {\boldsymbol {x}}$ and ![]() $\hat {\boldsymbol {y}}$ chosen so that
$\hat {\boldsymbol {y}}$ chosen so that ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ is an orthonormal basis. The perpendicular velocity is related to these basis vectors by the gyrophase angle
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ is an orthonormal basis. The perpendicular velocity is related to these basis vectors by the gyrophase angle ![]() $\phi$:
$\phi$:
The non-dimensionalised peculiar velocity ![]() $\tilde {\boldsymbol {v}}_s$ in the rest frame of the ion fluid is defined by
$\tilde {\boldsymbol {v}}_s$ in the rest frame of the ion fluid is defined by ![]() $\tilde {\boldsymbol {v}}_s \equiv (\boldsymbol {v}-\boldsymbol {V}_i)/v_{\mathrm {th}s}$,
$\tilde {\boldsymbol {v}}_s \equiv (\boldsymbol {v}-\boldsymbol {V}_i)/v_{\mathrm {th}s}$, ![]() $\tilde {v}_s \equiv |\tilde {\boldsymbol {v}}_s|$,
$\tilde {v}_s \equiv |\tilde {\boldsymbol {v}}_s|$, ![]() $\tilde {v}_{s\|} \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \tilde {\boldsymbol {v}}_s$ and
$\tilde {v}_{s\|} \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \tilde {\boldsymbol {v}}_s$ and ![]() $\tilde {v}_{s\bot } \equiv |\tilde {\boldsymbol {v}}_s-\tilde {v}_{s\|} \hat {\boldsymbol {z}}|$. The number densities satisfy the quasi-neutrality condition
$\tilde {v}_{s\bot } \equiv |\tilde {\boldsymbol {v}}_s-\tilde {v}_{s\|} \hat {\boldsymbol {z}}|$. The number densities satisfy the quasi-neutrality condition
where we have utilised ![]() $Z_{e} = -1$. We emphasise that
$Z_{e} = -1$. We emphasise that ![]() $n_{s}$,
$n_{s}$, ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ and
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ and ![]() $v_{\mathrm {th}s}$ all vary over length scales
$v_{\mathrm {th}s}$ all vary over length scales ![]() $L$ in the plasma, but not on shorter scales (at least not in the direction locally parallel to
$L$ in the plasma, but not on shorter scales (at least not in the direction locally parallel to ![]() $\boldsymbol {B}$). The functions
$\boldsymbol {B}$). The functions ![]() $A_e^T(\tilde {v}_e)$,
$A_e^T(\tilde {v}_e)$, ![]() $A_e^R(\tilde {v}_e)$,
$A_e^R(\tilde {v}_e)$, ![]() $A_e^u(\tilde {v}_e)$,
$A_e^u(\tilde {v}_e)$, ![]() $C_e(\tilde {v}_e)$,
$C_e(\tilde {v}_e)$, ![]() $A_i(\tilde {v}_i)$ and
$A_i(\tilde {v}_i)$ and ![]() $C_i(\tilde {v}_i)$ are isotropic functions whose precise forms depend only on the collision operator assumed in the original kinetic equation. Their magnitude is
$C_i(\tilde {v}_i)$ are isotropic functions whose precise forms depend only on the collision operator assumed in the original kinetic equation. Their magnitude is ![]() ${O}(1)$ when
${O}(1)$ when ![]() $\tilde {v}_e \sim 1$ or
$\tilde {v}_e \sim 1$ or ![]() $\tilde {v}_i \sim 1$, for electrons and ions, respectively. Finally, the parameters
$\tilde {v}_i \sim 1$, for electrons and ions, respectively. Finally, the parameters ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$,
$\eta _e^u$, ![]() $\eta _i$,
$\eta _i$, ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$ are defined as follows:
$\epsilon _i$ are defined as follows:
where ![]() $\lambda _{e}$ is the electron mean free path,
$\lambda _{e}$ is the electron mean free path, ![]() $\lambda _{i}$ the ion mean free path,
$\lambda _{i}$ the ion mean free path, ![]() $\tau _e$ the electron collision time,
$\tau _e$ the electron collision time, ![]() $R_{e\|} \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \boldsymbol {R}_{e}$ the parallel electron-friction force,
$R_{e\|} \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \boldsymbol {R}_{e}$ the parallel electron-friction force, ![]() $\boldsymbol {u}_{ei} \equiv \boldsymbol {V}_e - \boldsymbol {V}_i$ the relative electron–ion velocity,
$\boldsymbol {u}_{ei} \equiv \boldsymbol {V}_e - \boldsymbol {V}_i$ the relative electron–ion velocity, ![]() $u_{ei\|} \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \boldsymbol {u}_{ei}$,
$u_{ei\|} \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \boldsymbol {u}_{ei}$,
the traceless rate-of-strain tensor of species ![]() $s$,
$s$, ![]() $V_e$ (
$V_e$ (![]() $V_i$) the bulk electron-(ion-)fluid speed and
$V_i$) the bulk electron-(ion-)fluid speed and
are, respectively, the electron and ion temperature and the electron- and ion-flow length scales parallel to the background magnetic field. The mean free paths are formally defined for a two-species plasma by
and the collision times ![]() $\tau _e$ and
$\tau _e$ and ![]() $\tau _i$ are given in terms of macroscopic plasma parameters by
$\tau _i$ are given in terms of macroscopic plasma parameters by
 $$\begin{gather} \tau_{e} \equiv \frac{3 m_e^{1/2} T_e^{3/2}}{4 \sqrt{2 {\rm \pi}} Z_i^2 e^4 n_i \log{\varLambda_{\mathrm{CL}}}} , \end{gather}$$
$$\begin{gather} \tau_{e} \equiv \frac{3 m_e^{1/2} T_e^{3/2}}{4 \sqrt{2 {\rm \pi}} Z_i^2 e^4 n_i \log{\varLambda_{\mathrm{CL}}}} , \end{gather}$$ $$\begin{gather}\tau_{i} \equiv \frac{3 m_i^{1/2} T_i^{3/2}}{4 \sqrt{2 {\rm \pi}} Z_i^4 e^4 n_i \log{\varLambda_{\mathrm{CL}}}} , \end{gather}$$
$$\begin{gather}\tau_{i} \equiv \frac{3 m_i^{1/2} T_i^{3/2}}{4 \sqrt{2 {\rm \pi}} Z_i^4 e^4 n_i \log{\varLambda_{\mathrm{CL}}}} , \end{gather}$$
where ![]() $\log {\varLambda _{\mathrm {CL}}}$ is the Coulomb logarithm (Braginskii Reference Braginskii1965).Footnote 1 In a collisional plasma,
$\log {\varLambda _{\mathrm {CL}}}$ is the Coulomb logarithm (Braginskii Reference Braginskii1965).Footnote 1 In a collisional plasma, ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$,
$\eta _e^u$, ![]() $\eta _i$,
$\eta _i$, ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$ are assumed small. We note that all these parameters can be either positive or negative, depending on the orientation of temperature and velocity gradients.
$\epsilon _i$ are assumed small. We note that all these parameters can be either positive or negative, depending on the orientation of temperature and velocity gradients.
It is clear from their definitions that each of the non-Maxwellian terms associated with the parameters ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$,
$\eta _e^u$, ![]() $\eta _i$,
$\eta _i$, ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$ is linked to a different macroscopic physical quantity. Thus,
$\epsilon _i$ is linked to a different macroscopic physical quantity. Thus, ![]() $\eta _e^T$ and
$\eta _e^T$ and ![]() $\eta _i$ are proportional to the electron- and ion-temperature gradients, respectively; we will therefore refer to the associated non-Maxwellian terms as the CE electron-temperature-gradient term and the CE ion-temperature-gradient term. We refer to the non-Maxwellian term proportional to
$\eta _i$ are proportional to the electron- and ion-temperature gradients, respectively; we will therefore refer to the associated non-Maxwellian terms as the CE electron-temperature-gradient term and the CE ion-temperature-gradient term. We refer to the non-Maxwellian term proportional to ![]() $\eta _e^R$ as the CE electron-friction term, to the non-Maxwellian term proportional to
$\eta _e^R$ as the CE electron-friction term, to the non-Maxwellian term proportional to ![]() $\eta _e^u$ as the CE electron–ion-drift term, and the non-Maxwellian terms proportional to
$\eta _e^u$ as the CE electron–ion-drift term, and the non-Maxwellian terms proportional to ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$ as the CE electron-shear term and the CE ion-shear term. The friction and electron–ion-drift terms appear in the electron CE distribution function but not the ion CE distribution function because of our choice to define all velocities in the ion-fluid rest frame. We note that, while macroscopic variation of both the electron and ion densities is a priori allowed in our plasma, the derivation of the CE distribution functions reveals that such variation does not directly give rise to a non-Maxwellian perturbation to the CE distribution function (see Appendix B.1).
$\epsilon _i$ as the CE electron-shear term and the CE ion-shear term. The friction and electron–ion-drift terms appear in the electron CE distribution function but not the ion CE distribution function because of our choice to define all velocities in the ion-fluid rest frame. We note that, while macroscopic variation of both the electron and ion densities is a priori allowed in our plasma, the derivation of the CE distribution functions reveals that such variation does not directly give rise to a non-Maxwellian perturbation to the CE distribution function (see Appendix B.1).
The derivation of the CE distribution functions (2.8) for a two-species strongly magnetised plasma undergoing sonic motions (that is, ![]() $V_i \sim v_{\mathrm {th}i}$) from the kinetic equation (2.1) was first completed by Braginskii (Reference Braginskii1965) for arbitrary values of
$V_i \sim v_{\mathrm {th}i}$) from the kinetic equation (2.1) was first completed by Braginskii (Reference Braginskii1965) for arbitrary values of ![]() $\rho _s/\lambda _{s}$. We do not reproduce the full derivation in the main text, but, for the reader's convenience, we provide a derivation of (2.8) in Appendix B.1. The gist of the full derivation is to assume that the distribution function is close to a Maxwellian, with parameters that only evolve on a slow time scale
$\rho _s/\lambda _{s}$. We do not reproduce the full derivation in the main text, but, for the reader's convenience, we provide a derivation of (2.8) in Appendix B.1. The gist of the full derivation is to assume that the distribution function is close to a Maxwellian, with parameters that only evolve on a slow time scale ![]() $t' \sim t L/\lambda _e \sim t L/\lambda _i \gg t$. The kinetic equation (2.1) is then expanded and solved order by order in
$t' \sim t L/\lambda _e \sim t L/\lambda _i \gg t$. The kinetic equation (2.1) is then expanded and solved order by order in ![]() $\lambda _e/L \sim \lambda _i/L \ll 1$, allowing for the calculation of the (small) non-Maxwellian components of the distribution function. The small parameters
$\lambda _e/L \sim \lambda _i/L \ll 1$, allowing for the calculation of the (small) non-Maxwellian components of the distribution function. The small parameters ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$,
$\eta _e^u$, ![]() $\eta _i$,
$\eta _i$, ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$, as well as the isotropic functions
$\epsilon _i$, as well as the isotropic functions ![]() $A_e^T(\tilde {v}_e)$,
$A_e^T(\tilde {v}_e)$, ![]() $A_e^R(\tilde {v}_e)$,
$A_e^R(\tilde {v}_e)$, ![]() $A_e^u(\tilde {v}_e)$,
$A_e^u(\tilde {v}_e)$, ![]() $C_e(\tilde {v}_e)$,
$C_e(\tilde {v}_e)$, ![]() $A_i(\tilde {v}_i)$ and
$A_i(\tilde {v}_i)$ and ![]() $C_i(\tilde {v}_i)$ emerge during this calculation. In Appendix B.2, we provide a simple illustration of how the isotropic functions are determined by the specific choice of collision operator; in Appendices B.2.1 and B.2.2, we calculate them explicitly for Krook and Lorentz collision operators, respectively. For the full Landau collision operator, the equivalent calculation is more complicated, but can be performed (for example) by expanding the isotropic functions in Sonine polynomials (see Helander & Sigmar Reference Helander and Sigmar2005).
$C_i(\tilde {v}_i)$ emerge during this calculation. In Appendix B.2, we provide a simple illustration of how the isotropic functions are determined by the specific choice of collision operator; in Appendices B.2.1 and B.2.2, we calculate them explicitly for Krook and Lorentz collision operators, respectively. For the full Landau collision operator, the equivalent calculation is more complicated, but can be performed (for example) by expanding the isotropic functions in Sonine polynomials (see Helander & Sigmar Reference Helander and Sigmar2005).
2.2.2. Closure of fluid equations (2.4)
Once the CE distribution function has been calculated, the desired fluid closure can be obtained by evaluating the heat fluxes, the friction forces, and the momentum fluxes (2.6) associated with the non-Maxwellian components of the CE distribution functions. These calculations were carried out in full for arbitrary values of ![]() $\rho _s/\lambda _{s}$ by Braginskii (Reference Braginskii1965).
$\rho _s/\lambda _{s}$ by Braginskii (Reference Braginskii1965).
We do not reproduce the full fluid closure relations here; instead, we illustrate how the non-Maxwellian terms in the CE distribution functions (2.8) give rise to the friction force and heat fluxes parallel to the macroscopic magnetic field, as well as to the viscosity tensor. In a strongly magnetised two-species plasma (where ![]() $\rho _s \ll \lambda _s$), parallel friction forces and heat fluxes are typically much larger than their perpendicular or diamagnetic counterparts.
$\rho _s \ll \lambda _s$), parallel friction forces and heat fluxes are typically much larger than their perpendicular or diamagnetic counterparts.
(i) Heat fluxes. Recalling (2.6c), the parallel heat flux
 $q_{s\|} \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \boldsymbol {q}_{s}$ associated with species
$q_{s\|} \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \boldsymbol {q}_{s}$ associated with species  $s$ is given by
(2.16)where
$s$ is given by
(2.16)where \begin{equation} q_{s\|} = \frac{1}{2} \int \mathrm{d}^3\boldsymbol{v}_s' \, m_s \left|\boldsymbol{v}_s'\right|^2 v_{s\|}' \, f_{s} , \end{equation}
\begin{equation} q_{s\|} = \frac{1}{2} \int \mathrm{d}^3\boldsymbol{v}_s' \, m_s \left|\boldsymbol{v}_s'\right|^2 v_{s\|}' \, f_{s} , \end{equation} $\boldsymbol {v}_s' \equiv \boldsymbol {v}-\boldsymbol {V}_s$. Noting that the electron distribution function (2.8a) is specified in the rest frame of the ions, not electrons, it is necessary first to calculate the electron distribution function in the electron rest frame before calculating the parallel electron heat flux. An expression for this quantity is given by (B18) in Appendix B.1 as part of our derivation of (2.8a):
(2.17)Now substituting (2.17) into (2.16) (with
$\boldsymbol {v}_s' \equiv \boldsymbol {v}-\boldsymbol {V}_s$. Noting that the electron distribution function (2.8a) is specified in the rest frame of the ions, not electrons, it is necessary first to calculate the electron distribution function in the electron rest frame before calculating the parallel electron heat flux. An expression for this quantity is given by (B18) in Appendix B.1 as part of our derivation of (2.8a):
(2.17)Now substituting (2.17) into (2.16) (with \begin{align} f_{e}(v_{e\|}',v_{e\bot}') & = \frac{n_{e}}{v_{\mathrm{th}e}^3 {\rm \pi}^{3/2}} \exp \left(-\frac{|\boldsymbol{v}_{e}'|^2}{v_{\mathrm{th}e}^2}\right) \nonumber\\ & \quad \times \left\{1 + \left[\eta_e^T A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) +\eta_e^R A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) + \eta_e^u \left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) -1 \right) \right] \frac{v_{e\|}'}{v_{\mathrm{th}e}} \right. \nonumber\\ & \quad \left.+ \,\epsilon_e C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\}. \end{align}
\begin{align} f_{e}(v_{e\|}',v_{e\bot}') & = \frac{n_{e}}{v_{\mathrm{th}e}^3 {\rm \pi}^{3/2}} \exp \left(-\frac{|\boldsymbol{v}_{e}'|^2}{v_{\mathrm{th}e}^2}\right) \nonumber\\ & \quad \times \left\{1 + \left[\eta_e^T A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) +\eta_e^R A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) + \eta_e^u \left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) -1 \right) \right] \frac{v_{e\|}'}{v_{\mathrm{th}e}} \right. \nonumber\\ & \quad \left.+ \,\epsilon_e C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\}. \end{align} $s = e$), we find that the parallel electron heat flux is
(2.18)where
$s = e$), we find that the parallel electron heat flux is
(2.18)where \begin{equation} q_{e\|} ={-} n_{e} T_e v_{\mathrm{th}e} \left[\mathcal{A}_e^T \eta_e^T + \mathcal{A}_e^R \eta_e^R + \left(\mathcal{A}_e^u - \tfrac{1}{2}\right) \eta_e^u\right], \end{equation}(2.19)The minus signs in the definitions of
\begin{equation} q_{e\|} ={-} n_{e} T_e v_{\mathrm{th}e} \left[\mathcal{A}_e^T \eta_e^T + \mathcal{A}_e^R \eta_e^R + \left(\mathcal{A}_e^u - \tfrac{1}{2}\right) \eta_e^u\right], \end{equation}(2.19)The minus signs in the definitions of \begin{equation} \mathcal{A}_e^{T,R,u} ={-}\frac{4}{3\sqrt{\rm \pi}} \int_0^{\infty} \mathrm{d}\tilde{v}_e \, \tilde{v}_e^6 A_e^{T,R,u}(\tilde{v}_e) \exp \left(-\tilde{v}_e^2\right) . \end{equation}
\begin{equation} \mathcal{A}_e^{T,R,u} ={-}\frac{4}{3\sqrt{\rm \pi}} \int_0^{\infty} \mathrm{d}\tilde{v}_e \, \tilde{v}_e^6 A_e^{T,R,u}(\tilde{v}_e) \exp \left(-\tilde{v}_e^2\right) . \end{equation} $\mathcal {A}_e^{T,R,u}$ have been introduced so that
$\mathcal {A}_e^{T,R,u}$ have been introduced so that  $\mathcal {A}_e^{T,R,u} \geqslant 0$ for a typical collision operator (determining that these constants are indeed positive for any given collision operator is non-trivial, but it is a simple exercise to show this for a Krook collision operator, using the expressions for
$\mathcal {A}_e^{T,R,u} \geqslant 0$ for a typical collision operator (determining that these constants are indeed positive for any given collision operator is non-trivial, but it is a simple exercise to show this for a Krook collision operator, using the expressions for  $A_e^T(\tilde {v}_e)$,
$A_e^T(\tilde {v}_e)$,  $A_e^R(\tilde {v}_e)$ and
$A_e^R(\tilde {v}_e)$ and  $A_e^u(\tilde {v}_e)$ given in Appendix B.2.1). Expression (2.18) for the electron heat flux can be rewritten as
(2.20)where the parallel electron heat conductivity is defined by
$A_e^u(\tilde {v}_e)$ given in Appendix B.2.1). Expression (2.18) for the electron heat flux can be rewritten as
(2.20)where the parallel electron heat conductivity is defined by \begin{equation} q_{e\|} ={-} \kappa_{e}^{\|} \boldsymbol{\nabla}_{\|} T_e - \left[ \mathcal{A}_e^u - \frac{1}{2} - \frac{ \mathcal{A}_e^R}{\tilde{\mathcal{A}}_e^R}\left(\tilde{\mathcal{A}}_e^u-\frac{1}{2}\right)\right] n_e T_e u_{ei\|} , \end{equation}(2.21)and
\begin{equation} q_{e\|} ={-} \kappa_{e}^{\|} \boldsymbol{\nabla}_{\|} T_e - \left[ \mathcal{A}_e^u - \frac{1}{2} - \frac{ \mathcal{A}_e^R}{\tilde{\mathcal{A}}_e^R}\left(\tilde{\mathcal{A}}_e^u-\frac{1}{2}\right)\right] n_e T_e u_{ei\|} , \end{equation}(2.21)and \begin{equation} \kappa_{e}^{\|} = 2 \left(\mathcal{A}_e^T - \frac{\mathcal{A}_e^R}{\tilde{\mathcal{A}}_e^R} \tilde{\mathcal{A}}_e^T\right) \frac{n_e T_e \tau_e}{m_e} , \end{equation}(2.22)Numerical evaluation of the coefficients
\begin{equation} \kappa_{e}^{\|} = 2 \left(\mathcal{A}_e^T - \frac{\mathcal{A}_e^R}{\tilde{\mathcal{A}}_e^R} \tilde{\mathcal{A}}_e^T\right) \frac{n_e T_e \tau_e}{m_e} , \end{equation}(2.22)Numerical evaluation of the coefficients \begin{equation} \tilde{\mathcal{A}}_e^{T,R,u} ={-}\frac{4}{3\sqrt{\rm \pi}} \int_0^{\infty} \mathrm{d}\tilde{v}_e \, \tilde{v}_e^4 A_e^{T,R,u}(\tilde{v}_e) \exp \left(-\tilde{v}_e^2\right) . \end{equation}
\begin{equation} \tilde{\mathcal{A}}_e^{T,R,u} ={-}\frac{4}{3\sqrt{\rm \pi}} \int_0^{\infty} \mathrm{d}\tilde{v}_e \, \tilde{v}_e^4 A_e^{T,R,u}(\tilde{v}_e) \exp \left(-\tilde{v}_e^2\right) . \end{equation} $\mathcal {A}_e^{T,R,u}$ and
$\mathcal {A}_e^{T,R,u}$ and  $\tilde {\mathcal {A}}_e^{T,R,u}$ for the Landau collision operator gives (Braginskii Reference Braginskii1965)
(2.23)
$\tilde {\mathcal {A}}_e^{T,R,u}$ for the Landau collision operator gives (Braginskii Reference Braginskii1965)
(2.23) \begin{equation} q_{e\|} \simeq{-} 3.16 \frac{n_e T_e \tau_e}{m_e} \boldsymbol{\nabla}_{\|} T_e + 0.71 n_e T_e u_{ei\|} . \end{equation}
\begin{equation} q_{e\|} \simeq{-} 3.16 \frac{n_e T_e \tau_e}{m_e} \boldsymbol{\nabla}_{\|} T_e + 0.71 n_e T_e u_{ei\|} . \end{equation}The ion heat flux can be calculated directly from (2.16) (
 $s = i$) using (2.8b):
(2.24)where
$s = i$) using (2.8b):
(2.24)where \begin{equation} q_{i\|} ={-} n_{i} T_i v_{\mathrm{th}i} \mathcal{A}_i \eta_i , \end{equation}(2.25)This becomes
\begin{equation} q_{i\|} ={-} n_{i} T_i v_{\mathrm{th}i} \mathcal{A}_i \eta_i , \end{equation}(2.25)This becomes \begin{equation} \mathcal{A}_i ={-}\frac{4}{3\sqrt{\rm \pi}} \int_0^{\infty} \mathrm{d}\tilde{v}_i \, \tilde{v}_i^6 A_i(\tilde{v}_i) \exp \left(-\tilde{v}_i^2\right) . \end{equation}(2.26)where the parallel ion heat conductivity is
\begin{equation} \mathcal{A}_i ={-}\frac{4}{3\sqrt{\rm \pi}} \int_0^{\infty} \mathrm{d}\tilde{v}_i \, \tilde{v}_i^6 A_i(\tilde{v}_i) \exp \left(-\tilde{v}_i^2\right) . \end{equation}(2.26)where the parallel ion heat conductivity is \begin{equation} q_{i\|} ={-} \kappa_{i}^{\|} \boldsymbol{\nabla}_{\|} T_i , \end{equation}(2.27)The last equality is for the Landau collision operator (Braginskii Reference Braginskii1965). Note that the absence of a term proportional to the electron–ion-drift in the ion heat flux (2.24) is physically due to the smallness of the ion–electron collision operator (Helander & Sigmar Reference Helander and Sigmar2005).
\begin{equation} q_{i\|} ={-} \kappa_{i}^{\|} \boldsymbol{\nabla}_{\|} T_i , \end{equation}(2.27)The last equality is for the Landau collision operator (Braginskii Reference Braginskii1965). Note that the absence of a term proportional to the electron–ion-drift in the ion heat flux (2.24) is physically due to the smallness of the ion–electron collision operator (Helander & Sigmar Reference Helander and Sigmar2005). \begin{equation} \kappa_{i}^{\|} ={-}2 \mathcal{A}_i \frac{n_i T_i \tau_i}{m_i} \simeq{-} 3.9 \frac{n_i T_i \tau_i}{m_i} . \end{equation}
\begin{equation} \kappa_{i}^{\|} ={-}2 \mathcal{A}_i \frac{n_i T_i \tau_i}{m_i} \simeq{-} 3.9 \frac{n_i T_i \tau_i}{m_i} . \end{equation}(ii) Friction force. We evaluate the friction force by considering the electron–ion-drift associated with electron CE distribution function. Namely, noting that
(2.28)it follows from (2.8a) that \begin{equation} u_{ei\|} = \frac{v_{\mathrm{th}e}^4}{n_e} \int \mathrm{d}^3 \tilde{\boldsymbol{v}}_e \, \tilde{v}_{e\|} f_{e} , \end{equation}(2.29)This expression can in turn be used to relate the parallel electron-friction force
\begin{equation} u_{ei\|} = \frac{v_{\mathrm{th}e}^4}{n_e} \int \mathrm{d}^3 \tilde{\boldsymbol{v}}_e \, \tilde{v}_{e\|} f_{e} , \end{equation}(2.29)This expression can in turn be used to relate the parallel electron-friction force \begin{equation} u_{ei\|} = v_{\mathrm{th}e} \left(\tilde{\mathcal{A}}_e^T \eta_e^T + \tilde{\mathcal{A}}_e^R \eta_e^R + \tilde{\mathcal{A}}_e^u \eta_e^u \right) . \end{equation}
\begin{equation} u_{ei\|} = v_{\mathrm{th}e} \left(\tilde{\mathcal{A}}_e^T \eta_e^T + \tilde{\mathcal{A}}_e^R \eta_e^R + \tilde{\mathcal{A}}_e^u \eta_e^u \right) . \end{equation} $R_{e\|}$, defined in (2.6d), to electron flows and temperature gradients
(2.30)Evaluating the coefficients
$R_{e\|}$, defined in (2.6d), to electron flows and temperature gradients
(2.30)Evaluating the coefficients \begin{equation} R_{e\|} ={-}\left(\frac{2 \tilde{\mathcal{A}}_e^u + 1}{2 \tilde{\mathcal{A}}_e^R}\right) \frac{n_e m_e u_{ei\|}}{\tau_e} - \frac{\tilde{\mathcal{A}}_e^T}{\tilde{\mathcal{A}}_e^R} n_e \boldsymbol{\nabla}_{\|} T_e . \end{equation}
\begin{equation} R_{e\|} ={-}\left(\frac{2 \tilde{\mathcal{A}}_e^u + 1}{2 \tilde{\mathcal{A}}_e^R}\right) \frac{n_e m_e u_{ei\|}}{\tau_e} - \frac{\tilde{\mathcal{A}}_e^T}{\tilde{\mathcal{A}}_e^R} n_e \boldsymbol{\nabla}_{\|} T_e . \end{equation} $\tilde {\mathcal {A}}_e^T$,
$\tilde {\mathcal {A}}_e^T$,  $\tilde {\mathcal {A}}_e^R$ and
$\tilde {\mathcal {A}}_e^R$ and  $\tilde {\mathcal {A}}_e^u$ for the full Landau collision operator, one finds (Braginskii Reference Braginskii1965)
(2.31)
$\tilde {\mathcal {A}}_e^u$ for the full Landau collision operator, one finds (Braginskii Reference Braginskii1965)
(2.31) \begin{equation} R_{e\|} \simeq{-}0.51 \frac{n_e m_e u_{ei\|}}{\tau_e} - 0.71 n_e \boldsymbol{\nabla}_{\|} T_e . \end{equation}
\begin{equation} R_{e\|} \simeq{-}0.51 \frac{n_e m_e u_{ei\|}}{\tau_e} - 0.71 n_e \boldsymbol{\nabla}_{\|} T_e . \end{equation}(iii) Viscosity tensor. For gyrotropic distributions such as the CE distribution functions (2.8), the viscosity tensor
 $\boldsymbol {{\rm \pi} }_s$ of species
$\boldsymbol {{\rm \pi} }_s$ of species  $s$ defined by (2.6b) – which is the momentum flux excluding the convective terms and isotropic pressure – is given by
(2.32)where the parallel pressure
$s$ defined by (2.6b) – which is the momentum flux excluding the convective terms and isotropic pressure – is given by
(2.32)where the parallel pressure \begin{equation} \boldsymbol{\rm \pi}_s = \left(p_{s\|} - p_{s\perp}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}}-\tfrac{1}{3}\boldsymbol{\mathsf{I}}\right) , \end{equation}
\begin{equation} \boldsymbol{\rm \pi}_s = \left(p_{s\|} - p_{s\perp}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}}-\tfrac{1}{3}\boldsymbol{\mathsf{I}}\right) , \end{equation} $p_{s\|}$ and the perpendicular pressure
$p_{s\|}$ and the perpendicular pressure  $p_{s\bot }$ are defined by
(2.33a)
$p_{s\bot }$ are defined by
(2.33a) $$\begin{align} p_{s\|} &\equiv \int \mathrm{d}^3 \boldsymbol{v}_s' \, m_s |v_{s\|}'|^2 f_{s} = n_{s} T_{s} \left(1-\frac{2}{3}\epsilon_s \mathcal{C}_s\right) , \end{align}$$(2.33b)with the last expressions having been obtained on substitution of the CE distribution function (2.8), and
$$\begin{align} p_{s\|} &\equiv \int \mathrm{d}^3 \boldsymbol{v}_s' \, m_s |v_{s\|}'|^2 f_{s} = n_{s} T_{s} \left(1-\frac{2}{3}\epsilon_s \mathcal{C}_s\right) , \end{align}$$(2.33b)with the last expressions having been obtained on substitution of the CE distribution function (2.8), and $$\begin{align}p_{s\bot} &\equiv \frac{1}{2}\int \mathrm{d}^3 \boldsymbol{v}_{s}' \, m_s |\boldsymbol{v}_{s\bot}'|^2 f_{s} = n_{s} T_{s} \left(1+\frac{1}{3}\epsilon_s \mathcal{C}_s\right) , \end{align}$$(2.34)The sign of the constant
$$\begin{align}p_{s\bot} &\equiv \frac{1}{2}\int \mathrm{d}^3 \boldsymbol{v}_{s}' \, m_s |\boldsymbol{v}_{s\bot}'|^2 f_{s} = n_{s} T_{s} \left(1+\frac{1}{3}\epsilon_s \mathcal{C}_s\right) , \end{align}$$(2.34)The sign of the constant \begin{equation} \mathcal{C}_s ={-}\frac{8}{5\sqrt{\rm \pi}} \int_0^{\infty} \mathrm{d}\tilde{v}_s \, \tilde{v}_s^6 C_s(\tilde{v}_s) \exp \left(-\tilde{v}_s^2\right) . \end{equation}
\begin{equation} \mathcal{C}_s ={-}\frac{8}{5\sqrt{\rm \pi}} \int_0^{\infty} \mathrm{d}\tilde{v}_s \, \tilde{v}_s^6 C_s(\tilde{v}_s) \exp \left(-\tilde{v}_s^2\right) . \end{equation} $\mathcal {C}_s$ is again chosen so that
$\mathcal {C}_s$ is again chosen so that  $\mathcal {C}_s > 0$ for typical collision operators; for the Landau collision operator,
$\mathcal {C}_s > 0$ for typical collision operators; for the Landau collision operator,  $\mathcal {C}_e \simeq 1.1$ and
$\mathcal {C}_e \simeq 1.1$ and  $\mathcal {C}_i \simeq 1.44$ (Braginskii Reference Braginskii1965). We note for reference that the parameter
$\mathcal {C}_i \simeq 1.44$ (Braginskii Reference Braginskii1965). We note for reference that the parameter  $\epsilon _s$ (see (2.11e–f)) has a simple relationship to the pressure anisotropy of species
$\epsilon _s$ (see (2.11e–f)) has a simple relationship to the pressure anisotropy of species  $s$: utilising (2.33), one finds
(2.35)Using (2.33), the viscosity tensor (2.32) can be written
$s$: utilising (2.33), one finds
(2.35)Using (2.33), the viscosity tensor (2.32) can be written \begin{equation} \varDelta_s \equiv \frac{p_{s\bot}-p_{s\|}}{p_{s}} = \mathcal{C}_s \epsilon_s . \end{equation}(2.36)where the dynamic viscosity of species
\begin{equation} \varDelta_s \equiv \frac{p_{s\bot}-p_{s\|}}{p_{s}} = \mathcal{C}_s \epsilon_s . \end{equation}(2.36)where the dynamic viscosity of species \begin{equation} \boldsymbol{\rm \pi}_s ={-} \frac{\mu_{{v}s}}{2} \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) {\left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_s} , \end{equation}
\begin{equation} \boldsymbol{\rm \pi}_s ={-} \frac{\mu_{{v}s}}{2} \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) {\left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_s} , \end{equation} $s$ is
(2.37)
$s$ is
(2.37) \begin{equation} \mu_{{v}s} \equiv 2 \mathcal{C}_s n_s T_s \tau_s . \end{equation}
\begin{equation} \mu_{{v}s} \equiv 2 \mathcal{C}_s n_s T_s \tau_s . \end{equation}(iv) Thermal energy transfer between species. It can be shown that for the CE distribution functions (2.8), the rate of thermal energy transfer from electrons to ions
 $\mathcal {Q}_e$ is simply
(2.38)while the rate of thermal energy transfer from ions to electrons vanishes:
$\mathcal {Q}_e$ is simply
(2.38)while the rate of thermal energy transfer from ions to electrons vanishes: \begin{equation} \mathcal{Q}_e ={-} \boldsymbol{R}_e \boldsymbol{\cdot} \boldsymbol{u}_{ei} , \end{equation}
\begin{equation} \mathcal{Q}_e ={-} \boldsymbol{R}_e \boldsymbol{\cdot} \boldsymbol{u}_{ei} , \end{equation} $\mathcal {Q}_i \approx 0$. This is because the ion–electron collision rate is assumed small (by a factor of the mass ratio) compared with the ion–ion collision rate when deriving (2.8b), and is thus neglected. Braginskii (Reference Braginskii1965) shows that, in fact, there is a non-zero (but small) rate of transfer
(2.39)The time scale on which the ion and electron temperatures equilibrate is the ion–electron temperature equilibration time
$\mathcal {Q}_i \approx 0$. This is because the ion–electron collision rate is assumed small (by a factor of the mass ratio) compared with the ion–ion collision rate when deriving (2.8b), and is thus neglected. Braginskii (Reference Braginskii1965) shows that, in fact, there is a non-zero (but small) rate of transfer
(2.39)The time scale on which the ion and electron temperatures equilibrate is the ion–electron temperature equilibration time \begin{equation} \mathcal{Q}_i ={-}\mathcal{Q}_e - \boldsymbol{R}_e \boldsymbol{\cdot} \boldsymbol{u}_{ei} = \frac{3 n_e m_e}{m_i \tau_{e}} \left(T_e-T_i\right) . \end{equation}(2.40)
\begin{equation} \mathcal{Q}_i ={-}\mathcal{Q}_e - \boldsymbol{R}_e \boldsymbol{\cdot} \boldsymbol{u}_{ei} = \frac{3 n_e m_e}{m_i \tau_{e}} \left(T_e-T_i\right) . \end{equation}(2.40) \begin{equation} \tau_{ie}^{\rm eq} \equiv \tfrac{1}{2} \mu_e^{{-}1/2} \tau_{i} . \end{equation}
\begin{equation} \tau_{ie}^{\rm eq} \equiv \tfrac{1}{2} \mu_e^{{-}1/2} \tau_{i} . \end{equation}
In summary, the non-Maxwellian components of the CE distribution function are essential for a collisional plasma to be able to support fluxes of heat and momentum. More specifically, (2.20) demonstrates that the electron heat fluxes in a CE plasma are proportional to both temperature gradients and electron–ion drifts, and are carried by the electron-temperature-gradient, friction and electron–ion-drift terms of the CE distribution function. In contrast, the ion heat fluxes (2.26) are proportional only to ion temperature gradients (and carried by the CE ion-temperature-gradient term). Momentum fluxes (2.36) for electrons and ions are carried by the CE electron- and ion-shear terms, respectively, and are proportional to components of the rate-of-strain tensor.
2.2.3. Relative size of non-Maxwellian terms in the CE distribution function
In the case of magnetised, two-species plasma satisfying ![]() $T_i \sim T_e$, (2.11) can be used to estimate the size of the small parameters
$T_i \sim T_e$, (2.11) can be used to estimate the size of the small parameters ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$,
$\eta _e^u$, ![]() $\eta _i$,
$\eta _i$, ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$. Although these parameters are a priori proportional to
$\epsilon _i$. Although these parameters are a priori proportional to ![]() $\lambda _s/L$ for both ions and electrons, their precise magnitudes are, in fact, subtly different. Namely, the terms associated with
$\lambda _s/L$ for both ions and electrons, their precise magnitudes are, in fact, subtly different. Namely, the terms associated with ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$ and
$\eta _e^u$ and ![]() $\eta _i$ are gradients of the electron and ion temperatures and electron–ion relative parallel drift velocities, whereas terms associated with
$\eta _i$ are gradients of the electron and ion temperatures and electron–ion relative parallel drift velocities, whereas terms associated with ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$ involve gradients of the bulk flows (cf. (2.11)) – and these gradients do not necessarily occur on the same length scale. Recalling that the (electron) temperature and the (ion) flow length scales parallel to the macroscopic magnetic field are defined by (cf. (2.13))
$\epsilon _i$ involve gradients of the bulk flows (cf. (2.11)) – and these gradients do not necessarily occur on the same length scale. Recalling that the (electron) temperature and the (ion) flow length scales parallel to the macroscopic magnetic field are defined by (cf. (2.13))
where ![]() $\boldsymbol{\mathsf{W}}_i$ is the ion rate-of-strain tensor (2.12), and assuming that
$\boldsymbol{\mathsf{W}}_i$ is the ion rate-of-strain tensor (2.12), and assuming that ![]() $L_{T_i} = |\boldsymbol {\nabla }_{\|} \log T_i |^{-1} \sim L_{T}$ (an assumption we will check a posteriori), it follows from (2.11) that
$L_{T_i} = |\boldsymbol {\nabla }_{\|} \log T_i |^{-1} \sim L_{T}$ (an assumption we will check a posteriori), it follows from (2.11) that
where ![]() ${Ma} \equiv V_i/v_{\mathrm {th}i}$ is the Mach number. Note that, to arrive at (2.42b), we assumed that
${Ma} \equiv V_i/v_{\mathrm {th}i}$ is the Mach number. Note that, to arrive at (2.42b), we assumed that ![]() $R_{e\|} \sim p_e/L_{T}$ and
$R_{e\|} \sim p_e/L_{T}$ and ![]() $u_{ei\|} \sim v_{\mathrm {th}e} \lambda _e/L_T$, justified by (2.30) and (2.29), respectively. The relative magnitudes of
$u_{ei\|} \sim v_{\mathrm {th}e} \lambda _e/L_T$, justified by (2.30) and (2.29), respectively. The relative magnitudes of ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$,
$\eta _e^u$, ![]() $\eta _i$,
$\eta _i$, ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$ therefore depend on the Mach number of the plasma, as well as on the length scales
$\epsilon _i$ therefore depend on the Mach number of the plasma, as well as on the length scales ![]() $L_T$ and
$L_T$ and ![]() $L_V$.
$L_V$.
In the work of Braginskii (Reference Braginskii1965), who a priori presumes all ‘fluid’ quantities in the plasma to vary on just a single scale ![]() $L \sim L_T \sim L_V$, with sonic ordering
$L \sim L_T \sim L_V$, with sonic ordering ![]() ${Ma} \lesssim 1$, determining the relative size of these parameters for a hydrogen plasma (
${Ma} \lesssim 1$, determining the relative size of these parameters for a hydrogen plasma (![]() $Z_i = 1$) is simple:
$Z_i = 1$) is simple:
However, in most interesting applications, this single-scale ordering is incorrect. In a plasma with ![]() $\lambda _s/L \ll 1$ under Braginskii's ordering, motions on many scales naturally arise. The fluid Reynolds number in such a plasma is given by
$\lambda _s/L \ll 1$ under Braginskii's ordering, motions on many scales naturally arise. The fluid Reynolds number in such a plasma is given by
where ![]() $V_0$ is the typical fluid velocity at the scale
$V_0$ is the typical fluid velocity at the scale ![]() $L_0$ of driving motions and
$L_0$ of driving motions and ![]() $\nu \equiv \mu _{{v}i}/m_i n_i \sim v_{ \mathrm {th}i} \lambda _i$ is the kinematic viscosity (see (2.37)). Typically, this number is large:
$\nu \equiv \mu _{{v}i}/m_i n_i \sim v_{ \mathrm {th}i} \lambda _i$ is the kinematic viscosity (see (2.37)). Typically, this number is large:
where we have assumed ![]() ${Ma}_0 \equiv V_0/v_{\mathrm {th}i} \lesssim 1$, in line with Braginskii's sonic ordering. Therefore, such a plasma will naturally become turbulent and exhibit motions across a range of scales. As a consequence, velocity and temperature fluctuations on the smallest (fluid) scales must be considered, since the associated shears and temperature gradients are the largest. To estimate
${Ma}_0 \equiv V_0/v_{\mathrm {th}i} \lesssim 1$, in line with Braginskii's sonic ordering. Therefore, such a plasma will naturally become turbulent and exhibit motions across a range of scales. As a consequence, velocity and temperature fluctuations on the smallest (fluid) scales must be considered, since the associated shears and temperature gradients are the largest. To estimate ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$,
$\eta _e^u$, ![]() $\eta _i$,
$\eta _i$, ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$ accurately, we must determine the magnitude of these gradients.
$\epsilon _i$ accurately, we must determine the magnitude of these gradients.
First, let ![]() $\ell _{\nu }$ be the smallest scale on which the velocity varies due to turbulent motions (the Kolmogorov scale), with velocity fluctuations on scales
$\ell _{\nu }$ be the smallest scale on which the velocity varies due to turbulent motions (the Kolmogorov scale), with velocity fluctuations on scales ![]() $\ell \ll \ell _{\nu }$ being suppressed by viscous diffusion. Then it follows that
$\ell \ll \ell _{\nu }$ being suppressed by viscous diffusion. Then it follows that ![]() ${Re}_{\ell _{\nu }} \sim 1$, where
${Re}_{\ell _{\nu }} \sim 1$, where ![]() ${Re}_\ell \equiv V(\ell ) \ell /\nu$ is the scale-dependent Reynolds number and
${Re}_\ell \equiv V(\ell ) \ell /\nu$ is the scale-dependent Reynolds number and ![]() $V(\ell )$ is the typical fluid velocity on scale
$V(\ell )$ is the typical fluid velocity on scale ![]() $\ell$. For Kolmogorov turbulence,
$\ell$. For Kolmogorov turbulence,
 \begin{equation} \frac{V\!\left(\ell\right)}{V_0} \sim \left(\frac{\ell}{L_0}\right)^{1/3} \sim \left(\frac{{Re}_\ell}{Re} \right)^{1/4}, \end{equation}
\begin{equation} \frac{V\!\left(\ell\right)}{V_0} \sim \left(\frac{\ell}{L_0}\right)^{1/3} \sim \left(\frac{{Re}_\ell}{Re} \right)^{1/4}, \end{equation}
and ![]() $\ell /L_0 \sim ({{Re}_\ell }/{Re} )^{3/4}$, which gives
$\ell /L_0 \sim ({{Re}_\ell }/{Re} )^{3/4}$, which gives ![]() $V(\ell )/\ell \sim (V_0/L_0) ({{Re}_\ell }/{Re} )^{-1/2}$, and thus, from (2.45),
$V(\ell )/\ell \sim (V_0/L_0) ({{Re}_\ell }/{Re} )^{-1/2}$, and thus, from (2.45),
 \begin{equation} \frac{V\!\left(\ell_\nu\right)}{\ell_\nu} \sim \frac{V_0}{L_0} \left(\frac{{Re}_{\ell_\nu}}{Re} \right)^{{-}1/2} \sim {Ma}_0^{1/2} \left(\frac{\lambda_{i}}{L_0}\right)^{{-}1/2} \frac{V_0}{L_0} . \end{equation}
\begin{equation} \frac{V\!\left(\ell_\nu\right)}{\ell_\nu} \sim \frac{V_0}{L_0} \left(\frac{{Re}_{\ell_\nu}}{Re} \right)^{{-}1/2} \sim {Ma}_0^{1/2} \left(\frac{\lambda_{i}}{L_0}\right)^{{-}1/2} \frac{V_0}{L_0} . \end{equation}We therefore conclude that
 \begin{equation} L_V \sim \ell_{\nu} \frac{V_0}{V\!\left(\ell_\nu\right)} \sim L_0 {Ma}_0^{{-}1/2} \left(\frac{\lambda_{i}}{L_0}\right)^{1/2} . \end{equation}
\begin{equation} L_V \sim \ell_{\nu} \frac{V_0}{V\!\left(\ell_\nu\right)} \sim L_0 {Ma}_0^{{-}1/2} \left(\frac{\lambda_{i}}{L_0}\right)^{1/2} . \end{equation} Next, the smallest scale on which the electron temperature varies, ![]() $\ell _{\chi }$, is the scale below which temperature fluctuations are suppressed by thermal diffusion; it satisfies
$\ell _{\chi }$, is the scale below which temperature fluctuations are suppressed by thermal diffusion; it satisfies ![]() ${Pe}_{\ell _{\chi }} \sim 1$, where
${Pe}_{\ell _{\chi }} \sim 1$, where ![]() ${Pe}_\ell \equiv V(\ell ) \ell /\chi$ is the scale-dependent Péclet number and
${Pe}_\ell \equiv V(\ell ) \ell /\chi$ is the scale-dependent Péclet number and ![]() $\chi \equiv 2 \kappa _{e}^{\|}/3 n_e \sim v_{\mathrm {th}e} \lambda _{e}$ is the (parallel) thermal diffusivity (see (2.21)). Because temperature is passively advected by the flow, the temperature fluctuation
$\chi \equiv 2 \kappa _{e}^{\|}/3 n_e \sim v_{\mathrm {th}e} \lambda _{e}$ is the (parallel) thermal diffusivity (see (2.21)). Because temperature is passively advected by the flow, the temperature fluctuation ![]() $T(\ell )$ at any scale
$T(\ell )$ at any scale ![]() $\ell > \ell _\chi$ obeys the same scaling as the bulk velocity:
$\ell > \ell _\chi$ obeys the same scaling as the bulk velocity:
 \begin{equation} \frac{T\!\left(\ell\right)}{T(L_0)} \sim \frac{V\!\left(\ell\right)}{V_0} \sim \left(\frac{{Pe}_\ell}{Pe} \right)^{1/4} . \end{equation}
\begin{equation} \frac{T\!\left(\ell\right)}{T(L_0)} \sim \frac{V\!\left(\ell\right)}{V_0} \sim \left(\frac{{Pe}_\ell}{Pe} \right)^{1/4} . \end{equation}
In addition, the magnitude of temperature fluctuations at the driving scale is related to the mean temperature by the Mach number of the driving-scale motions, ![]() $T(L_0) \sim T_0 {Ma}_0$, which then gives
$T(L_0) \sim T_0 {Ma}_0$, which then gives
 \begin{equation} \frac{T\!\left(\ell\right)}{T_0} \sim {Ma}_0 \left(\frac{{Pe}_\ell}{Pe} \right)^{1/4} , \end{equation}
\begin{equation} \frac{T\!\left(\ell\right)}{T_0} \sim {Ma}_0 \left(\frac{{Pe}_\ell}{Pe} \right)^{1/4} , \end{equation}
where ![]() ${Pe} \equiv {Pe}_{L_0}$. It follows from an analogous argument to that just given for the velocity fluctuations that
${Pe} \equiv {Pe}_{L_0}$. It follows from an analogous argument to that just given for the velocity fluctuations that
Under Braginskii's ordering, the Prandtl number of CE plasma is
and, therefore,
 \begin{equation} L_T \sim \ell_{\chi} \frac{T_0}{T\!\left(\ell_\chi\right)} \sim L_0 \mu_e^{{-}1/4} {Ma}_0^{{-}3/2} \left(\frac{\lambda_{i}}{L_0}\right)^{1/2} . \end{equation}
\begin{equation} L_T \sim \ell_{\chi} \frac{T_0}{T\!\left(\ell_\chi\right)} \sim L_0 \mu_e^{{-}1/4} {Ma}_0^{{-}3/2} \left(\frac{\lambda_{i}}{L_0}\right)^{1/2} . \end{equation}
Thus, ![]() $L_V \sim {Ma}_0 \mu _e^{1/4} L_T \ll L_T$ under the assumed ordering.
$L_V \sim {Ma}_0 \mu _e^{1/4} L_T \ll L_T$ under the assumed ordering.
Finally, we consider whether our a priori assumption that ![]() $L_{T_i} \sim L_T$ is, in fact, justified. A sufficient condition for ion-temperature gradients to be the same as electron-temperature gradients is for the evolution time
$L_{T_i} \sim L_T$ is, in fact, justified. A sufficient condition for ion-temperature gradients to be the same as electron-temperature gradients is for the evolution time ![]() $\tau _{L}$ of all macroscopic motions to be much longer than the ion–electron equilibration-time
$\tau _{L}$ of all macroscopic motions to be much longer than the ion–electron equilibration-time ![]() $\tau _{ie}^{\rm eq}$ defined by (2.40). Since
$\tau _{ie}^{\rm eq}$ defined by (2.40). Since ![]() $\tau _{L} \gtrsim {\ell _\nu }/{V(\ell _\nu )}$, it follows that
$\tau _{L} \gtrsim {\ell _\nu }/{V(\ell _\nu )}$, it follows that
 \begin{equation} \frac{\tau_{L}}{\tau_{ie}^{\rm eq}} \sim \left(\frac{m_i}{m_e}\right)^{1/2}{Ma}_0^{3/2} \left(\frac{\lambda_i}{L_0}\right)^{1/2} \sim \epsilon_i \left(\frac{m_i}{m_e}\right)^{1/2} . \end{equation}
\begin{equation} \frac{\tau_{L}}{\tau_{ie}^{\rm eq}} \sim \left(\frac{m_i}{m_e}\right)^{1/2}{Ma}_0^{3/2} \left(\frac{\lambda_i}{L_0}\right)^{1/2} \sim \epsilon_i \left(\frac{m_i}{m_e}\right)^{1/2} . \end{equation}
Thus, if ![]() $\epsilon _i \gg \mu _e^{1/2}$, we conclude that collisional equilibration of ion and electron temperatures might be too inefficient to regulate small-scale ion-temperature fluctuations, in which case it would follow that
$\epsilon _i \gg \mu _e^{1/2}$, we conclude that collisional equilibration of ion and electron temperatures might be too inefficient to regulate small-scale ion-temperature fluctuations, in which case it would follow that ![]() $L_{T_i} < L_{T}$. However, it has been previously demonstrated via numerical solution of the Vlasov–Fokker–Planck equation that the CE expansion procedure breaks down due to non-local transport effects if
$L_{T_i} < L_{T}$. However, it has been previously demonstrated via numerical solution of the Vlasov–Fokker–Planck equation that the CE expansion procedure breaks down due to non-local transport effects if ![]() $\lambda _e/L$ is only moderately small (Bell, Evans & Nicholas Reference Bell, Evans and Nicholas1981); thus, the only regime in which there is not ion–electron equilibration over all scales is one where the CE expansion is not valid anyway. In short, we conclude that assuming
$\lambda _e/L$ is only moderately small (Bell, Evans & Nicholas Reference Bell, Evans and Nicholas1981); thus, the only regime in which there is not ion–electron equilibration over all scales is one where the CE expansion is not valid anyway. In short, we conclude that assuming ![]() $L_{T_i} \sim L_T$ is reasonable.
$L_{T_i} \sim L_T$ is reasonable.
Bringing these considerations together with (2.42), we find that
 $$\begin{align} &\eta_e^T \sim \mu_e^{1/4} {Ma}_0 \frac{\lambda_i}{L_V} \sim {Ma}_0^{3/2} \mu_e^{1/4} \left(\frac{\lambda_i}{L_0}\right)^{1/2} \sim \eta_e^{R} \sim \eta_e^{u} \sim \eta_i , \end{align}$$
$$\begin{align} &\eta_e^T \sim \mu_e^{1/4} {Ma}_0 \frac{\lambda_i}{L_V} \sim {Ma}_0^{3/2} \mu_e^{1/4} \left(\frac{\lambda_i}{L_0}\right)^{1/2} \sim \eta_e^{R} \sim \eta_e^{u} \sim \eta_i , \end{align}$$ $$\begin{align} &\epsilon_e \sim \mu_e^{1/2} {Ma}_0 \frac{\lambda_i}{L_V}\sim \mu_e^{1/2} {Ma}_0^{3/2} \left(\frac{\lambda_i}{L_0}\right)^{1/2} , \end{align}$$
$$\begin{align} &\epsilon_e \sim \mu_e^{1/2} {Ma}_0 \frac{\lambda_i}{L_V}\sim \mu_e^{1/2} {Ma}_0^{3/2} \left(\frac{\lambda_i}{L_0}\right)^{1/2} , \end{align}$$ $$\begin{align} &\epsilon_i \sim {Ma}_0 \frac{\lambda_i}{L_V} \sim {Ma}_0^{3/2} \left(\frac{\lambda_i}{L_0}\right)^{1/2} . \end{align}$$
$$\begin{align} &\epsilon_i \sim {Ma}_0 \frac{\lambda_i}{L_V} \sim {Ma}_0^{3/2} \left(\frac{\lambda_i}{L_0}\right)^{1/2} . \end{align}$$Thus, we conclude that the largest distortions of the ion CE distribution are due to flow gradients, while temperature gradients cause the greatest distortions of the electron CE distribution function.
In deriving the estimates (2.55) of the small parameters ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$,
$\eta _e^u$, ![]() $\eta _i$,
$\eta _i$, ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$, we assumed that the motions of the plasma (including those at the Kolmogorov scale) satisfied Kolmogorov's statistical theory of turbulence. There are several reasonable grounds on which this assumption could be questioned. First of these is intermittency: it is a long-standing result that the distribution of turbulent velocities at a given scale in hydrodynamic turbulence becomes increasingly non-Gaussian as that scale decreases (see, e.g. Davidson Reference Davidson2015). This has the consequence that (2.55) may overestimate the size of the non-Maxwellian terms in the CE distribution function for the majority of the plasma's volume, but underestimate it significantly in localised regions. Another objection is the now generally accepted finding that turbulent fluids with sufficiently strong magnetic fields do not behave like hydrodynamic fluids: instead, turbulent motions tend to become anisotropic with respect to the background magnetic field if the latter's energy becomes greater than the former (Goldreich & Sridhar Reference Goldreich and Sridhar1995; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). When applied to turbulent motions at the Kolmogorov scale where motions are assumed to behave as we have proposed, this condition becomes
$\epsilon _i$, we assumed that the motions of the plasma (including those at the Kolmogorov scale) satisfied Kolmogorov's statistical theory of turbulence. There are several reasonable grounds on which this assumption could be questioned. First of these is intermittency: it is a long-standing result that the distribution of turbulent velocities at a given scale in hydrodynamic turbulence becomes increasingly non-Gaussian as that scale decreases (see, e.g. Davidson Reference Davidson2015). This has the consequence that (2.55) may overestimate the size of the non-Maxwellian terms in the CE distribution function for the majority of the plasma's volume, but underestimate it significantly in localised regions. Another objection is the now generally accepted finding that turbulent fluids with sufficiently strong magnetic fields do not behave like hydrodynamic fluids: instead, turbulent motions tend to become anisotropic with respect to the background magnetic field if the latter's energy becomes greater than the former (Goldreich & Sridhar Reference Goldreich and Sridhar1995; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). When applied to turbulent motions at the Kolmogorov scale where motions are assumed to behave as we have proposed, this condition becomes
 \begin{equation} \frac{m_i n_i V(\ell_{\nu})^2/2}{B^2/8{\rm \pi}} \sim \frac{m_i n_i V_0^2/2}{B^2/8{\rm \pi}} \frac{V(\ell_{\nu})^2}{V_0^2} \sim {Ma}_0^{3/2} \left(\frac{\lambda_i}{L_0}\right)^{1/2} \beta_i \sim \epsilon_i \beta_i , \end{equation}
\begin{equation} \frac{m_i n_i V(\ell_{\nu})^2/2}{B^2/8{\rm \pi}} \sim \frac{m_i n_i V_0^2/2}{B^2/8{\rm \pi}} \frac{V(\ell_{\nu})^2}{V_0^2} \sim {Ma}_0^{3/2} \left(\frac{\lambda_i}{L_0}\right)^{1/2} \beta_i \sim \epsilon_i \beta_i , \end{equation}where
is the plasma beta of species ![]() $s$. So, whenever
$s$. So, whenever ![]() $\beta _i \ll \epsilon _i^{-1}$, the assumption that the turbulence is unmagnetised is unlikely to be a good one, whereas if
$\beta _i \ll \epsilon _i^{-1}$, the assumption that the turbulence is unmagnetised is unlikely to be a good one, whereas if ![]() $\beta _i$ is sufficiently large (
$\beta _i$ is sufficiently large (![]() $\beta _i \gtrsim \epsilon _i^{-1}$), it is more reasonable. As we have already outlined in the introduction (cf. figure 1), the case in which
$\beta _i \gtrsim \epsilon _i^{-1}$), it is more reasonable. As we have already outlined in the introduction (cf. figure 1), the case in which ![]() $\beta _i$ is large will tend to be our focus in this paper; so we conclude that the scalings (2.55) will generally be the pertinent ones.
$\beta _i$ is large will tend to be our focus in this paper; so we conclude that the scalings (2.55) will generally be the pertinent ones.
2.3. Kinetic stability of classical, collisional plasma
2.3.1. Overview
We have seen that the CE expansion provides a procedure for the calculation of the distribution functions arising in a classical, collisional plasma in terms of gradients of temperature, electron–ion drifts and bulk fluid velocities; these calculations in turn allow for the closure of the system (2.4) of fluid equations. However, these same gradients are sources of free energy in the plasma, so they can lead to instabilities. Some of these instabilities will be ‘fluid’, i.e. they are captured within the CE description and are features of the fluid dynamics of plasmas; others are kinetic (‘microinstabilities’), and their existence implies that the CE expansion is, in fact, illegitimate. Our primary purpose in this paper is to determine when such microinstabilities do not occur in a strongly magnetised two-species plasma. If, however, they do occur, we wish to determine their growth rates. We begin by making a few general qualitative comments concerning the existence and nature of these microinstabilities, before presenting the technical details of their derivation.
2.3.2. Existence of microinstabilities in classical, collisional plasma
It might naively be assumed that a classical, collisional plasma is kinetically stable, on two grounds. The first of these is that the distribution function of such a plasma is ‘almost’ Maxwellian, and thus stable. While it is certainly the case that a plasma whose constituent particles have Maxwellian distribution functions is kinetically stable (Bernstein Reference Bernstein1958; Krall & Trivelpiece Reference Krall and Trivelpiece1973), it is also known that a plasma with anisotropic particle distribution functions is typically not (Furth Reference Furth1963; Kalman et al. Reference Kalman, Montes and Quemada1968; Davidson Reference Davidson1983; Gary Reference Gary1993). The (small) non-Maxwellian component of the CE distribution function is anisotropic (as, e.g. was explicitly demonstrated by the calculation of pressure anisotropy in § 2.2.2), and thus we cannot a priori rule out microinstabilities associated with this anisotropy.
The second naive reason for dismissing the possibility of microinstabilities in classical, collisional plasma is the potentially stabilising effect of collisional damping on microinstability growth rates. If collisional processes are sufficiently dominant to be responsible for the mediation of macroscopic momentum and heat fluxes in the plasma, it might be naively inferred that they would also suppress microinstabilities. This is, in fact, far from guaranteed, for the following reason. The characteristic scales of the microinstabilities are not fluid scales, but are rather intrinsic plasma length scales related to quantities such as the Larmor radius ![]() $\rho _s$ or the inertial scale
$\rho _s$ or the inertial scale ![]() $d_s$ of species
$d_s$ of species ![]() $s$, or the Debye length
$s$, or the Debye length ![]() $\lambda _{{\rm D}}$ – quantities given in terms of macroscopic physical properties of plasma by
$\lambda _{{\rm D}}$ – quantities given in terms of macroscopic physical properties of plasma by
 $$\begin{align} &d_s \equiv \left(\frac{4 {\rm \pi}Z_s^2 e^2 n_s}{m_s c^2}\right)^{{-}1/2} = \rho_s \beta_s^{{-}1/2}, \end{align}$$
$$\begin{align} &d_s \equiv \left(\frac{4 {\rm \pi}Z_s^2 e^2 n_s}{m_s c^2}\right)^{{-}1/2} = \rho_s \beta_s^{{-}1/2}, \end{align}$$ $$\begin{align} &\lambda_{{\rm D}} \equiv \left(\sum_s \frac{4 {\rm \pi}Z_s^2 e^2 n_s}{T_s}\right)^{{-}1/2} = \left(\sum_s \frac{2 c}{d_s^2 v_{\mathrm{th}s}} \right)^{{-}1/2} . \end{align}$$
$$\begin{align} &\lambda_{{\rm D}} \equiv \left(\sum_s \frac{4 {\rm \pi}Z_s^2 e^2 n_s}{T_s}\right)^{{-}1/2} = \left(\sum_s \frac{2 c}{d_s^2 v_{\mathrm{th}s}} \right)^{{-}1/2} . \end{align}$$
The crucial observation is then that the dynamics on characteristic microinstability scales may be collisionless. For a classical, collisional hydrogen plasma (where ![]() $\lambda \equiv \lambda _e \sim \lambda _i$ for
$\lambda \equiv \lambda _e \sim \lambda _i$ for ![]() $T_e \sim T_i$), the mean free path is much larger than the Debye length:
$T_e \sim T_i$), the mean free path is much larger than the Debye length: ![]() $\lambda /\lambda _{{\rm D}} \sim n_e \lambda _{{\rm D}}^3 \gg 1$; so there exists a range of wavenumbers
$\lambda /\lambda _{{\rm D}} \sim n_e \lambda _{{\rm D}}^3 \gg 1$; so there exists a range of wavenumbers ![]() $k$ on which microinstabilities are both possible (
$k$ on which microinstabilities are both possible (![]() $k \lambda _{{\rm D}} \lesssim 1$) and collisionless (
$k \lambda _{{\rm D}} \lesssim 1$) and collisionless (![]() $k \lambda \gg 1$). For a strongly magnetised collisional plasma,
$k \lambda \gg 1$). For a strongly magnetised collisional plasma, ![]() $\lambda _s \gg \rho _s$ for all species by definition; thus, any microinstability with a characteristic scale comparable to the Larmor radius of any constituent particle will be effectively collisionless. We note that such a range of collisionless wavenumbers only exists in classical (viz. weakly coupled) plasmas; in strongly coupled plasmas, for which
$\lambda _s \gg \rho _s$ for all species by definition; thus, any microinstability with a characteristic scale comparable to the Larmor radius of any constituent particle will be effectively collisionless. We note that such a range of collisionless wavenumbers only exists in classical (viz. weakly coupled) plasmas; in strongly coupled plasmas, for which ![]() $\lambda \lesssim \lambda _{{\rm D}}$, all hypothetically possible microinstability wavenumber scales are collisional. Thus the phenomenon of microinstabilities in collisional plasmas is solely a concern for the classical regime.
$\lambda \lesssim \lambda _{{\rm D}}$, all hypothetically possible microinstability wavenumber scales are collisional. Thus the phenomenon of microinstabilities in collisional plasmas is solely a concern for the classical regime.
2.3.3. A simple example: the firehose instability in CE plasmas
Perhaps the simplest example of a microinstability that can occur in CE plasma is the firehose instability. This example was previously discussed by Schekochihin et al. (Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005), but we nonetheless outline it here to illustrate the central concept of our paper.
Consider bulk fluid motions of the plasma on length scales ![]() $L_V$ that are much smaller than the mean free path
$L_V$ that are much smaller than the mean free path ![]() $\lambda _i$, but much larger than the ion-Larmor radius
$\lambda _i$, but much larger than the ion-Larmor radius ![]() $\rho _i$; the characteristic frequencies associated with these motions are assumed to be much smaller that the ion Larmor frequency
$\rho _i$; the characteristic frequencies associated with these motions are assumed to be much smaller that the ion Larmor frequency ![]() $\varOmega _i$, but much larger than the inverse of the ion collision time
$\varOmega _i$, but much larger than the inverse of the ion collision time ![]() $\tau _{i}^{-1}$. Under these assumptions, the following four statements can be shown to be true (Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005):
$\tau _{i}^{-1}$. Under these assumptions, the following four statements can be shown to be true (Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005):
(i) The bulk velocities of the electron and ion species are approximately equal:
 $\boldsymbol {V}_e \approx \boldsymbol {V}_i$.
$\boldsymbol {V}_e \approx \boldsymbol {V}_i$.(ii) The electric field in a frame co-moving with the ion fluid vanishes; transforming to the stationary frame of the system, this gives
(2.59) \begin{equation} \boldsymbol{E} ={-}\frac{\boldsymbol{V}_i \times \boldsymbol{B}}{c} . \end{equation}
\begin{equation} \boldsymbol{E} ={-}\frac{\boldsymbol{V}_i \times \boldsymbol{B}}{c} . \end{equation}(iii) The contribution of the displacement current to the Maxwell–Ampère law (2.2d) is negligible, and so
(2.60) \begin{equation} e n_e \left(\boldsymbol{V}_i - \boldsymbol{V}_e \right) \approx \frac{c}{4 {\rm \pi}} \boldsymbol{\nabla} \times \boldsymbol{B} . \end{equation}
\begin{equation} e n_e \left(\boldsymbol{V}_i - \boldsymbol{V}_e \right) \approx \frac{c}{4 {\rm \pi}} \boldsymbol{\nabla} \times \boldsymbol{B} . \end{equation}(iv) The electron and ion viscosity tensors both take the form (2.32), and the electron-pressure anisotropy, defined by (2.35), is small compared with the ion pressure anisotropy:
 $\varDelta _e \ll \varDelta _i$.
$\varDelta _e \ll \varDelta _i$.
It then follows directly from (2.4b), summed over both ion and electron species, that
We remind the reader that ![]() $\hat {\boldsymbol {z}} = \boldsymbol {B}/B$, and emphasise that we have neglected the electron inertial term on the grounds that it is small compared with the ion inertial term:
$\hat {\boldsymbol {z}} = \boldsymbol {B}/B$, and emphasise that we have neglected the electron inertial term on the grounds that it is small compared with the ion inertial term:
The evolution of the magnetic field is described by the induction equation
which is derived by substituting (2.59) into Faraday's law (2.2c).
Now consider small-amplitude perturbations with respect to a particular macroscale state of the plasma
whose characteristic frequency ![]() $\omega$ is much greater than that of the plasma's bulk fluid motions (but is still much smaller than
$\omega$ is much greater than that of the plasma's bulk fluid motions (but is still much smaller than ![]() $\varOmega _i$), whose wavevector
$\varOmega _i$), whose wavevector ![]() $\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$ is parallel to
$\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$ is parallel to ![]() $\boldsymbol {B}$, and assume also that the velocity and magnetic-field perturbations are perpendicular to
$\boldsymbol {B}$, and assume also that the velocity and magnetic-field perturbations are perpendicular to ![]() $\boldsymbol {B}$. It is then easy to show that (2.61) and (2.63) become
$\boldsymbol {B}$. It is then easy to show that (2.61) and (2.63) become
 $$\begin{align} - \mathrm{i} m_i n_i \omega \widehat{\delta \boldsymbol{V}}_{i\perp} &= \mathrm{i} \left(\frac{B^2}{4 {\rm \pi}} + p_{i\perp} - p_{i\|}\right) k_{\|} \frac{ \widehat{\delta \boldsymbol{B}}_{{\perp}} }{B} , \end{align}$$
$$\begin{align} - \mathrm{i} m_i n_i \omega \widehat{\delta \boldsymbol{V}}_{i\perp} &= \mathrm{i} \left(\frac{B^2}{4 {\rm \pi}} + p_{i\perp} - p_{i\|}\right) k_{\|} \frac{ \widehat{\delta \boldsymbol{B}}_{{\perp}} }{B} , \end{align}$$
where ![]() $p_{i\perp }$ and
$p_{i\perp }$ and ![]() $p_{i\|}$ are the perpendicular and parallel ion pressures associated with the macroscale state (which, on account of its comparatively slow evolution compared with the perturbation, can be regarded a quasi-equilibrium). Physically, the macroscale flow gives rise to different values of
$p_{i\|}$ are the perpendicular and parallel ion pressures associated with the macroscale state (which, on account of its comparatively slow evolution compared with the perturbation, can be regarded a quasi-equilibrium). Physically, the macroscale flow gives rise to different values of ![]() $p_{i\perp }$ and
$p_{i\perp }$ and ![]() $p_{i\|}$, and thereby an ion-pressure anisotropy
$p_{i\|}$, and thereby an ion-pressure anisotropy ![]() $\varDelta _i$, because it changes the strength
$\varDelta _i$, because it changes the strength ![]() $B$ of the macroscale magnetic field; thanks to the effective conservation of the first and second adiabatic moments of the ions on the evolution time scale of the macroscale flow (Chew et al. Reference Chew, Goldberger, Low and Chandrasekhar1956), an increase (decrease) in
$B$ of the macroscale magnetic field; thanks to the effective conservation of the first and second adiabatic moments of the ions on the evolution time scale of the macroscale flow (Chew et al. Reference Chew, Goldberger, Low and Chandrasekhar1956), an increase (decrease) in ![]() $B$ results in an increase (decrease) in
$B$ results in an increase (decrease) in ![]() $p_{i\perp }$, and a decrease (increase) in
$p_{i\perp }$, and a decrease (increase) in ![]() $p_{i\|}$. The dispersion relation for the perturbation is then
$p_{i\|}$. The dispersion relation for the perturbation is then
where ![]() $\beta _i$, defined by (2.57), is the ion plasma beta. For a sufficiently negative ion-pressure anisotropy, viz.
$\beta _i$, defined by (2.57), is the ion plasma beta. For a sufficiently negative ion-pressure anisotropy, viz. ![]() $\varDelta _i < -2/\beta _i$, the perturbation is unstable. This instability is known as the (parallel) firehose instability.
$\varDelta _i < -2/\beta _i$, the perturbation is unstable. This instability is known as the (parallel) firehose instability.
The underlying physics of the parallel firehose instability has been discussed extensively elsewhere (see Rosin et al. (Reference Rosin, Schekochihin, Rincon and Cowley2011), and references therein; also see § 4.4.1). Here, we simply note that the firehose instability arises in a magnetised plasma with sufficiently negative pressure anisotropy as compared with the inverse of the ion plasma beta; because the ion CE distribution function has a small, non-zero pressure anisotropy, this statement applies to CE plasma at large ![]() $\beta _i$. We also observe that the product of the growth rate (2.66) of the firehose instability with the ion–ion collision time satisfies
$\beta _i$. We also observe that the product of the growth rate (2.66) of the firehose instability with the ion–ion collision time satisfies
 \begin{equation} \omega \tau_i \sim k_{\|} \lambda_i \left|\frac{1}{\beta_i} + \varDelta_i \right|^{1/2} \sim \frac{1}{\beta_i} \frac{\lambda_i}{\rho_i} , \end{equation}
\begin{equation} \omega \tau_i \sim k_{\|} \lambda_i \left|\frac{1}{\beta_i} + \varDelta_i \right|^{1/2} \sim \frac{1}{\beta_i} \frac{\lambda_i}{\rho_i} , \end{equation}
where we have assumed that ![]() $\varDelta _i \lesssim -2 \beta _i^{-1}$, and employed the (non-trivial) result that the peak growth of the parallel firehose instability occurs at wavenumbers satisfying
$\varDelta _i \lesssim -2 \beta _i^{-1}$, and employed the (non-trivial) result that the peak growth of the parallel firehose instability occurs at wavenumbers satisfying ![]() $k_{\|} \rho _i \sim \beta _i^{-1/2}$ (see §§ 4.4.1 and 4.4.2). Thus, if
$k_{\|} \rho _i \sim \beta _i^{-1/2}$ (see §§ 4.4.1 and 4.4.2). Thus, if ![]() $\beta _i \ll \lambda _i/\rho _i$ – a condition easily satisfied in weakly collisional astrophysical environments such as the ICM (see table 4) – it follows that
$\beta _i \ll \lambda _i/\rho _i$ – a condition easily satisfied in weakly collisional astrophysical environments such as the ICM (see table 4) – it follows that ![]() $\omega \tau _i \gg 1$, and so collisional damping is unable to inhibit the parallel firehose in a CE plasma.Footnote 2 This failure is directly attributable to its characteristic wavelength being at collisionless scales: the parallel wavenumber satisfies
$\omega \tau _i \gg 1$, and so collisional damping is unable to inhibit the parallel firehose in a CE plasma.Footnote 2 This failure is directly attributable to its characteristic wavelength being at collisionless scales: the parallel wavenumber satisfies ![]() $k_{\|} \lambda _i \sim \beta _i^{-1/2} \lambda _i/\rho _i \gg 1$.
$k_{\|} \lambda _i \sim \beta _i^{-1/2} \lambda _i/\rho _i \gg 1$.
This simple example clearly illustrates that microinstabilities are indeed possible in a classical, collisional plasma, for precisely the reasons given in § 2.3.2.
2.3.4. Which microinstabilities are relevant
Although the naive arguments described in § 2.3.2 do not imply kinetic stability of CE plasma, these same arguments do lead to significant restrictions on the type of microinstabilities that can arise. Namely, for some plasma modes, the small anisotropy of CE distribution functions is an insufficient free-energy source for overcoming the competing collisionless damping mechanisms that ensure stability for pure Maxwellian distribution functions – e.g. Landau damping or cyclotron damping. For other plasma modes, the characteristic length scales are so large that collisional damping does suppress growth. In magnetised plasmas, there also exist cyclotron harmonic oscillations that, despite minimal damping, can only become unstable for sufficiently large anisotropy of the particle distribution function: e.g. the electrostatic Harris instability (Harris Reference Harris1959; Hall, Heckrotte & Kammash Reference Hall, Heckrotte and Kammash1964). Since the anisotropy threshold for such microinstabilities is typically ![]() $\varDelta _s \gtrsim 1$ (Shima & Hall Reference Shima and Hall1965), they cannot operate in a CE plasma.
$\varDelta _s \gtrsim 1$ (Shima & Hall Reference Shima and Hall1965), they cannot operate in a CE plasma.
We claim that there are only two classes of microinstabilities that can be triggered in a CE plasma. The first are quasi-cold-plasma modes: these are modes whose frequency is so large that resonant wave–particle interactions (Landau or cyclotron resonances) only occur with electrons whose speed greatly exceeds the electron thermal speed ![]() $v_{\mathrm {th}e}$. Collisionless damping of such modes is typically very weak, and thus small anisotropies of particle distribution functions can be sufficient to drive an instability. Well-known examples of a small non-Maxwellian part of the distribution function giving rise to microinstabilities include the bump-on-tail instability associated with a fast beam of electrons (see § 3.3.3 of Davidson Reference Davidson1983), or the whistler instability for small temperature anisotropies (see § 3.3.5 of Davidson Reference Davidson1983). The existence of such instabilities for the CE distribution can be demonstrated explicitly: e.g. the peak growth rate of the bump-on-tail instability associated with the CE distribution function (‘the CE bump-on-tail instability’) is calculated in Appendix D.3. However, the growth rates
$v_{\mathrm {th}e}$. Collisionless damping of such modes is typically very weak, and thus small anisotropies of particle distribution functions can be sufficient to drive an instability. Well-known examples of a small non-Maxwellian part of the distribution function giving rise to microinstabilities include the bump-on-tail instability associated with a fast beam of electrons (see § 3.3.3 of Davidson Reference Davidson1983), or the whistler instability for small temperature anisotropies (see § 3.3.5 of Davidson Reference Davidson1983). The existence of such instabilities for the CE distribution can be demonstrated explicitly: e.g. the peak growth rate of the bump-on-tail instability associated with the CE distribution function (‘the CE bump-on-tail instability’) is calculated in Appendix D.3. However, the growth rates ![]() $\gamma$ of such instabilities are exponentially small in
$\gamma$ of such instabilities are exponentially small in ![]() $\lambda _e/L \ll 1$. This claim, which is explicitly proven for the CE bump-on-tail instability in Appendix D.3, applies to all electrostatic instabilities (see Appendix D.4), and it can be argued that it also applies to all quasi-cold-plasma modes (see Appendix E). When combined with the constraint that the resonant wave–particle interactions required for such instabilities cannot occur if
$\lambda _e/L \ll 1$. This claim, which is explicitly proven for the CE bump-on-tail instability in Appendix D.3, applies to all electrostatic instabilities (see Appendix D.4), and it can be argued that it also applies to all quasi-cold-plasma modes (see Appendix E). When combined with the constraint that the resonant wave–particle interactions required for such instabilities cannot occur if ![]() $\gamma \tau _{r} \lesssim 1$, where
$\gamma \tau _{r} \lesssim 1$, where ![]() $\tau _{r}$ is the collision time of the resonant particles, the exponential smallness of the growth rate suggests that such microinstabilities will not be significant provided
$\tau _{r}$ is the collision time of the resonant particles, the exponential smallness of the growth rate suggests that such microinstabilities will not be significant provided ![]() $\lambda _e/L$ really is small. As discussed in § 2.2.3, plasmas in which
$\lambda _e/L$ really is small. As discussed in § 2.2.3, plasmas in which ![]() $\lambda _e/L$ is only moderately small are not well modelled as CE plasmas anyway, and thus, for the rest of this paper, we will not study quasi-cold-plasma-mode instabilities.
$\lambda _e/L$ is only moderately small are not well modelled as CE plasmas anyway, and thus, for the rest of this paper, we will not study quasi-cold-plasma-mode instabilities.
The second class of allowed microinstabilities comprises modes that are electromagnetic and low frequency in the sense that the complex frequency ![]() $\omega$ of the microinstability satisfies, for at least one particle species
$\omega$ of the microinstability satisfies, for at least one particle species ![]() $s$,
$s$,
where ![]() $\iota$ is some order-unity number. Low-frequency electromagnetic modes are in general only subject to weak Landau and cyclotron damping (of order
$\iota$ is some order-unity number. Low-frequency electromagnetic modes are in general only subject to weak Landau and cyclotron damping (of order ![]() $\omega /k v_{\mathrm {th}s} \ll 1$ or less), and thus can become unstable for small distribution-function anisotropies. By contrast, electromagnetic modes satisfying
$\omega /k v_{\mathrm {th}s} \ll 1$ or less), and thus can become unstable for small distribution-function anisotropies. By contrast, electromagnetic modes satisfying ![]() $\omega \sim k v_{\mathrm {th}s}$ would typically generate strong inductive electric fields, which would in turn be subject to significant Landau or cyclotron damping, overwhelming any unstable tendency. The firehose instability introduced in § 2.3.3 is one example of this type of microinstability: it satisfies (2.68) with
$\omega \sim k v_{\mathrm {th}s}$ would typically generate strong inductive electric fields, which would in turn be subject to significant Landau or cyclotron damping, overwhelming any unstable tendency. The firehose instability introduced in § 2.3.3 is one example of this type of microinstability: it satisfies (2.68) with ![]() $\iota = 1/2$, provided its
$\iota = 1/2$, provided its ![]() $\beta$-stabilisation threshold is surpassed.
$\beta$-stabilisation threshold is surpassed.
In this paper, we will focus on microinstabilities in this second class. Whilst small compared with the streaming rate ![]() $k v_{\mathrm {th}s}$ of species
$k v_{\mathrm {th}s}$ of species ![]() $s$, the growth rates satisfying (2.68) can still be significantly larger than the rate at which the plasma evolves on macroscopic scales, and thus invalidate the CE expansion. We do not in this paper present a rigorous proof that there are no microinstabilities of the CE distribution function which do not fall into either of the two classes considered above. However, there do exist more precise arguments supporting the latter claim than those based on physical intuition just presented; these are discussed further in §§ 2.4.2 and 2.5.8.
$s$, the growth rates satisfying (2.68) can still be significantly larger than the rate at which the plasma evolves on macroscopic scales, and thus invalidate the CE expansion. We do not in this paper present a rigorous proof that there are no microinstabilities of the CE distribution function which do not fall into either of the two classes considered above. However, there do exist more precise arguments supporting the latter claim than those based on physical intuition just presented; these are discussed further in §§ 2.4.2 and 2.5.8.
The microinstabilities satisfying (2.68) fall into two sub-classes. The first sub-class consists of microinstabilities driven by the CE temperature-gradient, CE electron-friction and CE electron–ion-drift terms in the CE distribution functions (2.8); we refer to these collectively as CE temperature-gradient-driven microinstabilities, or CET microinstabilities, on account of the parameters ![]() $\eta _e^R$ and
$\eta _e^R$ and ![]() $\eta _e^u$ scaling with temperature gradients (see § 2.2.2). The second sub-class is microinstabilities driven by the CE shear terms, or CE shear-driven microinstabilities (CES microinstabilities). This sub-classification is necessary for two reasons. First, the velocity-space anisotropy associated with the CE shear terms is different from other non-Maxwellian terms, and thus different types of microinstabilities can emerge for the two sub-classes. Secondly, as was discussed in § 2.2.3 for the case of CE plasma, the typical size of small parameters
$\eta _e^u$ scaling with temperature gradients (see § 2.2.2). The second sub-class is microinstabilities driven by the CE shear terms, or CE shear-driven microinstabilities (CES microinstabilities). This sub-classification is necessary for two reasons. First, the velocity-space anisotropy associated with the CE shear terms is different from other non-Maxwellian terms, and thus different types of microinstabilities can emerge for the two sub-classes. Secondly, as was discussed in § 2.2.3 for the case of CE plasma, the typical size of small parameters ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _e^u$ and
$\eta _e^u$ and ![]() $\eta _i$ is different from that of
$\eta _i$ is different from that of ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$. In our initial overview of our calculations (§ 2.4) and in the more detailed discussion of our method (§ 2.5), we will consider all microinstabilities driven by the non-Maxwellian terms of the CE distribution together; however, when it comes to presenting detailed results, we will consider CET and CES microinstabilities separately (§§ 3 and 4, respectively).
$\epsilon _i$. In our initial overview of our calculations (§ 2.4) and in the more detailed discussion of our method (§ 2.5), we will consider all microinstabilities driven by the non-Maxwellian terms of the CE distribution together; however, when it comes to presenting detailed results, we will consider CET and CES microinstabilities separately (§§ 3 and 4, respectively).
2.4. Linear stability calculation: overview
2.4.1. General dispersion relation
Our linear kinetic stability calculation proceeds as follows: we consider an electromagnetic perturbation with wavevector ![]() $\boldsymbol {k}$ and (complex) frequency
$\boldsymbol {k}$ and (complex) frequency ![]() $\omega$ of the form
$\omega$ of the form
in a plasma with the equilibrium electron and ion distribution functions given by (2.8a) and (2.8b), respectively. We assume that all macroscopic parameters in the CE distribution function are effectively constant on the time scales and length scales associated with microinstabilities: this is equivalent to assuming that ![]() $k \lambda _e, k \lambda _i \gg 1$ (where
$k \lambda _e, k \lambda _i \gg 1$ (where ![]() $k \equiv |\boldsymbol {k}|$ is the wavenumber of the perturbation), and
$k \equiv |\boldsymbol {k}|$ is the wavenumber of the perturbation), and ![]() $|\omega | \tau _L \gg 1$. To minimise confusion between quantities evolving on short, collisionless time scales, and those on long, fluid time scales, we relabel the equilibrium number density of species
$|\omega | \tau _L \gg 1$. To minimise confusion between quantities evolving on short, collisionless time scales, and those on long, fluid time scales, we relabel the equilibrium number density of species ![]() $s$ as
$s$ as ![]() $n_{s0}$, and the macroscopic magnetic field as
$n_{s0}$, and the macroscopic magnetic field as ![]() $\boldsymbol {B}_0$ in subsequent calculations. For notational convenience, we define
$\boldsymbol {B}_0$ in subsequent calculations. For notational convenience, we define
and
which in turn allows for the equilibrium distribution function of species ![]() $s$ to be written as
$s$ to be written as
Finally, without loss of generality, we can set ![]() $\boldsymbol {V}_{i} = 0$ by choosing to perform the kinetic calculation in the frame of the ions; thus,
$\boldsymbol {V}_{i} = 0$ by choosing to perform the kinetic calculation in the frame of the ions; thus, ![]() $\tilde {\boldsymbol {v}}_s = \boldsymbol {v}/v_{\mathrm {th}s}$.
$\tilde {\boldsymbol {v}}_s = \boldsymbol {v}/v_{\mathrm {th}s}$.
It is well known (Stix Reference Stix1962; Parra Reference Parra2017) that the electric field of all linear electromagnetic perturbations in a collisionless, magnetised plasma with equilibrium distribution function ![]() $f_{s0}$ must satisfy
$f_{s0}$ must satisfy
where ![]() $\hat {\boldsymbol {k}} \equiv \boldsymbol {k}/k$ is the direction of the perturbation,
$\hat {\boldsymbol {k}} \equiv \boldsymbol {k}/k$ is the direction of the perturbation,
the plasma dielectric tensor and ![]() $\boldsymbol {\sigma }$ the plasma conductivity tensor. The hot-plasma dispersion relation is then given by
$\boldsymbol {\sigma }$ the plasma conductivity tensor. The hot-plasma dispersion relation is then given by
The conductivity tensor in a hot, magnetised plasma is best displayed in an orthogonal coordinate system with basis vectors ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ defined in terms of
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ defined in terms of ![]() $\boldsymbol {B}_0$ and
$\boldsymbol {B}_0$ and ![]() $\boldsymbol {k}$:
$\boldsymbol {k}$:
where ![]() $B_0 \equiv |\boldsymbol {B}_0|$,
$B_0 \equiv |\boldsymbol {B}_0|$, ![]() $k_{\|} \equiv \boldsymbol {k}\boldsymbol {\cdot } \hat {\boldsymbol {z}}$, and
$k_{\|} \equiv \boldsymbol {k}\boldsymbol {\cdot } \hat {\boldsymbol {z}}$, and ![]() $k_{\bot } \equiv |\boldsymbol {k}_{\perp }|$. In this notation,
$k_{\bot } \equiv |\boldsymbol {k}_{\perp }|$. In this notation, ![]() $\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}} + k_{\bot } \hat {\boldsymbol {x}}$. The conductivity tensor is then given by
$\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}} + k_{\bot } \hat {\boldsymbol {x}}$. The conductivity tensor is then given by
 \begin{align} \boldsymbol{\sigma} = \sum_s \boldsymbol{\sigma} _s & ={-} \frac{\mathrm{i}}{4 {\rm \pi}\omega} \sum_s \omega_{{\rm p}s}^2 \left[ \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}}{|k_{\|}|} \int_{-\infty}^{\infty} \mathrm{d} \tilde{w}_{s\|} \, \tilde{w}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varLambda_s(\tilde{w}_{s\|},\tilde{v}_{s\bot}) \hat{\boldsymbol{z}} \hat{\boldsymbol{z}}\right. \nonumber\\ &\quad \left.+ \,\tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{w}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \tilde{v}_{s\bot}^2 \varXi_s(\tilde{w}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{w}_{s\|}} \right] , \end{align}
\begin{align} \boldsymbol{\sigma} = \sum_s \boldsymbol{\sigma} _s & ={-} \frac{\mathrm{i}}{4 {\rm \pi}\omega} \sum_s \omega_{{\rm p}s}^2 \left[ \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}}{|k_{\|}|} \int_{-\infty}^{\infty} \mathrm{d} \tilde{w}_{s\|} \, \tilde{w}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varLambda_s(\tilde{w}_{s\|},\tilde{v}_{s\bot}) \hat{\boldsymbol{z}} \hat{\boldsymbol{z}}\right. \nonumber\\ &\quad \left.+ \,\tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{w}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \tilde{v}_{s\bot}^2 \varXi_s(\tilde{w}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{w}_{s\|}} \right] , \end{align}where
 $$\begin{gather} \omega_{{\rm p}s} \equiv \sqrt{\frac{4 {\rm \pi}Z_s^2 e^2 n_{s0}}{m_s}} , \end{gather}$$
$$\begin{gather} \omega_{{\rm p}s} \equiv \sqrt{\frac{4 {\rm \pi}Z_s^2 e^2 n_{s0}}{m_s}} , \end{gather}$$ $$\begin{gather}\varLambda_s(\tilde{w}_{s\|},\tilde{v}_{s\bot}) \equiv \tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{w}_{s\|}}-\tilde{w}_{s\|} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} , \end{gather}$$
$$\begin{gather}\varLambda_s(\tilde{w}_{s\|},\tilde{v}_{s\bot}) \equiv \tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{w}_{s\|}}-\tilde{w}_{s\|} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} , \end{gather}$$ $$\begin{gather}\varXi_s(\tilde{w}_{s\|},\tilde{v}_{s\bot}) \equiv \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} + \frac{\varLambda_s(\tilde{w}_{s\|},\tilde{v}_{s\bot})}{\tilde{\omega}_{s\|}} , \end{gather}$$
$$\begin{gather}\varXi_s(\tilde{w}_{s\|},\tilde{v}_{s\bot}) \equiv \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} + \frac{\varLambda_s(\tilde{w}_{s\|},\tilde{v}_{s\bot})}{\tilde{\omega}_{s\|}} , \end{gather}$$ $$\begin{align}(\boldsymbol{\mathsf{R}}_{sn} )_{zz} &\equiv \frac{\tilde{w}_{s\|}^2}{\tilde{v}_{s\bot}^2} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 . \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{R}}_{sn} )_{zz} &\equiv \frac{\tilde{w}_{s\|}^2}{\tilde{v}_{s\bot}^2} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 . \end{align}$$
Here, ![]() $(\boldsymbol{\mathsf{R}}_{sn})_{xy} = \hat {\boldsymbol {x}} \boldsymbol {\cdot } \boldsymbol{\mathsf{R}}_{sn} \boldsymbol {\cdot } \hat {\boldsymbol {y}}$, and similarly for other components of
$(\boldsymbol{\mathsf{R}}_{sn})_{xy} = \hat {\boldsymbol {x}} \boldsymbol {\cdot } \boldsymbol{\mathsf{R}}_{sn} \boldsymbol {\cdot } \hat {\boldsymbol {y}}$, and similarly for other components of ![]() $\boldsymbol{\mathsf{R}}_{sn}$. The integration in (2.77) is carried out over the Landau contour
$\boldsymbol{\mathsf{R}}_{sn}$. The integration in (2.77) is carried out over the Landau contour ![]() $C_L$; this is simply the real axis for growing perturbations, but has a more complicated form for non-growing ones (Landau Reference Landau1946; Schekochihin Reference Schekochihin2024). For the reader's convenience, a summary of the derivation of the hot-plasma dispersion relation is given in Appendix C.
$C_L$; this is simply the real axis for growing perturbations, but has a more complicated form for non-growing ones (Landau Reference Landau1946; Schekochihin Reference Schekochihin2024). For the reader's convenience, a summary of the derivation of the hot-plasma dispersion relation is given in Appendix C.
We note that the dielectric and conductivity tensors have the following symmetries:
where, for tensors with no species subscript, we use the notation ![]() $\mathfrak {E}_{xy} \equiv \hat {\boldsymbol {x}} \boldsymbol {\cdot } \boldsymbol {\mathfrak {E}} \boldsymbol {\cdot } \hat {\boldsymbol {y}}$. We also observe that if
$\mathfrak {E}_{xy} \equiv \hat {\boldsymbol {x}} \boldsymbol {\cdot } \boldsymbol {\mathfrak {E}} \boldsymbol {\cdot } \hat {\boldsymbol {y}}$. We also observe that if ![]() $f_{s0}(v_{\|},v_{\bot })$ is an even function with respect to
$f_{s0}(v_{\|},v_{\bot })$ is an even function with respect to ![]() $v_{\|}$, then, for
$v_{\|}$, then, for ![]() $k_{\|} > 0$,
$k_{\|} > 0$,
with the remaining components of the conductivity tensor given by (2.87a–c). If ![]() $f_{s0}(v_{\|},v_{\bot })$ is an odd function with respect to
$f_{s0}(v_{\|},v_{\bot })$ is an odd function with respect to ![]() $v_{\|}$, then
$v_{\|}$, then
These symmetries can be used to determine completely the behaviour of perturbations with ![]() $k_{\|} < 0$ directly from perturbations with
$k_{\|} < 0$ directly from perturbations with ![]() $k_{\|} > 0$, without any additional calculations. Thus, unless stated otherwise, from this point on, we assume
$k_{\|} > 0$, without any additional calculations. Thus, unless stated otherwise, from this point on, we assume ![]() $k_{\|} > 0$, and thus
$k_{\|} > 0$, and thus ![]() $\tilde {w}_{s\|} = \tilde {v}_{s\|}$ (see (2.79)).
$\tilde {w}_{s\|} = \tilde {v}_{s\|}$ (see (2.79)).
2.4.2. Simplifications of dispersion relation: overview of our approach
The full hot-plasma dispersion relation (2.75) is a transcendental equation, and thus, for general distribution functions, the growth rates of perturbations can only be determined numerically; this hinders the systematic investigation of stability over wide-ranging parameter regimes. However, adopting a few simplifications both to the form of the CE distribution functions (2.72) and to the type of microinstabilities being considered (see § 2.3.4) turns out to be advantageous when attempting a systematic study. It enables us to obtain simple analytical results for microinstability growth rates and characteristic wavenumbers, as well as greatly reducing the numerical cost of evaluating these quantities. The former allows us to make straightforward comparisons between microinstabilities, while the latter facilitates the calculation of stability plots over a wide range of parameters without requiring intensive computational resources.
First, we choose a Krook collision operator, with constant collision time ![]() $\tau _s$ for each species
$\tau _s$ for each species ![]() $s$ (Bhatnagar et al. Reference Bhatnagar, Gross and Krook1954), when evaluating the isotropic functions
$s$ (Bhatnagar et al. Reference Bhatnagar, Gross and Krook1954), when evaluating the isotropic functions ![]() $A_e^T(\tilde {v}_e)$,
$A_e^T(\tilde {v}_e)$, ![]() $A_e^R(\tilde {v}_e)$,
$A_e^R(\tilde {v}_e)$, ![]() $A_e^u(\tilde {v}_e)$,
$A_e^u(\tilde {v}_e)$, ![]() $A_i(\tilde {v}_i)$,
$A_i(\tilde {v}_i)$, ![]() $C_e(\tilde {v}_e)$ and
$C_e(\tilde {v}_e)$ and ![]() $C_i(\tilde {v}_i)$ in (2.72). As was explained in § 2.2.1, these functions are determined by the collision operator. While the full Landau collision operator might seem to be the most appropriate choice, the conductivity tensor
$C_i(\tilde {v}_i)$ in (2.72). As was explained in § 2.2.1, these functions are determined by the collision operator. While the full Landau collision operator might seem to be the most appropriate choice, the conductivity tensor ![]() $\boldsymbol {\sigma }$ defined by (2.77) cannot be written in terms of standard mathematical functions if this choice is made. Instead, the relevant integrals must be done numerically. If a simplified collision operator is assumed,
$\boldsymbol {\sigma }$ defined by (2.77) cannot be written in terms of standard mathematical functions if this choice is made. Instead, the relevant integrals must be done numerically. If a simplified collision operator is assumed, ![]() $\boldsymbol {\sigma }$ can be evaluated analytically with only a moderate amount of algebra. In Appendix B.2.1, we show that for the Krook collision operator
$\boldsymbol {\sigma }$ can be evaluated analytically with only a moderate amount of algebra. In Appendix B.2.1, we show that for the Krook collision operator
where it is assumed that ![]() $\tilde {v}_e, \tilde {v}_i \ll \eta _e^{-1/3}, \epsilon _i^{-1/2}$ in order that the CE distribution functions retain positive signs (the vanishing of the CE electron–ion-drift term is discussed in Appendix B.2.1). Adopting the Krook collision operator has the additional advantage of allowing a simple prescription for collisional damping of microinstabilities to be introduced self-consistently into our stability calculation (see § 2.5.7 for further discussion of this).
$\tilde {v}_e, \tilde {v}_i \ll \eta _e^{-1/3}, \epsilon _i^{-1/2}$ in order that the CE distribution functions retain positive signs (the vanishing of the CE electron–ion-drift term is discussed in Appendix B.2.1). Adopting the Krook collision operator has the additional advantage of allowing a simple prescription for collisional damping of microinstabilities to be introduced self-consistently into our stability calculation (see § 2.5.7 for further discussion of this).
Secondly, as discussed in § 2.3.4, the most important microinstabilities associated with the CE distribution function are low frequency, i.e. they satisfy (2.68). Therefore, instead of solving the full hot-plasma dispersion relation, we can obtain a less complicated algebraic dispersion relation. We also always consider electromagnetic rather than electrostatic perturbations. This is because it can be shown for a CE plasma that purely electrostatic microinstabilities are limited to the quasi-cold-plasma modes (see Appendix D). Describing how the simplified dispersion relation for low-frequency, electromagnetic perturbations is obtained from the full hot-plasma dispersion relation requires a rather lengthy exposition, and necessitates the introduction of a substantial amount of additional mathematical notation. In addition to this, certain shortcomings of this approach warrant an extended discussion. Readers who are interested these details will find them in the next section (§ 2.5). Readers who are instead keen to see the results of the stability calculations as soon as possible are encouraged to jump to §§ 3 and 4.
2.5. Linear stability calculation: detailed methodology
2.5.1. Low-frequency condition in a magnetised plasma
Before applying to the hot-plasma dispersion relation (2.75) the simplifications discussed in § 2.4.2, we refine the low-frequency condition (2.68) based on the specific form (2.77) of the conductivity tensor for a magnetised plasma. It is clear that the equilibrium distribution function only affects the conductivity tensor via the functions ![]() $\varLambda _s(\tilde {v}_{s\|},\tilde {v}_{s\bot })$ and
$\varLambda _s(\tilde {v}_{s\|},\tilde {v}_{s\bot })$ and ![]() $\varXi _s(\tilde {v}_{s\|},\tilde {v}_{s\bot })$ (see (2.84) and (2.85)). For a distribution function of the form (2.72), it can be shown that
$\varXi _s(\tilde {v}_{s\|},\tilde {v}_{s\bot })$ (see (2.84) and (2.85)). For a distribution function of the form (2.72), it can be shown that
and
 \begin{align} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) & ={-} \tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \left[ 2 + 2 \tilde{v}_{s\|} \eta_s A_s(\tilde{v}_s) - \frac{\tilde{v}_{s\|}}{\tilde{v}_s} \eta_s A_s'(\tilde{v}_s)\right. \nonumber\\ & \quad + 2 \epsilon_s C_s(\tilde{v}_s) \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}+\frac{1}{2}\right) - \frac{1}{\tilde{v}_s} \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}\right) \epsilon_s C_s'(\tilde{v}_s) \nonumber\\ &\left.\quad +\, \frac{\eta_s}{ \tilde{\omega}_{s\|}} A_s(\tilde{v}_s) - 3 \frac{\epsilon_s}{ \tilde{\omega}_{s\|}} C_s(\tilde{v}_s) \tilde{v}_{s\|} \right] , \end{align}
\begin{align} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) & ={-} \tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \left[ 2 + 2 \tilde{v}_{s\|} \eta_s A_s(\tilde{v}_s) - \frac{\tilde{v}_{s\|}}{\tilde{v}_s} \eta_s A_s'(\tilde{v}_s)\right. \nonumber\\ & \quad + 2 \epsilon_s C_s(\tilde{v}_s) \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}+\frac{1}{2}\right) - \frac{1}{\tilde{v}_s} \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}\right) \epsilon_s C_s'(\tilde{v}_s) \nonumber\\ &\left.\quad +\, \frac{\eta_s}{ \tilde{\omega}_{s\|}} A_s(\tilde{v}_s) - 3 \frac{\epsilon_s}{ \tilde{\omega}_{s\|}} C_s(\tilde{v}_s) \tilde{v}_{s\|} \right] , \end{align}
where the first term in the square brackets in (2.93) originates from the Maxwellian part of the distribution function. A comparison of the size of the second, third, fourth and fifth terms with the first indicates that for ![]() $\tilde {v}_s \sim 1$ – for which
$\tilde {v}_s \sim 1$ – for which ![]() $\varXi _s$ attains its largest characteristic values – the non-Maxwellian terms of the CE distribution function only provide a small,
$\varXi _s$ attains its largest characteristic values – the non-Maxwellian terms of the CE distribution function only provide a small, ![]() ${O}(\eta _e, \epsilon _e)$ contribution, and thus the conductivity is only altered slightly. However, considering the sixth and seventh terms in the square brackets in (2.93) (which are only present thanks to the anisotropy of the CE distribution function), it is clear that the non-Maxwellian contribution to the conductivity tensor can be significant for
${O}(\eta _e, \epsilon _e)$ contribution, and thus the conductivity is only altered slightly. However, considering the sixth and seventh terms in the square brackets in (2.93) (which are only present thanks to the anisotropy of the CE distribution function), it is clear that the non-Maxwellian contribution to the conductivity tensor can be significant for ![]() $\tilde {v}_s \sim 1$ provided the frequency (2.81) satisfies one of
$\tilde {v}_s \sim 1$ provided the frequency (2.81) satisfies one of
Thus, the relevant low-frequency condition in a magnetised plasma involves the parallel particle streaming rate ![]() $k_{\|} v_{\mathrm {th}s}$.
$k_{\|} v_{\mathrm {th}s}$.
There do exist certain caveats to the claim that it is necessary for microinstabilities of CE plasma to satisfy (2.94); we defer detailed statement and discussion of these caveats – as well as of other potential shortcomings of our approach – to §§ 2.5.6, 2.5.7 and 2.5.8.
2.5.2. Simplification I: non-relativistic electromagnetic fluctuations
The requirement that the mode be electromagnetic, combined with the fact we are interested in non-relativistic fluctuations (![]() $\omega \ll k c$) enables our first simplification. We see from (2.75) that for any perturbation of interest, the dielectric tensor must satisfy
$\omega \ll k c$) enables our first simplification. We see from (2.75) that for any perturbation of interest, the dielectric tensor must satisfy ![]() $\|\boldsymbol {\mathfrak {E}}\| \gtrsim k^2 c^2/\omega ^2 \gg 1$ (where
$\|\boldsymbol {\mathfrak {E}}\| \gtrsim k^2 c^2/\omega ^2 \gg 1$ (where ![]() $\| \cdot \|$ is the Euclidean tensor norm); therefore, it simplifies to
$\| \cdot \|$ is the Euclidean tensor norm); therefore, it simplifies to
This amounts to ignoring the displacement current in the Ampère–Maxwell law, leaving Ampère's original equation. For convenience of exposition, we denote the contribution of each species ![]() $s$ to (2.95) by
$s$ to (2.95) by
2.5.3. Simplification II: expansion of dielectric tensor in  $\omega \ll k_{\|} v_{\mathrm {th}s}$
$\omega \ll k_{\|} v_{\mathrm {th}s}$
The next simplification involves an expansion of the matrices ![]() $\boldsymbol {\mathfrak {E}}_s$ in the small parameters
$\boldsymbol {\mathfrak {E}}_s$ in the small parameters ![]() $\tilde {\omega }_{s\|} \sim \eta _s \sim \epsilon _s \ll 1$. The general principle of the expansion is as follows. We first divide the matrix
$\tilde {\omega }_{s\|} \sim \eta _s \sim \epsilon _s \ll 1$. The general principle of the expansion is as follows. We first divide the matrix ![]() $\boldsymbol {\mathfrak {E}}_s$ (see (2.74), (2.77) and (2.96)) into the Maxwellian contribution
$\boldsymbol {\mathfrak {E}}_s$ (see (2.74), (2.77) and (2.96)) into the Maxwellian contribution ![]() $\boldsymbol{\mathsf{M}}_s$ and the non-Maxwellian one
$\boldsymbol{\mathsf{M}}_s$ and the non-Maxwellian one ![]() $\boldsymbol{\mathsf{P}}_s$:
$\boldsymbol{\mathsf{P}}_s$:
where the ![]() $\omega _{{\rm p}s}^2/\omega ^2$ factor is introduced for later convenience. Next, we note that, for a Maxwellian distribution,
$\omega _{{\rm p}s}^2/\omega ^2$ factor is introduced for later convenience. Next, we note that, for a Maxwellian distribution, ![]() $\varLambda _s(\tilde {v}_{s\|},\tilde {v}_{s\bot }) = 0$ (see (2.84)), whereas
$\varLambda _s(\tilde {v}_{s\|},\tilde {v}_{s\bot }) = 0$ (see (2.84)), whereas ![]() $\varLambda _s \sim \epsilon _{s}, \eta _s$ for the non-Maxwellian component of the CE distribution function. Thus, from (2.77) considered under the ordering
$\varLambda _s \sim \epsilon _{s}, \eta _s$ for the non-Maxwellian component of the CE distribution function. Thus, from (2.77) considered under the ordering ![]() $k \rho _s \sim 1$,
$k \rho _s \sim 1$, ![]() $\boldsymbol{\mathsf{M}}_s = {O}(\tilde {\omega }_{s\|})$ as
$\boldsymbol{\mathsf{M}}_s = {O}(\tilde {\omega }_{s\|})$ as ![]() $\tilde {\omega }_{s\|} \rightarrow 0$, while
$\tilde {\omega }_{s\|} \rightarrow 0$, while ![]() $\boldsymbol{\mathsf{P}}_s = {O}(\eta _s, \epsilon _s)$. The expansion of
$\boldsymbol{\mathsf{P}}_s = {O}(\eta _s, \epsilon _s)$. The expansion of ![]() $\boldsymbol{\mathsf{M}}_s$ and
$\boldsymbol{\mathsf{M}}_s$ and ![]() $\boldsymbol{\mathsf{P}}_s$ in
$\boldsymbol{\mathsf{P}}_s$ in ![]() $\tilde {\omega }_{s\|}$ is, therefore,
$\tilde {\omega }_{s\|}$ is, therefore,
where the matrices ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ and
$\boldsymbol{\mathsf{M}}_s^{(0)}$ and ![]() $\boldsymbol{\mathsf{M}}_s^{(1)}$ are
$\boldsymbol{\mathsf{M}}_s^{(1)}$ are ![]() ${O}(1)$ functions of
${O}(1)$ functions of ![]() $\boldsymbol {k}$ only, and
$\boldsymbol {k}$ only, and ![]() $\boldsymbol{\mathsf{P}}_s^{(0)}$ and
$\boldsymbol{\mathsf{P}}_s^{(0)}$ and ![]() $\boldsymbol{\mathsf{P}}_s^{(1)}$ are
$\boldsymbol{\mathsf{P}}_s^{(1)}$ are ![]() ${O}(\eta _s, \epsilon _s)$. We then expand
${O}(\eta _s, \epsilon _s)$. We then expand ![]() $\boldsymbol {\mathfrak {E}}_s$ as follows:
$\boldsymbol {\mathfrak {E}}_s$ as follows:
where
2.5.4. Additional symmetries of low-frequency dielectric tensor  ${\mathfrak{E}}$
${\mathfrak{E}}$ $_s^{(0)}$
$_s^{(0)}$
The tensor ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$ defined by (2.100a) has some rather convenient additional symmetries, which lead to significant simplification of the dispersion relation. In Appendix F we show that in combination with the general symmetries (2.87a–c), which apply to
$\boldsymbol {\mathfrak {E}}_s^{(0)}$ defined by (2.100a) has some rather convenient additional symmetries, which lead to significant simplification of the dispersion relation. In Appendix F we show that in combination with the general symmetries (2.87a–c), which apply to ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$ in addition to
$\boldsymbol {\mathfrak {E}}_s^{(0)}$ in addition to ![]() $\boldsymbol {\mathfrak {E}}$, for any distribution function of particle species
$\boldsymbol {\mathfrak {E}}$, for any distribution function of particle species ![]() $s$ with a small anisotropy:
$s$ with a small anisotropy:
 $$\begin{gather}(\boldsymbol{\mathfrak{E}}_s^{(0)})_{zz} = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} . \end{gather}$$
$$\begin{gather}(\boldsymbol{\mathfrak{E}}_s^{(0)})_{zz} = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} . \end{gather}$$These symmetries have the consequence that
As a result of this identity, it is convenient to calculate the components of ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$ (and
$\boldsymbol {\mathfrak {E}}_s^{(0)}$ (and ![]() $\boldsymbol {\mathfrak {E}}_s$) in the coordinate basis
$\boldsymbol {\mathfrak {E}}_s$) in the coordinate basis ![]() $\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$ defined by
$\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$ defined by
Carrying out this calculation (see Appendix F), we find
 $$\begin{align} &(\boldsymbol{\mathfrak{E}}_s^{(0)})_{11} = \frac{k^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} , \end{align}$$
$$\begin{align} &(\boldsymbol{\mathfrak{E}}_s^{(0)})_{11} = \frac{k^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} , \end{align}$$
where ![]() $(\boldsymbol {\mathfrak {E}}_s^{(0)})_{ij}$ is the
$(\boldsymbol {\mathfrak {E}}_s^{(0)})_{ij}$ is the ![]() $(i,j)$th component of
$(i,j)$th component of ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$ in the basis
$\boldsymbol {\mathfrak {E}}_s^{(0)}$ in the basis ![]() $\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3 \}$. We conclude that, if
$\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3 \}$. We conclude that, if ![]() $k \rho _s \sim 1$ and
$k \rho _s \sim 1$ and ![]() $\tilde {\omega }_{s\|} \ll 1$, the components of
$\tilde {\omega }_{s\|} \ll 1$, the components of ![]() $\boldsymbol {\mathfrak {E}}_s$ satisfy
$\boldsymbol {\mathfrak {E}}_s$ satisfy
These components can be written in terms of the components of ![]() $\boldsymbol {\mathfrak {E}}_s$ in the
$\boldsymbol {\mathfrak {E}}_s$ in the ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ coordinate frame (see (2.76a–c)) via a coordinate transformation; the resulting expressions are rather bulky, so we do not reproduce them here – they are detailed in Appendix G.
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ coordinate frame (see (2.76a–c)) via a coordinate transformation; the resulting expressions are rather bulky, so we do not reproduce them here – they are detailed in Appendix G.
2.5.5. Consequences for dispersion relation
On account of the additional symmetries described in the previous section, a simplified dispersion relation for low-frequency modes can be derived in place of the full hot-plasma dispersion relation (2.75). However, depending on the frequency and characteristic wavelengths of modes, this derivation has a subtlety because of the large discrepancy between ion and electron masses. In, e.g. a two-species plasma with ![]() $\mu _e = m_e/m_i \ll 1$ (and ion charge
$\mu _e = m_e/m_i \ll 1$ (and ion charge ![]() $Z_i$), we have
$Z_i$), we have
where ![]() $\tau = T_i/T_e$. If
$\tau = T_i/T_e$. If ![]() $\tau \sim 1$ (as would be expected in a collisional plasma on macroscopic evolution time scales
$\tau \sim 1$ (as would be expected in a collisional plasma on macroscopic evolution time scales ![]() $\tau _L$ greater than the ion–electron temperature-equilibration time
$\tau _L$ greater than the ion–electron temperature-equilibration time ![]() $\tau _{ie}^{\rm eq}$ – cf. (2.54)), then
$\tau _{ie}^{\rm eq}$ – cf. (2.54)), then ![]() $\tilde {\omega }_{i\|} \sim {\mu _e}^{-1/2} \tilde {\omega }_{e\|} \gg \tilde {\omega }_{e\|}$. Thus, in general,
$\tilde {\omega }_{i\|} \sim {\mu _e}^{-1/2} \tilde {\omega }_{e\|} \gg \tilde {\omega }_{e\|}$. Thus, in general, ![]() $\tilde {\omega }_{i\|} \not \sim \tilde {\omega }_{e\|}$, and any dispersion relation will, in principle, depend on an additional (small) dimensionless parameter
$\tilde {\omega }_{i\|} \not \sim \tilde {\omega }_{e\|}$, and any dispersion relation will, in principle, depend on an additional (small) dimensionless parameter ![]() $\mu _e$. This introduces various complications to the simplified dispersion relation's derivation, most significant of which being that, since
$\mu _e$. This introduces various complications to the simplified dispersion relation's derivation, most significant of which being that, since ![]() $\rho _e = Z_i \mu _e^{1/2} \tau ^{-1/2} \rho _i \ll \rho _i$ (for
$\rho _e = Z_i \mu _e^{1/2} \tau ^{-1/2} \rho _i \ll \rho _i$ (for ![]() $Z_i \gtrsim 1$), to assume the ordering
$Z_i \gtrsim 1$), to assume the ordering ![]() $k \rho _s \sim 1$ for both ions and electrons is inconsistent (see § 2.5.6).
$k \rho _s \sim 1$ for both ions and electrons is inconsistent (see § 2.5.6).
To avoid the description of our approach being obscured by these complications, we consider a special case at first: we adopt the ordering ![]() $k \rho _e \sim 1$ in a two-species plasma and assume that
$k \rho _e \sim 1$ in a two-species plasma and assume that ![]() $\tilde {\omega }_{i\|} \sim \mu _e^{-1/2} \tilde {\omega }_{e\|} \ll 1$. In this case,
$\tilde {\omega }_{i\|} \sim \mu _e^{-1/2} \tilde {\omega }_{e\|} \ll 1$. In this case, ![]() $\tilde {\omega }_{i\|} \|\boldsymbol {\mathfrak {E}}_i^{(0)}\| \sim \mu _e^{1/2} Z_i \tau ^{-1/2} \tilde {\omega }_{e\|} \|\boldsymbol {\mathfrak {E}}_e^{(0)}\| \ll \tilde {\omega }_{e\|} \|\boldsymbol {\mathfrak {E}}_e^{(0)}\|$, and so the dielectric tensor
$\tilde {\omega }_{i\|} \|\boldsymbol {\mathfrak {E}}_i^{(0)}\| \sim \mu _e^{1/2} Z_i \tau ^{-1/2} \tilde {\omega }_{e\|} \|\boldsymbol {\mathfrak {E}}_e^{(0)}\| \ll \tilde {\omega }_{e\|} \|\boldsymbol {\mathfrak {E}}_e^{(0)}\|$, and so the dielectric tensor ![]() $\boldsymbol {\mathfrak {E}}$ is given by
$\boldsymbol {\mathfrak {E}}$ is given by
where
 $$\begin{align}\boldsymbol{\mathfrak{E}}^{(1)} &\equiv \boldsymbol{\mathfrak{E}}_e^{(1)} + \frac{\tilde{\omega}_{i\|}^2}{\tilde{\omega}_{e\|}^2} \boldsymbol{\mathfrak{E}}_i^{(1)} . \end{align}$$
$$\begin{align}\boldsymbol{\mathfrak{E}}^{(1)} &\equiv \boldsymbol{\mathfrak{E}}_e^{(1)} + \frac{\tilde{\omega}_{i\|}^2}{\tilde{\omega}_{e\|}^2} \boldsymbol{\mathfrak{E}}_i^{(1)} . \end{align}$$
Thus, to leading order in the ![]() $\tilde {\omega }_{e\|} \ll 1$ expansion, only the electron species contributes to the dielectric tensor for electron-Larmor-scale modes. We revisit the derivation of simplified dispersion relations for CE microinstabilities more generally in § 2.5.6.
$\tilde {\omega }_{e\|} \ll 1$ expansion, only the electron species contributes to the dielectric tensor for electron-Larmor-scale modes. We revisit the derivation of simplified dispersion relations for CE microinstabilities more generally in § 2.5.6.
To derive the simplified dispersion relation for electron-Larmor-scale modes, we start by considering the component of (2.73) for the electric field that is parallel to the wavevector ![]() $\hat {\boldsymbol {k}}$,
$\hat {\boldsymbol {k}}$,
and then substitute the expanded form (2.107) of the dielectric tensor (with ![]() $s = e$). The orthogonality of
$s = e$). The orthogonality of ![]() $\boldsymbol {\mathfrak {E}}_e^{(0)}$ to
$\boldsymbol {\mathfrak {E}}_e^{(0)}$ to ![]() $\hat {\boldsymbol {k}}$ – viz. (2.102) – implies that (2.109) becomes
$\hat {\boldsymbol {k}}$ – viz. (2.102) – implies that (2.109) becomes
where the transverse electric field is defined by ![]() $\widehat {\delta \boldsymbol {E}}_{T} \equiv \widehat {\delta \boldsymbol {E}} \boldsymbol {\cdot } (\boldsymbol{\mathsf{I}} - \hat {\boldsymbol {k}} \hat {\boldsymbol {k}} )$. In Appendix D.2, we show that for
$\widehat {\delta \boldsymbol {E}}_{T} \equiv \widehat {\delta \boldsymbol {E}} \boldsymbol {\cdot } (\boldsymbol{\mathsf{I}} - \hat {\boldsymbol {k}} \hat {\boldsymbol {k}} )$. In Appendix D.2, we show that for ![]() $\tilde {\omega }_{e\|}, \tilde {\omega }_{i\|} \ll 1$,
$\tilde {\omega }_{e\|}, \tilde {\omega }_{i\|} \ll 1$,
Since this is strictly positive, we can rewrite (2.110) to give the electrostatic field in terms of the transverse electric field:
We conclude that ![]() $|\hat {\boldsymbol {k}} \boldsymbol {\cdot } \widehat {\delta \boldsymbol {E}}| \sim |\widehat {\delta \boldsymbol {E}}_T|$ for all low-frequency perturbations with
$|\hat {\boldsymbol {k}} \boldsymbol {\cdot } \widehat {\delta \boldsymbol {E}}| \sim |\widehat {\delta \boldsymbol {E}}_T|$ for all low-frequency perturbations with ![]() $k_{\|} \sim k$; a corollary of this result is that there can be no low-frequency purely electrostatic perturbations (see Appendix D.4.1 for an alternative demonstration of this).
$k_{\|} \sim k$; a corollary of this result is that there can be no low-frequency purely electrostatic perturbations (see Appendix D.4.1 for an alternative demonstration of this).
We can now derive the dispersion relation from the other two components of (2.73),
by (again) substituting the expanded dielectric tensor (2.107) into (2.113):
where we have used the identity
and ordered ![]() $k^2 c^2/\omega ^2 \sim \tilde {\omega }_{e\|} \|\boldsymbol {\mathfrak {E}}^{(0)}\|$. The ratio of the right-hand side of (2.114) to the left-hand side is
$k^2 c^2/\omega ^2 \sim \tilde {\omega }_{e\|} \|\boldsymbol {\mathfrak {E}}^{(0)}\|$. The ratio of the right-hand side of (2.114) to the left-hand side is ![]() ${O}(\tilde {\omega }_{e\|})$; we thus conclude that, to leading order in the
${O}(\tilde {\omega }_{e\|})$; we thus conclude that, to leading order in the ![]() $\tilde {\omega }_{e\|} \ll 1$ expansion,
$\tilde {\omega }_{e\|} \ll 1$ expansion,
and the dispersion relation is approximately
Finally, writing the dielectric tensor in terms of ![]() $\boldsymbol{\mathsf{M}}_{e}$ and
$\boldsymbol{\mathsf{M}}_{e}$ and ![]() $\boldsymbol{\mathsf{P}}_{e}$ as defined by (2.97), we find
$\boldsymbol{\mathsf{P}}_{e}$ as defined by (2.97), we find
 \begin{align}
&\left[\tilde{\omega}_{e\|}
(\boldsymbol{\mathsf{M}}_{e}^{(0)})_{11} +
(\boldsymbol{\mathsf{P}}_{e}^{(0)})_{11}- k^2
d_e^2\right]\left[\tilde{\omega}_{e\|}
(\boldsymbol{\mathsf{M}}_{e}^{(0)})_{22} +
(\boldsymbol{\mathsf{P}}_{e}^{(0)})_{22} - k^2
d_e^2\right] \nonumber\\ & + \left[\tilde{\omega}_{e\|}
(\boldsymbol{\mathsf{M}}_{e}^{(0)})_{12} +
(\boldsymbol{\mathsf{P}}_{e}^{(0)})_{12}\right]^2 = 0
, \end{align}
\begin{align}
&\left[\tilde{\omega}_{e\|}
(\boldsymbol{\mathsf{M}}_{e}^{(0)})_{11} +
(\boldsymbol{\mathsf{P}}_{e}^{(0)})_{11}- k^2
d_e^2\right]\left[\tilde{\omega}_{e\|}
(\boldsymbol{\mathsf{M}}_{e}^{(0)})_{22} +
(\boldsymbol{\mathsf{P}}_{e}^{(0)})_{22} - k^2
d_e^2\right] \nonumber\\ & + \left[\tilde{\omega}_{e\|}
(\boldsymbol{\mathsf{M}}_{e}^{(0)})_{12} +
(\boldsymbol{\mathsf{P}}_{e}^{(0)})_{12}\right]^2 = 0
, \end{align}
where ![]() $d_e = c/\omega _{{\rm p}e}$ is the electron inertial scale (see (2.58b)). This can be re-written as a quadratic equation in
$d_e = c/\omega _{{\rm p}e}$ is the electron inertial scale (see (2.58b)). This can be re-written as a quadratic equation in ![]() $\omega$ – and thus, expressions for the complex frequency of any low-frequency perturbation can be found for any given positive wavenumber. We note that the electron inertial scale is related to the electron-Larmor radius by
$\omega$ – and thus, expressions for the complex frequency of any low-frequency perturbation can be found for any given positive wavenumber. We note that the electron inertial scale is related to the electron-Larmor radius by ![]() $d_e = \rho _e \beta _e^{-1/2}$; therefore, our expansion scheme is only consistent with the low-frequency assumption (2.94) under our assumed ordering,
$d_e = \rho _e \beta _e^{-1/2}$; therefore, our expansion scheme is only consistent with the low-frequency assumption (2.94) under our assumed ordering, ![]() $\tilde {\omega }_{e\|} \sim \beta _e^{-1}$, when
$\tilde {\omega }_{e\|} \sim \beta _e^{-1}$, when ![]() $\beta _e \gg 1$.
$\beta _e \gg 1$.
We note that one only needs to know ![]() $\boldsymbol {\mathfrak {E}}_e^{(0)}$ in order to obtain the dispersion relation of low-frequency perturbations and the transverse component of the electric field, whereas to determine the electrostatic component of the electric field (and other quantities, such as the density perturbation – see Appendix H), one must go to higher order in the
$\boldsymbol {\mathfrak {E}}_e^{(0)}$ in order to obtain the dispersion relation of low-frequency perturbations and the transverse component of the electric field, whereas to determine the electrostatic component of the electric field (and other quantities, such as the density perturbation – see Appendix H), one must go to higher order in the ![]() $\tilde {\omega }_{e\|} \ll 1$ expansion. Since we are primarily interested in microinstability growth rates and wavenumber scales, we will not explicitly calculate the electrostatic fields associated with perturbations using (2.112), and thus can avoid the rather laborious calculation of
$\tilde {\omega }_{e\|} \ll 1$ expansion. Since we are primarily interested in microinstability growth rates and wavenumber scales, we will not explicitly calculate the electrostatic fields associated with perturbations using (2.112), and thus can avoid the rather laborious calculation of ![]() $\boldsymbol {\mathfrak {E}}^{(1)}$ for CE distribution functions. We do, however, in Appendix G.1.3 derive an explicit expression for
$\boldsymbol {\mathfrak {E}}^{(1)}$ for CE distribution functions. We do, however, in Appendix G.1.3 derive an explicit expression for ![]() $\boldsymbol {\mathfrak {E}}^{(1)}$ for a plasma with Maxwellian distribution functions for all particle species; this in turn allows us to relate the electrostatic electric field to the transverse field for such a plasma (see Appendix I).
$\boldsymbol {\mathfrak {E}}^{(1)}$ for a plasma with Maxwellian distribution functions for all particle species; this in turn allows us to relate the electrostatic electric field to the transverse field for such a plasma (see Appendix I).
For the sake of completeness, we also observe that if the non-Maxwellian part of the CE distribution function is even with respect to ![]() $v_{\|}$, the transformation rules (2.89) combined with (2.104) imply that a perturbation with a negative parallel wavenumber
$v_{\|}$, the transformation rules (2.89) combined with (2.104) imply that a perturbation with a negative parallel wavenumber ![]() $k_{\|}$ will obey exactly the same dispersion relation as a perturbation for a positive parallel wavenumber, viz. for
$k_{\|}$ will obey exactly the same dispersion relation as a perturbation for a positive parallel wavenumber, viz. for ![]() $k_{\|} > 0$,
$k_{\|} > 0$,
If instead the non-Maxwellian part is odd, then, for ![]() $k_{\|} > 0$,
$k_{\|} > 0$,
The dispersion relation for perturbations with ![]() $k_{\|} < 0$ can, therefore, be recovered by considering perturbations with
$k_{\|} < 0$ can, therefore, be recovered by considering perturbations with ![]() $k_{\|} > 0$, but under the substitution
$k_{\|} > 0$, but under the substitution ![]() $\boldsymbol{\mathsf{P}}_{e}^{(0)} \rightarrow -\boldsymbol{\mathsf{P}}_{e}^{(0)}$. Thus, we can characterise all unstable perturbations under the assumption that
$\boldsymbol{\mathsf{P}}_{e}^{(0)} \rightarrow -\boldsymbol{\mathsf{P}}_{e}^{(0)}$. Thus, we can characterise all unstable perturbations under the assumption that ![]() $k_{\|} > 0$.
$k_{\|} > 0$.
In all subsequent calculations, we require the Maxwellian part ![]() $\boldsymbol{\mathsf{M}}_e^{(0)}$ of the dielectric tensor. The elements of the matrix
$\boldsymbol{\mathsf{M}}_e^{(0)}$ of the dielectric tensor. The elements of the matrix ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ of species
$\boldsymbol{\mathsf{M}}_s^{(0)}$ of species ![]() $s$ are as follows:
$s$ are as follows:
 $$\begin{align} (\boldsymbol{\mathsf{M}}_{s}^{(0)})_{11} &= \mathrm{i} \frac{k^2}{k_{\|}^2} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_{s}^{(0)})_{11} &= \mathrm{i} \frac{k^2}{k_{\|}^2} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}$$
where the functions ![]() $F(x,y)$,
$F(x,y)$, ![]() $G(x,y)$ and
$G(x,y)$ and ![]() $H(x,y)$ are
$H(x,y)$ are
 $$\begin{align} F\!\left(x,y\right) &\equiv \frac{4 \sqrt{\rm \pi}}{y^2} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m=1}^{\infty} m^2 {I}_{m}\!\left(\frac{y^2}{2}\right)\exp{\left(-\frac{m^2}{x^2}\right)} , \end{align}$$
$$\begin{align} F\!\left(x,y\right) &\equiv \frac{4 \sqrt{\rm \pi}}{y^2} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m=1}^{\infty} m^2 {I}_{m}\!\left(\frac{y^2}{2}\right)\exp{\left(-\frac{m^2}{x^2}\right)} , \end{align}$$ $$\begin{align}G\!\left(x,y\right) &\equiv \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} m \, {\rm Re}\,{Z\!\left(\frac{m}{x}\right)} \left[ {I}_{m}'\!\left(\frac{y^2}{2}\right)- {I}_{m}\! \left(\frac{y^2}{2}\right)\right] , \end{align}$$
$$\begin{align}G\!\left(x,y\right) &\equiv \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} m \, {\rm Re}\,{Z\!\left(\frac{m}{x}\right)} \left[ {I}_{m}'\!\left(\frac{y^2}{2}\right)- {I}_{m}\! \left(\frac{y^2}{2}\right)\right] , \end{align}$$ $$\begin{align}H\!\left(x,y\right) &\equiv F\!\left(x,y\right) + \sqrt{\rm \pi} y^2 \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} \left[ {I}_{m}\!\left(\frac{y^2}{2}\right)- {I}_{m}'\!\left(\frac{y^2}{2}\right)\right] \exp{\left(-\frac{m^2}{x^2}\right)} , \end{align}$$
$$\begin{align}H\!\left(x,y\right) &\equiv F\!\left(x,y\right) + \sqrt{\rm \pi} y^2 \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} \left[ {I}_{m}\!\left(\frac{y^2}{2}\right)- {I}_{m}'\!\left(\frac{y^2}{2}\right)\right] \exp{\left(-\frac{m^2}{x^2}\right)} , \end{align}$$
where ![]() ${I}_{m}(\alpha )$ is the
${I}_{m}(\alpha )$ is the ![]() $m$th modified Bessel function, and
$m$th modified Bessel function, and
is the plasma dispersion function (Fried & Conte Reference Fried and Conte1961). The derivation of these results from the full dielectric tensor (which is calculated in Appendix G.1.1) for a plasma whose constituent particles all have Maxwellian distributions is presented in Appendices G.1.2 (expansion in the ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ basis) and G.1.3 (expansion in the
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ basis) and G.1.3 (expansion in the ![]() $\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3 \}$ basis).
$\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3 \}$ basis).
2.5.6. Effect of multiple species on dispersion-relation derivations
We now relax the assumptions adopted in § 2.5.5 that the low-frequency modes of interest are on electron-Larmor scales, and discuss how we derive simplified dispersion relations for (low-frequency) CE microinstabilities more generally.
First, it is unnecessarily restrictive to assume that, for all CE microinstabilities, ![]() $\tilde {\omega }_{s\|} \ll 1$ for all particle species. There are some instabilities for which
$\tilde {\omega }_{s\|} \ll 1$ for all particle species. There are some instabilities for which ![]() $\tilde {\omega }_{e\|} \sim \eta _e \sim \epsilon _e \ll 1$ while
$\tilde {\omega }_{e\|} \sim \eta _e \sim \epsilon _e \ll 1$ while ![]() $\tilde {\omega }_{i\|} \gtrsim 1$. Recalling the orderings
$\tilde {\omega }_{i\|} \gtrsim 1$. Recalling the orderings ![]() $\tilde {\omega }_{e\|} \sim \beta _e^{-1}$ and
$\tilde {\omega }_{e\|} \sim \beta _e^{-1}$ and ![]() $k \rho _e \sim 1$ that were adopted for the electron-Larmor-scale instabilities described in § 2.5.5, it follows that
$k \rho _e \sim 1$ that were adopted for the electron-Larmor-scale instabilities described in § 2.5.5, it follows that ![]() $\tilde {\omega }_{i\|} \gtrsim 1$ whenever
$\tilde {\omega }_{i\|} \gtrsim 1$ whenever ![]() $\beta _e \lesssim \tau ^{-1/2} \mu _e^{-1/2}$; in other words, electron-Larmor-scale CE microinstabilities in plasmas with
$\beta _e \lesssim \tau ^{-1/2} \mu _e^{-1/2}$; in other words, electron-Larmor-scale CE microinstabilities in plasmas with ![]() $\beta _e$ that is not too large will satisfy
$\beta _e$ that is not too large will satisfy ![]() $\tilde {\omega }_{i\|} \gtrsim 1$. Therefore, we cannot naively apply our low-frequency approximation to both
$\tilde {\omega }_{i\|} \gtrsim 1$. Therefore, we cannot naively apply our low-frequency approximation to both ![]() $\boldsymbol {\mathfrak {E}}_e$ and
$\boldsymbol {\mathfrak {E}}_e$ and ![]() $\boldsymbol {\mathfrak {E}}_i$ in all cases of interest. We will remain cognisant of this in the calculations that follow – a concrete example of
$\boldsymbol {\mathfrak {E}}_i$ in all cases of interest. We will remain cognisant of this in the calculations that follow – a concrete example of ![]() $\tilde {\omega }_{i\|} \gtrsim 1$ will be considered in § 3.3.1.
$\tilde {\omega }_{i\|} \gtrsim 1$ will be considered in § 3.3.1.
Secondly, because of the large separation between electron- and ion-Larmor scales, it is necessary to consider whether the approximation ![]() $\boldsymbol{\mathsf{M}}_s(\tilde {\omega }_{s\|},\boldsymbol {k}) \approx \tilde {\omega }_{s\|} \boldsymbol{\mathsf{M}}_s^{(0)}(\boldsymbol {k})$ remains valid for parallel or perpendicular wavenumbers much larger or smaller than the inverse Larmor radii of each species. We show in Appendix G.1.6 that the leading-order term in the
$\boldsymbol{\mathsf{M}}_s(\tilde {\omega }_{s\|},\boldsymbol {k}) \approx \tilde {\omega }_{s\|} \boldsymbol{\mathsf{M}}_s^{(0)}(\boldsymbol {k})$ remains valid for parallel or perpendicular wavenumbers much larger or smaller than the inverse Larmor radii of each species. We show in Appendix G.1.6 that the leading-order term in the ![]() $\tilde {\omega }_{s\|} \ll 1$ expansion remains larger than higher-order terms for all
$\tilde {\omega }_{s\|} \ll 1$ expansion remains larger than higher-order terms for all ![]() $k_{\|} \rho _s \gtrsim 1$ (as, indeed, was implicitly assumed in § 2.5.5). However, for
$k_{\|} \rho _s \gtrsim 1$ (as, indeed, was implicitly assumed in § 2.5.5). However, for ![]() $k_{\|} \rho _s$ sufficiently small, the same statement does not hold for all components of
$k_{\|} \rho _s$ sufficiently small, the same statement does not hold for all components of ![]() $\boldsymbol{\mathsf{M}}_s$. More specifically, it is shown in the same appendix that the dominant contribution to
$\boldsymbol{\mathsf{M}}_s$. More specifically, it is shown in the same appendix that the dominant contribution to ![]() $\boldsymbol{\mathsf{M}}_s(\boldsymbol {k})$ when
$\boldsymbol{\mathsf{M}}_s(\boldsymbol {k})$ when ![]() $k_{\|} \rho _s \ll 1$ instead comes from the quadratic term
$k_{\|} \rho _s \ll 1$ instead comes from the quadratic term ![]() $\tilde {\omega }_{s\|}^2 \boldsymbol{\mathsf{M}}_s^{(1)}(\boldsymbol {k})$ (rather than any higher-order term). Thus, in general, our simplified dispersion relation for low-frequency modes in a two-species plasma has the form of a quartic in
$\tilde {\omega }_{s\|}^2 \boldsymbol{\mathsf{M}}_s^{(1)}(\boldsymbol {k})$ (rather than any higher-order term). Thus, in general, our simplified dispersion relation for low-frequency modes in a two-species plasma has the form of a quartic in ![]() $\omega$, rather than a quadratic, if
$\omega$, rather than a quadratic, if ![]() $k_{\|} \rho _s \ll 1$ for at least the electron species. Physically, the reason why a quadratic dispersion relation is no longer a reasonable approximation is the existence of more than two low-frequency modes in a two-species Maxwellian plasma in certain wavenumber regimes. For example, for quasi-parallel modes with characteristic parallel wavenumbers satisfying
$k_{\|} \rho _s \ll 1$ for at least the electron species. Physically, the reason why a quadratic dispersion relation is no longer a reasonable approximation is the existence of more than two low-frequency modes in a two-species Maxwellian plasma in certain wavenumber regimes. For example, for quasi-parallel modes with characteristic parallel wavenumbers satisfying ![]() $k_{\|} \rho _i \ll 1$, there are four low-frequency modes (see § 4.4.1). Nevertheless, in other situations, the components of
$k_{\|} \rho _i \ll 1$, there are four low-frequency modes (see § 4.4.1). Nevertheless, in other situations, the components of ![]() $\boldsymbol{\mathsf{M}}_s(\boldsymbol {k})$ for which the
$\boldsymbol{\mathsf{M}}_s(\boldsymbol {k})$ for which the ![]() $\boldsymbol{\mathsf{M}}_s(\tilde {\omega }_{s\|},\boldsymbol {k}) \approx \tilde {\omega }_{s\|} \boldsymbol{\mathsf{M}}_s^{(0)}(\boldsymbol {k})$ approximation breaks down are not important, on account of their small size compared with terms in the dispersion relation associated with other Maxwellian components. In this case, the original quadratic dispersion relation is sufficient. An explicit wavenumber regime in which this is realised is
$\boldsymbol{\mathsf{M}}_s(\tilde {\omega }_{s\|},\boldsymbol {k}) \approx \tilde {\omega }_{s\|} \boldsymbol{\mathsf{M}}_s^{(0)}(\boldsymbol {k})$ approximation breaks down are not important, on account of their small size compared with terms in the dispersion relation associated with other Maxwellian components. In this case, the original quadratic dispersion relation is sufficient. An explicit wavenumber regime in which this is realised is ![]() $k_{\|} \rho _e \sim k_{\perp } \rho _e \ll 1$ but
$k_{\|} \rho _e \sim k_{\perp } \rho _e \ll 1$ but ![]() $k \rho _i \gg 1$ – see §§ 4.3.4 and 4.4.7.
$k \rho _i \gg 1$ – see §§ 4.3.4 and 4.4.7.
Taking these multiple-species effects into account, the reasons behind the decision made in § 2.3.4 to consider the CES microinstabilities separately from the CET microinstabilities come into plain focus. First, the characteristic sizes of the CE electron-temperature-gradient and ion-temperature-gradient terms are comparable (![]() $\eta _i \sim \eta _e$), while the CE ion-shear term is much larger than the CE electron-shear term:
$\eta _i \sim \eta _e$), while the CE ion-shear term is much larger than the CE electron-shear term: ![]() $\epsilon _i \sim \mu _e^{-1/2} \epsilon _e$. This has the consequence that the natural orderings of
$\epsilon _i \sim \mu _e^{-1/2} \epsilon _e$. This has the consequence that the natural orderings of ![]() $\tilde {\omega }_{e\|}$ and
$\tilde {\omega }_{e\|}$ and ![]() $\tilde {\omega }_{i\|}$ with respect to other parameters are different for CES and CET microinstabilities. Secondly, the fact that the velocity-space anisotropy associated with the CE temperature-gradient terms differs from the CE shear terms – which excite microinstabilities with different characteristic wavevectors – means that the form of the dispersion relations of CET and CES microinstabilities are distinct. More specifically, the dispersion relation for CET microinstabilities at both electron and ion scales can always be simplified to a quadratic equation in
$\tilde {\omega }_{i\|}$ with respect to other parameters are different for CES and CET microinstabilities. Secondly, the fact that the velocity-space anisotropy associated with the CE temperature-gradient terms differs from the CE shear terms – which excite microinstabilities with different characteristic wavevectors – means that the form of the dispersion relations of CET and CES microinstabilities are distinct. More specifically, the dispersion relation for CET microinstabilities at both electron and ion scales can always be simplified to a quadratic equation in ![]() $\omega$; in contrast, for CES microinstabilities, the dispersion relation cannot in general be reduced to anything simpler than a quartic.
$\omega$; in contrast, for CES microinstabilities, the dispersion relation cannot in general be reduced to anything simpler than a quartic.
2.5.7. Modelling collisional effects on CE microinstabilities
As proposed thus far, our method for characterising microinstabilities in a CE plasma does not include explicitly the effect of collisions on the microinstabilities themselves. In principle, this can be worked out by introducing a collision operator into the linearised Maxwell–Vlasov–Landau equation from which the hot-plasma dispersion relation (2.75) is derived. Indeed, if a Krook collision operator is assumed (as was done in § 2.4.2 when determining the precise form of the CE distribution functions of ions and electrons), the resulting modification of the hot-plasma dispersion relation is quite simple: the conductivity tensor (2.77) remains the same, but with the substitution
in the resonant denominators (see Appendix C). As for how this affects the simplifications to the dispersion relation outlined in § 2.5.3, the expansion parameter in the dielectric tensor's expansion (2.99) is altered, becoming ![]() ${\hat {\omega }}_{s\|} \ll 1$ (as opposed to
${\hat {\omega }}_{s\|} \ll 1$ (as opposed to ![]() $\tilde {\omega }_{s\|} \ll 1$); in other words,
$\tilde {\omega }_{s\|} \ll 1$); in other words, ![]() $\|\boldsymbol {\mathfrak {E}}_s^{(1)}\|/\|\boldsymbol {\mathfrak {E}}_s^{(0)}\| \sim {\hat {\omega }}_{s\|}$.
$\|\boldsymbol {\mathfrak {E}}_s^{(1)}\|/\|\boldsymbol {\mathfrak {E}}_s^{(0)}\| \sim {\hat {\omega }}_{s\|}$.
The latter result leads to an seemingly counterintuitive conclusion: collisions typically fail to stabilise low-frequency instabilities in CE plasma if ![]() $\omega \tau _s \lesssim 1$ (where
$\omega \tau _s \lesssim 1$ (where ![]() $\tau _s$ is the collision time of species
$\tau _s$ is the collision time of species ![]() $s$) but
$s$) but ![]() $k_{\|} v_{\mathrm {th}i} \tau _s = k_{\|} \lambda _s \gg 1$. This is because the simplified dispersion relation (2.118) only involves leading-order terms in the expanded dielectric tensor. These terms are independent of
$k_{\|} v_{\mathrm {th}i} \tau _s = k_{\|} \lambda _s \gg 1$. This is because the simplified dispersion relation (2.118) only involves leading-order terms in the expanded dielectric tensor. These terms are independent of ![]() ${\hat {\omega }}_{s\|}$, and thus the growth rate of any microinstability that is adequately described by (2.118) does not depend on the size of
${\hat {\omega }}_{s\|}$, and thus the growth rate of any microinstability that is adequately described by (2.118) does not depend on the size of ![]() $\omega \tau _s$. For these microinstabilities, the effect of collisions only becomes relevant if
$\omega \tau _s$. For these microinstabilities, the effect of collisions only becomes relevant if
This is inconsistent with the assumptions ![]() $k \lambda _e \gg 1$,
$k \lambda _e \gg 1$, ![]() $k \lambda _i \gg 1$ made when setting up our calculation in § 2.4.1. Thus, the only regime where collisions can reasonably be included in our calculation is one where they are typically not important. An exception to this rule arises when two-species plasma effects mean that the first-order terms in the
$k \lambda _i \gg 1$ made when setting up our calculation in § 2.4.1. Thus, the only regime where collisions can reasonably be included in our calculation is one where they are typically not important. An exception to this rule arises when two-species plasma effects mean that the first-order terms in the ![]() ${\hat {\omega }}_{s\|} \ll 1$ expansion are needed for a correct characterisation of the growth rate of certain microinstabilities (see § 2.5.6); for these instabilities, we include the effect of collisions using (2.124).
${\hat {\omega }}_{s\|} \ll 1$ expansion are needed for a correct characterisation of the growth rate of certain microinstabilities (see § 2.5.6); for these instabilities, we include the effect of collisions using (2.124).
Although our calculation is not formally valid when (2.125) holds, so we cannot show explicitly that growth ceases, this condition nonetheless represents a sensible criterion for suppression of microinstabilities by collisional damping. Physically, it signifies that collisions are strong enough to scatter a particle before it has streamed across a typical wavelength of fluctuation excited by a microinstability. This collisional scattering prevents particles from being resonant, which in turn would suppress the growth of many different microinstabilities. However, we acknowledge that there exist microinstabilities that do not involve resonant-particle populations (e.g., the firehose instability – see §§ 2.3.3 and 4.4.1), and thus it cannot be rigorously concluded from our work that all microinstabilities are suppressed when (2.125) applies.
Yet even without an actual proof of collisional stabilisation, there is another reason implying that (2.125) is a reasonable threshold for microinstabilities: the characteristic growth time of microinstabilities at wavenumbers satisfying (2.125) is comparable to the evolution time ![]() $\tau _L$ of macroscopic motions in the plasma. To illustrate this idea, we consider the ordering (2.94) relating the complex frequency of microinstabilities to the small parameter
$\tau _L$ of macroscopic motions in the plasma. To illustrate this idea, we consider the ordering (2.94) relating the complex frequency of microinstabilities to the small parameter ![]() $\epsilon _s$ for CES (CE shear-driven) microinstabilities, and use it to estimate
$\epsilon _s$ for CES (CE shear-driven) microinstabilities, and use it to estimate
where ![]() $V \sim L_V/\tau _L$ is the characteristic ion bulk-flow velocity. Considering orderings (2.55), it follows that
$V \sim L_V/\tau _L$ is the characteristic ion bulk-flow velocity. Considering orderings (2.55), it follows that ![]() $\epsilon _e \sim \mu _e^{1/2} \epsilon _i$, and so
$\epsilon _e \sim \mu _e^{1/2} \epsilon _i$, and so
Then (2.126) becomes
implying (as claimed) that the CES microinstability growth rate is smaller than the fluid turnover rate ![]() $\tau _L^{-1}$. Spelled out clearly, this means that the underlying quasiequilibrium state changes before going unstable. Similar arguments can be applied to CET (CE temperature-gradient-driven) microinstabilities.
$\tau _L^{-1}$. Spelled out clearly, this means that the underlying quasiequilibrium state changes before going unstable. Similar arguments can be applied to CET (CE temperature-gradient-driven) microinstabilities.
Thus, (2.125) represents a lower bound on the characteristic wavenumbers at which microinstabilities can operate. We shall therefore assume throughout the rest of this paper that microinstabilities are suppressed (or rendered irrelevant) if they satisfy (2.125).
2.5.8. Caveats: microinstabilities in CE plasma where  $\omega /k_{\|} v_{\mathrm {th}s} \not \sim \eta _s, \epsilon _s$
$\omega /k_{\|} v_{\mathrm {th}s} \not \sim \eta _s, \epsilon _s$
As mentioned in § 2.4.2, there are a number of important caveats to the claim that the ordering (2.94) must be satisfied by microinstabilities in a CE plasma.
The first of these is that our comparison of non-Maxwellian with the Maxwellian terms in expression (2.93) for ![]() $\varXi _s$ is in essence a pointwise comparison at characteristic values of
$\varXi _s$ is in essence a pointwise comparison at characteristic values of ![]() $\tilde {v}_s$ for which
$\tilde {v}_s$ for which ![]() $\varXi _s$ attains its largest typical magnitude. However,
$\varXi _s$ attains its largest typical magnitude. However, ![]() $\varXi _s$ affects the components of the conductivity tensor via the velocity integral of its product with a complicated function of frequency and wavenumber (see (2.77)). Thus, it does not necessarily follow that the ratio of the integrated responses of the Maxwellian and non-Maxwellian contributions to the conductivity tensor is the same as the pointwise ratio of the respective contributions to
$\varXi _s$ affects the components of the conductivity tensor via the velocity integral of its product with a complicated function of frequency and wavenumber (see (2.77)). Thus, it does not necessarily follow that the ratio of the integrated responses of the Maxwellian and non-Maxwellian contributions to the conductivity tensor is the same as the pointwise ratio of the respective contributions to ![]() $\varXi _s$. In some circumstances, this can result in the Maxwellian part being smaller than anticipated, leading to faster microinstabilities. An example of this phenomenon was given in § 2.5.6: for
$\varXi _s$. In some circumstances, this can result in the Maxwellian part being smaller than anticipated, leading to faster microinstabilities. An example of this phenomenon was given in § 2.5.6: for ![]() $k_{\|} \rho _s \ll 1$, the characteristic magnitude of the Maxwellian contribution to some components of the dielectric tensor is
$k_{\|} \rho _s \ll 1$, the characteristic magnitude of the Maxwellian contribution to some components of the dielectric tensor is ![]() ${O}(\tilde {\omega }_{s\|}^2)$, as compared with the naive estimate
${O}(\tilde {\omega }_{s\|}^2)$, as compared with the naive estimate ![]() ${O}(\tilde {\omega }_{s\|})$. This leads to certain CES microinstabilities (for example, the CE ion-shear-driven firehose instability – § 4.4.1) satisfying a modified low-frequency condition
${O}(\tilde {\omega }_{s\|})$. This leads to certain CES microinstabilities (for example, the CE ion-shear-driven firehose instability – § 4.4.1) satisfying a modified low-frequency condition
A similar phenomenon affects the limit ![]() $k_{\|} \rightarrow 0$ for fixed
$k_{\|} \rightarrow 0$ for fixed ![]() $k_{\bot }$, in which case it can be shown that the Maxwellian contribution to
$k_{\bot }$, in which case it can be shown that the Maxwellian contribution to ![]() $\sigma _{zz}$ is
$\sigma _{zz}$ is ![]() ${O}(k_{\|}/k_{\bot })$; this leads to a CES microinstability (the CE electron-shear-driven ordinary-mode instability – see § 4.4.11) satisfying a modified ordering
${O}(k_{\|}/k_{\bot })$; this leads to a CES microinstability (the CE electron-shear-driven ordinary-mode instability – see § 4.4.11) satisfying a modified ordering
The second caveat is that for some plasma modes, the particles predominantly responsible for collisionless damping or growth are suprathermal, i.e. ![]() $\tilde {v}_s \gg 1$. Then the previous comparison of terms in (2.93) is not applicable. Modes of this sort are the quasi-cold plasma modes discussed in § 2.3.4 and Appendix D. They can be unstable, but always with a growth rate that is exponentially small in
$\tilde {v}_s \gg 1$. Then the previous comparison of terms in (2.93) is not applicable. Modes of this sort are the quasi-cold plasma modes discussed in § 2.3.4 and Appendix D. They can be unstable, but always with a growth rate that is exponentially small in ![]() $\eta _s$ and
$\eta _s$ and ![]() $\epsilon _s$.
$\epsilon _s$.
In spite of these two caveats, we proceed by considering the full hot-plasma dispersion relation (2.75) in the low-frequency limit ![]() $\omega \ll k_{\|} v_{\mathrm {th}s}$. This approach enables the treatment of all microinstabilities satisfying condition
$\omega \ll k_{\|} v_{\mathrm {th}s}$. This approach enables the treatment of all microinstabilities satisfying condition
where ![]() ${\iota _\eta }$ and
${\iota _\eta }$ and ![]() ${\iota _\epsilon }$ are fractional powers not much smaller than unity. Similarly to the discussion in § 2.3.4, we claim that the microinstabilities satisfying the low-frequency condition (2.131a,b) are likely to be the most rapid of all possible microinstabilities in CE plasma. A formal justification of this claim relies on the argument – presented in Appendix E – that for all plasma modes satisfying
${\iota _\epsilon }$ are fractional powers not much smaller than unity. Similarly to the discussion in § 2.3.4, we claim that the microinstabilities satisfying the low-frequency condition (2.131a,b) are likely to be the most rapid of all possible microinstabilities in CE plasma. A formal justification of this claim relies on the argument – presented in Appendix E – that for all plasma modes satisfying ![]() $\omega \gtrsim k_{\|} v_{\mathrm {th}s}$ and
$\omega \gtrsim k_{\|} v_{\mathrm {th}s}$ and ![]() $|{\rm Re}\,{\omega }| \gg |{\rm Im}\,{\omega }|$, the growth rate is exponentially small in
$|{\rm Re}\,{\omega }| \gg |{\rm Im}\,{\omega }|$, the growth rate is exponentially small in ![]() $\eta _s$ and
$\eta _s$ and ![]() $\epsilon _s$. By definition, this class of modes includes the quasi-cold modes. In a plasma where
$\epsilon _s$. By definition, this class of modes includes the quasi-cold modes. In a plasma where ![]() $\epsilon _s, \eta _s \ll 1$, the growth rates of such microinstabilities will be exponentially small, and thus of little significance. The only situation that we are aware of in which the low-frequency condition (2.131a,b) is not appropriate is the aforementioned CES ordinary-mode instability; a separate treatment of it involving the full hot-plasma dispersion relation is provided in Appendix K.3.13.
$\epsilon _s, \eta _s \ll 1$, the growth rates of such microinstabilities will be exponentially small, and thus of little significance. The only situation that we are aware of in which the low-frequency condition (2.131a,b) is not appropriate is the aforementioned CES ordinary-mode instability; a separate treatment of it involving the full hot-plasma dispersion relation is provided in Appendix K.3.13.
3. CET (Chapman–Enskog, temperature-gradient-driven) microinstabilities
3.1. Form of CE distribution function
We consider first the non-Maxwellian terms of the CE distribution function arising from temperature gradients and electron–ion drifts. Neglecting bulk-flow gradients (viz. setting ![]() $\epsilon _s = 0$ for both species – see (2.11e, f)), the CE distribution functions (2.72) for the electrons and ions become
$\epsilon _s = 0$ for both species – see (2.11e, f)), the CE distribution functions (2.72) for the electrons and ions become
where we have written out explicitly the electron-temperature-gradient (![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _i$ – see (2.11a,d)) and electron-friction (
$\eta _i$ – see (2.11a,d)) and electron-friction (![]() $\eta _e^R$ – see (2.11b)) terms under the assumption that the Maxwell–Vlasov–Landau system from which these CE distribution functions were derived is governed by a Krook collision operator. We remind the reader that the electron–ion-drift term (
$\eta _e^R$ – see (2.11b)) terms under the assumption that the Maxwell–Vlasov–Landau system from which these CE distribution functions were derived is governed by a Krook collision operator. We remind the reader that the electron–ion-drift term (![]() $\eta _e^u$ – see (2.11c)) disappears for this choice of collision operator. We also observe that the non-Maxwellian part of the distribution functions (3.1) have odd parity; thus, any unstable mode with
$\eta _e^u$ – see (2.11c)) disappears for this choice of collision operator. We also observe that the non-Maxwellian part of the distribution functions (3.1) have odd parity; thus, any unstable mode with ![]() $k_{\|} > 0$ has a corresponding unstable mode with
$k_{\|} > 0$ has a corresponding unstable mode with ![]() $k_{\|} < 0$ and the signs of
$k_{\|} < 0$ and the signs of ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$, and
$\eta _e^R$, and ![]() $\eta _i$ reversed (see § 2.5.5, last paragraph). For the rest of this section, we therefore take
$\eta _i$ reversed (see § 2.5.5, last paragraph). For the rest of this section, we therefore take ![]() $k_{\|} > 0$ without loss of generality; the behaviour of modes with
$k_{\|} > 0$ without loss of generality; the behaviour of modes with ![]() $k_{\|} < 0$ can be inferred via this symmetry relation.
$k_{\|} < 0$ can be inferred via this symmetry relation.
The precise methodology that we employ to calculate the growth rates of CET microinstabilities is described in Appendix J; here, we focus on the results of those calculations. In § 3.2, we will present the overview of the CET stability landscape, while the microinstabilities referred to there will be treated analytically in § 3.3.
3.2. Stability
We determine the stability (or otherwise) of the CE distribution functions of the form (3.1a) and (3.2b) for different values of ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$ and
$\eta _e^R$ and ![]() $\eta _i$, the electron inertial scale
$\eta _i$, the electron inertial scale ![]() $d_e$, the electron-temperature scale length
$d_e$, the electron-temperature scale length ![]() $L_T = |\boldsymbol {\nabla }_{\|} \log {T_e}|^{-1}$ and for fixed electron and ion plasma betas (
$L_T = |\boldsymbol {\nabla }_{\|} \log {T_e}|^{-1}$ and for fixed electron and ion plasma betas (![]() $\beta _e$ and
$\beta _e$ and ![]() $\beta _i$, respectively). Stability calculations are carried out for particular combinations of values of
$\beta _i$, respectively). Stability calculations are carried out for particular combinations of values of ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$,
$\eta _e^R$, ![]() $\eta _i$,
$\eta _i$, ![]() $d_e$,
$d_e$, ![]() $L_T$,
$L_T$, ![]() $\beta _e$ and
$\beta _e$ and ![]() $\beta _i$ by solving for the maximum microinstability growth rate across all wavevectors (see Appendix J for explanation of how this is done), and determining whether this growth rate is positive for the microinstabilities whose wavelength is smaller than the Coulomb mean free paths (a condition necessary for our calculation to be valid).
$\beta _i$ by solving for the maximum microinstability growth rate across all wavevectors (see Appendix J for explanation of how this is done), and determining whether this growth rate is positive for the microinstabilities whose wavelength is smaller than the Coulomb mean free paths (a condition necessary for our calculation to be valid).
The results of one such stability calculation – for a temperature-equilibrated hydrogen plasma (![]() $\eta _e^T = \eta _i$,
$\eta _e^T = \eta _i$, ![]() $\beta _i = \beta _e$) – are presented in figure 2. In spite of the five-dimensional (
$\beta _i = \beta _e$) – are presented in figure 2. In spite of the five-dimensional (![]() $\eta _e^T,\eta _e^R,d_e/L_T,\beta _e$) parameter space that seemingly needs to be explored, we can, in fact, convey the most salient information concerning the stability of the CE distribution functions (3.1) using plots over a two-dimensional
$\eta _e^T,\eta _e^R,d_e/L_T,\beta _e$) parameter space that seemingly needs to be explored, we can, in fact, convey the most salient information concerning the stability of the CE distribution functions (3.1) using plots over a two-dimensional ![]() $(d_e/L_T,\lambda _e/L_T)$ parameter space at a fixed
$(d_e/L_T,\lambda _e/L_T)$ parameter space at a fixed ![]() $\beta _e$ (where we remind the reader that
$\beta _e$ (where we remind the reader that ![]() $\lambda _e/L_T = |\eta _e^T|$ – see (2.11a)). This reduction in phase-space dimensionality is possible for two reasons. First, dimensional analysis implies that the salient stability thresholds of CET microinstabilities cannot depend on
$\lambda _e/L_T = |\eta _e^T|$ – see (2.11a)). This reduction in phase-space dimensionality is possible for two reasons. First, dimensional analysis implies that the salient stability thresholds of CET microinstabilities cannot depend on ![]() $d_e$ and
$d_e$ and ![]() $L_T$ separately, but only on the ratio
$L_T$ separately, but only on the ratio ![]() $d_e/L_T$. Secondly, it transpires that the CE electron-friction term of the form given in (3.1a) does not drive any microinstabilities, bur merely modifies the real frequency of perturbations with respect to their Maxwellian frequencies (this is proven in Appendix J.1). Thus, we can set
$d_e/L_T$. Secondly, it transpires that the CE electron-friction term of the form given in (3.1a) does not drive any microinstabilities, bur merely modifies the real frequency of perturbations with respect to their Maxwellian frequencies (this is proven in Appendix J.1). Thus, we can set ![]() $\eta _e^R = 0$ without qualitatively altering the stability properties of the CE distribution functions (3.1).
$\eta _e^R = 0$ without qualitatively altering the stability properties of the CE distribution functions (3.1).

Figure 2. The CE-distribution-function stability map for CET microinstabilities. Exploration of the stability of the CE distribution functions (3.1a) and (3.1b) for different values of small parameters ![]() $\eta _e^T$,
$\eta _e^T$, ![]() $\eta _e^R$ and
$\eta _e^R$ and ![]() $\eta _i$, and the ratio of the electron inertial scale
$\eta _i$, and the ratio of the electron inertial scale ![]() $d_e$ to the temperature scale length
$d_e$ to the temperature scale length ![]() $L_T$, in a temperature-equilibrated hydrogen plasma. In this plot, we chose
$L_T$, in a temperature-equilibrated hydrogen plasma. In this plot, we chose ![]() $\eta _e^R = 0$ and
$\eta _e^R = 0$ and ![]() $\eta _e^T = \eta _i$, and then show
$\eta _e^T = \eta _i$, and then show ![]() $\lambda _e/L_T = |\eta _e^T|$ with equal logarithmic spacing in the range
$\lambda _e/L_T = |\eta _e^T|$ with equal logarithmic spacing in the range ![]() $[10^{-5},10^{0}]$;
$[10^{-5},10^{0}]$; ![]() $d_e/L_T$ is chosen with equal logarithmic spacing in the range
$d_e/L_T$ is chosen with equal logarithmic spacing in the range ![]() $[10^{-15},10^{0}]$. The total size of the grid is
$[10^{-15},10^{0}]$. The total size of the grid is ![]() $400^2$. For reasons of efficiency, we calculate growth rates on a
$400^2$. For reasons of efficiency, we calculate growth rates on a ![]() $40^2$ grid in wavenumber space with logarithmic spacing for both parallel and perpendicular wavenumbers. In this plot,
$40^2$ grid in wavenumber space with logarithmic spacing for both parallel and perpendicular wavenumbers. In this plot, ![]() $\beta _e = \beta _i = 10^4$. (a) Stable (blue) and unstable (red) regions of
$\beta _e = \beta _i = 10^4$. (a) Stable (blue) and unstable (red) regions of ![]() $(d_e/L_T,\lambda _e/L_T)$ phase space. The theoretically anticipated collisional cutoff (right – see (3.4)) and
$(d_e/L_T,\lambda _e/L_T)$ phase space. The theoretically anticipated collisional cutoff (right – see (3.4)) and ![]() $\beta$-stabilisation threshold (bottom) of the CET whistler instability are shown as black dashed lines. (b) Maximum normalised microinstability growth rate (red) vs
$\beta$-stabilisation threshold (bottom) of the CET whistler instability are shown as black dashed lines. (b) Maximum normalised microinstability growth rate (red) vs ![]() $\lambda _e/L_T$ for a fixed electron inertial scale
$\lambda _e/L_T$ for a fixed electron inertial scale ![]() $d_e/L_T = 10^{-15}$, along with analytically predicted maximum growth rate for the CET whistler instability in the limit
$d_e/L_T = 10^{-15}$, along with analytically predicted maximum growth rate for the CET whistler instability in the limit ![]() $\lambda _e \beta _e/L_T \gg 1$ (blue, see (3.10)). (c) Parallel wavenumber of fastest-growing microinstability (red) vs
$\lambda _e \beta _e/L_T \gg 1$ (blue, see (3.10)). (c) Parallel wavenumber of fastest-growing microinstability (red) vs ![]() $\lambda _e/L_T$ for a fixed electron inertial scale
$\lambda _e/L_T$ for a fixed electron inertial scale ![]() $d_e/L_T = 10^{-15}$, along with the same quantity analytically predicted for the CET whistler instability in the limit
$d_e/L_T = 10^{-15}$, along with the same quantity analytically predicted for the CET whistler instability in the limit ![]() $\lambda _e \beta _e/L_T \gg 1$ (blue, see (3.11)). (d) Wavevector angle
$\lambda _e \beta _e/L_T \gg 1$ (blue, see (3.11)). (d) Wavevector angle ![]() $\theta \equiv \tan ^{-1}{(k_{\perp }/k_{\|})}$ of the fastest-growing instability over
$\theta \equiv \tan ^{-1}{(k_{\perp }/k_{\|})}$ of the fastest-growing instability over ![]() $(d_e/L_T,\lambda _e/L_T)$ parameter space.
$(d_e/L_T,\lambda _e/L_T)$ parameter space.
Figure 2(a) shows the regions of instability and stability of the CE distribution function (3.1) over the ![]() $(d_e/L_T,\lambda _e/L_T)$ parameter space. The unstable region is bracketed by two thresholds. For
$(d_e/L_T,\lambda _e/L_T)$ parameter space. The unstable region is bracketed by two thresholds. For ![]() $d_e/L_T$ below a critical value
$d_e/L_T$ below a critical value ![]() $(d_e/L_T)_{c0}$, stability is independent of
$(d_e/L_T)_{c0}$, stability is independent of ![]() $d_e/L_T$, and only depends on the relative magnitude of
$d_e/L_T$, and only depends on the relative magnitude of ![]() $\lambda _e/L_T$ and
$\lambda _e/L_T$ and ![]() $\beta _e$: CET microinstabilities are quenched if
$\beta _e$: CET microinstabilities are quenched if ![]() $\lambda _e \beta _e/L_T \ll 1$. For
$\lambda _e \beta _e/L_T \ll 1$. For ![]() $d_e/L_T \gtrsim (d_e/L_T)_{c0}$, and
$d_e/L_T \gtrsim (d_e/L_T)_{c0}$, and ![]() $\lambda _e \beta _e/L_T \gtrsim 1$, stability is attained at fixed
$\lambda _e \beta _e/L_T \gtrsim 1$, stability is attained at fixed ![]() $\lambda _e/L_T$ for
$\lambda _e/L_T$ for ![]() $d_e/L_T > (d_e/L_T)_{c}$, where
$d_e/L_T > (d_e/L_T)_{c}$, where ![]() $(d_e/L_T)_{c}$ increases monotonically with
$(d_e/L_T)_{c}$ increases monotonically with ![]() $\lambda _e/L_T$. If
$\lambda _e/L_T$. If ![]() $\lambda _e \beta _e/L_T \gtrsim 1$ and
$\lambda _e \beta _e/L_T \gtrsim 1$ and ![]() $d_e/L_T \lesssim (d_e/L_T)_{c}$, then the CE distribution function (3.1) is unstable.
$d_e/L_T \lesssim (d_e/L_T)_{c}$, then the CE distribution function (3.1) is unstable.
The fastest-growing CET microinstability is the whistler (heat-flux) instability: whistler waves driven unstable by the small anisotropy of the CE electron-temperature-gradient term (see § 3.3.1). That this instability with wavevector parallel to the magnetic field is indeed the dominant microinstability is most easily ascertained by comparing simple analytic expressions for its peak growth rate and wavevector with the equivalent quantities recorded when performing the general stability calculation (see figure 2b–d). The maximum microinstability growth rate matches the analytic result (3.10) for the CET whistler instability in the limit ![]() $\lambda _e \beta _e/L_T \gg 1$, while the parallel wavenumber
$\lambda _e \beta _e/L_T \gg 1$, while the parallel wavenumber ![]() $(|k_{\|}| \rho _e)_{\rm peak}$ of the fastest-growing mode is extremely well described by (3.11). In addition, figure 2(d) demonstrates that the parallel instability is indeed the fastest. The CET whistler instability has been considered previously by a number of authors (see references in § 3.3.1); we note that these prior studies of this instability suggest that, nonlinearly, oblique CET whistler modes may be the more important ones, even though linearly the parallel modes are the fastest growing (see § 3.3.2).
$(|k_{\|}| \rho _e)_{\rm peak}$ of the fastest-growing mode is extremely well described by (3.11). In addition, figure 2(d) demonstrates that the parallel instability is indeed the fastest. The CET whistler instability has been considered previously by a number of authors (see references in § 3.3.1); we note that these prior studies of this instability suggest that, nonlinearly, oblique CET whistler modes may be the more important ones, even though linearly the parallel modes are the fastest growing (see § 3.3.2).
The two thresholds demarcating the unstable region can then be associated with stabilisation conditions of the CET whistler instability, each with a simple physical interpretation. The first condition is the ![]() $\beta$-stabilisation condition of the whistler instability. It is shown in § 3.3.1 that when
$\beta$-stabilisation condition of the whistler instability. It is shown in § 3.3.1 that when ![]() $\lambda _e \beta _e/L_T \ll 1$, cyclotron damping on whistler modes is sufficiently strong that only quasi-parallel modes with parallel wavenumbers
$\lambda _e \beta _e/L_T \ll 1$, cyclotron damping on whistler modes is sufficiently strong that only quasi-parallel modes with parallel wavenumbers ![]() $k_{\|} \rho _e \lesssim (\lambda _e \beta _e/L_T)^{1/3} \ll 1$ can be destabilised by the anisotropy of the CE distribution function, and that the peak growth rate
$k_{\|} \rho _e \lesssim (\lambda _e \beta _e/L_T)^{1/3} \ll 1$ can be destabilised by the anisotropy of the CE distribution function, and that the peak growth rate ![]() $\gamma _{{\rm whistler},T}$ of these unstable modes is exponentially small in
$\gamma _{{\rm whistler},T}$ of these unstable modes is exponentially small in ![]() $\lambda _e \beta _e/L_T$ compared with the electron Larmor frequency (see (3.8)):
$\lambda _e \beta _e/L_T$ compared with the electron Larmor frequency (see (3.8)): ![]() $\gamma _{{\rm whistler},T}/\varOmega _e \sim \lambda _e \exp {[-(\lambda _e \beta _e/2 L_T)^{-2/3}]}/L_T$. This means that if
$\gamma _{{\rm whistler},T}/\varOmega _e \sim \lambda _e \exp {[-(\lambda _e \beta _e/2 L_T)^{-2/3}]}/L_T$. This means that if ![]() $\lambda _e \beta _e/L_T$ is reduced below unity, the growth rate of the CET whistler instability decreases dramatically, and thus the instability is unable to operate effectively on time scales shorter than those over which the CE plasma is evolving macroscopically.
$\lambda _e \beta _e/L_T$ is reduced below unity, the growth rate of the CET whistler instability decreases dramatically, and thus the instability is unable to operate effectively on time scales shorter than those over which the CE plasma is evolving macroscopically.
The second condition is collisional stabilisation of the CET whistler instability. Naively, it might be expected that two conditions must be satisfied in order for the microinstability to operate: that its growth rate must satisfy ![]() $\gamma _{{\rm whistler},T} \tau _{e} \gg 1$, and its characteristic wavenumber
$\gamma _{{\rm whistler},T} \tau _{e} \gg 1$, and its characteristic wavenumber ![]() $k \lambda _{e} \gg 1$ (see (2.125)). Noting that for the CET whistler instability (cf. (3.10)),
$k \lambda _{e} \gg 1$ (see (2.125)). Noting that for the CET whistler instability (cf. (3.10)),
 \begin{equation} \frac{\gamma_{{\rm whistler},T} \tau_{e}}{k \lambda_{e}} = \frac{\gamma_{{\rm whistler},T}}{k v_{\mathrm{th}e}} \sim \frac{\lambda_e}{L_T} \left( \frac{\lambda_e \beta_e}{L_T} \right)^{{-}1/5} \ll 1 , \end{equation}
\begin{equation} \frac{\gamma_{{\rm whistler},T} \tau_{e}}{k \lambda_{e}} = \frac{\gamma_{{\rm whistler},T}}{k v_{\mathrm{th}e}} \sim \frac{\lambda_e}{L_T} \left( \frac{\lambda_e \beta_e}{L_T} \right)^{{-}1/5} \ll 1 , \end{equation}
it follows that the former condition is more restrictive. Written as a condition on ![]() $d_e/L_T$ in terms of
$d_e/L_T$ in terms of ![]() $\lambda _e/L_T$ (and using
$\lambda _e/L_T$ (and using ![]() $\gamma _{{\rm whistler},T} \sim \lambda _e \varOmega _e/L_T$ – see (3.10)),
$\gamma _{{\rm whistler},T} \sim \lambda _e \varOmega _e/L_T$ – see (3.10)), ![]() $\gamma _{{\rm whistler},T} \tau _{e} \gg 1$ becomes
$\gamma _{{\rm whistler},T} \tau _{e} \gg 1$ becomes
while the condition ![]() $k \lambda _{e} \gg 1$ on the instability wavenumber
$k \lambda _{e} \gg 1$ on the instability wavenumber ![]() $k_{\|} \rho _e \sim (\lambda _e \beta _e/L_T)^{1/5}$ (see (3.11)) leads to
$k_{\|} \rho _e \sim (\lambda _e \beta _e/L_T)^{1/5}$ (see (3.11)) leads to
 \begin{equation} \frac{d_e}{L_T} \ll \left(\frac{d_e}{L_T}\right)_{c} \equiv \beta_e^{{-}3/2} \left(\frac{\lambda_e \beta_e}{L_T}\right)^{6/5} . \end{equation}
\begin{equation} \frac{d_e}{L_T} \ll \left(\frac{d_e}{L_T}\right)_{c} \equiv \beta_e^{{-}3/2} \left(\frac{\lambda_e \beta_e}{L_T}\right)^{6/5} . \end{equation}
It is the latter that agrees well with the true result, as shown in figure 2(a), implying that ![]() $(d_e/L_T)_{c0} = \beta _e^{-3/2}$. The (arguably surprising) result that the CET whistler instability can operate even if
$(d_e/L_T)_{c0} = \beta _e^{-3/2}$. The (arguably surprising) result that the CET whistler instability can operate even if ![]() $\gamma _{{\rm whistler},T} \tau _{e} \lesssim 1$ is, in fact, a generic feature of low-frequency (viz.
$\gamma _{{\rm whistler},T} \tau _{e} \lesssim 1$ is, in fact, a generic feature of low-frequency (viz. ![]() $\omega \ll k v_{\mathrm {th}e}$) plasma instabilities (see § 2.5.7). The physical instability mechanism underlying such modes can be sustained provided the time taken for thermal particles (in this case, electrons) to cross the mode's wavelength is much shorter than the collision time, irrespective of the mode's own frequency – in other words,
$\omega \ll k v_{\mathrm {th}e}$) plasma instabilities (see § 2.5.7). The physical instability mechanism underlying such modes can be sustained provided the time taken for thermal particles (in this case, electrons) to cross the mode's wavelength is much shorter than the collision time, irrespective of the mode's own frequency – in other words, ![]() $\tau _e k v_{\mathrm {th}e} = k \lambda _e \gg 1$. We point out that the collisional-stabilisation condition of the CET whistler instability can never be satisfied in a strongly magnetised plasma if
$\tau _e k v_{\mathrm {th}e} = k \lambda _e \gg 1$. We point out that the collisional-stabilisation condition of the CET whistler instability can never be satisfied in a strongly magnetised plasma if ![]() $\lambda _e \beta _e/L_T \gtrsim 1$: this is because its wavenumber
$\lambda _e \beta _e/L_T \gtrsim 1$: this is because its wavenumber ![]() $k$ satisfies
$k$ satisfies ![]() $k^{-1} \lesssim \rho _e \ll \lambda _e$.
$k^{-1} \lesssim \rho _e \ll \lambda _e$.
Whilst it is the fastest-growing one (assuming ![]() $\eta _e^T \sim \eta _i$), the CET whistler instability is not the only CET microinstability of interest. There are two other instabilities driven by the CET ion-temperature-gradient term, neither of which has previously been identified, to our knowledge: the slow (hydromagnetic) wave instability (see § 3.3.3), and the long-wavelength KAW instability (see § 3.3.4). The former, whose characteristic wavenumber scale satisfies
$\eta _e^T \sim \eta _i$), the CET whistler instability is not the only CET microinstability of interest. There are two other instabilities driven by the CET ion-temperature-gradient term, neither of which has previously been identified, to our knowledge: the slow (hydromagnetic) wave instability (see § 3.3.3), and the long-wavelength KAW instability (see § 3.3.4). The former, whose characteristic wavenumber scale satisfies ![]() $k \rho _i \sim 1$, has a larger characteristic growth rate
$k \rho _i \sim 1$, has a larger characteristic growth rate ![]() $\gamma _{\rm SW} \sim \lambda _i \varOmega _i/L_{T_i}$ (where
$\gamma _{\rm SW} \sim \lambda _i \varOmega _i/L_{T_i}$ (where ![]() $L_{T_i} = |\boldsymbol {\nabla }_{\|} \log {T_i}|^{-1}$ is the scale length of the ion-temperature gradient). Similarly to the CET whistler instability, the CET slow-wave instability has
$L_{T_i} = |\boldsymbol {\nabla }_{\|} \log {T_i}|^{-1}$ is the scale length of the ion-temperature gradient). Similarly to the CET whistler instability, the CET slow-wave instability has ![]() $\beta$-stabilisation and collisional-stabilisation conditions
$\beta$-stabilisation and collisional-stabilisation conditions ![]() $\lambda _i \beta _i/L_{T_i} \ll 1$ and
$\lambda _i \beta _i/L_{T_i} \ll 1$ and ![]() $\lambda _i \lesssim \rho _i$, respectively. Thus, unless
$\lambda _i \lesssim \rho _i$, respectively. Thus, unless ![]() $\lambda _i \beta _i/L_{T_i} > \lambda _e \beta _e/L_{T_e}$ (a condition equivalent to
$\lambda _i \beta _i/L_{T_i} > \lambda _e \beta _e/L_{T_e}$ (a condition equivalent to ![]() $\tau ^3 L_{T_e}/L_{T_i} > Z_i^3$, where
$\tau ^3 L_{T_e}/L_{T_i} > Z_i^3$, where ![]() $\tau = T_i/T_e$), the CET slow-wave instability only operates when the CET whistler-wave instability does, but on larger, ion rather than electron, scales. Nevertheless, the CET slow-wave instability is worth noting because, on account of being an ion instability, it should continue to operate even if the electron-scale CET whistler instability modifies the underlying electron distribution function. The slow-wave instability will then be responsible for modifying the ion distribution function. We are not aware of any work on the CET slow-wave instability and, thus, on its effect on ion heat conduction.
$\tau = T_i/T_e$), the CET slow-wave instability only operates when the CET whistler-wave instability does, but on larger, ion rather than electron, scales. Nevertheless, the CET slow-wave instability is worth noting because, on account of being an ion instability, it should continue to operate even if the electron-scale CET whistler instability modifies the underlying electron distribution function. The slow-wave instability will then be responsible for modifying the ion distribution function. We are not aware of any work on the CET slow-wave instability and, thus, on its effect on ion heat conduction.
Readers who are interested in knowing more about the properties and growth rates of CET microinstabilities are encouraged to continue § 3.3; those who are focused on the wider question of the kinetic stability of the CE distribution function should jump ahead to § 4.
3.3. CET microinstability classification
3.3.1. Parallel whistler (heat-flux) instability
The CET whistler instability, which has been studied previously by a number of authors (Levinson & Eichler Reference Levinson and Eichler1992; Pistinner & Eichler Reference Pistinner and Eichler1998; Gary & Li Reference Gary and Li2000; Roberg-Clark et al. Reference Roberg-Clark, Drake, Reynolds and Swisdak2016; Komarov et al. Reference Komarov, Schekochihin, Churazov and Spitkovsky2018; Roberg-Clark et al. Reference Roberg-Clark, Drake, Reynolds and Swisdak2018a,Reference Roberg-Clark, Drake, Swisdak and Reynoldsb; Kuzichev et al. Reference Kuzichev, Vasko, Soto-Chavez, Tong, Artemyev, Bale and Spitkovsky2019; Shaaban et al. Reference Shaaban, Lazar, Yoon, Poedts and López2019; Drake et al. Reference Drake, Pfrommer, Reynolds, Ruszkowski, Swisdak, Einarsson, Thomas, Hassam and Roberg-Clark2021), is driven by parallel electron heat fluxes. These heat fluxes introduce the asymmetry to the CE electron distribution function (i.e. the electron-temperature-gradient term), which, if it is sufficiently large, can overcome electron-cyclotron damping of (electromagnetic) whistler waves and render them unstable. The instability is mediated by gyroresonant wave–particle interactions that allow whistlers to drain free energy from electrons with parallel velocities ![]() $v_{\|} = \pm \varOmega _e/k_{\|}$. For a positive, parallel electron heat flux, which is driven by an anti-parallel temperature gradient (
$v_{\|} = \pm \varOmega _e/k_{\|}$. For a positive, parallel electron heat flux, which is driven by an anti-parallel temperature gradient (![]() $\boldsymbol {\nabla }_{\|} T_e < 0$, so
$\boldsymbol {\nabla }_{\|} T_e < 0$, so ![]() $\eta _e^T < 0$), it is only whistlers with a positive parallel wavenumber that are unstable. Whistler waves with both parallel and oblique wavevectors with respect to the magnetic field can be destabilised, although the parallel modes are the fastest-growing ones.
$\eta _e^T < 0$), it is only whistlers with a positive parallel wavenumber that are unstable. Whistler waves with both parallel and oblique wavevectors with respect to the magnetic field can be destabilised, although the parallel modes are the fastest-growing ones.
The CET whistler instability is most simply characterised analytically for parallel wavenumbers (i.e. ![]() $k = k_{\|}$). Then, it can be shown (see Appendix J.3.1, and also Levinson & Eichler Reference Levinson and Eichler1992; Roberg-Clark et al. Reference Roberg-Clark, Drake, Reynolds and Swisdak2016) that the real frequency
$k = k_{\|}$). Then, it can be shown (see Appendix J.3.1, and also Levinson & Eichler Reference Levinson and Eichler1992; Roberg-Clark et al. Reference Roberg-Clark, Drake, Reynolds and Swisdak2016) that the real frequency ![]() $\varpi$ and growth rate
$\varpi$ and growth rate ![]() $\gamma$ at arbitrary
$\gamma$ at arbitrary ![]() $k_{\|} > 0$ are given by
$k_{\|} > 0$ are given by
 $$\begin{align} \frac{\varpi}{\varOmega_e} &= \eta_e^T \left(\frac{k_\| \rho_e}{4} - \frac{1}{2 k_\| \rho_e}\right) - \frac{\left(\eta_e^T/2 + k_\|^3 \rho_e^3/\beta_e\right) {\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)} }{ \left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 + {\rm \pi}\exp{\left(-{2}/{k_\|^2 \rho_e^2}\right)}} , \end{align}$$
$$\begin{align} \frac{\varpi}{\varOmega_e} &= \eta_e^T \left(\frac{k_\| \rho_e}{4} - \frac{1}{2 k_\| \rho_e}\right) - \frac{\left(\eta_e^T/2 + k_\|^3 \rho_e^3/\beta_e\right) {\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)} }{ \left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 + {\rm \pi}\exp{\left(-{2}/{k_\|^2 \rho_e^2}\right)}} , \end{align}$$ $$\begin{align}\frac{\gamma}{\varOmega_e} &={-}\frac{\sqrt{\rm \pi}\left(\eta_e^T/2 + k_\|^3 \rho_e^3/\beta_e\right) }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 \exp{\left({1}/{k_\|^2 \rho_e^2}\right)}+ {\rm \pi}\exp{\left(-{1}/{k_\|^2 \rho_e^2}\right)}} . \end{align}$$
$$\begin{align}\frac{\gamma}{\varOmega_e} &={-}\frac{\sqrt{\rm \pi}\left(\eta_e^T/2 + k_\|^3 \rho_e^3/\beta_e\right) }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 \exp{\left({1}/{k_\|^2 \rho_e^2}\right)}+ {\rm \pi}\exp{\left(-{1}/{k_\|^2 \rho_e^2}\right)}} . \end{align}$$
For ![]() $\eta _e^T > 0$,
$\eta _e^T > 0$, ![]() $\gamma < 0$, but if
$\gamma < 0$, but if ![]() $\eta _e^T < 0$, then
$\eta _e^T < 0$, then ![]() $\gamma$ is non-negative for
$\gamma$ is non-negative for ![]() $k_{\|} \rho _e \leqslant (\eta _e^T \beta _e/2)^{1/3}$. The dispersion curves
$k_{\|} \rho _e \leqslant (\eta _e^T \beta _e/2)^{1/3}$. The dispersion curves ![]() $\varpi = \varpi (k_{\|})$ and
$\varpi = \varpi (k_{\|})$ and ![]() $\gamma = \gamma (k_\|)$ of unstable whistler waves with parallel wavevectors for three different values of
$\gamma = \gamma (k_\|)$ of unstable whistler waves with parallel wavevectors for three different values of ![]() $|\eta _e^T| \beta _e$ are plotted in figure 3 using the above formulae. For
$|\eta _e^T| \beta _e$ are plotted in figure 3 using the above formulae. For ![]() $|\eta _e^T| \beta _e \gtrsim 1$, the range of unstable parallel wavenumbers,
$|\eta _e^T| \beta _e \gtrsim 1$, the range of unstable parallel wavenumbers, ![]() $\Delta k_{\|}$, is comparable to the characteristic wavenumber of the instability:
$\Delta k_{\|}$, is comparable to the characteristic wavenumber of the instability: ![]() $\Delta k_{\|} \sim k_{\|} \sim \rho _e^{-1}$.
$\Delta k_{\|} \sim k_{\|} \sim \rho _e^{-1}$.

Figure 3. Parallel CET whistler instability. Dispersion curves of unstable whistler modes, whose instability is driven by the electron-temperature-gradient term in the CE distribution function (3.1a), for wavevectors that are co-parallel with the background magnetic field (viz. ![]() $\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The frequency (solid blue) and growth rates (solid red) of the modes are calculated using (3.5a) and (3.5b), respectively. The resulting frequencies and growth rates, when normalised as
$\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The frequency (solid blue) and growth rates (solid red) of the modes are calculated using (3.5a) and (3.5b), respectively. The resulting frequencies and growth rates, when normalised as ![]() $\gamma \beta _e/\varOmega _e$, are functions of the dimensionless quantity
$\gamma \beta _e/\varOmega _e$, are functions of the dimensionless quantity ![]() $\eta _e^{T} \beta _e$; we show the dispersion curves for three different values of
$\eta _e^{T} \beta _e$; we show the dispersion curves for three different values of ![]() $\eta _e^{T} \beta _e$. The approximations (3.6a) and (3.6b) for the frequency (dotted blue) and growth rate (dotted red) in the limit
$\eta _e^{T} \beta _e$. The approximations (3.6a) and (3.6b) for the frequency (dotted blue) and growth rate (dotted red) in the limit ![]() $k_{\|} \rho _e \ll 1$ are also plotted, as are the approximations (3.9a) and (3.9b) for the frequency (dashed blue) and growth rate (dashed red) in the limit
$k_{\|} \rho _e \ll 1$ are also plotted, as are the approximations (3.9a) and (3.9b) for the frequency (dashed blue) and growth rate (dashed red) in the limit ![]() $k_{\|} \rho _e \gg 1$.
$k_{\|} \rho _e \gg 1$.
The expressions (3.5a) and (3.5b) can be simplified in two subsidiary limits, which in turn allows for the derivation of analytic expressions for the maximum growth rate of the instability and the (parallel) wavenumber at which that growth rate is realised.
First, adopting the ordering ![]() $k_{\|} \rho _e \sim (|\eta _e^T| \beta _e)^{1/3} \ll 1$ under which the destabilising
$k_{\|} \rho _e \sim (|\eta _e^T| \beta _e)^{1/3} \ll 1$ under which the destabilising ![]() $\eta _e^T$ terms and the stabilising electron finite-Larmor-radius (FLR) terms are the same order, we find
$\eta _e^T$ terms and the stabilising electron finite-Larmor-radius (FLR) terms are the same order, we find
 $$\begin{align}\gamma &\approx{-}\frac{\sqrt{\rm \pi}}{k_\|^2 \rho_e^2} \left( \frac{\eta_e^T}{2} + \frac{k_\|^3 \rho_e^3}{\beta_e}\right) \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} \varOmega_e . \end{align}$$
$$\begin{align}\gamma &\approx{-}\frac{\sqrt{\rm \pi}}{k_\|^2 \rho_e^2} \left( \frac{\eta_e^T}{2} + \frac{k_\|^3 \rho_e^3}{\beta_e}\right) \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} \varOmega_e . \end{align}$$
The frequency corresponds to that of a whistler wave in the ![]() $k_{\|} \rho _e \ll 1$ limit (Boldyrev et al. Reference Boldyrev, Horaites, Xia and Perez2013). The fastest growth, which occurs at the wavenumber
$k_{\|} \rho _e \ll 1$ limit (Boldyrev et al. Reference Boldyrev, Horaites, Xia and Perez2013). The fastest growth, which occurs at the wavenumber
 \begin{equation} k_{\|} \rho_e \approx \left(\frac{|\eta_e^T| \beta_e}{2}\right)^{1/3} -\frac{|\eta_e^T| \beta_e}{4} , \end{equation}
\begin{equation} k_{\|} \rho_e \approx \left(\frac{|\eta_e^T| \beta_e}{2}\right)^{1/3} -\frac{|\eta_e^T| \beta_e}{4} , \end{equation}
is exponentially slow in ![]() $|\eta _e^T| \beta _e \ll 1$:
$|\eta _e^T| \beta _e \ll 1$:
 \begin{equation} \gamma_{\rm max} \approx \frac{3 \sqrt{\rm \pi}}{4} |\eta_e^T| \exp{\left[-\frac{2^{2/3}}{\left(|\eta_e^T| \beta_e\right)^{2/3}}-1\right]} \varOmega_e . \end{equation}
\begin{equation} \gamma_{\rm max} \approx \frac{3 \sqrt{\rm \pi}}{4} |\eta_e^T| \exp{\left[-\frac{2^{2/3}}{\left(|\eta_e^T| \beta_e\right)^{2/3}}-1\right]} \varOmega_e . \end{equation} Next, considering the opposite limit ![]() $k_\| \rho _e \gg 1$, we obtain
$k_\| \rho _e \gg 1$, we obtain
 $$\begin{align}\gamma &\approx{-}\frac{1}{\sqrt{\rm \pi}} \left[\eta_e^T \beta_e\left(\frac{1}{2}-\frac{4-{\rm \pi}}{2 {\rm \pi}k_{\|}^2 \rho_e^2}\right) + k_{\|}^3 \rho_e^3 \right] \frac{\varOmega_e}{\beta_e} . \end{align}$$
$$\begin{align}\gamma &\approx{-}\frac{1}{\sqrt{\rm \pi}} \left[\eta_e^T \beta_e\left(\frac{1}{2}-\frac{4-{\rm \pi}}{2 {\rm \pi}k_{\|}^2 \rho_e^2}\right) + k_{\|}^3 \rho_e^3 \right] \frac{\varOmega_e}{\beta_e} . \end{align}$$We then find that the maximum growth rate of the parallel mode is given by
 \begin{align} \gamma_{\rm max} & \approx \frac{|\eta_e^{T}|}{\sqrt{\rm \pi}} \left\{1- \left[\frac{1}{\sqrt{\rm \pi}}\left(\frac{4}{\rm \pi}-1\right)\right]^{3/5} \left[\left(\frac{3}{2}\right)^{2/5}-\left(\frac{2}{3}\right)^{3/5}\right]\left(|\eta_e^{T}|\beta_e \right)^{{-}2/5} \right\}\varOmega_e \nonumber\\ & \approx 0.56 |\eta_e^{T}| \left[1-0.13 \left(|\eta_e^{T}|\beta_e \right)^{{-}2/5} \right] \varOmega_e , \end{align}
\begin{align} \gamma_{\rm max} & \approx \frac{|\eta_e^{T}|}{\sqrt{\rm \pi}} \left\{1- \left[\frac{1}{\sqrt{\rm \pi}}\left(\frac{4}{\rm \pi}-1\right)\right]^{3/5} \left[\left(\frac{3}{2}\right)^{2/5}-\left(\frac{2}{3}\right)^{3/5}\right]\left(|\eta_e^{T}|\beta_e \right)^{{-}2/5} \right\}\varOmega_e \nonumber\\ & \approx 0.56 |\eta_e^{T}| \left[1-0.13 \left(|\eta_e^{T}|\beta_e \right)^{{-}2/5} \right] \varOmega_e , \end{align}at the parallel wavenumber
 \begin{equation} k_{\|} \rho_e = \left[\frac{2}{3\sqrt{\rm \pi}}\left(\frac{4}{\rm \pi}-1\right)\right]^{1/5} \left(|\eta_e^{T}|\beta_e \right)^{1/5} \approx 0. 63 \left(|\eta_e^{T}|\beta_e \right)^{1/5} . \end{equation}
\begin{equation} k_{\|} \rho_e = \left[\frac{2}{3\sqrt{\rm \pi}}\left(\frac{4}{\rm \pi}-1\right)\right]^{1/5} \left(|\eta_e^{T}|\beta_e \right)^{1/5} \approx 0. 63 \left(|\eta_e^{T}|\beta_e \right)^{1/5} . \end{equation}
In addition, we see that the real frequency of modes with ![]() $k_\| \rho _e \lesssim (|\eta _e^T| \beta _e/{2})^{1/3}$ is larger than the growth rate of the mode:
$k_\| \rho _e \lesssim (|\eta _e^T| \beta _e/{2})^{1/3}$ is larger than the growth rate of the mode: ![]() $\varpi \sim k_\| \rho _e \gamma \gg \gamma$. Thus, these modes oscillate more rapidly than they grow.
$\varpi \sim k_\| \rho _e \gamma \gg \gamma$. Thus, these modes oscillate more rapidly than they grow.
The approximate expressions for (3.6) and (3.9) are valid in the limits ![]() $|\eta _e^T| \beta _e \ll 1$ and
$|\eta _e^T| \beta _e \ll 1$ and ![]() $|\eta _e^T| \beta _e \gg 1$, respectively, and are plotted in figure 3 alongside the exact results (3.5). Of particular note is the accuracy of the approximate expression (3.9b) for the growth rate when
$|\eta _e^T| \beta _e \gg 1$, respectively, and are plotted in figure 3 alongside the exact results (3.5). Of particular note is the accuracy of the approximate expression (3.9b) for the growth rate when ![]() $k_{\|} \rho _e \gtrsim 0.6$; this suggests that (3.10) is a reasonable estimate of the peak growth rate for
$k_{\|} \rho _e \gtrsim 0.6$; this suggests that (3.10) is a reasonable estimate of the peak growth rate for ![]() $|\eta _e^T| \beta _e \gtrsim 1$.
$|\eta _e^T| \beta _e \gtrsim 1$.
3.3.2. Oblique whistler (heat-flux) instability
Analytical expressions for the frequency and growth rate of unstable modes with an oblique wavevector at an angle to the magnetic field are more complicated than the analogous expressions for parallel modes. In Appendix J.3, we show that there are two low-frequency oblique modes, whose complex frequencies ![]() $\omega$ are given by
$\omega$ are given by
where the coefficients ![]() $A_{T} = A_{T}(k_{\|} \rho _e,k_{\perp } \rho _e,\eta _e^T \beta _e)$,
$A_{T} = A_{T}(k_{\|} \rho _e,k_{\perp } \rho _e,\eta _e^T \beta _e)$, ![]() $B_{T} = B_{T}(k_{\|} \rho _e,k_{\perp } \rho _e,\eta _e^T \beta _e)$ and
$B_{T} = B_{T}(k_{\|} \rho _e,k_{\perp } \rho _e,\eta _e^T \beta _e)$ and ![]() $C_{T} = C_{T}(k_{\|} \rho _e,k_{\perp } \rho _e,\eta _e^T \beta _e)$ are composed of the sums and products of the special functions defined in (2.122), and also other special functions defined in Appendix G.3. For a given wavenumber, we can use (3.12) to calculate the growth rates of any unstable oblique modes – and, in particular, demonstrate that positive growth rates are present for certain values of
$C_{T} = C_{T}(k_{\|} \rho _e,k_{\perp } \rho _e,\eta _e^T \beta _e)$ are composed of the sums and products of the special functions defined in (2.122), and also other special functions defined in Appendix G.3. For a given wavenumber, we can use (3.12) to calculate the growth rates of any unstable oblique modes – and, in particular, demonstrate that positive growth rates are present for certain values of ![]() $\eta _e^T$. When they do exist, (3.12) suggests that they will have the typical size
$\eta _e^T$. When they do exist, (3.12) suggests that they will have the typical size ![]() $\gamma \sim \varOmega _e/\beta _e \sim \eta _e^T \varOmega _e$ when
$\gamma \sim \varOmega _e/\beta _e \sim \eta _e^T \varOmega _e$ when ![]() $k \rho _e \sim 1$ and
$k \rho _e \sim 1$ and ![]() $\eta _e^T \beta _e \sim 1$.
$\eta _e^T \beta _e \sim 1$.
For ![]() $\eta _e^T > 0$, we find that both modes (3.12) are damped; for
$\eta _e^T > 0$, we find that both modes (3.12) are damped; for ![]() $\eta _e^T < 0$, one mode is damped for all wavenumbers, but the other is not. Figure 4 shows the maximum (positive) growth rate
$\eta _e^T < 0$, one mode is damped for all wavenumbers, but the other is not. Figure 4 shows the maximum (positive) growth rate ![]() $\gamma$ (normalised to
$\gamma$ (normalised to ![]() $\varOmega _e/\beta _e$) of this mode at a fixed value of
$\varOmega _e/\beta _e$) of this mode at a fixed value of ![]() $\eta _e^T$, for a range of
$\eta _e^T$, for a range of ![]() $\beta _e$. The growth rate is calculated by evaluating the imaginary part of (3.12) at a given wavenumber. For
$\beta _e$. The growth rate is calculated by evaluating the imaginary part of (3.12) at a given wavenumber. For ![]() $-\eta _e^T < 1/\beta _e$, the mode of interest is damped for most wavenumbers, except for a small region of wavenumbers quasi-parallel to the magnetic field: in this region, there is a very small growth rate
$-\eta _e^T < 1/\beta _e$, the mode of interest is damped for most wavenumbers, except for a small region of wavenumbers quasi-parallel to the magnetic field: in this region, there is a very small growth rate ![]() $\gamma \ll \varOmega _e/\beta _e$ (figure 4a). This finding is consistent with the exponentially small growth rates found for the parallel whistler modes (see (3.8)). When
$\gamma \ll \varOmega _e/\beta _e$ (figure 4a). This finding is consistent with the exponentially small growth rates found for the parallel whistler modes (see (3.8)). When ![]() $-\eta _e^T \sim 1/\beta _e$, there is a marked change in behaviour: a larger region of unstable modes appears, with
$-\eta _e^T \sim 1/\beta _e$, there is a marked change in behaviour: a larger region of unstable modes appears, with ![]() $\gamma \sim \varOmega _e/\beta _e$, at wavenumbers
$\gamma \sim \varOmega _e/\beta _e$, at wavenumbers ![]() $k \rho _e \sim 1$ (figure 4b,c). The growth rate is the largest for parallel modes – but there also exist oblique modes with
$k \rho _e \sim 1$ (figure 4b,c). The growth rate is the largest for parallel modes – but there also exist oblique modes with ![]() $k_{\bot } \lesssim k_{\|}$ whose growth rate is close to the peak growth rate. For example, for
$k_{\bot } \lesssim k_{\|}$ whose growth rate is close to the peak growth rate. For example, for ![]() $\eta _e^T \beta _e = -4$, we find that the growth rate of the fastest-growing mode with a wavevector angle
$\eta _e^T \beta _e = -4$, we find that the growth rate of the fastest-growing mode with a wavevector angle ![]() $\theta = 10^{\circ }$ is only
$\theta = 10^{\circ }$ is only ![]() ${\sim }2\,\%$ smaller than the fastest-growing parallel mode; for a wavevector angle
${\sim }2\,\%$ smaller than the fastest-growing parallel mode; for a wavevector angle ![]() $\theta = 20^{\circ }$, the reduction is by
$\theta = 20^{\circ }$, the reduction is by ![]() ${\sim }6\,\%$; and for
${\sim }6\,\%$; and for ![]() $\theta = 30^{\circ }$, the reduction is by
$\theta = 30^{\circ }$, the reduction is by ![]() ${\sim }20\,\%$. Finally, if
${\sim }20\,\%$. Finally, if ![]() $-\eta _e^T \gg 1/\beta _e$, there exists a extended region of unstable modes, with
$-\eta _e^T \gg 1/\beta _e$, there exists a extended region of unstable modes, with ![]() $1 \lesssim k \rho _e \lesssim |\eta _e^T \beta _e|^{1/3}$, and
$1 \lesssim k \rho _e \lesssim |\eta _e^T \beta _e|^{1/3}$, and ![]() $\gamma \sim |\eta _e^T \varOmega _e|$ (figure 4d). Again, the peak growth rate is at
$\gamma \sim |\eta _e^T \varOmega _e|$ (figure 4d). Again, the peak growth rate is at ![]() $k_{\perp } = 0$, but oblique modes also have a significant growth rate (for unstable modes with
$k_{\perp } = 0$, but oblique modes also have a significant growth rate (for unstable modes with ![]() $\theta = 30^{\circ }$, the reduction in the largest growth rate compared with the fastest-growing parallel mode is only by
$\theta = 30^{\circ }$, the reduction in the largest growth rate compared with the fastest-growing parallel mode is only by ![]() ${\sim }4\,\%$). Most of the unstable modes have a non-zero real frequency: for
${\sim }4\,\%$). Most of the unstable modes have a non-zero real frequency: for ![]() $-\eta _e^T \sim 1/\beta _e$,
$-\eta _e^T \sim 1/\beta _e$, ![]() $\omega \sim \gamma$ (figure 4e), while for
$\omega \sim \gamma$ (figure 4e), while for ![]() $-\eta _e^T \gg 1/\beta _e$,
$-\eta _e^T \gg 1/\beta _e$, ![]() $\omega \gg \gamma$ for
$\omega \gg \gamma$ for ![]() $k \rho _e \gg 1$ (figure 4f). Note, however, that in the latter case there exists a band of wavenumbers at which there is no real frequency.
$k \rho _e \gg 1$ (figure 4f). Note, however, that in the latter case there exists a band of wavenumbers at which there is no real frequency.

Figure 4. Oblique CET whistler instabilities. Maximum positive growth rates of unstable whistler modes whose instability is driven by the electron-temperature-gradient term in CE distribution function (3.1a), at arbitrary wavevectors with respect to the background magnetic field. The growth rates of the modes are calculated by taking the imaginary part of (3.12), where coefficients ![]() $A_{T}$,
$A_{T}$, ![]() $B_{T}$ and
$B_{T}$ and ![]() $C_{T}$ are known functions of the wavevector. The growth rates are calculated on a
$C_{T}$ are known functions of the wavevector. The growth rates are calculated on a ![]() $400^2$ grid, with equal logarithmic spacing in both perpendicular and parallel directions between the minimum and maximum wavenumbers. The resulting growth rates, when normalised as
$400^2$ grid, with equal logarithmic spacing in both perpendicular and parallel directions between the minimum and maximum wavenumbers. The resulting growth rates, when normalised as ![]() $\gamma \beta _e/\varOmega _e$, are functions of the dimensionless quantity
$\gamma \beta _e/\varOmega _e$, are functions of the dimensionless quantity ![]() $\eta _e^{T} \beta _e$; (a)
$\eta _e^{T} \beta _e$; (a) ![]() $\eta _e^{T} \beta _e = -0.5$, (b)
$\eta _e^{T} \beta _e = -0.5$, (b) ![]() $\eta _e^{T} \beta _e = -4$. (c) Same as (b) but with normalisation
$\eta _e^{T} \beta _e = -4$. (c) Same as (b) but with normalisation ![]() $\gamma /|\eta _e^{T}| \varOmega _e$. (d) Same as (c), but with
$\gamma /|\eta _e^{T}| \varOmega _e$. (d) Same as (c), but with ![]() $\eta _e^{T} \beta _e = -100$. (e) Ratio of growth rate to absolute value of real frequency for unstable modes for
$\eta _e^{T} \beta _e = -100$. (e) Ratio of growth rate to absolute value of real frequency for unstable modes for ![]() $\eta _e^{T} \beta _e = -4$. ( f) Same as (e), but with
$\eta _e^{T} \beta _e = -4$. ( f) Same as (e), but with ![]() $\eta _e^{T} \beta _e = -100$.
$\eta _e^{T} \beta _e = -100$.
In summary, we have (re-)established that the fastest-growing modes of the CET whistler instability are parallel to the magnetic field; however, we have shown semi-analytically (a novel result of this work) that the growth of oblique perturbations can be almost as large. This result is of some significance, because it has been argued that oblique whistler modes are necessary for the instability to scatter heat-carrying electrons efficiently (see, e.g. Komarov et al. Reference Komarov, Schekochihin, Churazov and Spitkovsky2018). It was proposed previously that such modes could arise from modifications to the CET electron-temperature-gradient terms induced by the unstable parallel whistler modes rendering the oblique modes the fastest-growing ones; our calculations suggest that it would only a require a small change to the CET whistler growth rates for this to be realised.
As a further aside, we observe that in a plasma with sufficiently high plasma ![]() $\beta _e$, these oblique modes are in fact closer in nature to KAWs than to whistler waves. Whistler waves are characterised as having effectively immobile ions (
$\beta _e$, these oblique modes are in fact closer in nature to KAWs than to whistler waves. Whistler waves are characterised as having effectively immobile ions (![]() $\omega \gg k_{\bot } v_{\mathrm {th}i}$), while KAWs have warm ions (
$\omega \gg k_{\bot } v_{\mathrm {th}i}$), while KAWs have warm ions (![]() $\omega \ll k_{\bot } v_{\mathrm {th}i}$); as a consequence, whistler waves have a negligible density perturbation (
$\omega \ll k_{\bot } v_{\mathrm {th}i}$); as a consequence, whistler waves have a negligible density perturbation (![]() $\delta n_e \ll Z_i e n_{e} \varphi /T_i$, where
$\delta n_e \ll Z_i e n_{e} \varphi /T_i$, where ![]() $\varphi$ is the electrostatic potential associated with the wave), while KAWs do not:
$\varphi$ is the electrostatic potential associated with the wave), while KAWs do not: ![]() $\delta n_e \approx Z_i e n_{e} {\varphi }/T_i$ (Boldyrev et al. Reference Boldyrev, Horaites, Xia and Perez2013). In a
$\delta n_e \approx Z_i e n_{e} {\varphi }/T_i$ (Boldyrev et al. Reference Boldyrev, Horaites, Xia and Perez2013). In a ![]() $\beta _e \sim 1$ plasma for
$\beta _e \sim 1$ plasma for ![]() $k_{\bot } \gtrsim k_{\|}$, the real frequency of whistler modes satisfies
$k_{\bot } \gtrsim k_{\|}$, the real frequency of whistler modes satisfies ![]() $\omega /k_{\bot } v_{\mathrm {th}i} \sim k_{\|} \rho _i/\beta _e \sim k_{\|} \rho _i$; thus, we conclude from our above considerations that the two waves must operate in different regions of wavenumber space, viz.
$\omega /k_{\bot } v_{\mathrm {th}i} \sim k_{\|} \rho _i/\beta _e \sim k_{\|} \rho _i$; thus, we conclude from our above considerations that the two waves must operate in different regions of wavenumber space, viz. ![]() $k_{\|} \rho _i \ll 1$,
$k_{\|} \rho _i \ll 1$, ![]() $k_{\bot } \rho _i > 1$ for KAWs, and
$k_{\bot } \rho _i > 1$ for KAWs, and ![]() $k_{\|} \rho _i \gg 1$ for whistlers. However, for
$k_{\|} \rho _i \gg 1$ for whistlers. However, for ![]() $\beta _e \gtrsim \mu _e^{-1/2}$ (where
$\beta _e \gtrsim \mu _e^{-1/2}$ (where ![]() $\mu _e = m_e/m_i$) and
$\mu _e = m_e/m_i$) and ![]() $k_{\bot } \sim k_{\|} \gg \rho _i^{-1}$, the frequency of whistler waves is too low for
$k_{\bot } \sim k_{\|} \gg \rho _i^{-1}$, the frequency of whistler waves is too low for ![]() $\omega \gg k_{\bot } v_{\mathrm {th}i}$ to be satisfied whilst also maintaining
$\omega \gg k_{\bot } v_{\mathrm {th}i}$ to be satisfied whilst also maintaining ![]() $k_{\|} \rho _e \ll 1$. Instead, the ions participate in the wave mechanism, and
$k_{\|} \rho _e \ll 1$. Instead, the ions participate in the wave mechanism, and ![]() $\delta n_e \approx -Z_i e n_{e} {\varphi }/T_i$ (see Appendix H.2).
$\delta n_e \approx -Z_i e n_{e} {\varphi }/T_i$ (see Appendix H.2).
For further discussion of the physics of the whistler instability (as well as its nonlinear evolution), see Komarov et al. (Reference Komarov, Schekochihin, Churazov and Spitkovsky2018) and the other references given at the beginning of § 3.3.1.
3.3.3. Slow-(hydromagnetic)-wave instability
Although parallel ion heat fluxes in a classical, collisional plasma are typically much weaker than electron heat fluxes, they can still act as a free-energy source for instabilities, by introducing anisotropy to the ion distribution function (3.1b) (i.e. the CE ion-temperature-gradient term). Furthermore, anisotropy in the ion distribution function can enable the instability of plasma modes that are not destabilised by the CE electron-temperature-gradient term. This exact situation is realised in the CET slow-hydromagnetic-wave instability, in which a sufficiently large CET ion-temperature-gradient term counteracts the effect of ion-cyclotron damping on slow hydromagnetic waves. The slow hydromagnetic wave (or slow wave) (Rogister Reference Rogister1971; Foote & Kulsrud Reference Foote and Kulsrud1979) is the left-hand-polarised quasi-parallel electromagnetic mode in high-![]() $\beta$ plasma; it exists for parallel wavenumbers
$\beta$ plasma; it exists for parallel wavenumbers ![]() $k_{\|}$ that satisfy
$k_{\|}$ that satisfy ![]() $\beta _i^{-1/2} \ll k_{\|} \rho _i \lesssim 1$, and has a characteristic frequency
$\beta _i^{-1/2} \ll k_{\|} \rho _i \lesssim 1$, and has a characteristic frequency ![]() $\omega \approx 2 \varOmega _i/\beta _i$. To the authors’ knowledge, no instability of the slow wave due to the ion heat flux has previously been reported. The instability's mechanism is analogous to the CET whistler instability: the slow waves drain energy from ions with parallel velocities
$\omega \approx 2 \varOmega _i/\beta _i$. To the authors’ knowledge, no instability of the slow wave due to the ion heat flux has previously been reported. The instability's mechanism is analogous to the CET whistler instability: the slow waves drain energy from ions with parallel velocities ![]() $v_{\|} = \pm \varOmega _i/k_{\|}$ via gyroresonant wave–particle interactions. For an anti-parallel ion-temperature gradient (i.e.
$v_{\|} = \pm \varOmega _i/k_{\|}$ via gyroresonant wave–particle interactions. For an anti-parallel ion-temperature gradient (i.e. ![]() $\boldsymbol {\nabla }_{\|} T_i < 0$, so
$\boldsymbol {\nabla }_{\|} T_i < 0$, so ![]() $\eta _i < 0$), slow waves propagating down the temperature gradient are destabilised, while those propagating up the temperature gradient are not.
$\eta _i < 0$), slow waves propagating down the temperature gradient are destabilised, while those propagating up the temperature gradient are not.
As before, the slow-wave instability is most easily characterised in the subsidiary limit ![]() $k_{\bot } \rho _i \rightarrow 0$ (
$k_{\bot } \rho _i \rightarrow 0$ (![]() $k = k_{\|}$). Under the ordering
$k = k_{\|}$). Under the ordering ![]() $k_{\|} \rho _i \sim 1$, the real frequency
$k_{\|} \rho _i \sim 1$, the real frequency ![]() $\varpi$ and growth rate
$\varpi$ and growth rate ![]() $\gamma$ are given by (see Appendix J.4.1)
$\gamma$ are given by (see Appendix J.4.1)
 $$\begin{align} \frac{\varpi}{\varOmega_i} &= \eta_i \left(\frac{k_{\|} \rho_i}{4}-\frac{1}{2 k_\| \rho_i}\right) - \frac{k_{\|}^2 \rho_i^2 \left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_i}\right)} + k_{\|} \rho_i\right] \left(\eta_i/4 + k_\| \rho_i/\beta_i\right) }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_i}\right)} + k_{\|} \rho_i\right]^2 + {\rm \pi}\exp{\left(-{2}/{k_\|^2 \rho_i^2}\right)}} , \end{align}$$
$$\begin{align} \frac{\varpi}{\varOmega_i} &= \eta_i \left(\frac{k_{\|} \rho_i}{4}-\frac{1}{2 k_\| \rho_i}\right) - \frac{k_{\|}^2 \rho_i^2 \left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_i}\right)} + k_{\|} \rho_i\right] \left(\eta_i/4 + k_\| \rho_i/\beta_i\right) }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_i}\right)} + k_{\|} \rho_i\right]^2 + {\rm \pi}\exp{\left(-{2}/{k_\|^2 \rho_i^2}\right)}} , \end{align}$$ $$\begin{align}\frac{\gamma}{\varOmega_i} &={-} \frac{\sqrt{\rm \pi} k_{\|}^2 \rho_i^2 \left(\eta_i/4 + k_\| \rho_i/\beta_i\right) }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_i}\right)} + k_{\|} \rho_i\right]^2 \exp{\left({1}/{k_\|^2 \rho_i^2}\right)}+ {\rm \pi}\exp{\left(-{1}/{k_\|^2 \rho_i^2}\right)}} . \end{align}$$
$$\begin{align}\frac{\gamma}{\varOmega_i} &={-} \frac{\sqrt{\rm \pi} k_{\|}^2 \rho_i^2 \left(\eta_i/4 + k_\| \rho_i/\beta_i\right) }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_i}\right)} + k_{\|} \rho_i\right]^2 \exp{\left({1}/{k_\|^2 \rho_i^2}\right)}+ {\rm \pi}\exp{\left(-{1}/{k_\|^2 \rho_i^2}\right)}} . \end{align}$$
The CET electron-temperature-gradient term does not appear because its contributions to the frequency and growth rate are much smaller than the equivalent contributions of the CET ion-temperature-gradient term at ![]() $k_{\|} \rho _i \sim 1$. Plots of
$k_{\|} \rho _i \sim 1$. Plots of ![]() $\varpi = \varpi (k_{\|})$ and
$\varpi = \varpi (k_{\|})$ and ![]() $\gamma = \gamma (k_{\|})$ for different values of
$\gamma = \gamma (k_{\|})$ for different values of ![]() $\eta _i \beta _i < 0$ are shown in figure 5.
$\eta _i \beta _i < 0$ are shown in figure 5.

Figure 5. Parallel CET slow-hydromagnetic-wave instability. Dispersion curves of slow hydromagnetic waves whose instability is driven by the ion-temperature-gradient term in the CE distribution function (3.1b), for wavevectors co-parallel with the background magnetic field (viz. ![]() $\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The frequency (solid blue) and growth rates (solid red) of the modes are calculated using (3.13a) and (3.13b), respectively. The resulting frequencies and growth rates, when normalised as
$\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The frequency (solid blue) and growth rates (solid red) of the modes are calculated using (3.13a) and (3.13b), respectively. The resulting frequencies and growth rates, when normalised as ![]() $\gamma \beta _i/\varOmega _i$, are functions of the dimensionless quantity
$\gamma \beta _i/\varOmega _i$, are functions of the dimensionless quantity ![]() $\eta _i \beta _i$; we show the dispersion curves for three different values of
$\eta _i \beta _i$; we show the dispersion curves for three different values of ![]() $\eta _i \beta _i$. The approximations (3.14) and (3.15) for the frequency (dotted blue) and growth rate (dotted red) in the limit
$\eta _i \beta _i$. The approximations (3.14) and (3.15) for the frequency (dotted blue) and growth rate (dotted red) in the limit ![]() $k_{\|} \rho _i \ll 1$ are also plotted, as are the approximations (3.18a) and (3.18b) for the frequency (dashed blue) and growth rate (dashed red) in the limit
$k_{\|} \rho _i \ll 1$ are also plotted, as are the approximations (3.18a) and (3.18b) for the frequency (dashed blue) and growth rate (dashed red) in the limit ![]() $k_{\|} \rho _i \gg 1$.
$k_{\|} \rho _i \gg 1$.
As with the CET whistler instability, we can derive simple expressions for the peak growth rate (and the wavenumber associated with that growth rate) in subsidiary limits.
First, ordering ![]() $k_{\|} \rho _i \sim |\eta _i| \beta _i/4 \ll 1$ so that the destabilising
$k_{\|} \rho _i \sim |\eta _i| \beta _i/4 \ll 1$ so that the destabilising ![]() $\eta _i$ terms and the stabilising ion FLR terms are the same order, we find that the real frequency (3.13a) becomes
$\eta _i$ terms and the stabilising ion FLR terms are the same order, we find that the real frequency (3.13a) becomes
which is precisely that of the slow hydromagnetic wave, with first-order FLR corrections included (Foote & Kulsrud Reference Foote and Kulsrud1979). For ![]() $\eta _i < 0$ and
$\eta _i < 0$ and ![]() $k_{\|} \rho _i < |\eta _i| \beta _i/4$, the growth rate (3.13b) is positive:
$k_{\|} \rho _i < |\eta _i| \beta _i/4$, the growth rate (3.13b) is positive:
 \begin{equation} \gamma \approx{-} \frac{4 \sqrt{\rm \pi}}{k_\|^4 \rho_i^4} \left(\frac{\eta_i}{4} + \frac{k_{\|} \rho_i}{\beta_i}\right)\exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} \varOmega_i . \end{equation}
\begin{equation} \gamma \approx{-} \frac{4 \sqrt{\rm \pi}}{k_\|^4 \rho_i^4} \left(\frac{\eta_i}{4} + \frac{k_{\|} \rho_i}{\beta_i}\right)\exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} \varOmega_i . \end{equation}
The maximum growth rate (which is exponentially small in ![]() $\eta _i \beta _i/4 \ll 1$) is
$\eta _i \beta _i/4 \ll 1$) is
achieved at the parallel wavenumber
In the opposite limit, ![]() $k_{\|} \rho _i \sim (|\eta _i| \beta _i/4)^{1/3} \gg 1$, we obtain
$k_{\|} \rho _i \sim (|\eta _i| \beta _i/4)^{1/3} \gg 1$, we obtain
 $$\begin{align}\gamma &\approx{-}\sqrt{\rm \pi} \left[\frac{\eta_i}{4} \beta_i\left(1-\frac{{\rm \pi}-3}{k_{\|}^2 \rho_i^2}\right) + k_{\|} \rho_i \right] \frac{\varOmega_i}{\beta_i} . \end{align}$$
$$\begin{align}\gamma &\approx{-}\sqrt{\rm \pi} \left[\frac{\eta_i}{4} \beta_i\left(1-\frac{{\rm \pi}-3}{k_{\|}^2 \rho_i^2}\right) + k_{\|} \rho_i \right] \frac{\varOmega_i}{\beta_i} . \end{align}$$The maximum positive growth rate is
realised for ![]() $\eta _i < 0$ at the parallel wavenumber
$\eta _i < 0$ at the parallel wavenumber
 \begin{equation} k_{\|} \rho_i \approx \left(\frac{{\rm \pi} -3}{2}\right) ^{1/3} \left(|\eta_i|\beta_i\right)^{1/3} \approx 0.41 \left(|\eta_i|\beta_i\right)^{1/3} . \end{equation}
\begin{equation} k_{\|} \rho_i \approx \left(\frac{{\rm \pi} -3}{2}\right) ^{1/3} \left(|\eta_i|\beta_i\right)^{1/3} \approx 0.41 \left(|\eta_i|\beta_i\right)^{1/3} . \end{equation}
We note that, in contrast to the CET whistler instability, the real frequency of the fastest-growing unstable mode is smaller than its growth rate: ![]() $\omega _{\rm peak}/\gamma _{\rm max} \approx 0.36 (|\eta _i|\beta _i)^{-1/3}$.
$\omega _{\rm peak}/\gamma _{\rm max} \approx 0.36 (|\eta _i|\beta _i)^{-1/3}$.
The approximate expressions (3.14), (3.15), (3.18a) and (3.18b) for the frequency and growth rate in the limits ![]() $k_{\|} \rho _i \ll 1$ and
$k_{\|} \rho _i \ll 1$ and ![]() $k_{\|} \rho _i \gg 1$, are plotted in figure 5, along with the exact results (3.13).
$k_{\|} \rho _i \gg 1$, are plotted in figure 5, along with the exact results (3.13).
As with the CET whistler instability, a general expression for the complex frequency of oblique ion CET instabilities can be derived in the form (see Appendix J.4)
 \begin{equation} \omega = \frac{\varOmega_i}{\beta_i} k_{\|} |\rho_i| \frac{-\tilde{B}_{T} \pm \sqrt{\tilde{B}_{T}^2 + 4\tilde{A}_{T}\tilde{C}_{T}}}{2 \tilde{A}_{T}} , \end{equation}
\begin{equation} \omega = \frac{\varOmega_i}{\beta_i} k_{\|} |\rho_i| \frac{-\tilde{B}_{T} \pm \sqrt{\tilde{B}_{T}^2 + 4\tilde{A}_{T}\tilde{C}_{T}}}{2 \tilde{A}_{T}} , \end{equation}
where ![]() $\tilde {A}_{T} = \tilde {A}_{T}(k_{\|} \rho _i,k_{\perp } \rho _i,\eta _i \beta _i)$,
$\tilde {A}_{T} = \tilde {A}_{T}(k_{\|} \rho _i,k_{\perp } \rho _i,\eta _i \beta _i)$, ![]() $\tilde {B}_{T} = \tilde {B}_{T}(k_{\|} \rho _i,k_{\perp } \rho _i,\eta _i \beta _i)$ and
$\tilde {B}_{T} = \tilde {B}_{T}(k_{\|} \rho _i,k_{\perp } \rho _i,\eta _i \beta _i)$ and ![]() $\tilde {C}_{T} = \tilde {C}_{T}(k_{\|} \rho _i,k_{\perp } \rho _i,\eta _i \beta _i)$ are again sums and products of various special mathematical functions defined in (2.122). Investigating such modes by evaluating (3.21) numerically for a range of wavenumbers (see figure 6), we find that, for
$\tilde {C}_{T} = \tilde {C}_{T}(k_{\|} \rho _i,k_{\perp } \rho _i,\eta _i \beta _i)$ are again sums and products of various special mathematical functions defined in (2.122). Investigating such modes by evaluating (3.21) numerically for a range of wavenumbers (see figure 6), we find that, for ![]() $\eta _i < 0$, there is one mode that is always damped and one that can be unstable. For
$\eta _i < 0$, there is one mode that is always damped and one that can be unstable. For ![]() $-\eta _i \lesssim 4/\beta _i$, the unstable modes are restricted to quasi-parallel modes (see figure 6a); for
$-\eta _i \lesssim 4/\beta _i$, the unstable modes are restricted to quasi-parallel modes (see figure 6a); for ![]() $-\eta _i \gtrsim 4/\beta _i$, there is a much broader spectrum of unstable modes (including oblique ones). The positive growth rates of the unstable mode are shown in figure 6(b) for
$-\eta _i \gtrsim 4/\beta _i$, there is a much broader spectrum of unstable modes (including oblique ones). The positive growth rates of the unstable mode are shown in figure 6(b) for ![]() $\eta _i \beta _i = -8$. The typical growth rate
$\eta _i \beta _i = -8$. The typical growth rate ![]() $\gamma$ satisfies
$\gamma$ satisfies ![]() $\gamma \sim \varOmega _i/\beta _i \sim \eta _i \varOmega _i$, as anticipated from (3.21). We also observe in figure 6(b) the existence of an unstable mode at quasi-perpendicular wavenumbers, which is discussed in § 3.3.4.
$\gamma \sim \varOmega _i/\beta _i \sim \eta _i \varOmega _i$, as anticipated from (3.21). We also observe in figure 6(b) the existence of an unstable mode at quasi-perpendicular wavenumbers, which is discussed in § 3.3.4.

Figure 6. Oblique CET ion-Larmor-scale instabilities. Maximum positive growth rates of unstable ion-Larmor-scale modes whose instability is driven by the CE ion-temperature-gradient term in the CE distribution function (3.1b), at arbitrary wavevectors with respect to the background magnetic field. The growth rates of all modes are calculated by taking the imaginary part of (3.21), with coefficients ![]() $\tilde {A}_{T}$,
$\tilde {A}_{T}$, ![]() $\tilde {B}_{T}$ and
$\tilde {B}_{T}$ and ![]() $\tilde {C}_{T}$ being known functions of the wavevector (see Appendix J.4). The growth rates are calculated on a
$\tilde {C}_{T}$ being known functions of the wavevector (see Appendix J.4). The growth rates are calculated on a ![]() $400^2$ grid, with logarithmic spacing in both perpendicular and parallel directions between the minimum and maximum wavenumber magnitudes. The resulting growth rates, when normalised as
$400^2$ grid, with logarithmic spacing in both perpendicular and parallel directions between the minimum and maximum wavenumber magnitudes. The resulting growth rates, when normalised as ![]() $\gamma \beta _i/\varOmega _i$, are functions of
$\gamma \beta _i/\varOmega _i$, are functions of ![]() $\eta _i \beta _i$; (a)
$\eta _i \beta _i$; (a) ![]() $\eta _i \beta _i = -2.5$, (b)
$\eta _i \beta _i = -2.5$, (b) ![]() $\eta _i \beta _i = -8$. The unstable
$\eta _i \beta _i = -8$. The unstable ![]() $k_{\|} \rho _i \ll k_{\perp } \rho _i \sim 1$ modes appearing in (b) are dealt with in § 3.3.4.
$k_{\|} \rho _i \ll k_{\perp } \rho _i \sim 1$ modes appearing in (b) are dealt with in § 3.3.4.
In summary, an ion-temperature gradient can destabilise ion-Larmor-scale, slow hydromagnetic waves via a similar mechanism to an electron-temperature gradient destabilising electron-Larmor-scale whistler waves. If ![]() $\beta _i \gg L_{T_i}/\lambda _i$, the characteristic growth rate of these modes is
$\beta _i \gg L_{T_i}/\lambda _i$, the characteristic growth rate of these modes is ![]() $\gamma \sim \lambda _i \varOmega _i/L_{T_i}$. Unstable modes whose wavevector is parallel to
$\gamma \sim \lambda _i \varOmega _i/L_{T_i}$. Unstable modes whose wavevector is parallel to ![]() $\boldsymbol {B}_0$ grow most rapidly, although the growth rate of (moderately) oblique modes is only somewhat smaller. While the CET whistler instability is faster growing than the CET slow-wave instability, both modes grow much more quickly than characteristic hydrodynamic time scales in a strongly magnetised plasma. In any conceivable saturation mechanism, the electron mode will adjust the electron heat flux, and the ion mode the ion heat flux. Thus, it seems likely that understanding the evolution (and ultimately, the saturation) of both instabilities would be necessary to model correctly the heat transport in a classical, collisional plasma that falls foul of the
$\boldsymbol {B}_0$ grow most rapidly, although the growth rate of (moderately) oblique modes is only somewhat smaller. While the CET whistler instability is faster growing than the CET slow-wave instability, both modes grow much more quickly than characteristic hydrodynamic time scales in a strongly magnetised plasma. In any conceivable saturation mechanism, the electron mode will adjust the electron heat flux, and the ion mode the ion heat flux. Thus, it seems likely that understanding the evolution (and ultimately, the saturation) of both instabilities would be necessary to model correctly the heat transport in a classical, collisional plasma that falls foul of the ![]() $\beta$-stabilisation condition.
$\beta$-stabilisation condition.
3.3.4. Long-wavelength kinetic-Alfvén-wave instability
The instability observed in figure 6(b) at wavevectors satisfying ![]() $k_{\|} \rho _i \ll k_{\perp } \rho _i \sim 1$ is different in nature to the slow-hydromagnetic-wave instability: it is an ion-temperature-gradient-driven instability of long-wavelength KAWs. Like the CET slow-wave instability, it operates on account of resonant wave–particle interactions that allow free energy to be drained from the anisotropy of the ion distribution function, which itself arises from the ion-temperature gradient. However, the gyroresonances
$k_{\|} \rho _i \ll k_{\perp } \rho _i \sim 1$ is different in nature to the slow-hydromagnetic-wave instability: it is an ion-temperature-gradient-driven instability of long-wavelength KAWs. Like the CET slow-wave instability, it operates on account of resonant wave–particle interactions that allow free energy to be drained from the anisotropy of the ion distribution function, which itself arises from the ion-temperature gradient. However, the gyroresonances ![]() $v_{\|} \approx \pm \varOmega _i/k_{\|}$ operate inefficiently for modes with
$v_{\|} \approx \pm \varOmega _i/k_{\|}$ operate inefficiently for modes with ![]() $k_{\|} \rho _i \ll 1$ in a CE plasma, because there are comparatively few particles with
$k_{\|} \rho _i \ll 1$ in a CE plasma, because there are comparatively few particles with ![]() $v_{\|} \gg v_{\mathrm {th}i}$; the dominant resonance is instead the Landau resonance
$v_{\|} \gg v_{\mathrm {th}i}$; the dominant resonance is instead the Landau resonance ![]() $v_{\|} = \omega /k_{\|}$. More specifically, KAWs with
$v_{\|} = \omega /k_{\|}$. More specifically, KAWs with ![]() $k_{\perp } \rho _i \gtrsim 1$, which are usually subject to strong Landau and Barnes damping (that is, the damping rate of the waves is comparable to their real frequency), can be destabilised if the (ion) plasma beta is sufficiently large:
$k_{\perp } \rho _i \gtrsim 1$, which are usually subject to strong Landau and Barnes damping (that is, the damping rate of the waves is comparable to their real frequency), can be destabilised if the (ion) plasma beta is sufficiently large: ![]() $\beta _i \gtrsim L_{T_i}/\lambda _i$. In figure 6(b), the peak growth rate of the CET KAW instability is smaller than that of the CET slow-hydromagnetic-wave instability by an order of magnitude; as will be shown below, this is, in fact, a generic feature of the instability.
$\beta _i \gtrsim L_{T_i}/\lambda _i$. In figure 6(b), the peak growth rate of the CET KAW instability is smaller than that of the CET slow-hydromagnetic-wave instability by an order of magnitude; as will be shown below, this is, in fact, a generic feature of the instability.
Similarly to quasi-parallel unstable modes, quasi-perpendicular ones such as unstable KAWs can be characterised analytically, allowing for a simple identification of unstable modes and their peak growth rates. It can be shown (see Appendix J.4.2) that, in the limit ![]() $k_{\|} \rho _i \ll 1$,
$k_{\|} \rho _i \ll 1$, ![]() $k_\perp \rho _i \sim 1$, the complex frequency of the low-frequency (
$k_\perp \rho _i \sim 1$, the complex frequency of the low-frequency (![]() $\omega \ll k_{\|} v_{\mathrm {th}i}$) modes in a plasma whose ion distribution function is (3.1b) is
$\omega \ll k_{\|} v_{\mathrm {th}i}$) modes in a plasma whose ion distribution function is (3.1b) is
 \begin{align} \frac{\omega}{k_{\|} v_{\mathrm{th}i}} & = \frac{\eta_i \mathcal{G}_i}{2 \left(1-\mathcal{F}_i\right)} + \frac{k_{{\perp}} \rho_i}{\beta_i \left(1-\mathcal{F}_i\right)^{2}} \left[ -\frac{\mathrm{i}\sqrt{\rm \pi}}{2} k_{{\perp}} \rho_i \left(\mathcal{F}_i + \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right)\right. \nonumber\\ & \left.\quad \pm \sqrt{1-\frac{\rm \pi}{4} \frac{k_{{\perp}}^2 \rho_i^2}{\beta_i} \bigg(\mathcal{F}_i + \sqrt{\frac{\mu_e Z_i^2}{\tau}}\bigg)^2 - \frac{\mathrm{i} \sqrt{\rm \pi} \eta_i \beta_i}{4} \frac{2 \mathcal{G}_i - \mathcal{F}_i\left(1 - \mathcal{F}_i\right)}{1-\mathcal{F}_i} } \right] , \end{align}
\begin{align} \frac{\omega}{k_{\|} v_{\mathrm{th}i}} & = \frac{\eta_i \mathcal{G}_i}{2 \left(1-\mathcal{F}_i\right)} + \frac{k_{{\perp}} \rho_i}{\beta_i \left(1-\mathcal{F}_i\right)^{2}} \left[ -\frac{\mathrm{i}\sqrt{\rm \pi}}{2} k_{{\perp}} \rho_i \left(\mathcal{F}_i + \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right)\right. \nonumber\\ & \left.\quad \pm \sqrt{1-\frac{\rm \pi}{4} \frac{k_{{\perp}}^2 \rho_i^2}{\beta_i} \bigg(\mathcal{F}_i + \sqrt{\frac{\mu_e Z_i^2}{\tau}}\bigg)^2 - \frac{\mathrm{i} \sqrt{\rm \pi} \eta_i \beta_i}{4} \frac{2 \mathcal{G}_i - \mathcal{F}_i\left(1 - \mathcal{F}_i\right)}{1-\mathcal{F}_i} } \right] , \end{align}
where ![]() $\mathcal {F}_i \equiv \mathcal {F}(k_{\perp } \rho _i)$,
$\mathcal {F}_i \equiv \mathcal {F}(k_{\perp } \rho _i)$, ![]() $\mathcal {G}_i \equiv \mathcal {G}(k_{\perp } \rho _i)$ and
$\mathcal {G}_i \equiv \mathcal {G}(k_{\perp } \rho _i)$ and
In a Maxwellian plasma (i.e. when ![]() $\eta _i = 0$), (3.22) becomes
$\eta _i = 0$), (3.22) becomes
 \begin{align} \frac{\omega}{k_{\|} v_{\mathrm{th}i}} & = \frac{1}{\left(1-\mathcal{F}_i\right)^{2}} \left[ -\frac{\mathrm{i}\sqrt{\rm \pi}}{2} \frac{k_{{\perp}}^2 \rho_i^2}{\beta_i} \left(\mathcal{F}_i + \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right)\right. \nonumber\\ &\quad \left.\pm \sqrt{\frac{k_{{\perp}}^2 \rho_i^2}{\beta_i^2}-\frac{\rm \pi}{4} \frac{k_{{\perp}}^4 \rho_i^4}{\beta_i^2} \left(\mathcal{F}_i + \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right)^2} \right] . \end{align}
\begin{align} \frac{\omega}{k_{\|} v_{\mathrm{th}i}} & = \frac{1}{\left(1-\mathcal{F}_i\right)^{2}} \left[ -\frac{\mathrm{i}\sqrt{\rm \pi}}{2} \frac{k_{{\perp}}^2 \rho_i^2}{\beta_i} \left(\mathcal{F}_i + \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right)\right. \nonumber\\ &\quad \left.\pm \sqrt{\frac{k_{{\perp}}^2 \rho_i^2}{\beta_i^2}-\frac{\rm \pi}{4} \frac{k_{{\perp}}^4 \rho_i^4}{\beta_i^2} \left(\mathcal{F}_i + \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right)^2} \right] . \end{align}
In the subsidiary limit ![]() $k_{\perp } \rho _i \gg 1$, we recover
$k_{\perp } \rho _i \gg 1$, we recover ![]() $\omega \approx \pm k_{\|} v_{\mathrm {th}i} k_{\perp } \rho _i/\beta _i$, which is the well-known dispersion relation of a KAW (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Boldyrev et al. Reference Boldyrev, Horaites, Xia and Perez2013; Kunz et al. Reference Kunz, Abel, Klein and Schekochihin2018).
$\omega \approx \pm k_{\|} v_{\mathrm {th}i} k_{\perp } \rho _i/\beta _i$, which is the well-known dispersion relation of a KAW (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Boldyrev et al. Reference Boldyrev, Horaites, Xia and Perez2013; Kunz et al. Reference Kunz, Abel, Klein and Schekochihin2018).
For ![]() $\eta _i \neq 0$, we find that, for modes with a positive propagation direction with respect to the background magnetic field (viz.
$\eta _i \neq 0$, we find that, for modes with a positive propagation direction with respect to the background magnetic field (viz. ![]() $k_{\|} > 0$), there is an instability provided
$k_{\|} > 0$), there is an instability provided
 \begin{equation} \eta_i \lesssim -3.14 \left(1 + 6.5 \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right) \beta_i^{{-}1} , \end{equation}
\begin{equation} \eta_i \lesssim -3.14 \left(1 + 6.5 \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right) \beta_i^{{-}1} , \end{equation}
with the perpendicular wavenumber ![]() $k_{\perp } \rho _i$ of the fastest-growing unstable mode at fixed
$k_{\perp } \rho _i$ of the fastest-growing unstable mode at fixed ![]() $k_{\|}$ just beyond this threshold being approximately given by
$k_{\|}$ just beyond this threshold being approximately given by
 \begin{equation} k_{{\perp}} \rho_i \approx 1.77 \left(1 - 3.4 \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right) . \end{equation}
\begin{equation} k_{{\perp}} \rho_i \approx 1.77 \left(1 - 3.4 \sqrt{\frac{\mu_e Z_i^2}{\tau}}\right) . \end{equation}
Figure 7 shows the real frequency and growth rate of such modes at three different (negative) values of ![]() $\eta _i \beta _i$. As
$\eta _i \beta _i$. As ![]() $\eta _i$ is decreased beyond the threshold, modes over an increasingly large range of perpendicular wavenumbers are destabilised at both super- and sub-ion-Larmor scales. Indeed, in the limit
$\eta _i$ is decreased beyond the threshold, modes over an increasingly large range of perpendicular wavenumbers are destabilised at both super- and sub-ion-Larmor scales. Indeed, in the limit ![]() $|\eta _i| \beta _i \gg 1$, the peak growth rate
$|\eta _i| \beta _i \gg 1$, the peak growth rate ![]() $\gamma _{\rm max}$ (for a fixed
$\gamma _{\rm max}$ (for a fixed ![]() $k_{\|}$) occurs at a perpendicular wavenumber
$k_{\|}$) occurs at a perpendicular wavenumber ![]() $k_{\perp } \rho _i < 1$, which decreases as
$k_{\perp } \rho _i < 1$, which decreases as ![]() $|\eta _i| \beta _i$ increases. Such modes are, in fact, no longer well described physically as KAWs; their analogues in a Maxwellian plasma are Barnes-damped, non-propagating slow modes.
$|\eta _i| \beta _i$ increases. Such modes are, in fact, no longer well described physically as KAWs; their analogues in a Maxwellian plasma are Barnes-damped, non-propagating slow modes.

Figure 7. Quasi-perpendicular CET KAW instability. Dispersion curves of unstable KAWs whose instability is driven by the ion-temperature-gradient term in the CE distribution function (3.1b), for wavevectors that are almost perpendicular to the background magnetic field (viz. ![]() $k_{\perp } \gg k_{\|}$). The frequency (blue) and growth rates (red) of unstable modes are calculated at (small) fixed values of
$k_{\perp } \gg k_{\|}$). The frequency (blue) and growth rates (red) of unstable modes are calculated at (small) fixed values of ![]() $k_{\|} \rho _i$ from the real and imaginary parts of (3.21); the solid curves are calculated for
$k_{\|} \rho _i$ from the real and imaginary parts of (3.21); the solid curves are calculated for ![]() $k_{\|} \rho _i = 0.35$, while the dashed curves are for
$k_{\|} \rho _i = 0.35$, while the dashed curves are for ![]() $k_{\|} \rho _i = 0.05$. The resulting frequencies and growth rates, when normalised as
$k_{\|} \rho _i = 0.05$. The resulting frequencies and growth rates, when normalised as ![]() $\gamma \beta _i/k_{\|} v_{\mathrm {th}i}$, are functions of the dimensionless quantity
$\gamma \beta _i/k_{\|} v_{\mathrm {th}i}$, are functions of the dimensionless quantity ![]() $\eta _i \beta _i$; we show the dispersion curves for three different values of
$\eta _i \beta _i$; we show the dispersion curves for three different values of ![]() $\eta _i \beta _i$. The frequency (dotted blue) and growth rate (dotted red) in the limit
$\eta _i \beta _i$. The frequency (dotted blue) and growth rate (dotted red) in the limit ![]() $k_{\|} \rho _i \ll 1$, which are calculated by taking the real and imaginary parts of (3.22), are also plotted.
$k_{\|} \rho _i \ll 1$, which are calculated by taking the real and imaginary parts of (3.22), are also plotted.
Although it is possible to characterise analytically the peak growth rate of the unstable modes (and the perpendicular wavenumber at which such growth is attained) in the limit ![]() $k_{\|} \rho _i \ll 1$ by analysing (3.22), such estimates do not capture accurately the behaviour of the fastest-growing modes across all wavevectors, because these fastest-growing modes occur at finite values of
$k_{\|} \rho _i \ll 1$ by analysing (3.22), such estimates do not capture accurately the behaviour of the fastest-growing modes across all wavevectors, because these fastest-growing modes occur at finite values of ![]() $k_{\|} \rho _i$; at such values, the dependence of the frequency and growth rate on
$k_{\|} \rho _i$; at such values, the dependence of the frequency and growth rate on ![]() $k_{\perp } \rho _i$ departs somewhat from (3.22) (see figure 7). Instead, we find numerically that, for
$k_{\perp } \rho _i$ departs somewhat from (3.22) (see figure 7). Instead, we find numerically that, for ![]() $\eta _i \beta _i \lesssim -6$,
$\eta _i \beta _i \lesssim -6$,
independent of the specific value of either ![]() $\eta _i$ or
$\eta _i$ or ![]() $\beta _i$. For values of
$\beta _i$. For values of ![]() $k_{\|} \rho _i$ that are larger than
$k_{\|} \rho _i$ that are larger than ![]() $(k_{\|} \rho _i)_{\rm peak}$, the instability is quenched. It is clear that, in comparison with the slow-hydromagnetic-wave instability, the growth rate of the fastest-growing perpendicular modes is small (see (3.18)). This difference can be attributed to the fact that, for unstable modes in the limit
$(k_{\|} \rho _i)_{\rm peak}$, the instability is quenched. It is clear that, in comparison with the slow-hydromagnetic-wave instability, the growth rate of the fastest-growing perpendicular modes is small (see (3.18)). This difference can be attributed to the fact that, for unstable modes in the limit ![]() $|\eta _i| \beta _i \gg 1$,
$|\eta _i| \beta _i \gg 1$, ![]() $\gamma _{\rm max} \sim |\eta _i| k_{\|} \rho _i \varOmega _i$ and the value of
$\gamma _{\rm max} \sim |\eta _i| k_{\|} \rho _i \varOmega _i$ and the value of ![]() $k_{\|} \rho _i$ at which maximum growth is achieved is still rather small compared with unity. We conclude that the instability of slow hydromagnetic waves that are driven by an ion-temperature gradient is likely to be more significant than the analogous instability of quasi-perpendicular/KAW modes.
$k_{\|} \rho _i$ at which maximum growth is achieved is still rather small compared with unity. We conclude that the instability of slow hydromagnetic waves that are driven by an ion-temperature gradient is likely to be more significant than the analogous instability of quasi-perpendicular/KAW modes.
4. CES (Chapman–Enskog, shear-driven) microinstabilities
4.1. Form of CE distribution function
Next, we consider the non-Maxwellian terms of the CE distribution arising from bulk-flow gradients. If we set ![]() $\eta _s = 0$ for both ions and electrons (viz. neglecting both temperature gradients and electron–ion drifts), the CE distribution functions (2.8) for both species become
$\eta _s = 0$ for both ions and electrons (viz. neglecting both temperature gradients and electron–ion drifts), the CE distribution functions (2.8) for both species become
 \begin{equation} f_{s0}(v_{\|},v_{\bot}) = \frac{n_{s0}}{v_{\mathrm{th}s}^3 {\rm \pi}^{3/2}} \exp \left(-\tilde{v}_{s}^2\right) \left[1 - \epsilon_s \left(\frac{v_{\|}^2}{v_{\mathrm{th}s}^2}- \frac{v_{\bot}^2}{2 v_{\mathrm{th}s}^2} \right)\right] , \end{equation}
\begin{equation} f_{s0}(v_{\|},v_{\bot}) = \frac{n_{s0}}{v_{\mathrm{th}s}^3 {\rm \pi}^{3/2}} \exp \left(-\tilde{v}_{s}^2\right) \left[1 - \epsilon_s \left(\frac{v_{\|}^2}{v_{\mathrm{th}s}^2}- \frac{v_{\bot}^2}{2 v_{\mathrm{th}s}^2} \right)\right] , \end{equation}
where we have again chosen the isotropic functions ![]() $C_s(\tilde {v}_s)$ to be the ones that arise from the Krook collision operator (see § 2.4.2). We note that for this choice of collision operator, the constant
$C_s(\tilde {v}_s)$ to be the ones that arise from the Krook collision operator (see § 2.4.2). We note that for this choice of collision operator, the constant ![]() $\mathcal {C}_s$ defined by (2.34) is
$\mathcal {C}_s$ defined by (2.34) is ![]() $\mathcal {C}_s \approx 3/2$, and so the relationship (2.35) between the CE distribution functions’ pressure anisotropy
$\mathcal {C}_s \approx 3/2$, and so the relationship (2.35) between the CE distribution functions’ pressure anisotropy ![]() $\varDelta _s$ and the shear parameter
$\varDelta _s$ and the shear parameter ![]() $\epsilon _s$ becomes
$\epsilon _s$ becomes
We also observe that the CE shear terms have even parity with respect to the parallel velocity ![]() $v_{\|}$, and thus for any unstable mode with positive parallel wavenumber
$v_{\|}$, and thus for any unstable mode with positive parallel wavenumber ![]() $k_{\|} > 0$, there is a corresponding unstable mode with
$k_{\|} > 0$, there is a corresponding unstable mode with ![]() $k_{\|} < 0$. This conclusion has the consequence that the sign of
$k_{\|} < 0$. This conclusion has the consequence that the sign of ![]() $\epsilon _s$ (which is the same as the sign of
$\epsilon _s$ (which is the same as the sign of ![]() $(\hat {\boldsymbol {z}} \hat {\boldsymbol {z}} - \boldsymbol{\mathsf{I}}/3 ) \! \boldsymbol {:} \! \boldsymbol{\mathsf{W}}_s$, where
$(\hat {\boldsymbol {z}} \hat {\boldsymbol {z}} - \boldsymbol{\mathsf{I}}/3 ) \! \boldsymbol {:} \! \boldsymbol{\mathsf{W}}_s$, where ![]() $\boldsymbol{\mathsf{W}}_s$ is the rate-of-strain tensor of species
$\boldsymbol{\mathsf{W}}_s$ is the rate-of-strain tensor of species ![]() $s$ – see (2.12)) has a significant effect on possible types of CES microinstabilities. Thus, we must consider the cases
$s$ – see (2.12)) has a significant effect on possible types of CES microinstabilities. Thus, we must consider the cases ![]() $\epsilon _s > 0$ (positive pressure anisotropy,
$\epsilon _s > 0$ (positive pressure anisotropy, ![]() $\varDelta _s > 0$) and
$\varDelta _s > 0$) and ![]() $\epsilon _s < 0$ (negative pressure anisotropy,
$\epsilon _s < 0$ (negative pressure anisotropy, ![]() $\varDelta _s < 0$) separately. For easier comparison with previous work by other authors, we will sometimes substitute
$\varDelta _s < 0$) separately. For easier comparison with previous work by other authors, we will sometimes substitute ![]() $\epsilon _s =2 \varDelta _s/3$, and work in terms of
$\epsilon _s =2 \varDelta _s/3$, and work in terms of ![]() $\varDelta _s$.
$\varDelta _s$.
As with the discussion of CET microinstabilities in § 3, in the main text, we only present the main findings of our calculations: namely, the overview of the CES stability landscape (§ 4.2), and the analytical characterisation of CES microinstabilities with ![]() $\epsilon _s > 0$ (§ 4.3) and
$\epsilon _s > 0$ (§ 4.3) and ![]() $\epsilon _s < 0$ (§ 4.4). The methodology underlying the calculations of growth rates of CES microinstabilities is presented in Appendix K. Similarly to § 3, for the rest of this section, we assume without loss of generality that
$\epsilon _s < 0$ (§ 4.4). The methodology underlying the calculations of growth rates of CES microinstabilities is presented in Appendix K. Similarly to § 3, for the rest of this section, we assume without loss of generality that ![]() $k_{\|} > 0$ in all formulae.
$k_{\|} > 0$ in all formulae.
4.2. Stability
The stability of CE distribution functions of the form (4.1) is determined as a function of the parameters ![]() $\epsilon _i$,
$\epsilon _i$, ![]() $\epsilon _e$,
$\epsilon _e$, ![]() $d_e$,
$d_e$, ![]() $\beta _e$,
$\beta _e$, ![]() $\beta _i$ and the velocity scale length
$\beta _i$ and the velocity scale length ![]() $L_V = |(\hat {\boldsymbol {z}} \hat {\boldsymbol {z}} - \frac {1}{3}\boldsymbol{\mathsf{I}} ) \! \boldsymbol {:} \! \boldsymbol{\mathsf{W}}_i/V_i|^{-1}$ by assessing whether the maximum microinstability growth rate across all wavelengths smaller than
$L_V = |(\hat {\boldsymbol {z}} \hat {\boldsymbol {z}} - \frac {1}{3}\boldsymbol{\mathsf{I}} ) \! \boldsymbol {:} \! \boldsymbol{\mathsf{W}}_i/V_i|^{-1}$ by assessing whether the maximum microinstability growth rate across all wavelengths smaller than ![]() $\lambda _e$ and
$\lambda _e$ and ![]() $\lambda _i$ is negative or positive (see Appendix K for the methodology underpinning this calculation). As with the temperature-gradient-driven instabilities, we report the results of stability calculations that pertain to a temperature-equilibrated hydrogen plasma; that is, the particular case in which
$\lambda _i$ is negative or positive (see Appendix K for the methodology underpinning this calculation). As with the temperature-gradient-driven instabilities, we report the results of stability calculations that pertain to a temperature-equilibrated hydrogen plasma; that is, the particular case in which ![]() $\beta _i = \beta _e$ and
$\beta _i = \beta _e$ and ![]() $\epsilon _e = \mu _e^{1/2} \epsilon _i$ [where we recall that the characteristic magnitude of the CE electron velocity-shear term in such a plasma is smaller than the analogous CE ion-velocity-shear term by a factor of
$\epsilon _e = \mu _e^{1/2} \epsilon _i$ [where we recall that the characteristic magnitude of the CE electron velocity-shear term in such a plasma is smaller than the analogous CE ion-velocity-shear term by a factor of ![]() $\mu _e^{1/2} = (m_e/m_i)^{1/2}$]. Because
$\mu _e^{1/2} = (m_e/m_i)^{1/2}$]. Because ![]() $\epsilon _i$ can take both positive and negative values (see § 4.1), we do one stability calculation for each case; the results of these two calculations are shown in figures 8 and 9, respectively. The key characteristics of the stability of the CE distribution function (4.1) for ions and electrons can be shown using plots over a two-dimensional
$\epsilon _i$ can take both positive and negative values (see § 4.1), we do one stability calculation for each case; the results of these two calculations are shown in figures 8 and 9, respectively. The key characteristics of the stability of the CE distribution function (4.1) for ions and electrons can be shown using plots over a two-dimensional ![]() $(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space at fixed
$(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space at fixed ![]() $\beta _e$ and
$\beta _e$ and ![]() ${Ma}$ – we remind the reader that
${Ma}$ – we remind the reader that ![]() ${Ma} \, \lambda _e/L_V = |\epsilon _i|$, and that the Mach number
${Ma} \, \lambda _e/L_V = |\epsilon _i|$, and that the Mach number ![]() ${Ma}$ is assumed to satisfy
${Ma}$ is assumed to satisfy ![]() ${Ma} \lesssim 1$ – as opposed to the five-dimensional
${Ma} \lesssim 1$ – as opposed to the five-dimensional ![]() $(\epsilon _i,d_e,L_V,\beta _e,{Ma})$ parameter space that might naively be anticipated. This is because dimensional analysis again implies that
$(\epsilon _i,d_e,L_V,\beta _e,{Ma})$ parameter space that might naively be anticipated. This is because dimensional analysis again implies that ![]() $d_e$ and
$d_e$ and ![]() $L_{V}$ must appear in the stability boundary in the combination
$L_{V}$ must appear in the stability boundary in the combination ![]() $d_e/L_V$, and the two relevant stability thresholds are only functions of the product of
$d_e/L_V$, and the two relevant stability thresholds are only functions of the product of ![]() ${Ma}$ and
${Ma}$ and ![]() $d_e/L_V$ rather than their independent values.
$d_e/L_V$ rather than their independent values.

Figure 8. The CE-distribution-function stability map for CES microinstabilities driven by positive pressure anisotropy. Exploration of the stability of the ion and electron CE distribution functions (4.1) for different positive values of small parameters ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$ (viz. electron- or ion-pressure anisotropies), and the ratio of the electron inertial scale
$\epsilon _i$ (viz. electron- or ion-pressure anisotropies), and the ratio of the electron inertial scale ![]() $d_e$ to the velocity scale length
$d_e$ to the velocity scale length ![]() $L_V,$ in a temperature-equilibrated hydrogen plasma. In this plot, we chose
$L_V,$ in a temperature-equilibrated hydrogen plasma. In this plot, we chose ![]() $\epsilon _e = \mu _e^{1/2} \epsilon _i$, and then show
$\epsilon _e = \mu _e^{1/2} \epsilon _i$, and then show ![]() ${Ma} \, \lambda _e/L_V = |\epsilon _i|$ with equal logarithmic spacing in the range
${Ma} \, \lambda _e/L_V = |\epsilon _i|$ with equal logarithmic spacing in the range ![]() $[10^{-5},10^{0}]$;
$[10^{-5},10^{0}]$; ![]() $d_e/L_V$ is chosen with equal logarithmic spacing in the range
$d_e/L_V$ is chosen with equal logarithmic spacing in the range ![]() $[10^{-15},10^{0}]$. The total size of the grid is
$[10^{-15},10^{0}]$. The total size of the grid is ![]() $400^2$. For reasons of efficiency, we calculate growth rates on a
$400^2$. For reasons of efficiency, we calculate growth rates on a ![]() $40^2$ grid in wavenumber space with logarithmic spacing for both parallel and perpendicular wavenumbers. In this plot,
$40^2$ grid in wavenumber space with logarithmic spacing for both parallel and perpendicular wavenumbers. In this plot, ![]() $\beta _e = \beta _i = 10^4$, and
$\beta _e = \beta _i = 10^4$, and ![]() ${Ma} = 1$. (a) Stable (blue) and unstable (red) regions of
${Ma} = 1$. (a) Stable (blue) and unstable (red) regions of ![]() $(d_e/L_V,{Ma} \, \lambda _e/L_V)$ phase space. The theoretically anticipated collisional cutoffs (right – see (4.5)) and
$(d_e/L_V,{Ma} \, \lambda _e/L_V)$ phase space. The theoretically anticipated collisional cutoffs (right – see (4.5)) and ![]() $\beta$-stabilisation thresholds (horizontal dashed lines) for the CES mirror and parallel transverse instabilities, respectively, are also shown. (b) Maximum normalised microinstability growth rate (red) vs
$\beta$-stabilisation thresholds (horizontal dashed lines) for the CES mirror and parallel transverse instabilities, respectively, are also shown. (b) Maximum normalised microinstability growth rate (red) vs ![]() ${Ma} \, \lambda _e/L_V$ for a fixed electron inertial scale
${Ma} \, \lambda _e/L_V$ for a fixed electron inertial scale ![]() $d_e/L_V = 10^{-15}$, along with the maximum growth rate for the mirror instability (purple) in the limit
$d_e/L_V = 10^{-15}$, along with the maximum growth rate for the mirror instability (purple) in the limit ![]() ${Ma} \, \lambda _e \beta _e/L_V \gg 1$ (see (4.13)), and for the parallel transverse instability in the limit
${Ma} \, \lambda _e \beta _e/L_V \gg 1$ (see (4.13)), and for the parallel transverse instability in the limit ![]() ${Ma} \, \lambda _e \beta _e/L_V \gg \mu _e^{-1/2}$ (see (4.31), with
${Ma} \, \lambda _e \beta _e/L_V \gg \mu _e^{-1/2}$ (see (4.31), with ![]() $\theta = 0^{\circ }$). (c) Parallel wavenumber of the fastest-growing microinstability (red) vs
$\theta = 0^{\circ }$). (c) Parallel wavenumber of the fastest-growing microinstability (red) vs ![]() ${Ma} \, \lambda _e/L_V$ for a fixed electron inertial scale
${Ma} \, \lambda _e/L_V$ for a fixed electron inertial scale ![]() $d_e/L_V = 10^{-15}$, along with the same quantity analytically predicted for the mirror instability (purple) in the limit
$d_e/L_V = 10^{-15}$, along with the same quantity analytically predicted for the mirror instability (purple) in the limit ![]() ${Ma} \, \lambda _e \beta _e/L_V \gg 1$ (see (4.14a,b)), and for the parallel transverse instability (blue) in the limit
${Ma} \, \lambda _e \beta _e/L_V \gg 1$ (see (4.14a,b)), and for the parallel transverse instability (blue) in the limit ![]() ${Ma} \, \lambda _e \beta _e/L_V \gg \mu _e^{-1/2}$ (see (4.33a,b), with
${Ma} \, \lambda _e \beta _e/L_V \gg \mu _e^{-1/2}$ (see (4.33a,b), with ![]() $\theta = 0^{\circ }$). (d) Wavevector angle
$\theta = 0^{\circ }$). (d) Wavevector angle ![]() $\theta \equiv \tan ^{-1}{(k_{\|}/k_{\perp })}$ of the fastest-growing instability over the
$\theta \equiv \tan ^{-1}{(k_{\|}/k_{\perp })}$ of the fastest-growing instability over the ![]() $(d_e/L_V,{Ma} \, \lambda _e \beta _e/L_V)$ parameter space.
$(d_e/L_V,{Ma} \, \lambda _e \beta _e/L_V)$ parameter space.

Figure 9. The CE-distribution-function stability map for CES microinstabilities driven by negative pressure anisotropy. Same as figure 8, but for negative values of the small parameters ![]() $\epsilon _e$ and
$\epsilon _e$ and ![]() $\epsilon _i$. (a) Stable (blue) and unstable (red) regions of
$\epsilon _i$. (a) Stable (blue) and unstable (red) regions of ![]() $(d_e/L_V,{Ma} \, \lambda _e/L_V)$ phase space. The theoretically anticipated collisional cutoffs (right – see (4.5)) for the CES firehose and oblique transverse instabilities, respectively, and the
$(d_e/L_V,{Ma} \, \lambda _e/L_V)$ phase space. The theoretically anticipated collisional cutoffs (right – see (4.5)) for the CES firehose and oblique transverse instabilities, respectively, and the ![]() $\beta$-stabilisation thresholds (horizontal dashed lines) for the CES firehose, CES EST and whisper instabilities are also shown. (b) Maximum normalised microinstability growth rate (red) vs
$\beta$-stabilisation thresholds (horizontal dashed lines) for the CES firehose, CES EST and whisper instabilities are also shown. (b) Maximum normalised microinstability growth rate (red) vs ![]() ${Ma} \, \lambda _e/L_V$ for a fixed electron inertial scale
${Ma} \, \lambda _e/L_V$ for a fixed electron inertial scale ![]() $d_e/L_V = 10^{-15}$, along with analytically predicted maximum growth rate for the firehose instability (purple) (see (4.66)), for the EST instability (green) in the limit
$d_e/L_V = 10^{-15}$, along with analytically predicted maximum growth rate for the firehose instability (purple) (see (4.66)), for the EST instability (green) in the limit ![]() $\mu _e^{-1/2} \beta _e^{-5/7} \gg {Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2} \beta _e^{-1}$ (see (4.98)) for the whisper instability (yellow) in the limit
$\mu _e^{-1/2} \beta _e^{-5/7} \gg {Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2} \beta _e^{-1}$ (see (4.98)) for the whisper instability (yellow) in the limit ![]() $\mu _e^{-1/2} \beta _e^{-1/3} \gg {Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2} \beta _e^{-5/7}$ (see (4.110)), and for the oblique transverse instability (blue) in the limit
$\mu _e^{-1/2} \beta _e^{-1/3} \gg {Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2} \beta _e^{-5/7}$ (see (4.110)), and for the oblique transverse instability (blue) in the limit ![]() ${Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2} \beta _e^{-1}$ (see (4.101)). (c) Same as (b), but for the parallel wavenumber of the fastest-growing microinstability. The analytical predictions of this quantity for the firehose instability (purple) (see (4.67)), for the EST instability (green) (see (4.99b)) and for the whisper instability (yellow) (see (4.111b)), respectively, are also shown. (d) Same as (b), but for the perpendicular wavenumber of the fastest-growing microinstability. The analytical predictions of this quantity for the firehose instability (purple) (see (4.67)), for the EST instability (green) (see (4.99a)) and for the whisper instability (yellow) (see (4.111a)), are also shown.
${Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2} \beta _e^{-1}$ (see (4.101)). (c) Same as (b), but for the parallel wavenumber of the fastest-growing microinstability. The analytical predictions of this quantity for the firehose instability (purple) (see (4.67)), for the EST instability (green) (see (4.99b)) and for the whisper instability (yellow) (see (4.111b)), respectively, are also shown. (d) Same as (b), but for the perpendicular wavenumber of the fastest-growing microinstability. The analytical predictions of this quantity for the firehose instability (purple) (see (4.67)), for the EST instability (green) (see (4.99a)) and for the whisper instability (yellow) (see (4.111a)), are also shown.
The regions of stability presented in figure 8(a) for ![]() $\epsilon _i > 0$ (viz. for shear flows that drive positive pressure anisotropy) and in figure 9(a) for
$\epsilon _i > 0$ (viz. for shear flows that drive positive pressure anisotropy) and in figure 9(a) for ![]() $\epsilon _i < 0$ (viz. for shear flows driving negative pressure anisotropy), respectively, are broadly similar to the region of stability for CET microinstabilities described in § 3.2 (and shown in figure 2a), but with one crucial difference. Once again, for
$\epsilon _i < 0$ (viz. for shear flows driving negative pressure anisotropy), respectively, are broadly similar to the region of stability for CET microinstabilities described in § 3.2 (and shown in figure 2a), but with one crucial difference. Once again, for ![]() $d_e/L_V$ less than a critical value
$d_e/L_V$ less than a critical value ![]() $(d_e/L_V)_{c0}$, stability is independent of
$(d_e/L_V)_{c0}$, stability is independent of ![]() $d_e/L_V$, and there are no instabilities for
$d_e/L_V$, and there are no instabilities for ![]() ${Ma} \, \lambda _e \beta _e/L_V \ll 1$; for
${Ma} \, \lambda _e \beta _e/L_V \ll 1$; for ![]() $d_e/L_V \gtrsim (d_e/L_V)_{c0}$ and
$d_e/L_V \gtrsim (d_e/L_V)_{c0}$ and ![]() ${Ma} \, \lambda _e \beta _e/L_V > 1$, stability is guaranteed if (and only if)
${Ma} \, \lambda _e \beta _e/L_V > 1$, stability is guaranteed if (and only if) ![]() $d_e/L_V > (d_e/L_V)_{c}$ at fixed
$d_e/L_V > (d_e/L_V)_{c}$ at fixed ![]() ${Ma} \, \lambda _e/L_V$, where
${Ma} \, \lambda _e/L_V$, where ![]() $(d_e/L_V)_{c}$ is a monotonically increasing function of
$(d_e/L_V)_{c}$ is a monotonically increasing function of ![]() ${Ma} \, \lambda _e/L_V$. As before, these two bounding thresholds correspond to the
${Ma} \, \lambda _e/L_V$. As before, these two bounding thresholds correspond to the ![]() $\beta$-stabilisation conditions and collisional-stabilisation conditions, respectively, of CES microinstabilities. However, the dependence of
$\beta$-stabilisation conditions and collisional-stabilisation conditions, respectively, of CES microinstabilities. However, the dependence of ![]() $(d_e/L_V)_{c}$ on
$(d_e/L_V)_{c}$ on ![]() ${Ma} \, \lambda _e/L_V$ is more complicated than the analogous relationship between
${Ma} \, \lambda _e/L_V$ is more complicated than the analogous relationship between ![]() $(d_e/L_T)_{c}$ and
$(d_e/L_T)_{c}$ and ![]() ${Ma} \, \lambda _e/L_T$ that was presented in figure 2(a). Namely, if
${Ma} \, \lambda _e/L_T$ that was presented in figure 2(a). Namely, if ![]() ${Ma} \, \lambda _e/L_T \gtrsim \beta _e^{-1} \mu _e^{-1/2}$, then
${Ma} \, \lambda _e/L_T \gtrsim \beta _e^{-1} \mu _e^{-1/2}$, then ![]() $(d_e/L_V)_{c}$ suddenly shifts towards a larger value, with the subsequent (power-law) relationship between
$(d_e/L_V)_{c}$ suddenly shifts towards a larger value, with the subsequent (power-law) relationship between ![]() $(d_e/L_V)_{c}$ and
$(d_e/L_V)_{c}$ and ![]() ${Ma} \, \lambda _e/L_V$ being distinct from the analogous relationship when
${Ma} \, \lambda _e/L_V$ being distinct from the analogous relationship when ![]() ${Ma} \, \lambda _e/L_T \lesssim \beta _e^{-1} \mu _e^{-1/2}$. This behaviour is the result of a feature of the unstable region that is present for CES but not CET microinstabilities: different instabilities being dominant in different regions of the
${Ma} \, \lambda _e/L_T \lesssim \beta _e^{-1} \mu _e^{-1/2}$. This behaviour is the result of a feature of the unstable region that is present for CES but not CET microinstabilities: different instabilities being dominant in different regions of the ![]() $(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space. As we will see, this arises because CES microinstabilities on ion scales have less stringent
$(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space. As we will see, this arises because CES microinstabilities on ion scales have less stringent ![]() $\beta$-stabilisation thresholds than those on electron scales. Although their regions of stability are qualitatively similar, the types of microinstabilities that arise when
$\beta$-stabilisation thresholds than those on electron scales. Although their regions of stability are qualitatively similar, the types of microinstabilities that arise when ![]() $\epsilon _i > 0$ or
$\epsilon _i > 0$ or ![]() $\epsilon _i < 0$ are quite different, so we now discuss each case in turn.
$\epsilon _i < 0$ are quite different, so we now discuss each case in turn.
4.2.1. Positive pressure anisotropy
For ![]() $\epsilon _i > 0$ and
$\epsilon _i > 0$ and ![]() $0.5 \mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, the fastest-growing CES microinstability is the mirror instability: that is, a non-propagating, compressible slow mode on ion scales that is destabilised by positive ion pressure anisotropy. For
$0.5 \mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, the fastest-growing CES microinstability is the mirror instability: that is, a non-propagating, compressible slow mode on ion scales that is destabilised by positive ion pressure anisotropy. For ![]() ${Ma} \, \lambda _e \beta _e/L_V \gtrsim 0.5 \mu _e^{-1/2}$, a faster-growing CES microinstability emerges on electron-Larmor scales, driven by positive electron-pressure anisotropy: the whistler (electron-cyclotron) instability. For fixed
${Ma} \, \lambda _e \beta _e/L_V \gtrsim 0.5 \mu _e^{-1/2}$, a faster-growing CES microinstability emerges on electron-Larmor scales, driven by positive electron-pressure anisotropy: the whistler (electron-cyclotron) instability. For fixed ![]() $\beta _i$, the CES mirror instability can operate at smaller values of
$\beta _i$, the CES mirror instability can operate at smaller values of ![]() ${Ma} \, \lambda _e/L_V$ than the CES whistler instability, because the mirror-instability threshold
${Ma} \, \lambda _e/L_V$ than the CES whistler instability, because the mirror-instability threshold ![]() $\Delta _i \beta _i = 3 \,{Ma} \, \lambda _e \beta _i/2 L_V \geqslant 1$ (see § 4.3.1) is a less stringent condition on
$\Delta _i \beta _i = 3 \,{Ma} \, \lambda _e \beta _i/2 L_V \geqslant 1$ (see § 4.3.1) is a less stringent condition on ![]() ${Ma} \, \lambda _e/L_V$ for fixed
${Ma} \, \lambda _e/L_V$ for fixed ![]() $\beta _e$ than the threshold
$\beta _e$ than the threshold ![]() $\varDelta _e \beta _e = 3 \mu _e^{1/2}\, {Ma} \, \lambda _e \beta _i/2 L_V \gtrsim 0.5$ of the CES whistler instability (see § 4.3.2). On the other hand, once
$\varDelta _e \beta _e = 3 \mu _e^{1/2}\, {Ma} \, \lambda _e \beta _i/2 L_V \gtrsim 0.5$ of the CES whistler instability (see § 4.3.2). On the other hand, once ![]() ${Ma} \, \lambda _e \beta _e/L_V \gtrsim 0.5 \mu _e^{-1/2}$, the maximum growth rate of the CES mirror instability
${Ma} \, \lambda _e \beta _e/L_V \gtrsim 0.5 \mu _e^{-1/2}$, the maximum growth rate of the CES mirror instability ![]() $\gamma _{\rm mirr} \sim \varDelta _i \varOmega _i$ is much smaller than that of the CES whistler instability:
$\gamma _{\rm mirr} \sim \varDelta _i \varOmega _i$ is much smaller than that of the CES whistler instability: ![]() $\gamma _{{\rm whistler},S} \sim \varDelta _e \varOmega _e \sim \mu _e^{-1/2} \varDelta _i \varOmega _i \gg \varDelta _i \varOmega _i$. For
$\gamma _{{\rm whistler},S} \sim \varDelta _e \varOmega _e \sim \mu _e^{-1/2} \varDelta _i \varOmega _i \gg \varDelta _i \varOmega _i$. For ![]() ${Ma} \, \lambda _e \beta _e/L_V \gg \mu _e^{-1/2}$, in addition to unstable whistler modes, modes on sub-electron-Larmor scales are also destabilised: this is the parallel transverse instability, a microinstability that is essentially unmagnetised (
${Ma} \, \lambda _e \beta _e/L_V \gg \mu _e^{-1/2}$, in addition to unstable whistler modes, modes on sub-electron-Larmor scales are also destabilised: this is the parallel transverse instability, a microinstability that is essentially unmagnetised (![]() $k \rho _i \gg 1$) in character. When it can operate, the CES parallel transverse instability has a much larger growth rate than the unstable electron-Larmor-scale whistler waves,
$k \rho _i \gg 1$) in character. When it can operate, the CES parallel transverse instability has a much larger growth rate than the unstable electron-Larmor-scale whistler waves, ![]() $\gamma _{\rm trans} \sim \varDelta _e (\varDelta _e \beta )^{1/2} \varOmega _e \gg \gamma _{\rm whist} \sim \varDelta _e \varOmega _e$, so if
$\gamma _{\rm trans} \sim \varDelta _e (\varDelta _e \beta )^{1/2} \varOmega _e \gg \gamma _{\rm whist} \sim \varDelta _e \varOmega _e$, so if ![]() ${Ma} \, \lambda _e \beta _e/L_V \gg \mu _e^{-1/2}$, the transverse instability dominates.
${Ma} \, \lambda _e \beta _e/L_V \gg \mu _e^{-1/2}$, the transverse instability dominates.
Numerical evidence for the dominance of the CES mirror instability when ![]() $\mu _e^{-1/2} \gg {Ma} \, \lambda _e/L_V \gg 1$, and then the CES parallel transverse instability when
$\mu _e^{-1/2} \gg {Ma} \, \lambda _e/L_V \gg 1$, and then the CES parallel transverse instability when ![]() ${Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2}$, can be produced by isolating the maximum growth rate, the parallel wavenumber and the wavevector angle associated with peak growth for the unstable regions of the
${Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2}$, can be produced by isolating the maximum growth rate, the parallel wavenumber and the wavevector angle associated with peak growth for the unstable regions of the ![]() $(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space. Figure 8(b) shows that, for fixed
$(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space. Figure 8(b) shows that, for fixed ![]() $d_e/L_V$ and a range of
$d_e/L_V$ and a range of ![]() ${Ma} \, \lambda _e/L_V$, the peak microinstability growth rate is a reasonable match for that of the mirror instability (viz. (4.13)) for
${Ma} \, \lambda _e/L_V$, the peak microinstability growth rate is a reasonable match for that of the mirror instability (viz. (4.13)) for ![]() $0.5 \mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, and a good match for the parallel transverse instability (viz. (4.31)) for
$0.5 \mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, and a good match for the parallel transverse instability (viz. (4.31)) for ![]() ${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1}$. Figure 8(c) demonstrates that, for
${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1}$. Figure 8(c) demonstrates that, for ![]() $\mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, the (non-dimensionalised) parallel wavenumber
$\mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, the (non-dimensionalised) parallel wavenumber ![]() $(k_{\|} \rho _e)_{\rm peak}$ of peak growth satisfies
$(k_{\|} \rho _e)_{\rm peak}$ of peak growth satisfies ![]() $(k_{\|} \rho _e)_{\rm peak} \sim \mu _e^{-1/2}$, in agreement with the expected parallel wavenumber of the fastest-growing mirror modes (see (4.14a,b)). At
$(k_{\|} \rho _e)_{\rm peak} \sim \mu _e^{-1/2}$, in agreement with the expected parallel wavenumber of the fastest-growing mirror modes (see (4.14a,b)). At ![]() ${Ma} \, \lambda _e/L_V \sim \mu _e^{-1/2} \beta _e^{-1}$, there is a dramatic shift in
${Ma} \, \lambda _e/L_V \sim \mu _e^{-1/2} \beta _e^{-1}$, there is a dramatic shift in ![]() $(k_{\|} \rho _e)_{\rm peak}$ to a value
$(k_{\|} \rho _e)_{\rm peak}$ to a value ![]() $(k_{\|} \rho _e)_{\rm peak} \gtrsim 1$ that agrees with the expected parallel wavenumber of the parallel transverse instability (see (4.33a,b)). As for the peak-growth wavevector angle (figure 8d), for
$(k_{\|} \rho _e)_{\rm peak} \gtrsim 1$ that agrees with the expected parallel wavenumber of the parallel transverse instability (see (4.33a,b)). As for the peak-growth wavevector angle (figure 8d), for ![]() $\beta _e^{-1} \lesssim {Ma} \, \lambda _e/L_V \lesssim \mu _e^{-1/2} \beta _e^{-1}$, the dominant instability is oblique (as would be expected for the mirror instability), while for
$\beta _e^{-1} \lesssim {Ma} \, \lambda _e/L_V \lesssim \mu _e^{-1/2} \beta _e^{-1}$, the dominant instability is oblique (as would be expected for the mirror instability), while for ![]() ${Ma} \, \lambda _e/L_V \gtrsim 0.5 \mu _e^{-1/2} \beta _e^{-1}$, it is parallel (implying that the CES whistler/parallel transverse instability dominates). We conclude that the mirror instability is indeed dominant when
${Ma} \, \lambda _e/L_V \gtrsim 0.5 \mu _e^{-1/2} \beta _e^{-1}$, it is parallel (implying that the CES whistler/parallel transverse instability dominates). We conclude that the mirror instability is indeed dominant when ![]() $0.5 \mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, and the parallel transverse instability when
$0.5 \mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, and the parallel transverse instability when ![]() ${Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2} \beta _e^{-1}$.
${Ma} \, \lambda _e/L_V \gg \mu _e^{-1/2} \beta _e^{-1}$.
4.2.2. Negative pressure anisotropy
Now considering the case when ![]() $\epsilon _i < 0$, i.e. the case of negative pressure anisotropy, the only CES microinstability that operates when
$\epsilon _i < 0$, i.e. the case of negative pressure anisotropy, the only CES microinstability that operates when ![]() $\mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$ is the firehose instability: the destabilisation of Alfvén waves by ion-pressure anisotropies
$\mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$ is the firehose instability: the destabilisation of Alfvén waves by ion-pressure anisotropies ![]() $\varDelta _i \lesssim -1/\beta _i$.Footnote 3 If
$\varDelta _i \lesssim -1/\beta _i$.Footnote 3 If ![]() ${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1}$, several electron-scale CES microinstabilities arise, all of which tend to have larger growth rates than the firehose instability. The first of these to develop (at
${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1}$, several electron-scale CES microinstabilities arise, all of which tend to have larger growth rates than the firehose instability. The first of these to develop (at ![]() ${Ma} \, \lambda _e/L_V \sim \mu _e^{-1/2} \beta _e^{-1}$) is the oblique electron firehose instability: the destabilisation of oblique kinetic-Alfvén waves by negative electron-pressure anisotropy. For
${Ma} \, \lambda _e/L_V \sim \mu _e^{-1/2} \beta _e^{-1}$) is the oblique electron firehose instability: the destabilisation of oblique kinetic-Alfvén waves by negative electron-pressure anisotropy. For ![]() $\mu _e^{-1/2} \beta _e^{-1} \lesssim {Ma} \, \lambda _e/L_V \lesssim \mu _e^{-1/2} \beta _e^{-5/7}$, the EST instability begins to operate; this is a non-propagating quasi-perpendicular mode on electron-Larmor scales (
$\mu _e^{-1/2} \beta _e^{-1} \lesssim {Ma} \, \lambda _e/L_V \lesssim \mu _e^{-1/2} \beta _e^{-5/7}$, the EST instability begins to operate; this is a non-propagating quasi-perpendicular mode on electron-Larmor scales (![]() $k_{\perp } \rho _e \sim 1 \gg k_{\|} \rho _e$), which, while damped in a Maxwellian plasma, is unstable for sufficiently negative electron pressure anisotropies, and grows more rapidly than the oblique electron firehose instability. For
$k_{\perp } \rho _e \sim 1 \gg k_{\|} \rho _e$), which, while damped in a Maxwellian plasma, is unstable for sufficiently negative electron pressure anisotropies, and grows more rapidly than the oblique electron firehose instability. For ![]() $\mu _e^{-1/2} \beta _e^{-5/7} \lesssim {Ma} \, \lambda _e/L_V \lesssim \mu _e^{-1/2} \beta _e^{-1/3}$, the EST instability is surpassed by the whisper instability: the instability of a newly discovered propagating wave in a Maxwellian plasma (a whisper wave) whose perpendicular wavelength is on sub-electron-Larmor scales (
$\mu _e^{-1/2} \beta _e^{-5/7} \lesssim {Ma} \, \lambda _e/L_V \lesssim \mu _e^{-1/2} \beta _e^{-1/3}$, the EST instability is surpassed by the whisper instability: the instability of a newly discovered propagating wave in a Maxwellian plasma (a whisper wave) whose perpendicular wavelength is on sub-electron-Larmor scales (![]() $k_{\perp } \rho _e \gg 1$), but whose parallel wavelength is above the electron-Larmor scale (
$k_{\perp } \rho _e \gg 1$), but whose parallel wavelength is above the electron-Larmor scale (![]() $k_{\|} \rho _e < 1$). Finally, when
$k_{\|} \rho _e < 1$). Finally, when ![]() ${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1/3}$, the oblique transverse instability comes to predominate; unlike either the oblique electron firehose, the EST or whisper instabilities, it is unmagnetised in nature (like its parallel relative). Of these four instabilities, the oblique electron firehose and transverse instabilities have been identified previously (see references in §§ 4.4.7 and 4.4.9, respectively), but not the EST or whisper instabilities.
${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1/3}$, the oblique transverse instability comes to predominate; unlike either the oblique electron firehose, the EST or whisper instabilities, it is unmagnetised in nature (like its parallel relative). Of these four instabilities, the oblique electron firehose and transverse instabilities have been identified previously (see references in §§ 4.4.7 and 4.4.9, respectively), but not the EST or whisper instabilities.
We support these claims (in an analogous manner to the ![]() $\epsilon _i > 0$ case) by calculating the growth rate of the dominant microinstabilities for given points in the
$\epsilon _i > 0$ case) by calculating the growth rate of the dominant microinstabilities for given points in the ![]() $(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space. Figure 9(b) shows the maximum growth rate for a fixed value of
$(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space. Figure 9(b) shows the maximum growth rate for a fixed value of ![]() $d_e/L_V$. For
$d_e/L_V$. For ![]() $\mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, the peak growth rate follows the analytical prediction for the ion firehose instability,
$\mu _e^{-1/2} \beta _e^{-1} \gtrsim {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, the peak growth rate follows the analytical prediction for the ion firehose instability, ![]() $\gamma _{\rm fire} \sim |\varDelta _i|^{1/2} \varOmega _i/\sqrt {\log {1/|\varDelta _i|}}$, when
$\gamma _{\rm fire} \sim |\varDelta _i|^{1/2} \varOmega _i/\sqrt {\log {1/|\varDelta _i|}}$, when ![]() $\varDelta _i \ll -2/\beta _i$ (see (4.66)). For
$\varDelta _i \ll -2/\beta _i$ (see (4.66)). For ![]() ${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1}$, the peak growth rate becomes much greater than
${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1}$, the peak growth rate becomes much greater than ![]() $\gamma _{\rm fire}$; for
$\gamma _{\rm fire}$; for ![]() $\beta _e^{-5/7} \gtrsim \mu _e^{1/2} {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, it instead matches that of the EST instability,
$\beta _e^{-5/7} \gtrsim \mu _e^{1/2} {Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$, it instead matches that of the EST instability, ![]() $\gamma _{\mathrm {EST}} \sim |\varDelta _e| (|\varDelta _e| \beta _e)^{3/2} \varOmega _e/\sqrt {\log {|\varDelta _e| \beta _e}}$ (see (4.98)), where we remind the reader that
$\gamma _{\mathrm {EST}} \sim |\varDelta _e| (|\varDelta _e| \beta _e)^{3/2} \varOmega _e/\sqrt {\log {|\varDelta _e| \beta _e}}$ (see (4.98)), where we remind the reader that ![]() $|\varDelta _e| = 3 \mu _e^{1/2} {Ma} \, \lambda _e/2 L_V$. For
$|\varDelta _e| = 3 \mu _e^{1/2} {Ma} \, \lambda _e/2 L_V$. For ![]() $\mu _e^{1/2} {Ma} \, \lambda _e/L_V \gg \beta _e^{-5/7}$, the observed growth rate agrees with an analytical prediction for the whisper instability,
$\mu _e^{1/2} {Ma} \, \lambda _e/L_V \gg \beta _e^{-5/7}$, the observed growth rate agrees with an analytical prediction for the whisper instability, ![]() $\gamma _{\mathrm {whisp}} \sim |\varDelta _e|^{1/2} (|\varDelta _e| \beta _e)^{1/4} \varOmega _e/\sqrt {\log {|\varDelta _e| \beta _e}}$ (see (4.110)). Finally, because of the value of
$\gamma _{\mathrm {whisp}} \sim |\varDelta _e|^{1/2} (|\varDelta _e| \beta _e)^{1/4} \varOmega _e/\sqrt {\log {|\varDelta _e| \beta _e}}$ (see (4.110)). Finally, because of the value of ![]() $\beta _e$ chosen for this numerical example, the condition
$\beta _e$ chosen for this numerical example, the condition ![]() ${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1/3}$ under which the oblique transverse instability dominates is never met for
${Ma} \, \lambda _e/L_V \gtrsim \mu _e^{-1/2} \beta _e^{-1/3}$ under which the oblique transverse instability dominates is never met for ![]() ${Ma} \, \lambda _e/L_V \ll 1$, and thus the numerically measured growth rate of the dominant CES microinstability is larger than the transverse instability's peak growth rate
${Ma} \, \lambda _e/L_V \ll 1$, and thus the numerically measured growth rate of the dominant CES microinstability is larger than the transverse instability's peak growth rate ![]() $\gamma _{\rm trans} \sim |\varDelta _e| (|\varDelta _e| \beta _e)^{1/2} \varOmega _e$ (see (4.101)) for the entire range of
$\gamma _{\rm trans} \sim |\varDelta _e| (|\varDelta _e| \beta _e)^{1/2} \varOmega _e$ (see (4.101)) for the entire range of ![]() ${Ma} \, \lambda _e/L_V$ that we show in figure 9(b), (blue line).
${Ma} \, \lambda _e/L_V$ that we show in figure 9(b), (blue line).
A further confirmation that the most important microinstabilities are those that we have explicitly identified is obtained by calculating the parallel and perpendicular wavenumbers associated with the dominant microinstability. Figures 9(c) and 9(d) show that, for ![]() $\beta _e^{-1} \ll {Ma} \, \lambda _e/L_V \ll \mu _e^{-1/2} \beta _e^{-1}$,
$\beta _e^{-1} \ll {Ma} \, \lambda _e/L_V \ll \mu _e^{-1/2} \beta _e^{-1}$, ![]() $(k_\| \rho _e)_{\rm {peak}} \sim (k_\perp \rho _e)_{\rm {peak}} \sim \mu _e^{1/2}$. These values of
$(k_\| \rho _e)_{\rm {peak}} \sim (k_\perp \rho _e)_{\rm {peak}} \sim \mu _e^{1/2}$. These values of ![]() $(k_\| \rho _e)_{\rm {peak}}$ are consistent with the properties of the fastest-growing unstable firehose modes (see §§ 4.4.1 and 4.4.4), whose parallel wavenumber (approximately) satisfies
$(k_\| \rho _e)_{\rm {peak}}$ are consistent with the properties of the fastest-growing unstable firehose modes (see §§ 4.4.1 and 4.4.4), whose parallel wavenumber (approximately) satisfies ![]() $(k_\| \rho _i)_{\rm {peak}} \sim 1/\sqrt {\log {1/|\varDelta _i|}}$ when
$(k_\| \rho _i)_{\rm {peak}} \sim 1/\sqrt {\log {1/|\varDelta _i|}}$ when ![]() $\varDelta _i \ll -2/\beta _{i}$ (see (4.67)), and whose wavevector angle is
$\varDelta _i \ll -2/\beta _{i}$ (see (4.67)), and whose wavevector angle is ![]() $\theta _{\mathrm {peak}} \approx 39^{\rm {o}}$. At
$\theta _{\mathrm {peak}} \approx 39^{\rm {o}}$. At ![]() ${Ma} \, \lambda _e/L_V \sim \mu _e^{-1/2} \beta _e^{-1}$, the magnitudes of the parallel and perpendicular wavenumbers changes abruptly, to
${Ma} \, \lambda _e/L_V \sim \mu _e^{-1/2} \beta _e^{-1}$, the magnitudes of the parallel and perpendicular wavenumbers changes abruptly, to ![]() $(k_\| \rho _e)_{\rm {peak}} \sim (k_\perp \rho _e)_{\rm {peak}} \sim 1$; this is in line with expectations from the onset of the oblique electron firehose instability when
$(k_\| \rho _e)_{\rm {peak}} \sim (k_\perp \rho _e)_{\rm {peak}} \sim 1$; this is in line with expectations from the onset of the oblique electron firehose instability when ![]() $|\varDelta _e| \beta _e \sim 1$. For
$|\varDelta _e| \beta _e \sim 1$. For ![]() ${Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$ (
${Ma} \, \lambda _e/L_V \gg \beta _e^{-1}$ (![]() $|\varDelta _e| \beta _e \gg 1$), the parallel scale of the fastest-growing mode remains above electron-Larmor scales [
$|\varDelta _e| \beta _e \gg 1$), the parallel scale of the fastest-growing mode remains above electron-Larmor scales [![]() $(k_\| \rho _e)_{\rm {peak}} < 1$], while
$(k_\| \rho _e)_{\rm {peak}} < 1$], while ![]() $(k_\perp \rho _e)_{\rm {peak}}$ increases monotonically above unity. Both findings match theoretical expectations concerning the evolution of the parallel and perpendicular wavenumbers of the EST and whisper instabilities as functions of increasing
$(k_\perp \rho _e)_{\rm {peak}}$ increases monotonically above unity. Both findings match theoretical expectations concerning the evolution of the parallel and perpendicular wavenumbers of the EST and whisper instabilities as functions of increasing ![]() $|\varDelta _e| \beta _e$, and analytic formulae for these quantities are in reasonable agreement with the numerical results (see §§ 4.4.8 and 4.4.10).
$|\varDelta _e| \beta _e$, and analytic formulae for these quantities are in reasonable agreement with the numerical results (see §§ 4.4.8 and 4.4.10).
4.2.3. Collisional stabilisation
For both ![]() $\epsilon _i > 0$ and
$\epsilon _i > 0$ and ![]() $\epsilon _i < 0$, the shift in
$\epsilon _i < 0$, the shift in ![]() $(d_e/L_V)_{c}$ at
$(d_e/L_V)_{c}$ at ![]() ${Ma} \, \lambda _e/L_V \sim \mu _e^{-1/2} \beta _e^{-1}$ observed in figures 8(a) and 9(a) can be explained in terms of the ion-scale and electron-scale microinstabilities having distinct collisional-stabilisation conditions of the form (2.125) (viz.
${Ma} \, \lambda _e/L_V \sim \mu _e^{-1/2} \beta _e^{-1}$ observed in figures 8(a) and 9(a) can be explained in terms of the ion-scale and electron-scale microinstabilities having distinct collisional-stabilisation conditions of the form (2.125) (viz. ![]() $k \lambda _e \sim k \lambda _i \lesssim 1$), with the condition on the ion-scale instabilities being more restrictive. The wavenumbers
$k \lambda _e \sim k \lambda _i \lesssim 1$), with the condition on the ion-scale instabilities being more restrictive. The wavenumbers ![]() $k_{\rm mirr}$ and
$k_{\rm mirr}$ and ![]() $k_{\rm fire}$ at which maximal growth of the ion mirror and firehose instabilities occurs satisfy
$k_{\rm fire}$ at which maximal growth of the ion mirror and firehose instabilities occurs satisfy ![]() $k_{\rm mirr} \rho _i \sim 1$ and
$k_{\rm mirr} \rho _i \sim 1$ and ![]() $k_{\rm fire} \rho _i \lesssim 1$, respectively, for
$k_{\rm fire} \rho _i \lesssim 1$, respectively, for ![]() ${Ma} \, \lambda _e \beta _e/L_V \gg 1$, leading to the collisional-stabilisation condition
${Ma} \, \lambda _e \beta _e/L_V \gg 1$, leading to the collisional-stabilisation condition
For the electron-scale microinstabilities, the parallel and the oblique transverse instabilities have the largest (common) wavenumber of all such instabilities that operate when ![]() $\epsilon _i > 0$ and
$\epsilon _i > 0$ and ![]() $\epsilon _i < 0$, respectively, and so provide the most demanding collisional-stabilisation conditions. For both transverse instabilities, the wavenumber at which peak growth occurs satisfies
$\epsilon _i < 0$, respectively, and so provide the most demanding collisional-stabilisation conditions. For both transverse instabilities, the wavenumber at which peak growth occurs satisfies ![]() $k_{\rm trans} \rho _e \sim (\mu _e^{1/2} {Ma} \, \lambda _e \beta _e/L_V)^{1/2}$ (see (4.32)), which in turn can be rearranged to give the collisional-stabilisation condition
$k_{\rm trans} \rho _e \sim (\mu _e^{1/2} {Ma} \, \lambda _e \beta _e/L_V)^{1/2}$ (see (4.32)), which in turn can be rearranged to give the collisional-stabilisation condition
 \begin{equation} \frac{\lambda_e}{L_V} \lesssim {Ma}^{{-}1/3} \mu_e^{{-}1/6} \left(\frac{d_e}{L_V}\right)^{2/3} . \end{equation}
\begin{equation} \frac{\lambda_e}{L_V} \lesssim {Ma}^{{-}1/3} \mu_e^{{-}1/6} \left(\frac{d_e}{L_V}\right)^{2/3} . \end{equation}Bringing these results together, we find
 \begin{equation}
\left(\frac{d_e}{L_V}\right)_{c} = \left\{
\begin{array}{@{}ll} \mu_e^{1/2} \beta_e^{{-}1/2}
{\lambda_e}/{L_V} , & \beta_e^{{-}1} \ll {Ma} \,
{\lambda_e}/{L_V} < \mu_e^{{-}1/2} \beta_e^{{-}1}, \\
\mu_e^{1/4} {Ma}^{1/2}
\left({\lambda_e}/{L_V}\right)^{3/2}, & {Ma} \,
{\lambda_e}/{L_V} \gtrsim \mu_e^{{-}1/2} \beta_e^{{-}1},
\end{array} \right. \end{equation}
\begin{equation}
\left(\frac{d_e}{L_V}\right)_{c} = \left\{
\begin{array}{@{}ll} \mu_e^{1/2} \beta_e^{{-}1/2}
{\lambda_e}/{L_V} , & \beta_e^{{-}1} \ll {Ma} \,
{\lambda_e}/{L_V} < \mu_e^{{-}1/2} \beta_e^{{-}1}, \\
\mu_e^{1/4} {Ma}^{1/2}
\left({\lambda_e}/{L_V}\right)^{3/2}, & {Ma} \,
{\lambda_e}/{L_V} \gtrsim \mu_e^{{-}1/2} \beta_e^{{-}1},
\end{array} \right. \end{equation}
with ![]() $(d_e/L_V)_{c0} = \mu _e^{1/2} \beta _e^{-3/2}$. This matches asymptotically the numerical results shown in figures 8(a) and 9(a). These findings confirm that, once again, the relevant collisional-stabilisation condition for the microinstabilities with wavenumber
$(d_e/L_V)_{c0} = \mu _e^{1/2} \beta _e^{-3/2}$. This matches asymptotically the numerical results shown in figures 8(a) and 9(a). These findings confirm that, once again, the relevant collisional-stabilisation condition for the microinstabilities with wavenumber ![]() $k$ is
$k$ is ![]() $k \lambda _e = k \lambda _i\lesssim 1$ (viz. (2.125)), as opposed to the more restrictive conditions
$k \lambda _e = k \lambda _i\lesssim 1$ (viz. (2.125)), as opposed to the more restrictive conditions ![]() $\gamma \tau _i \lesssim 1$ and
$\gamma \tau _i \lesssim 1$ and ![]() $\gamma \tau _e \lesssim 1$ on the CES ion-scale and electron-scale instabilities, respectively. Similarly to the collisional-stabilisation condition on the CET whistler instability (see § 3.2), we note that the collisional-stabilisation condition on any of these microinstabilities can never actually be satisfied in a strongly magnetised plasma, because
$\gamma \tau _e \lesssim 1$ on the CES ion-scale and electron-scale instabilities, respectively. Similarly to the collisional-stabilisation condition on the CET whistler instability (see § 3.2), we note that the collisional-stabilisation condition on any of these microinstabilities can never actually be satisfied in a strongly magnetised plasma, because ![]() $k \lambda _i \gtrsim \lambda _i/\rho _i \gg 1$ for the ion-scale instabilities, and
$k \lambda _i \gtrsim \lambda _i/\rho _i \gg 1$ for the ion-scale instabilities, and ![]() $k \lambda _e \gtrsim \lambda _e/\rho _e \gg 1$ for the electron-scale instabilities.
$k \lambda _e \gtrsim \lambda _e/\rho _e \gg 1$ for the electron-scale instabilities.
4.2.4. Outline of the rest of this section
Further discussion about the properties and growth rates of CES microinstabilities with ![]() $\epsilon _s > 0$ (viz. those driven by positive pressure anisotropy) can be found in § 4.3, with the mirror, whistler and transverse instabilities discussed in §§ 4.3.1, 4.3.2 and 4.3.3, respectively. In addition to these, there is another instability (the electron mirror instability) that can be driven by positive pressure anisotropy of CE distribution functions that we note in passing: it consists in KAWs driven unstable by the CE electron-shear term, and to some extent by the ion-shear term (§ 4.3.4). The electron mirror instability does not appear to be the fastest-growing CES microinstability anywhere in the
$\epsilon _s > 0$ (viz. those driven by positive pressure anisotropy) can be found in § 4.3, with the mirror, whistler and transverse instabilities discussed in §§ 4.3.1, 4.3.2 and 4.3.3, respectively. In addition to these, there is another instability (the electron mirror instability) that can be driven by positive pressure anisotropy of CE distribution functions that we note in passing: it consists in KAWs driven unstable by the CE electron-shear term, and to some extent by the ion-shear term (§ 4.3.4). The electron mirror instability does not appear to be the fastest-growing CES microinstability anywhere in the ![]() $(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space; since the instability is subdominant to two other electron-scale instabilities (the whistler and transverse instabilities), this would seem to imply that the instability is comparatively less important.
$(d_e/L_V,{Ma} \, \lambda _e/L_V)$ parameter space; since the instability is subdominant to two other electron-scale instabilities (the whistler and transverse instabilities), this would seem to imply that the instability is comparatively less important.
CES microinstabilities with ![]() $\epsilon _s < 0$ (viz. those driven by negative pressure anisotropy) are explored in § 4.4. The firehose instability is overviewed in § 4.4.1, with then four subclasses of the instability (parallel, oblique, critical line and sub-ion-Larmor scale) considered in §§ 4.4.2, 4.4.3, 4.4.4 and 4.4.5. The oblique electron firehose instability is discussed in § 4.4.7, the EST instability in § 4.4.8, the oblique transverse instability in § 4.4.9 and the whisper instability in § 4.4.10. We identify two additional CES microinstabilities which are never the fastest-growing microinstability in any unstable region: the parallel electron firehose instability (§ 4.4.6), which (in spite of its name) has a different underlying physical mechanism than the oblique electron firehose, and the ordinary-mode instability (§ 4.4.11), which only operates at very high
$\epsilon _s < 0$ (viz. those driven by negative pressure anisotropy) are explored in § 4.4. The firehose instability is overviewed in § 4.4.1, with then four subclasses of the instability (parallel, oblique, critical line and sub-ion-Larmor scale) considered in §§ 4.4.2, 4.4.3, 4.4.4 and 4.4.5. The oblique electron firehose instability is discussed in § 4.4.7, the EST instability in § 4.4.8, the oblique transverse instability in § 4.4.9 and the whisper instability in § 4.4.10. We identify two additional CES microinstabilities which are never the fastest-growing microinstability in any unstable region: the parallel electron firehose instability (§ 4.4.6), which (in spite of its name) has a different underlying physical mechanism than the oblique electron firehose, and the ordinary-mode instability (§ 4.4.11), which only operates at very high ![]() $\beta _e$ (
$\beta _e$ (![]() $\beta _e \gtrsim |\varDelta _e|^{-3}$), and is only characteristically distinct from the oblique transverse instability in a regime in which it is slower growing.
$\beta _e \gtrsim |\varDelta _e|^{-3}$), and is only characteristically distinct from the oblique transverse instability in a regime in which it is slower growing.
Readers who do not wish to dwell on specific CES microinstabilities should proceed directly to § 5.
4.3. CES microinstability classification: positive pressure anisotropy ( $\epsilon _i > 0$)
$\epsilon _i > 0$)
4.3.1. Mirror instability
The CES mirror instability consists in the destabilisation of compressive slow modes by a sufficiently large positive ion-pressure anisotropy associated with the ion-shear term of the ion CE distribution function. In a high-![]() $\beta$ plasma with Maxwellian ion and electron distribution functions, the slow mode – which is one of the two plasma modes which exist at oblique wavevector angles
$\beta$ plasma with Maxwellian ion and electron distribution functions, the slow mode – which is one of the two plasma modes which exist at oblique wavevector angles ![]() $\theta \gtrsim \beta _i^{-1/4}$ (the other being the shear-Alfvén wave), and consists of a perturbation to the magnetic field's strength – is non-propagating, being subject to strong Barnes’ (equivalently, transit-time) damping (Barnes Reference Barnes1966). This damping is the result of Landau-resonant interactions between the slow mode and co-moving ions with
$\theta \gtrsim \beta _i^{-1/4}$ (the other being the shear-Alfvén wave), and consists of a perturbation to the magnetic field's strength – is non-propagating, being subject to strong Barnes’ (equivalently, transit-time) damping (Barnes Reference Barnes1966). This damping is the result of Landau-resonant interactions between the slow mode and co-moving ions with ![]() $v_{\|} = \omega /k_{\|}$; since, for a distribution function that decreases monotonically with
$v_{\|} = \omega /k_{\|}$; since, for a distribution function that decreases monotonically with ![]() $v_{\|} > 0$, there are more ions with
$v_{\|} > 0$, there are more ions with ![]() $v_{\|} < \omega /k_{\|}$ than with
$v_{\|} < \omega /k_{\|}$ than with ![]() $v_{\|} > \omega /k_{\|}$, there is a net transfer of free energy from the slow modes to the ions (as a particle acceleration process, this is sometimes called betatron acceleration). However, in a plasma with
$v_{\|} > \omega /k_{\|}$, there is a net transfer of free energy from the slow modes to the ions (as a particle acceleration process, this is sometimes called betatron acceleration). However, in a plasma with ![]() $\varDelta _i > 0$, there is an increase in the relative number of ions with large pitch angles in the troughs of the slow mode's magnetic-field strength perturbation, giving rise to excess perpendicular pressure. When
$\varDelta _i > 0$, there is an increase in the relative number of ions with large pitch angles in the troughs of the slow mode's magnetic-field strength perturbation, giving rise to excess perpendicular pressure. When ![]() $\varDelta _i > 1/\beta _i$, this excess pressure overbalances the magnetic pressure, leading to the mirror instability. In CE plasma with
$\varDelta _i > 1/\beta _i$, this excess pressure overbalances the magnetic pressure, leading to the mirror instability. In CE plasma with ![]() $0 < \varDelta _i \beta _i -1 \ll 1$, only quasi-perpendicular long-wavelength mirror modes (
$0 < \varDelta _i \beta _i -1 \ll 1$, only quasi-perpendicular long-wavelength mirror modes (![]() $k_{\|} \rho _i \ll k_{\perp } \rho _i \ll 1$) are destabilised; for larger values of
$k_{\|} \rho _i \ll k_{\perp } \rho _i \ll 1$) are destabilised; for larger values of ![]() $\varDelta _i$, a broad range of slow modes (including ion-Larmor-scale ones) become unstable. Chronologically, the earliest discussions of the mirror instability in pressure-anisotropic plasmas are due to Parker (Reference Parker1958) and Hasegawa (Reference Hasegawa1969). Southwood & Kivelson (Reference Southwood and Kivelson1993) provide a detailed and lucid discussion of the linear physics of the mirror instability (see also Kunz et al. Reference Kunz, Schekochihin, Chen, Abel and Cowley2015); various analytical (Pokhotelov et al. Reference Pokhotelov, Sagdeev, Balikhin, Onishchenko and Fedun2008; Rincon et al. Reference Rincon, Schekochihin and Cowley2015) and numerical (Hellinger et al. Reference Hellinger, Kuznetsov, Passot, Sulem and Trávníček2009; Kunz et al. Reference Kunz, Schekochihin and Stone2014; Riquelme et al. Reference Riquelme, Quataert and Verscharen2015; Melville et al. Reference Melville, Schekochihin and Kunz2016) studies investigating its nonlinear evolution have also been carried out.
$\varDelta _i$, a broad range of slow modes (including ion-Larmor-scale ones) become unstable. Chronologically, the earliest discussions of the mirror instability in pressure-anisotropic plasmas are due to Parker (Reference Parker1958) and Hasegawa (Reference Hasegawa1969). Southwood & Kivelson (Reference Southwood and Kivelson1993) provide a detailed and lucid discussion of the linear physics of the mirror instability (see also Kunz et al. Reference Kunz, Schekochihin, Chen, Abel and Cowley2015); various analytical (Pokhotelov et al. Reference Pokhotelov, Sagdeev, Balikhin, Onishchenko and Fedun2008; Rincon et al. Reference Rincon, Schekochihin and Cowley2015) and numerical (Hellinger et al. Reference Hellinger, Kuznetsov, Passot, Sulem and Trávníček2009; Kunz et al. Reference Kunz, Schekochihin and Stone2014; Riquelme et al. Reference Riquelme, Quataert and Verscharen2015; Melville et al. Reference Melville, Schekochihin and Kunz2016) studies investigating its nonlinear evolution have also been carried out.
The CES mirror instability can be characterised analytically – and simple expressions derived for the maximum growth rate and the wavevector at which that growth is attained – in the limit of marginal instability. First, we define the threshold parameter ![]() $\varGamma _i \equiv \beta _i \varDelta - 1$, where
$\varGamma _i \equiv \beta _i \varDelta - 1$, where ![]() $\varDelta \equiv \varDelta _i + \varDelta _e = (1+\mu _e^{1/2})\varDelta _i$, and assume that
$\varDelta \equiv \varDelta _i + \varDelta _e = (1+\mu _e^{1/2})\varDelta _i$, and assume that ![]() $\varGamma _i \ll 1$. It can then be shown (see Appendix K.3.2) that under the orderings
$\varGamma _i \ll 1$. It can then be shown (see Appendix K.3.2) that under the orderings
the mirror modes have a growth rate given by
 \begin{equation} \frac{\gamma}{\varOmega_i} = \frac{k_{\|} \rho_i}{\sqrt{\rm \pi} \beta_i} \left(\varGamma_i -\frac{3}{2} \frac{k_{\|}^2}{k_{\bot}^2}-\frac{3}{4} k_{\bot}^2 \rho_i^2 \right) . \end{equation}
\begin{equation} \frac{\gamma}{\varOmega_i} = \frac{k_{\|} \rho_i}{\sqrt{\rm \pi} \beta_i} \left(\varGamma_i -\frac{3}{2} \frac{k_{\|}^2}{k_{\bot}^2}-\frac{3}{4} k_{\bot}^2 \rho_i^2 \right) . \end{equation}
This is the same result as the growth rate of the mirror instability in a bi-Maxwellian plasma, with (the anticipated) threshold ![]() $\varGamma _i > 0$ (Hellinger Reference Hellinger2007). The peak growth rate
$\varGamma _i > 0$ (Hellinger Reference Hellinger2007). The peak growth rate ![]() $\gamma _{\mathrm {max}}$ is then given by
$\gamma _{\mathrm {max}}$ is then given by
achieved at the wavenumber
 \begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} = \frac{\varGamma_i}{3\sqrt{2}} , \quad (k_{\bot} \rho_i)_{\mathrm{peak}} = \frac{\varGamma_i^{1/2}}{\sqrt{3}} . \end{equation}
\begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} = \frac{\varGamma_i}{3\sqrt{2}} , \quad (k_{\bot} \rho_i)_{\mathrm{peak}} = \frac{\varGamma_i^{1/2}}{\sqrt{3}} . \end{equation}This recovers the results of Hellinger (Reference Hellinger2007).
Figure 10 illustrates the accuracy of the above predictions for ![]() $\gamma$ (and therefore
$\gamma$ (and therefore ![]() $\gamma _{\rm max}$),
$\gamma _{\rm max}$), ![]() $(k_{\|} \rho _i)_{\mathrm {peak}}$ and
$(k_{\|} \rho _i)_{\mathrm {peak}}$ and ![]() $(k_{\bot } \rho _i)_{\mathrm {peak}}$ by comparing them with the equivalent values obtained numerically using the general method outlined in Appendix K for a particular value of
$(k_{\bot } \rho _i)_{\mathrm {peak}}$ by comparing them with the equivalent values obtained numerically using the general method outlined in Appendix K for a particular value of ![]() $\varGamma _i \ll 1$. The wavenumber dependence of the numerically determined growth rate (see figure 10a) corroborates that, close to marginality, the unstable mirror modes are quasi-perpendicular; more quantitatively, the values of
$\varGamma _i \ll 1$. The wavenumber dependence of the numerically determined growth rate (see figure 10a) corroborates that, close to marginality, the unstable mirror modes are quasi-perpendicular; more quantitatively, the values of ![]() $k_{\|} \rho _i$ and
$k_{\|} \rho _i$ and ![]() $k_{\bot } \rho _i$ at which peak growth is obtained numerically match (4.9a,b). Furthermore, the growth rate (4.7) agrees well with the numerical result when plotted as a function of
$k_{\bot } \rho _i$ at which peak growth is obtained numerically match (4.9a,b). Furthermore, the growth rate (4.7) agrees well with the numerical result when plotted as a function of ![]() $k_{\|} \rho _i$ with fixed
$k_{\|} \rho _i$ with fixed ![]() $k_{\bot } \rho _i$, and also as a function of
$k_{\bot } \rho _i$, and also as a function of ![]() $k_{\bot } \rho _i$ with fixed
$k_{\bot } \rho _i$ with fixed ![]() $k_{\|} \rho _i$ (figure 10b).
$k_{\|} \rho _i$ (figure 10b).

Figure 10. Mirror instability at ![]() $\varGamma _i = \Delta \beta _i -1 \ll 1$. (a) Growth rates of unstable mirror modes resulting from the CE ion-shear term in the CE distribution function (4.1) for
$\varGamma _i = \Delta \beta _i -1 \ll 1$. (a) Growth rates of unstable mirror modes resulting from the CE ion-shear term in the CE distribution function (4.1) for ![]() $\varGamma _i = 0.04 \ll 1$ (
$\varGamma _i = 0.04 \ll 1$ (![]() $\Delta \beta _i = 1.04$). The growth rates of all modes are calculated using the approach outlined in Appendix K.3. The growth rates are calculated on a
$\Delta \beta _i = 1.04$). The growth rates of all modes are calculated using the approach outlined in Appendix K.3. The growth rates are calculated on a ![]() $400^2$ grid, with logarithmic spacing in both perpendicular and parallel directions between the minimum and maximum wavenumber magnitudes. The resulting growth rates, when normalised as
$400^2$ grid, with logarithmic spacing in both perpendicular and parallel directions between the minimum and maximum wavenumber magnitudes. The resulting growth rates, when normalised as ![]() $\gamma \beta _i/\varOmega _i$, are functions of the dimensionless quantity
$\gamma \beta _i/\varOmega _i$, are functions of the dimensionless quantity ![]() $\Delta \beta _i$. The dashed white lines indicate the analytical prediction (4.9a,b) for the wavenumber at which peak growth is achieved. (b) The mirror mode's growth rate (solid line) as a function of
$\Delta \beta _i$. The dashed white lines indicate the analytical prediction (4.9a,b) for the wavenumber at which peak growth is achieved. (b) The mirror mode's growth rate (solid line) as a function of ![]() $k_{\|} \rho _i$ with
$k_{\|} \rho _i$ with ![]() $k_{\bot } \rho _i = \varGamma _i^{1/2}/\sqrt {3}$ (top), and as a function of
$k_{\bot } \rho _i = \varGamma _i^{1/2}/\sqrt {3}$ (top), and as a function of ![]() $k_{\perp } \rho _i$ with
$k_{\perp } \rho _i$ with ![]() $k_{\|} \rho _i = \varGamma _i/3\sqrt {2}$ (bottom). The dashed lines show the analytical prediction (4.7) for these quantities.
$k_{\|} \rho _i = \varGamma _i/3\sqrt {2}$ (bottom). The dashed lines show the analytical prediction (4.7) for these quantities.
In contrast, for finite ![]() $\varGamma _i \gtrsim 1$, simple expressions for
$\varGamma _i \gtrsim 1$, simple expressions for ![]() $\gamma _{\rm max}$,
$\gamma _{\rm max}$, ![]() $(k_{\|} \rho _i)_{\mathrm {peak}}$ and
$(k_{\|} \rho _i)_{\mathrm {peak}}$ and ![]() $(k_{\bot } \rho _i)_{\mathrm {peak}}$ are challenging to derive analytically. Our numerical calculations indicate that, when
$(k_{\bot } \rho _i)_{\mathrm {peak}}$ are challenging to derive analytically. Our numerical calculations indicate that, when ![]() $\varGamma _i \sim 1$, a broad range of (purely growing) oblique modes becomes unstable, with maximum growth rate
$\varGamma _i \sim 1$, a broad range of (purely growing) oblique modes becomes unstable, with maximum growth rate ![]() $\gamma _{\rm max} \sim \varOmega _i/\beta _i \sim \Delta \varOmega _i$ attained when
$\gamma _{\rm max} \sim \varOmega _i/\beta _i \sim \Delta \varOmega _i$ attained when ![]() $k_{\|} \rho _i \lesssim k_{\perp } \rho _i \sim 1$ (figure 11a). Therefore, asymptotic expansions that treat
$k_{\|} \rho _i \lesssim k_{\perp } \rho _i \sim 1$ (figure 11a). Therefore, asymptotic expansions that treat ![]() $k_{\bot } \rho _i$ and
$k_{\bot } \rho _i$ and ![]() $k_{\|} \rho _i$ as small or large cannot be used to derive simplified expressions for the growth rate of the fastest-growing mirror modes. While the expressions (4.9a,b) for the wavenumber of peak growth derived in the case of near-marginality remain qualitatively correct, they are no longer quantitatively accurate; the same conclusion applies to the expression (4.7) for the growth rate when
$k_{\|} \rho _i$ as small or large cannot be used to derive simplified expressions for the growth rate of the fastest-growing mirror modes. While the expressions (4.9a,b) for the wavenumber of peak growth derived in the case of near-marginality remain qualitatively correct, they are no longer quantitatively accurate; the same conclusion applies to the expression (4.7) for the growth rate when ![]() $k_{\|} \rho _i \sim k_{\perp } \rho _i \sim 1$ (figure 11b). That being said, an expression similar to (4.7) can be derived (see Appendix K.3.2) for long-wavelength unstable mirror modes that satisfy the ordering
$k_{\|} \rho _i \sim k_{\perp } \rho _i \sim 1$ (figure 11b). That being said, an expression similar to (4.7) can be derived (see Appendix K.3.2) for long-wavelength unstable mirror modes that satisfy the ordering
This expression is
 \begin{equation} \frac{\gamma}{\varOmega_i} = \frac{k_{\|} \rho_i}{\sqrt{\rm \pi} \beta_i} \left(\varGamma_i -\frac{\varGamma_i + 3}{2} \frac{k_{\|}^2}{k_{\bot}^2}\right) . \end{equation}
\begin{equation} \frac{\gamma}{\varOmega_i} = \frac{k_{\|} \rho_i}{\sqrt{\rm \pi} \beta_i} \left(\varGamma_i -\frac{\varGamma_i + 3}{2} \frac{k_{\|}^2}{k_{\bot}^2}\right) . \end{equation}It implies that all such modes with
 \begin{equation} k_{\bot} > \left(\frac{3+\varGamma_i}{2 \varGamma_i}\right)^{1/2} k_{\|} ,\end{equation}
\begin{equation} k_{\bot} > \left(\frac{3+\varGamma_i}{2 \varGamma_i}\right)^{1/2} k_{\|} ,\end{equation}will be unstable, a prediction that is consistent with the unstable region observed in figure 11(a).

Figure 11. Mirror instability at ![]() $\varGamma _i = \Delta \beta _i -1 \sim 1$. (a) Growth rates of unstable mirror modes resulting from the CE ion-shear term in the CE distribution function (4.1) for
$\varGamma _i = \Delta \beta _i -1 \sim 1$. (a) Growth rates of unstable mirror modes resulting from the CE ion-shear term in the CE distribution function (4.1) for ![]() $\varGamma _i = 1$ (
$\varGamma _i = 1$ (![]() $\Delta \beta _i = 2$). The growth rates of all modes are calculated in the same way as in figure 10. The dashed white lines indicate the analytic prediction (4.9a,b) for the parallel/perpendicular wavenumber at which peak growth is achieved, while the dotted line indicates the analytical prediction (4.12) for the perpendicular wavenumber above which long-wavelength (
$\Delta \beta _i = 2$). The growth rates of all modes are calculated in the same way as in figure 10. The dashed white lines indicate the analytic prediction (4.9a,b) for the parallel/perpendicular wavenumber at which peak growth is achieved, while the dotted line indicates the analytical prediction (4.12) for the perpendicular wavenumber above which long-wavelength (![]() $k_{\|} \rho _i \lesssim k_{\perp } \rho _i \ll 1$) mirror modes become unstable. (b) The mirror mode's growth rate (solid line) as a function of
$k_{\|} \rho _i \lesssim k_{\perp } \rho _i \ll 1$) mirror modes become unstable. (b) The mirror mode's growth rate (solid line) as a function of ![]() $k_{\|} \rho _i$ with
$k_{\|} \rho _i$ with ![]() $k_{\bot } \rho _i = \varGamma _i^{1/2}/\sqrt {3}$ (top), and as a function of
$k_{\bot } \rho _i = \varGamma _i^{1/2}/\sqrt {3}$ (top), and as a function of ![]() $k_{\perp } \rho _i$ with
$k_{\perp } \rho _i$ with ![]() $k_{\|} \rho _i = \varGamma _i/3\sqrt {2}$ (bottom). The dashed lines show the analytical prediction (4.7) for this quantity.
$k_{\|} \rho _i = \varGamma _i/3\sqrt {2}$ (bottom). The dashed lines show the analytical prediction (4.7) for this quantity.
When ![]() $\varGamma _i \gg 1$, but
$\varGamma _i \gg 1$, but ![]() $\varGamma _i < (m_i/m_e)^{1/2}$, the region of
$\varGamma _i < (m_i/m_e)^{1/2}$, the region of ![]() $(k_{\|},k_{\bot })$ space in which mirror modes are unstable is qualitatively similar to the
$(k_{\|},k_{\bot })$ space in which mirror modes are unstable is qualitatively similar to the ![]() $\varGamma _i \sim 1$ case, albeit more extended (figure 12a). We find that in this limit, the maximum growth rate
$\varGamma _i \sim 1$ case, albeit more extended (figure 12a). We find that in this limit, the maximum growth rate ![]() $\gamma _{\mathrm {max}}$ becomes directly proportional to
$\gamma _{\mathrm {max}}$ becomes directly proportional to ![]() $\varDelta$ (see figure 12b), in contrast to the marginal case (4.7):
$\varDelta$ (see figure 12b), in contrast to the marginal case (4.7):
This growth is attained at parallel and perpendicular wavenumbers
which depend only weakly on ![]() $\Delta \beta _i$.
$\Delta \beta _i$.

Figure 12. Mirror instability at ![]() $\varGamma _i = \Delta \beta _i \gg 1$. (a) Growth rates of unstable mirror modes resulting from the CE ion-shear term in the CE distribution function (4.1) for
$\varGamma _i = \Delta \beta _i \gg 1$. (a) Growth rates of unstable mirror modes resulting from the CE ion-shear term in the CE distribution function (4.1) for ![]() $\varGamma _i = 29 \gg 1$ (
$\varGamma _i = 29 \gg 1$ (![]() $\Delta \beta _i = 30$). The growth rates of all modes are calculated in the same way as in figure 10. The dot-dashed white lines indicate the parallel/perpendicular wavenumbers (4.14a,b) at which peak growth is achieved, while the dotted line indicates the analytical prediction (4.12) for the perpendicular wavenumber above which long-wavelength (
$\Delta \beta _i = 30$). The growth rates of all modes are calculated in the same way as in figure 10. The dot-dashed white lines indicate the parallel/perpendicular wavenumbers (4.14a,b) at which peak growth is achieved, while the dotted line indicates the analytical prediction (4.12) for the perpendicular wavenumber above which long-wavelength (![]() $k_{\|} \rho _i \lesssim k_{\perp } \rho _i \ll 1$) mirror modes become unstable. (b) Normalised maximum positive growth rate
$k_{\|} \rho _i \lesssim k_{\perp } \rho _i \ll 1$) mirror modes become unstable. (b) Normalised maximum positive growth rate ![]() $\gamma _{\rm max}/\Delta \varOmega _i$ (solid red line) of the unstable mirror mode as a function of
$\gamma _{\rm max}/\Delta \varOmega _i$ (solid red line) of the unstable mirror mode as a function of ![]() $\Delta \beta _i$ along with the parallel (solid blue line) and perpendicular (solid yellow line) wavenumbers,
$\Delta \beta _i$ along with the parallel (solid blue line) and perpendicular (solid yellow line) wavenumbers, ![]() $(k_{\|} \rho _i)_{\mathrm {peak}}$ and
$(k_{\|} \rho _i)_{\mathrm {peak}}$ and ![]() $(k_{\perp } \rho _i)_{\mathrm {peak}}$ respectively, at which that growth is attained. The analytical prediction (4.7) of
$(k_{\perp } \rho _i)_{\mathrm {peak}}$ respectively, at which that growth is attained. The analytical prediction (4.7) of ![]() $\gamma _{\rm max}$ for marginally unstable modes, as well as the analogous predictions (4.9a,b) for
$\gamma _{\rm max}$ for marginally unstable modes, as well as the analogous predictions (4.9a,b) for ![]() $(k_{\|} \rho _i)_{\mathrm {peak}}$ and
$(k_{\|} \rho _i)_{\mathrm {peak}}$ and ![]() $(k_{\perp } \rho _i)_{\mathrm {peak}}$, are shown as dashed lines.
$(k_{\perp } \rho _i)_{\mathrm {peak}}$, are shown as dashed lines.
Some understanding of these results can be derived by considering the dispersion relation of mirror modes on sub-ion-Larmor scales. Adopting the ordering
while assuming that ![]() $\varDelta _i \beta _i \ll \mu _e^{-1/2}$, one finds (see Appendix K.3.2) that
$\varDelta _i \beta _i \ll \mu _e^{-1/2}$, one finds (see Appendix K.3.2) that
 \begin{equation} \frac{\gamma}{\varOmega_i} \approx \frac{k_\|}{k} \sqrt{\left(\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \frac{k_{\|}^2-k_{\bot}^2}{k^2} \right) \left(\varDelta_i \frac{k_{\|}^2}{k^2} - \frac{k^2 \rho_i^2}{\beta_i} \right)} . \end{equation}
\begin{equation} \frac{\gamma}{\varOmega_i} \approx \frac{k_\|}{k} \sqrt{\left(\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \frac{k_{\|}^2-k_{\bot}^2}{k^2} \right) \left(\varDelta_i \frac{k_{\|}^2}{k^2} - \frac{k^2 \rho_i^2}{\beta_i} \right)} . \end{equation}
This can be re-written in terms of the wavevector angle ![]() $\theta = \tan ^{-1}{(k_{\perp }/k_{\|})}$ as
$\theta = \tan ^{-1}{(k_{\perp }/k_{\|})}$ as
 \begin{equation} \frac{\gamma}{\varOmega_i} \approx \cos{\theta} \sqrt{\left[\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \left(\cos^2{\theta}-\sin^2{\theta}\right) \right] \left(\varDelta_i \cos^2{\theta} - \frac{k^2 \rho_i^2}{\beta_i} \right)} . \end{equation}
\begin{equation} \frac{\gamma}{\varOmega_i} \approx \cos{\theta} \sqrt{\left[\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \left(\cos^2{\theta}-\sin^2{\theta}\right) \right] \left(\varDelta_i \cos^2{\theta} - \frac{k^2 \rho_i^2}{\beta_i} \right)} . \end{equation}
Analysing this expression leads to three conclusions. First, for ![]() $\theta > 45^{\circ }$, there is an instability at all wavenumbers satisfying
$\theta > 45^{\circ }$, there is an instability at all wavenumbers satisfying ![]() $k \rho _i < (\varDelta _i \beta _i)^{1/2} \cos {\theta }$, explaining the expansion of the unstable region of
$k \rho _i < (\varDelta _i \beta _i)^{1/2} \cos {\theta }$, explaining the expansion of the unstable region of ![]() $(k_{\|},k_{\bot })$-space with increasing
$(k_{\|},k_{\bot })$-space with increasing ![]() $\varDelta _i \beta _i$. For
$\varDelta _i \beta _i$. For ![]() $\theta \leqslant 45^{\circ }$, growth only occurs over a more limited range of wavenumbers
$\theta \leqslant 45^{\circ }$, growth only occurs over a more limited range of wavenumbers ![]() $\sqrt {\cos ^2{\theta }-\sin ^2{\theta }} < k \rho _i/(\varDelta _i \beta _i)^{1/2} < \cos {\theta }$. Secondly, growth in this limit is maximised when
$\sqrt {\cos ^2{\theta }-\sin ^2{\theta }} < k \rho _i/(\varDelta _i \beta _i)^{1/2} < \cos {\theta }$. Secondly, growth in this limit is maximised when ![]() $k \rho _i \ll (\varDelta _i \beta _i)^{1/2}$, with the maximal growth rate
$k \rho _i \ll (\varDelta _i \beta _i)^{1/2}$, with the maximal growth rate
attained at ![]() $\cos {\theta } = 1/\sqrt {3}$ (
$\cos {\theta } = 1/\sqrt {3}$ (![]() $\theta \approx 55^{\circ }$). This expression for
$\theta \approx 55^{\circ }$). This expression for ![]() $\gamma _{\rm max}$ is (surprisingly) close to the numerically measured peak growth rate (4.13). For
$\gamma _{\rm max}$ is (surprisingly) close to the numerically measured peak growth rate (4.13). For ![]() $k \rho _i \sim (\varDelta _i \beta _i)^{1/2}$, the maximum growth rate is smaller than (4.18) by an order-unity factor. Finally, when
$k \rho _i \sim (\varDelta _i \beta _i)^{1/2}$, the maximum growth rate is smaller than (4.18) by an order-unity factor. Finally, when ![]() $k \rho _i \gg (\varDelta _i \beta _i)^{1/2}$, viz. in a wavenumber regime where there are no unstable mirror modes, (4.16) becomes imaginary, implying that the modes have a real frequency given by
$k \rho _i \gg (\varDelta _i \beta _i)^{1/2}$, viz. in a wavenumber regime where there are no unstable mirror modes, (4.16) becomes imaginary, implying that the modes have a real frequency given by
This is the dispersion relation of KAWs in a high-![]() $\beta$ plasma.Footnote 4 In short, at
$\beta$ plasma.Footnote 4 In short, at ![]() $\varDelta _i \beta _i \gg 1$, KAWs are also destabilised by positive ion-pressure anisotropy in addition to longer-wavelength mirror modes. We note that KAWs can also be destabilised by positive electron anisotropy, but the characteristic wavelength of such modes is preferentially comparable to electron-Larmor scales (see § 4.3.4).
$\varDelta _i \beta _i \gg 1$, KAWs are also destabilised by positive ion-pressure anisotropy in addition to longer-wavelength mirror modes. We note that KAWs can also be destabilised by positive electron anisotropy, but the characteristic wavelength of such modes is preferentially comparable to electron-Larmor scales (see § 4.3.4).
4.3.2. Whistler instability
The CES whistler instability arises when the free energy associated with positive electron-pressure anisotropy ![]() $\varDelta _e$ of the electron CE distribution function destabilises whistler waves, overwhelming both the electron-cyclotron damping (which is the dominant stabilisation mechanism for whistler waves with
$\varDelta _e$ of the electron CE distribution function destabilises whistler waves, overwhelming both the electron-cyclotron damping (which is the dominant stabilisation mechanism for whistler waves with ![]() $k_{\|} \rho _e \sim 1$) and the Landau damping due to the ion species (the dominant stabilisation mechanism for waves with
$k_{\|} \rho _e \sim 1$) and the Landau damping due to the ion species (the dominant stabilisation mechanism for waves with ![]() $k_{\|} \rho _e \ll 1$). In the special case of static ions, electron-cyclotron damping can be overcome by a positive electron-pressure anisotropy of any magnitude for whistler waves with sufficiently long wavelengths. Retaining mobile ions, the instability operates only if
$k_{\|} \rho _e \ll 1$). In the special case of static ions, electron-cyclotron damping can be overcome by a positive electron-pressure anisotropy of any magnitude for whistler waves with sufficiently long wavelengths. Retaining mobile ions, the instability operates only if ![]() $\varDelta _e$ exceeds a threshold of order
$\varDelta _e$ exceeds a threshold of order ![]() $(\varDelta _e)_{c} \sim \beta _e^{-1}$. When
$(\varDelta _e)_{c} \sim \beta _e^{-1}$. When ![]() $\varDelta _e > (\varDelta _e)_{c}$, gyroresonant interactions between electrons with
$\varDelta _e > (\varDelta _e)_{c}$, gyroresonant interactions between electrons with ![]() $v_{\|} = \pm \varOmega _e/k_{\|}$ and whistler waves allow for free energy to pass from the former to the latter, and so an increasingly broad spectrum of unstable parallel and oblique modes emerges on electron-Larmor scales. The analogue of this instability in a bi-Maxwellian plasma was found by Kennel & Petschek (Reference Kennel and Petschek1966), and it has since been studied numerically in moderately high-
$v_{\|} = \pm \varOmega _e/k_{\|}$ and whistler waves allow for free energy to pass from the former to the latter, and so an increasingly broad spectrum of unstable parallel and oblique modes emerges on electron-Larmor scales. The analogue of this instability in a bi-Maxwellian plasma was found by Kennel & Petschek (Reference Kennel and Petschek1966), and it has since been studied numerically in moderately high-![]() $\beta$ plasma (
$\beta$ plasma (![]() $\beta _e \sim 1\unicode{x2013}10$) by several authors (e.g. Gary & Wang Reference Gary and Wang1996; Guo et al. Reference Guo, Sironi and Narayan2014; Riquelme et al. Reference Riquelme, Quataert and Verscharen2016).
$\beta _e \sim 1\unicode{x2013}10$) by several authors (e.g. Gary & Wang Reference Gary and Wang1996; Guo et al. Reference Guo, Sironi and Narayan2014; Riquelme et al. Reference Riquelme, Quataert and Verscharen2016).
Similarly to the CET whistler instability, the simplest characterisation of the CES whistler instability is for unstable parallel whistler modes (viz. ![]() $k \approx k_{\|}$). Assuming that these modes satisfy the orderings
$k \approx k_{\|}$). Assuming that these modes satisfy the orderings
it can be shown (see Appendix K.3.3) that their real frequency ![]() $\varpi$ and growth rate
$\varpi$ and growth rate ![]() $\gamma$ satisfy
$\gamma$ satisfy
 $$\begin{align} \frac{\varpi \beta_e}{\varOmega_e} &={\pm} \varDelta_e \beta_e \pm \frac{k_{\|} \rho_e \left[\varDelta_e \beta_e \left(1+\mu_e^{1/2}\right)- k_\|^2 \rho_e^2\right] {\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)} }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 + {\rm \pi}\exp{\left(-{2}/{k_\|^2 \rho_e^2}\right)}}, \end{align}$$
$$\begin{align} \frac{\varpi \beta_e}{\varOmega_e} &={\pm} \varDelta_e \beta_e \pm \frac{k_{\|} \rho_e \left[\varDelta_e \beta_e \left(1+\mu_e^{1/2}\right)- k_\|^2 \rho_e^2\right] {\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)} }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 + {\rm \pi}\exp{\left(-{2}/{k_\|^2 \rho_e^2}\right)}}, \end{align}$$ $$\begin{align}\frac{\gamma \beta_e}{\varOmega_e} &= \frac{k_{\|} \rho_e \left[\exp{\left(-{1}/{k_\|^2 \rho_e^2}\right)}+\mu_e^{1/2}\right]\left(\varDelta_e \beta_e- k_\|^2 \rho_e^2\right) +\mu_e^{1/2} \varDelta_e \beta_e {\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)} }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2/\sqrt{\rm \pi} + \sqrt{\rm \pi} \exp{\left(-{2}/{k_\|^2 \rho_e^2}\right)}} , \end{align}$$
$$\begin{align}\frac{\gamma \beta_e}{\varOmega_e} &= \frac{k_{\|} \rho_e \left[\exp{\left(-{1}/{k_\|^2 \rho_e^2}\right)}+\mu_e^{1/2}\right]\left(\varDelta_e \beta_e- k_\|^2 \rho_e^2\right) +\mu_e^{1/2} \varDelta_e \beta_e {\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)} }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2/\sqrt{\rm \pi} + \sqrt{\rm \pi} \exp{\left(-{2}/{k_\|^2 \rho_e^2}\right)}} , \end{align}$$
where the terms proportional to ![]() $\mu _e^{1/2}$ are associated with the ion species.Footnote 5 In the limit
$\mu _e^{1/2}$ are associated with the ion species.Footnote 5 In the limit ![]() $\mu _e \rightarrow 0$, formally there is always instability provided
$\mu _e \rightarrow 0$, formally there is always instability provided ![]() $\varDelta _e \beta _e > 0$; however, for a hydrogen plasma (
$\varDelta _e \beta _e > 0$; however, for a hydrogen plasma (![]() $\mu _e \approx 1/1836$), it can be shown numerically that the numerator of (4.21b) only becomes positive (over a narrow interval of parallel wavenumbers around
$\mu _e \approx 1/1836$), it can be shown numerically that the numerator of (4.21b) only becomes positive (over a narrow interval of parallel wavenumbers around ![]() $k_{\|} \rho _e \approx 0.60$) for
$k_{\|} \rho _e \approx 0.60$) for ![]() $\varDelta _e \beta _e > 0.56$. The dispersion curves
$\varDelta _e \beta _e > 0.56$. The dispersion curves ![]() $\varpi (k_{\|})$ and
$\varpi (k_{\|})$ and ![]() $\gamma (k_{\|})$ of the unstable whistler waves in a hydrogen plasma for three different values of
$\gamma (k_{\|})$ of the unstable whistler waves in a hydrogen plasma for three different values of ![]() $\varDelta _e \beta _e$ that are above the necessary value for instability are shown in figure 13. When
$\varDelta _e \beta _e$ that are above the necessary value for instability are shown in figure 13. When ![]() $\varDelta _e \beta _e \gtrsim 1$, the growth rate is positive for a range
$\varDelta _e \beta _e \gtrsim 1$, the growth rate is positive for a range ![]() $\Delta k_{\|} \sim \rho _e^{-1}$ around
$\Delta k_{\|} \sim \rho _e^{-1}$ around ![]() $k_\| \rho _e \sim 1$, attaining a characteristic magnitude
$k_\| \rho _e \sim 1$, attaining a characteristic magnitude ![]() $\gamma \sim \varpi \sim \varOmega _e/\beta _e$.
$\gamma \sim \varpi \sim \varOmega _e/\beta _e$.

Figure 13. Parallel CES whistler instability. Dispersion curves of unstable whistler modes whose instability is driven by the electron-shear term in CE distribution function (4.1), for wavevectors that are co-parallel with the background magnetic field (viz. ![]() $\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The frequency (solid blue) and growth rate (solid red) of the modes are calculated using (4.21a) and (4.21b), respectively. The resulting frequencies and growth rates, when normalised as
$\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The frequency (solid blue) and growth rate (solid red) of the modes are calculated using (4.21a) and (4.21b), respectively. The resulting frequencies and growth rates, when normalised as ![]() $\gamma \beta _e/\varOmega _e$, are functions of the dimensionless quantity
$\gamma \beta _e/\varOmega _e$, are functions of the dimensionless quantity ![]() $\varDelta _e \beta _e$; we show the dispersion curves for three different values of
$\varDelta _e \beta _e$; we show the dispersion curves for three different values of ![]() $\varDelta _e \beta _e$. The approximations (4.22a) and (4.22b) for the frequency (dotted blue) and growth rate (dotted red) in the limit
$\varDelta _e \beta _e$. The approximations (4.22a) and (4.22b) for the frequency (dotted blue) and growth rate (dotted red) in the limit ![]() $k_{\|} \rho _e \ll 1$ are also plotted, as are the approximations (4.24a) and (4.24b) for the frequency (dashed blue) and growth rate (dashed red) in the limit
$k_{\|} \rho _e \ll 1$ are also plotted, as are the approximations (4.24a) and (4.24b) for the frequency (dashed blue) and growth rate (dashed red) in the limit ![]() $k_{\|} \rho _e \gg 1$.
$k_{\|} \rho _e \gg 1$.
As before, we characterise the growth rate for various values of ![]() $\varDelta _e \beta _e$ by taking subsidiary limits. First, for
$\varDelta _e \beta _e$ by taking subsidiary limits. First, for ![]() $\varDelta _e \beta _e \ll 1$, a necessary (though not always sufficient) condition for positive growth is
$\varDelta _e \beta _e \ll 1$, a necessary (though not always sufficient) condition for positive growth is ![]() $k_\| \rho _e < (\varDelta _e \beta _e)^{1/2} \ll 1$. We therefore expand (4.21) in
$k_\| \rho _e < (\varDelta _e \beta _e)^{1/2} \ll 1$. We therefore expand (4.21) in ![]() $k_\| \rho _e \sim (\varDelta _e \beta _e)^{1/2} \ll 1$, finding that
$k_\| \rho _e \sim (\varDelta _e \beta _e)^{1/2} \ll 1$, finding that
 $$\begin{align}\gamma &\approx \frac{\sqrt{\rm \pi}}{k_\| \rho_e} \left\{\exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} \left(\varDelta_e - \frac{k_\|^2 \rho_e^2}{\beta_e}\right) -\mu_e^{1/2} \frac{k_\|^2 \rho_e^2}{\beta_e} \right\} \varOmega_e . \end{align}$$
$$\begin{align}\gamma &\approx \frac{\sqrt{\rm \pi}}{k_\| \rho_e} \left\{\exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} \left(\varDelta_e - \frac{k_\|^2 \rho_e^2}{\beta_e}\right) -\mu_e^{1/2} \frac{k_\|^2 \rho_e^2}{\beta_e} \right\} \varOmega_e . \end{align}$$
Similarly to what we showed in § 3.3.1 for the CET whistler instability, we have once again found unstable whistler waves. For comparison's sake, the approximate expressions (4.22) are plotted in figure 13 in addition to their exact analogues (4.21); it is clear that there is reasonable agreement for a moderately small value of ![]() $\varDelta _e \beta _e$, but that the approximations become less accurate for
$\varDelta _e \beta _e$, but that the approximations become less accurate for ![]() $k_\| \rho _e \gtrsim 0.5$ and
$k_\| \rho _e \gtrsim 0.5$ and ![]() $\varDelta _e \beta _e > 1$.
$\varDelta _e \beta _e > 1$.
In the limit ![]() $\mu _e \rightarrow 0$, the expression (4.22b) for the growth rate is very similar to that of the whistler (electron-cyclotron) instability in a plasma with a bi-Maxwellian distribution and positive electron-pressure anisotropy (Davidson Reference Davidson1983). In this case, whistler modes with
$\mu _e \rightarrow 0$, the expression (4.22b) for the growth rate is very similar to that of the whistler (electron-cyclotron) instability in a plasma with a bi-Maxwellian distribution and positive electron-pressure anisotropy (Davidson Reference Davidson1983). In this case, whistler modes with ![]() $k_\| \rho _e < (\varDelta _e \beta _e)^{1/2}$ are always unstable, although the growth rate of such modes is exponentially small in
$k_\| \rho _e < (\varDelta _e \beta _e)^{1/2}$ are always unstable, although the growth rate of such modes is exponentially small in ![]() $\varDelta _e \beta _e \ll 1$ as compared with the frequency (4.22a), and so
$\varDelta _e \beta _e \ll 1$ as compared with the frequency (4.22a), and so ![]() $\gamma \ll \varpi \sim \varOmega _e/\beta _e$. By contrast, with small but finite
$\gamma \ll \varpi \sim \varOmega _e/\beta _e$. By contrast, with small but finite ![]() $\mu _e = m_e/m_i$, it can be shown analytically that, for (4.22b) to be positive,
$\mu _e = m_e/m_i$, it can be shown analytically that, for (4.22b) to be positive, ![]() $\varDelta _e > (\varDelta _e)_{\rm c}$, where
$\varDelta _e > (\varDelta _e)_{\rm c}$, where
 \begin{align} (\varDelta_e)_{c} & = \frac{1}{\beta_e W_{\rm Lam}\left[\mu_e^{{-}1/2}\exp{({-}1)}\right]}\nonumber\\ & \approx \frac{1}{\beta_e} \frac{1}{\log{(\mu_e^{{-}1/2})}-1-\log{[\log{(\mu_e^{{-}1/2})}-1}]} . \end{align}
\begin{align} (\varDelta_e)_{c} & = \frac{1}{\beta_e W_{\rm Lam}\left[\mu_e^{{-}1/2}\exp{({-}1)}\right]}\nonumber\\ & \approx \frac{1}{\beta_e} \frac{1}{\log{(\mu_e^{{-}1/2})}-1-\log{[\log{(\mu_e^{{-}1/2})}-1}]} . \end{align}
Here, ![]() $W_{\rm Lam}(x)$ denotes the Lambert W function (Corless et al. Reference Corless, Gonnet, Hare, Jeffrey and Knuth1996). Unstable modes first develop around
$W_{\rm Lam}(x)$ denotes the Lambert W function (Corless et al. Reference Corless, Gonnet, Hare, Jeffrey and Knuth1996). Unstable modes first develop around ![]() $(k_{\|} \rho _e)_c = (\varDelta _e)_{c}^{1/2} /[(\varDelta _e)_{c}+1/\beta _e]^{1/2}$. In a hydrogen plasma, this gives
$(k_{\|} \rho _e)_c = (\varDelta _e)_{c}^{1/2} /[(\varDelta _e)_{c}+1/\beta _e]^{1/2}$. In a hydrogen plasma, this gives ![]() $(\varDelta _e)_{c} \approx 0.49/\beta _e$ and
$(\varDelta _e)_{c} \approx 0.49/\beta _e$ and ![]() $(k_{\|} \rho _e)_c \approx 0.57$, which are similar to the instability threshold and wavenumber, respectively, determined numerically if
$(k_{\|} \rho _e)_c \approx 0.57$, which are similar to the instability threshold and wavenumber, respectively, determined numerically if ![]() $\gamma$ is computed for arbitrary values of
$\gamma$ is computed for arbitrary values of ![]() $k_{\|} \rho _e$; the small discrepancy is due to the finite value of
$k_{\|} \rho _e$; the small discrepancy is due to the finite value of ![]() $k_{\|} \rho _e$ at which instability first emerges. Formally,
$k_{\|} \rho _e$ at which instability first emerges. Formally, ![]() $(\varDelta _e)_{c} \rightarrow 0$ as
$(\varDelta _e)_{c} \rightarrow 0$ as ![]() $\mu _e \rightarrow 0$, but the limit converges only logarithmically in
$\mu _e \rightarrow 0$, but the limit converges only logarithmically in ![]() $\mu _e$, suggesting that in an actual plasma, the CES whistler instability will generically have a threshold at a finite value of
$\mu _e$, suggesting that in an actual plasma, the CES whistler instability will generically have a threshold at a finite value of ![]() $\varDelta _e \beta _e$.
$\varDelta _e \beta _e$.
Let us now turn to the opposite subsidiary limit ![]() $\varDelta _e \beta _e \gg 1$. We find from (4.21b) that maximal growth occurs at
$\varDelta _e \beta _e \gg 1$. We find from (4.21b) that maximal growth occurs at ![]() $k_\| \rho _e \sim (\varDelta _e \beta )^{1/2} \gg 1$
$k_\| \rho _e \sim (\varDelta _e \beta )^{1/2} \gg 1$
 $$\begin{align} \varpi &\approx \frac{1}{\rm \pi}\left[\varDelta_e \left({\rm \pi}-2\right)+ \frac{k_\|^2 \rho_e^2}{\beta_e}\right] \varOmega_e , \end{align}$$
$$\begin{align} \varpi &\approx \frac{1}{\rm \pi}\left[\varDelta_e \left({\rm \pi}-2\right)+ \frac{k_\|^2 \rho_e^2}{\beta_e}\right] \varOmega_e , \end{align}$$ $$\begin{align}\gamma &\approx \frac{k_\| \rho_e}{\sqrt{\rm \pi}} \left(\varDelta_e - \frac{k_\|^2 \rho_e^2}{\beta_e}\right) \varOmega_e . \end{align}$$
$$\begin{align}\gamma &\approx \frac{k_\| \rho_e}{\sqrt{\rm \pi}} \left(\varDelta_e - \frac{k_\|^2 \rho_e^2}{\beta_e}\right) \varOmega_e . \end{align}$$
Alongside ![]() $k_\| \rho _e \ll 1$ approximations, these approximations are plotted in figure 13, and agree well with the numerical results for
$k_\| \rho _e \ll 1$ approximations, these approximations are plotted in figure 13, and agree well with the numerical results for ![]() $\varDelta _e \beta _e \gtrsim 3$ and
$\varDelta _e \beta _e \gtrsim 3$ and ![]() $k_\| \rho _e \gtrsim 2$. The maximum growth rate
$k_\| \rho _e \gtrsim 2$. The maximum growth rate
is attained at the parallel wavenumber
 \begin{equation} (k_\|
\rho_e)_{\mathrm{peak}} = \left(\frac{\varDelta_e \beta_e}{3}\right)^{1/2}.
\end{equation}
\begin{equation} (k_\|
\rho_e)_{\mathrm{peak}} = \left(\frac{\varDelta_e \beta_e}{3}\right)^{1/2}.
\end{equation}A notable feature of the CES whistler instability in this subsidiary limit is that the fastest-growing modes are on sub-electron-Larmor scales; thus, such modes are arguably better conceptualised not as whistler modes, but as unstable, unmagnetised plasma modes (see § 4.3.3).
Similarly to the CET whistler instability, analytical expressions for the frequency and growth rate of unstable modes that have an oblique wavevector angle are much less simple that the analogous expressions for parallel whistler modes. It can be shown (see Appendix K.2) that the complex frequency of such modes is given by
where the functions ![]() $A_{S} = A_{S}(k_{\|} \rho _e,k_{\perp } \rho _e,\varDelta _e \beta _e)$,
$A_{S} = A_{S}(k_{\|} \rho _e,k_{\perp } \rho _e,\varDelta _e \beta _e)$, ![]() $B_{S} = B_{S}(k_{\|} \rho _e,k_{\perp } \rho _e,\varDelta _e \beta _e)$ and
$B_{S} = B_{S}(k_{\|} \rho _e,k_{\perp } \rho _e,\varDelta _e \beta _e)$ and ![]() $C_{S} = C_{S}(k_{\|} \rho _e,k_{\perp } \rho _e,\varDelta _e \beta _e)$ are composed of the sums and products of special mathematical functions. When
$C_{S} = C_{S}(k_{\|} \rho _e,k_{\perp } \rho _e,\varDelta _e \beta _e)$ are composed of the sums and products of special mathematical functions. When ![]() $\varDelta _e \beta _e \sim 1$, (4.27) implies that if there is an instability, its growth rate will be of order
$\varDelta _e \beta _e \sim 1$, (4.27) implies that if there is an instability, its growth rate will be of order ![]() $\gamma \sim \varOmega _e/\beta _e$ at
$\gamma \sim \varOmega _e/\beta _e$ at ![]() $k_{\|} \rho _e, k_{\perp } \rho _e \sim 1$.
$k_{\|} \rho _e, k_{\perp } \rho _e \sim 1$.
To confirm this expectation, in figure 14 we plot the maximum growth rate (obtained numerically) of oblique modes across the ![]() $(k_{\|},k_{\perp })$-plane for two of the values of
$(k_{\|},k_{\perp })$-plane for two of the values of ![]() $\varDelta _e \beta _e$ used in figure 13. For
$\varDelta _e \beta _e$ used in figure 13. For ![]() $\varDelta _e \beta _e$ not far beyond the threshold of the CES whistler instability (figure 14a), the unstable modes are quasi-parallel and have growth rates
$\varDelta _e \beta _e$ not far beyond the threshold of the CES whistler instability (figure 14a), the unstable modes are quasi-parallel and have growth rates ![]() $\gamma \ll \varOmega _e/\beta _e$ (cf. figure 13a). For
$\gamma \ll \varOmega _e/\beta _e$ (cf. figure 13a). For ![]() $\varDelta _e \beta _e \gtrsim 1$, a broader spectrum of wavenumbers becomes unstable (figure 14b). The parallel mode remains the fastest growing in this case; however, oblique modes with
$\varDelta _e \beta _e \gtrsim 1$, a broader spectrum of wavenumbers becomes unstable (figure 14b). The parallel mode remains the fastest growing in this case; however, oblique modes with ![]() $k_{\perp } \lesssim k_{\|}/2$ also have growth rates of comparable magnitude: e.g. the fastest-growing mode with wavevector angle
$k_{\perp } \lesssim k_{\|}/2$ also have growth rates of comparable magnitude: e.g. the fastest-growing mode with wavevector angle ![]() $\theta = 10^{\circ }$ has
$\theta = 10^{\circ }$ has ![]() $\gamma _{\rm max}/\gamma _{\rm max}(k_{\perp } = 0) \approx 0.93$, and for a wavevector angle
$\gamma _{\rm max}/\gamma _{\rm max}(k_{\perp } = 0) \approx 0.93$, and for a wavevector angle ![]() $\theta = 10^{\circ }$,
$\theta = 10^{\circ }$, ![]() $\gamma _{\rm max}/\gamma _{\rm max}(k_{\perp } = 0) \approx 0.76$. For more oblique angles, the growth rate is reduced significantly: e.g. for
$\gamma _{\rm max}/\gamma _{\rm max}(k_{\perp } = 0) \approx 0.76$. For more oblique angles, the growth rate is reduced significantly: e.g. for ![]() $\theta = 30^{\circ }$,
$\theta = 30^{\circ }$, ![]() $\gamma _{\rm max}/\gamma _{\rm max}(k_{\perp } = 0) \approx 0.22$. Thus, we conclude that a spectrum of oblique modes in addition to parallel ones is indeed destabilised, with
$\gamma _{\rm max}/\gamma _{\rm max}(k_{\perp } = 0) \approx 0.22$. Thus, we conclude that a spectrum of oblique modes in addition to parallel ones is indeed destabilised, with ![]() $\gamma \sim \varOmega _e/\beta _e \lesssim \gamma (k_{\perp } = 0)$.
$\gamma \sim \varOmega _e/\beta _e \lesssim \gamma (k_{\perp } = 0)$.

Figure 14. Oblique unstable modes at ![]() $\varDelta _e \beta _e \sim 1$: (a)
$\varDelta _e \beta _e \sim 1$: (a) ![]() $\varDelta _e \beta _e = 0.75$; (b)
$\varDelta _e \beta _e = 0.75$; (b) ![]() $\varDelta _e \beta _e = 3$. Maximum positive growth rates of linear perturbations resulting from CE ion- and electron-shear terms in the CE distribution function (4.1) for
$\varDelta _e \beta _e = 3$. Maximum positive growth rates of linear perturbations resulting from CE ion- and electron-shear terms in the CE distribution function (4.1) for ![]() $\varDelta _e \beta _e \sim 1$. Here, a temperature-equilibrated hydrogen plasma is considered, viz.
$\varDelta _e \beta _e \sim 1$. Here, a temperature-equilibrated hydrogen plasma is considered, viz. ![]() $\varDelta _e = \mu _e^{1/2} \varDelta _i$, and
$\varDelta _e = \mu _e^{1/2} \varDelta _i$, and ![]() $\beta _i = \beta _e$. The growth rates of all modes are calculated using the approach outlined in Appendix K.3. The growth rates are calculated on a
$\beta _i = \beta _e$. The growth rates of all modes are calculated using the approach outlined in Appendix K.3. The growth rates are calculated on a ![]() $400^2$ grid, with logarithmic spacing between wavenumbers in both perpendicular and parallel directions. The resulting growth rates, when normalised as
$400^2$ grid, with logarithmic spacing between wavenumbers in both perpendicular and parallel directions. The resulting growth rates, when normalised as ![]() $\gamma \beta _e/\varOmega _e$, are functions of
$\gamma \beta _e/\varOmega _e$, are functions of ![]() $\varDelta _e \beta _e$, or, equivalently,
$\varDelta _e \beta _e$, or, equivalently, ![]() $\epsilon _e \beta _e$. The vertical dashed lines indicate
$\epsilon _e \beta _e$. The vertical dashed lines indicate ![]() $k_{\|} \rho _i = 1$ and
$k_{\|} \rho _i = 1$ and ![]() $k_{\|} \rho _e = 1$, respectively, while the horizontal ones indicate
$k_{\|} \rho _e = 1$, respectively, while the horizontal ones indicate ![]() $k_{\perp } \rho _i = 1$ and
$k_{\perp } \rho _i = 1$ and ![]() $k_{\perp } \rho _e = 1$.
$k_{\perp } \rho _e = 1$.
We note that, in addition to oblique CES whistler modes, whose characteristic wavenumber domain is ![]() $k_{\perp } \rho _e \lesssim k_{\|} \rho _i \sim 1$, we observe two other unstable modes in figure 14(a) with different characteristic values of
$k_{\perp } \rho _e \lesssim k_{\|} \rho _i \sim 1$, we observe two other unstable modes in figure 14(a) with different characteristic values of ![]() $k_{\|}$ and
$k_{\|}$ and ![]() $k_{\perp }$. The first of these, which exists on ion scales, is the CES mirror instability, which we already discussed in § 4.3.1. The second is the CES electron mirror instability – we shall consider this instability in § 4.3.4.
$k_{\perp }$. The first of these, which exists on ion scales, is the CES mirror instability, which we already discussed in § 4.3.1. The second is the CES electron mirror instability – we shall consider this instability in § 4.3.4.
4.3.3. Parallel transverse instability
As was shown in § 4.2, in the limit ![]() $\varDelta _e \beta _e \gg 1$, the fastest-growing CES microinstability is essentially unmagnetised, and is a variant of the so-called transverse instability (Kahn Reference Kahn1962, Reference Kahn1964; Albright Reference Albright1970b). This instability is also sometimes referred to as the resonant (electron) Weibel instability, or the Weibel instability at small anisotropy (Fried Reference Fried1959; Weibel Reference Weibel1959). Both the linear theory of this instability and its physical mechanism have been explored extensively for bi-Maxwellian plasmas (see, e.g. Lazar et al. Reference Lazar, Schlickeiser and Poedts2009; Ibscher et al. Reference Ibscher, Lazar and Schlickeiser2012), and various studies (both analytical and numerical) of its nonlinear evolution have also been performed (Albright Reference Albright1970a; Davidson et al. Reference Davidson, Hammer, Haber and Wagner1972; Lemons et al. Reference Lemons, Winske and Gary1979; Califano et al. Reference Califano, Pegoraro, Bulanov and Mangeney1998, Reference Califano, Cecchi and Chiuderi2002; Kato Reference Kato2005; Pokhotelov & Amariutei Reference Pokhotelov and Amariutei2011; Ruyer et al. Reference Ruyer, Gremillet, Debayle and Bonnaud2015). For the small anisotropy case that is relevant to CE plasma, the mechanism of the instability is somewhat subtle, involving both non-resonant and Landau-resonant wave–particle interactions. In a Maxwellian plasma, transverse modes are non-propagating and Landau-damped by electrons with velocities
$\varDelta _e \beta _e \gg 1$, the fastest-growing CES microinstability is essentially unmagnetised, and is a variant of the so-called transverse instability (Kahn Reference Kahn1962, Reference Kahn1964; Albright Reference Albright1970b). This instability is also sometimes referred to as the resonant (electron) Weibel instability, or the Weibel instability at small anisotropy (Fried Reference Fried1959; Weibel Reference Weibel1959). Both the linear theory of this instability and its physical mechanism have been explored extensively for bi-Maxwellian plasmas (see, e.g. Lazar et al. Reference Lazar, Schlickeiser and Poedts2009; Ibscher et al. Reference Ibscher, Lazar and Schlickeiser2012), and various studies (both analytical and numerical) of its nonlinear evolution have also been performed (Albright Reference Albright1970a; Davidson et al. Reference Davidson, Hammer, Haber and Wagner1972; Lemons et al. Reference Lemons, Winske and Gary1979; Califano et al. Reference Califano, Pegoraro, Bulanov and Mangeney1998, Reference Califano, Cecchi and Chiuderi2002; Kato Reference Kato2005; Pokhotelov & Amariutei Reference Pokhotelov and Amariutei2011; Ruyer et al. Reference Ruyer, Gremillet, Debayle and Bonnaud2015). For the small anisotropy case that is relevant to CE plasma, the mechanism of the instability is somewhat subtle, involving both non-resonant and Landau-resonant wave–particle interactions. In a Maxwellian plasma, transverse modes are non-propagating and Landau-damped by electrons with velocities ![]() $v \approx \omega /k_{\|}$. However, this damping can be reversed by the free energy associated with positive electron-pressure anisotropy at wavenumbers that satisfy
$v \approx \omega /k_{\|}$. However, this damping can be reversed by the free energy associated with positive electron-pressure anisotropy at wavenumbers that satisfy ![]() $k d_e \lesssim \varDelta _e^{1/2}$; the electron Landau damping increases more rapidly with
$k d_e \lesssim \varDelta _e^{1/2}$; the electron Landau damping increases more rapidly with ![]() $k$ than the instability's drive, which in turn sets the wavenumber at which peak growth occurs. The requirement for the corresponding scale to be well below the electron-Larmor scale – and thus for the plasma to be quasi-unmagnetised with respect to the transverse modes – sets the restriction
$k$ than the instability's drive, which in turn sets the wavenumber at which peak growth occurs. The requirement for the corresponding scale to be well below the electron-Larmor scale – and thus for the plasma to be quasi-unmagnetised with respect to the transverse modes – sets the restriction ![]() $\varDelta _e \beta _e \gg 1$ on the instability's operation. In general, transverse modes whose wavevectors are co-parallel to the velocity-space direction along which the temperature is smallest are the fastest growing; in the case of a CE electron distribution function of the form (4.1) with
$\varDelta _e \beta _e \gg 1$ on the instability's operation. In general, transverse modes whose wavevectors are co-parallel to the velocity-space direction along which the temperature is smallest are the fastest growing; in the case of a CE electron distribution function of the form (4.1) with ![]() $\varDelta _e > 0$, these modes’ wavevectors are parallel to the magnetic field. However, a broad spectrum of oblique transverse modes is also destabilised when
$\varDelta _e > 0$, these modes’ wavevectors are parallel to the magnetic field. However, a broad spectrum of oblique transverse modes is also destabilised when ![]() $\varDelta _e > 0$.
$\varDelta _e > 0$.
To characterise the transverse instability's growth analytically, we first assume ![]() $\varDelta _e \beta _e \gg 1$, and then take directly the unmagnetised limit of the full CES dispersion relation (see Appendix K.3.4) under the orderings
$\varDelta _e \beta _e \gg 1$, and then take directly the unmagnetised limit of the full CES dispersion relation (see Appendix K.3.4) under the orderings
We obtain two non-propagating modes (real frequency ![]() $\varpi = 0$) that have growth rates
$\varpi = 0$) that have growth rates
 $$\begin{align} \gamma_1 &= \frac{k v_{\mathrm{th}e}}{\sqrt{\rm \pi}} \left(\varDelta_e \frac{k_{\|}^2-k_{\bot}^2}{k^2} - \frac{k^2 \rho_e^2}{\beta_e}\right) , \end{align}$$
$$\begin{align} \gamma_1 &= \frac{k v_{\mathrm{th}e}}{\sqrt{\rm \pi}} \left(\varDelta_e \frac{k_{\|}^2-k_{\bot}^2}{k^2} - \frac{k^2 \rho_e^2}{\beta_e}\right) , \end{align}$$ $$\begin{align}\gamma_2 &= \frac{k v_{\mathrm{th}e}}{\sqrt{\rm \pi}} \left(\varDelta_e \frac{k_{\|}^2}{k^2} - \frac{k^2 \rho_e^2}{\beta_e}\right) . \end{align}$$
$$\begin{align}\gamma_2 &= \frac{k v_{\mathrm{th}e}}{\sqrt{\rm \pi}} \left(\varDelta_e \frac{k_{\|}^2}{k^2} - \frac{k^2 \rho_e^2}{\beta_e}\right) . \end{align}$$
For ![]() $\varDelta _e > 0$, the growth rate of the second mode is always positive and larger than that of the first mode; the first mode only has a positive growth rate provided
$\varDelta _e > 0$, the growth rate of the second mode is always positive and larger than that of the first mode; the first mode only has a positive growth rate provided ![]() $k_{\bot } < k_{\|}$. Now taking the subsidiary limit
$k_{\bot } < k_{\|}$. Now taking the subsidiary limit ![]() $k_{\|} \rho _e \gg k_{\bot } \rho _e \gg 1$, we find that both roots have the same growth rate
$k_{\|} \rho _e \gg k_{\bot } \rho _e \gg 1$, we find that both roots have the same growth rate
 \begin{equation} \gamma \approx \frac{k_{\|} v_{\mathrm{th}e}}{\sqrt{\rm \pi}} \left(\varDelta_e - \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right) , \end{equation}
\begin{equation} \gamma \approx \frac{k_{\|} v_{\mathrm{th}e}}{\sqrt{\rm \pi}} \left(\varDelta_e - \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right) , \end{equation}
which is identical to (4.24b). We note by comparison with (4.24a) that the unmagnetised limit fails to recover the non-zero real frequencies of the ![]() $k_{\|} \rho _e \gg 1$ whistler modes; this is because the ratio of these modes’ real frequency
$k_{\|} \rho _e \gg 1$ whistler modes; this is because the ratio of these modes’ real frequency ![]() $\varpi$ to their growth rate
$\varpi$ to their growth rate ![]() $\gamma$ is
$\gamma$ is ![]() $\varpi /\gamma \sim 1/k_{\|} \rho _e \ll 1$.
$\varpi /\gamma \sim 1/k_{\|} \rho _e \ll 1$.
The maximum growth rate ![]() $\gamma _{\mathrm {max}}$ of the second mode (4.29b) for an oblique wavevector with angle
$\gamma _{\mathrm {max}}$ of the second mode (4.29b) for an oblique wavevector with angle ![]() $\theta$ is
$\theta$ is
attained at the (total) wavenumber
 \begin{equation} (k
\rho_e)_{\mathrm{peak}} = \cos{\theta} \left(\frac{\varDelta_e
\beta_e}{3}\right)^{1/2}.
\end{equation}
\begin{equation} (k
\rho_e)_{\mathrm{peak}} = \cos{\theta} \left(\frac{\varDelta_e
\beta_e}{3}\right)^{1/2}.
\end{equation}The parallel and perpendicular wavenumbers of this maximum growth are then
 \begin{align}
(k_{\|}
\rho_e)_{\mathrm{peak}} = \cos^2{\theta} \left(\frac{\varDelta_e
\beta_e}{3}\right)^{1/2} , \quad (k_{\bot} \rho_e)_{\mathrm{peak}}
= \cos{\theta} \sin{\theta} \left(\frac{\varDelta_e \beta_e}{3}\right)^{1/2} .
\end{align}
\begin{align}
(k_{\|}
\rho_e)_{\mathrm{peak}} = \cos^2{\theta} \left(\frac{\varDelta_e
\beta_e}{3}\right)^{1/2} , \quad (k_{\bot} \rho_e)_{\mathrm{peak}}
= \cos{\theta} \sin{\theta} \left(\frac{\varDelta_e \beta_e}{3}\right)^{1/2} .
\end{align}
In the special case of parallel modes (![]() $\theta = 0^{\circ }$), this recovers the peak growth rate (4.25) of the CES whistler instability at
$\theta = 0^{\circ }$), this recovers the peak growth rate (4.25) of the CES whistler instability at ![]() $k_{\|}$ in the limit
$k_{\|}$ in the limit ![]() $\varDelta _e \beta _e \gg 1$.
$\varDelta _e \beta _e \gg 1$.
In figure 15, we demonstrate that the fastest-growing unstable modes in the limit ![]() $\varDelta _e \beta _e \gg 1$ are indeed transverse ones. This figure shows the numerically determined growth rate as a function of
$\varDelta _e \beta _e \gg 1$ are indeed transverse ones. This figure shows the numerically determined growth rate as a function of ![]() $k_{\|}$ and
$k_{\|}$ and ![]() $k_{\perp })$, for a particular large value of
$k_{\perp })$, for a particular large value of ![]() $\varDelta _e \beta _e$. A broad range of sub-electron-Larmor-scale modes are unstable (figure 15a), with the parallel wavenumber of the fastest-growing ones closely agreeing with the analytical prediction (4.33a,b). The analytical expression (4.29b) for the transverse instability's growth rate also agrees well with the numerical result as a function of both
$\varDelta _e \beta _e$. A broad range of sub-electron-Larmor-scale modes are unstable (figure 15a), with the parallel wavenumber of the fastest-growing ones closely agreeing with the analytical prediction (4.33a,b). The analytical expression (4.29b) for the transverse instability's growth rate also agrees well with the numerical result as a function of both ![]() $k_{\|}$ and
$k_{\|}$ and ![]() $k_{\perp }$ (figure 15b).
$k_{\perp }$ (figure 15b).

Figure 15. Oblique unstable modes at ![]() $\varDelta _e \beta _e \gg 1$. (a) Maximum positive growth rates of linear perturbations resulting from CE ion- and electron-shear terms in the CE distribution function (4.1) for
$\varDelta _e \beta _e \gg 1$. (a) Maximum positive growth rates of linear perturbations resulting from CE ion- and electron-shear terms in the CE distribution function (4.1) for ![]() $\varDelta _e \beta _e = 100$. Here, a temperature-equilibrated hydrogen plasma is considered, viz.
$\varDelta _e \beta _e = 100$. Here, a temperature-equilibrated hydrogen plasma is considered, viz. ![]() $\varDelta _e = \mu _e^{1/2} \varDelta _i$ and
$\varDelta _e = \mu _e^{1/2} \varDelta _i$ and ![]() $\beta _i = \beta _e$. The growth rates of all modes are calculated in the same way as figure 14. The vertical dashed line indicates the value of
$\beta _i = \beta _e$. The growth rates of all modes are calculated in the same way as figure 14. The vertical dashed line indicates the value of ![]() $k_{\|} \rho _e$ at which maximum growth of the parallel transverse instability is attained (see (4.33a,b)), while the horizontal one indicates
$k_{\|} \rho _e$ at which maximum growth of the parallel transverse instability is attained (see (4.33a,b)), while the horizontal one indicates ![]() $k_{\perp } \rho _e = 1$. (b) The transverse mode's growth rate (solid line) as a function of
$k_{\perp } \rho _e = 1$. (b) The transverse mode's growth rate (solid line) as a function of ![]() $k_{\|} \rho _e$ with
$k_{\|} \rho _e$ with ![]() $k_{\bot } \rho _e = 1$ (top), and as a function of
$k_{\bot } \rho _e = 1$ (top), and as a function of ![]() $k_{\perp } \rho _e$ with
$k_{\perp } \rho _e$ with ![]() $k_{\|} \rho _e = (\varDelta _e \beta _e/3)^{1/2}$ (bottom). The dashed lines show the analytical prediction (4.29b) for this quantity.
$k_{\|} \rho _e = (\varDelta _e \beta _e/3)^{1/2}$ (bottom). The dashed lines show the analytical prediction (4.29b) for this quantity.
4.3.4. Electron mirror instability
The oblique microinstability evident in figure 14(b) at sub-ion-Larmor scales is the CES electron mirror instability: the destabilisation of KAWs by excess perpendicular electron pressure (viz. ![]() $\varDelta _e > 0$) associated with the CE electron-shear term. The instability (which has also been referred to as the field-swelling instability – see Basu & Coppi Reference Basu and Coppi1984) is perhaps confusingly named, given that its physical mechanism is rather different to that of the (ion-scale) mirror instability: non-resonant interactions between the anisotropic distribution of electrons and the KAWs causes the restoring force underpinning the latter's characteristic oscillation to be negated if
$\varDelta _e > 0$) associated with the CE electron-shear term. The instability (which has also been referred to as the field-swelling instability – see Basu & Coppi Reference Basu and Coppi1984) is perhaps confusingly named, given that its physical mechanism is rather different to that of the (ion-scale) mirror instability: non-resonant interactions between the anisotropic distribution of electrons and the KAWs causes the restoring force underpinning the latter's characteristic oscillation to be negated if ![]() $\varDelta _e > 1/\beta _e$. The electron mirror instability has been extensively explored in
$\varDelta _e > 1/\beta _e$. The electron mirror instability has been extensively explored in ![]() $\beta _e \sim 1$ plasma (see Hellinger & Štverák (Reference Hellinger and Štverák2018), and references therein); in plasmas with
$\beta _e \sim 1$ plasma (see Hellinger & Štverák (Reference Hellinger and Štverák2018), and references therein); in plasmas with ![]() $\beta _e \gg 1$, it has been analytically characterised and its physical mechanism elucidated in the quasi-perpendicular (
$\beta _e \gg 1$, it has been analytically characterised and its physical mechanism elucidated in the quasi-perpendicular (![]() $k_{\|} \ll k_{\perp }$) limit of gyrokinetics (Kunz et al. Reference Kunz, Abel, Klein and Schekochihin2018). Here, we find that once its marginality condition (
$k_{\|} \ll k_{\perp }$) limit of gyrokinetics (Kunz et al. Reference Kunz, Abel, Klein and Schekochihin2018). Here, we find that once its marginality condition (![]() $\varDelta _e = 1/\beta _e$) is surpassed sufficiently, oblique modes with
$\varDelta _e = 1/\beta _e$) is surpassed sufficiently, oblique modes with ![]() $k_{\|} \lesssim k_{\perp }$ are also destabilised.
$k_{\|} \lesssim k_{\perp }$ are also destabilised.
As with the mirror instability, a simple analytic characterisation of the CES electron mirror instability can be performed in the case of marginal instability. We define the marginality parameter ![]() $\varGamma _e \equiv \varDelta _e \beta _e -1$, and adopt the ordering
$\varGamma _e \equiv \varDelta _e \beta _e -1$, and adopt the ordering
with the additional assumption that ![]() $\varGamma _e \gg \mu _e^{1/2}$ in order that the effect of ion-pressure anisotropy can be neglected. Then, it can be shown (see Appendix K.3.5) that the growth rate is
$\varGamma _e \gg \mu _e^{1/2}$ in order that the effect of ion-pressure anisotropy can be neglected. Then, it can be shown (see Appendix K.3.5) that the growth rate is
 \begin{equation} \frac{\gamma}{\varOmega_e} = \frac{k_{\|} \rho_e}{\beta_e} \left[-\frac{3\sqrt{\rm \pi}}{4} k_{{\perp}}^2 \rho_e^2+ \sqrt{\frac{3}{2} \varGamma_e k_{{\perp}}^2 \rho_e^2 -\frac{9}{4} k_{\|}^2 \rho_e^2 + \frac{9}{16}\left({\rm \pi}-2\right) k_{{\perp}}^4 \rho_e^4 } \right] . \end{equation}
\begin{equation} \frac{\gamma}{\varOmega_e} = \frac{k_{\|} \rho_e}{\beta_e} \left[-\frac{3\sqrt{\rm \pi}}{4} k_{{\perp}}^2 \rho_e^2+ \sqrt{\frac{3}{2} \varGamma_e k_{{\perp}}^2 \rho_e^2 -\frac{9}{4} k_{\|}^2 \rho_e^2 + \frac{9}{16}\left({\rm \pi}-2\right) k_{{\perp}}^4 \rho_e^4 } \right] . \end{equation}It follows that the maximum growth rate is
 \begin{align} \gamma_{\rm max} & = \frac{\left[{\rm \pi}-8+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}\right]^{3/2}}{48\left({\rm \pi}-2\right)} \left[ \sqrt{\frac{{\rm \pi}+4+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}}{{\rm \pi}-8+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}}}-\sqrt{\frac{\rm \pi}{{\rm \pi}-2}}\right] \frac{\varGamma_e^2}{\beta_e} \varOmega_e \nonumber\\ & \approx 0.055 \frac{\varGamma_e^2}{\beta_e} \varOmega_e , \end{align}
\begin{align} \gamma_{\rm max} & = \frac{\left[{\rm \pi}-8+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}\right]^{3/2}}{48\left({\rm \pi}-2\right)} \left[ \sqrt{\frac{{\rm \pi}+4+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}}{{\rm \pi}-8+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}}}-\sqrt{\frac{\rm \pi}{{\rm \pi}-2}}\right] \frac{\varGamma_e^2}{\beta_e} \varOmega_e \nonumber\\ & \approx 0.055 \frac{\varGamma_e^2}{\beta_e} \varOmega_e , \end{align}attained at
 $$\begin{align} (k_\| \rho_e)_{\mathrm{peak}} &= \sqrt{\frac{{\rm \pi}-8+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}}{36\left({\rm \pi}-2\right)}} \varGamma_e \approx 0.27 \varGamma_e, \end{align}$$
$$\begin{align} (k_\| \rho_e)_{\mathrm{peak}} &= \sqrt{\frac{{\rm \pi}-8+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}}{36\left({\rm \pi}-2\right)}} \varGamma_e \approx 0.27 \varGamma_e, \end{align}$$ $$\begin{align}(k_\perp \rho_e)_{\mathrm{peak}} &= \sqrt{\frac{{\rm \pi}-8+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}}{6\left({\rm \pi}-2\right)}} \varGamma_e^{1/2} \approx 0.65 \varGamma_e^{1/2}. \end{align}$$
$$\begin{align}(k_\perp \rho_e)_{\mathrm{peak}} &= \sqrt{\frac{{\rm \pi}-8+\sqrt{{\rm \pi}\left(16+{\rm \pi}\right)}}{6\left({\rm \pi}-2\right)}} \varGamma_e^{1/2} \approx 0.65 \varGamma_e^{1/2}. \end{align}$$
Figure 16 demonstrates that these predictions are accurate by comparing them with numerical results for a particular (small) value of ![]() $\varGamma _e$. More specifically, figure 16(a) shows that the location in the
$\varGamma _e$. More specifically, figure 16(a) shows that the location in the ![]() $(k_{\|},k_{\perp })$ plane at which the maximum growth of the electron mirror instability is attained closely matches the analytical prediction (4.37), while figure 16(b) confirms that the wavenumber dependence of the growth rate agrees with (4.35) for
$(k_{\|},k_{\perp })$ plane at which the maximum growth of the electron mirror instability is attained closely matches the analytical prediction (4.37), while figure 16(b) confirms that the wavenumber dependence of the growth rate agrees with (4.35) for ![]() $k_{\perp } \rho _e \gtrsim \mu _e^{1/4}$. We note that, in addition to the electron mirror, another instability operating at smaller characteristic values of
$k_{\perp } \rho _e \gtrsim \mu _e^{1/4}$. We note that, in addition to the electron mirror, another instability operating at smaller characteristic values of ![]() $k_{\perp } \rho _e$ is evident in figure 16. These are the
$k_{\perp } \rho _e$ is evident in figure 16. These are the ![]() $k_{\perp } \rho _i \gtrsim 1$ mirror modes driven unstable by the CE ion-shear term that were discussed in § 4.3.1; for
$k_{\perp } \rho _i \gtrsim 1$ mirror modes driven unstable by the CE ion-shear term that were discussed in § 4.3.1; for ![]() $1 \ll k \rho _i \ll \mu _e^{-1/4}$, the ion-pressure anisotropy associated with the CE ion-shear terms remains a greater free-energy source for KAW instabilities than the CE electron-shear term, even when
$1 \ll k \rho _i \ll \mu _e^{-1/4}$, the ion-pressure anisotropy associated with the CE ion-shear terms remains a greater free-energy source for KAW instabilities than the CE electron-shear term, even when ![]() $\varDelta _e > 1/\beta _e$.
$\varDelta _e > 1/\beta _e$.

Figure 16. Electron mirror instability at ![]() $\varGamma _e = \varDelta _e \beta _e -1 \ll 1$. (a) Growth rates of unstable electron mirror modes associated with the CE distribution function (4.1) for
$\varGamma _e = \varDelta _e \beta _e -1 \ll 1$. (a) Growth rates of unstable electron mirror modes associated with the CE distribution function (4.1) for ![]() $\varGamma _e= 1/3$ (
$\varGamma _e= 1/3$ (![]() $\varDelta _e \beta _e = 4/3$). The growth rates of all modes are calculated in the same way as figure 14. The dashed white lines indicate the analytical prediction (4.37) for the parallel/perpendicular wavenumber at which peak growth is achieved. (b) Plot of the electron mirror mode's growth rate (solid line) as a function of
$\varDelta _e \beta _e = 4/3$). The growth rates of all modes are calculated in the same way as figure 14. The dashed white lines indicate the analytical prediction (4.37) for the parallel/perpendicular wavenumber at which peak growth is achieved. (b) Plot of the electron mirror mode's growth rate (solid line) as a function of ![]() $k_{\|} \rho _e$ with
$k_{\|} \rho _e$ with ![]() $k_{\bot } \rho _e = 0.65 \varGamma _e^{1/2}$ (top), and as a function of
$k_{\bot } \rho _e = 0.65 \varGamma _e^{1/2}$ (top), and as a function of ![]() $k_{\perp } \rho _e$ with
$k_{\perp } \rho _e$ with ![]() $k_{\|} \rho _e = 0.27 \varGamma _e$ (bottom). The dashed lines show the analytical prediction (4.35) for this quantity.
$k_{\|} \rho _e = 0.27 \varGamma _e$ (bottom). The dashed lines show the analytical prediction (4.35) for this quantity.
For ![]() $\varGamma _e \gtrsim 1$, our near-marginal theory anticipates that peak growth occurs at electron-Larmor scales (
$\varGamma _e \gtrsim 1$, our near-marginal theory anticipates that peak growth occurs at electron-Larmor scales (![]() $k_{\|} \rho _e \lesssim k_{\perp } \rho _e \sim 1$), with
$k_{\|} \rho _e \lesssim k_{\perp } \rho _e \sim 1$), with ![]() $\gamma _{\rm max} \sim \varOmega _e/\beta _e$. These expectations are indeed realised numerically, as shown in figure 17 (see also figure 14). The expression (4.35) for the growth rate as a function of wavenumber that was derived in the case of
$\gamma _{\rm max} \sim \varOmega _e/\beta _e$. These expectations are indeed realised numerically, as shown in figure 17 (see also figure 14). The expression (4.35) for the growth rate as a function of wavenumber that was derived in the case of ![]() $\varGamma _e \ll 1$ remains qualitatively – but not quantitatively – accurate (see figure 17b). Figure 18 shows that a similar conclusion holds for the expression (4.36) for the peak growth rate, and also for the expressions (4.37a) and (4.37b) of the parallel and perpendicular wavenumbers at which that growth occurs.
$\varGamma _e \ll 1$ remains qualitatively – but not quantitatively – accurate (see figure 17b). Figure 18 shows that a similar conclusion holds for the expression (4.36) for the peak growth rate, and also for the expressions (4.37a) and (4.37b) of the parallel and perpendicular wavenumbers at which that growth occurs.

Figure 17. Electron mirror instability at ![]() $\varGamma _e = \varDelta _e \beta _e -1 \sim 1$. (a) Growth rates of unstable electron mirror modes associated with the CE distribution function (4.1) for
$\varGamma _e = \varDelta _e \beta _e -1 \sim 1$. (a) Growth rates of unstable electron mirror modes associated with the CE distribution function (4.1) for ![]() $\varGamma _e = 1$ (
$\varGamma _e = 1$ (![]() $\varDelta _e \beta _e = 2$). The growth rates of all modes are calculated in the same way as figure 14. The dashed white lines indicate the analytical prediction (4.37) for the parallel/perpendicular wavenumber at which peak growth is achieved, while the dotted line indicates the analytical prediction (4.43) for the total wavenumber below which oblique long-wavelength (
$\varDelta _e \beta _e = 2$). The growth rates of all modes are calculated in the same way as figure 14. The dashed white lines indicate the analytical prediction (4.37) for the parallel/perpendicular wavenumber at which peak growth is achieved, while the dotted line indicates the analytical prediction (4.43) for the total wavenumber below which oblique long-wavelength (![]() $k_{\|} \rho _e < k_{\perp } \rho _e \ll 1$) electron mirror modes become unstable. (b) The electron mirror mode's growth rate (solid line) as a function of
$k_{\|} \rho _e < k_{\perp } \rho _e \ll 1$) electron mirror modes become unstable. (b) The electron mirror mode's growth rate (solid line) as a function of ![]() $k_{\|} \rho _e$ with
$k_{\|} \rho _e$ with ![]() $k_{\bot } \rho _e = 0.65 \varGamma _e^{1/2}$ (top), and as a function of
$k_{\bot } \rho _e = 0.65 \varGamma _e^{1/2}$ (top), and as a function of ![]() $k_{\perp } \rho _e$ with
$k_{\perp } \rho _e$ with ![]() $k_{\|} \rho _e = 0.27 \varGamma _e$ (bottom). The dashed lines show the analytical prediction (4.35) for this quantity.
$k_{\|} \rho _e = 0.27 \varGamma _e$ (bottom). The dashed lines show the analytical prediction (4.35) for this quantity.

Figure 18. The maximum growth of the electron mirror instability. The maximum normalised growth rate ![]() $\gamma _e \beta _e/\varOmega _e$ ((a), solid red line) of unstable electron mirror modes as a function of
$\gamma _e \beta _e/\varOmega _e$ ((a), solid red line) of unstable electron mirror modes as a function of ![]() $\varDelta _e \beta _e$, as well as parallel ((b), solid blue line) and perpendicular ((c), solid yellow line) wavenumbers,
$\varDelta _e \beta _e$, as well as parallel ((b), solid blue line) and perpendicular ((c), solid yellow line) wavenumbers, ![]() $(k_{\|} \rho _e)_{\mathrm {peak}}$ and
$(k_{\|} \rho _e)_{\mathrm {peak}}$ and ![]() $(k_{\perp } \rho _e)_{\mathrm {peak}}$, respectively, at which that growth is attained. The analytical prediction (4.36) of
$(k_{\perp } \rho _e)_{\mathrm {peak}}$, respectively, at which that growth is attained. The analytical prediction (4.36) of ![]() $\gamma _{\rm max}$ for marginally unstable electron mirror modes, as well as the analogous predictions (4.37) for
$\gamma _{\rm max}$ for marginally unstable electron mirror modes, as well as the analogous predictions (4.37) for ![]() $(k_{\|} \rho _e)_{\mathrm {peak}}$ and
$(k_{\|} \rho _e)_{\mathrm {peak}}$ and ![]() $(k_{\perp } \rho _e)_{\mathrm {peak}}$, are shown as dashed lines. The dotted lines are the maximum growth rate and (parallel) wavenumber of peak growth for the CET parallel whistler instability (see § 4.3.2) as functions of
$(k_{\perp } \rho _e)_{\mathrm {peak}}$, are shown as dashed lines. The dotted lines are the maximum growth rate and (parallel) wavenumber of peak growth for the CET parallel whistler instability (see § 4.3.2) as functions of ![]() $\varDelta _e \beta _e$.
$\varDelta _e \beta _e$.
To confirm our prior claim in § 4.2 that the CES parallel whistler instability is faster growing than the electron mirror instability, we show the former's numerically computed growth rate on figure 18(a); as it approaches the asymptotic value (4.25) that is valid in the limit ![]() $\varDelta _e \beta _e \gg 1$, we observe that the electron mirror's growth rate is a factor of
$\varDelta _e \beta _e \gg 1$, we observe that the electron mirror's growth rate is a factor of ![]() ${\sim }3$ smaller (cf. figure 15a). The parallel wavenumber at which peak growth of the whistler instability occurs is also larger than the analogous quantity for the electron mirror by an order-unity factor.
${\sim }3$ smaller (cf. figure 15a). The parallel wavenumber at which peak growth of the whistler instability occurs is also larger than the analogous quantity for the electron mirror by an order-unity factor.
While we cannot derive a simple analytic expression for the growth rate of the dominant electron mirror modes when ![]() $\varGamma _e \gtrsim 1$, we can calculate this quantity for long-wavelength (viz.
$\varGamma _e \gtrsim 1$, we can calculate this quantity for long-wavelength (viz. ![]() $k \rho _e \ll 1$) modes. For this calculation, we assume that
$k \rho _e \ll 1$) modes. For this calculation, we assume that ![]() $k \rho _e \sim \mu _e^{1/4} \ll 1$,
$k \rho _e \sim \mu _e^{1/4} \ll 1$, ![]() $k_{\bot } \sim k_{\|}$ and the ordering
$k_{\bot } \sim k_{\|}$ and the ordering
Under these assumptions, we obtain (see Appendix K.3.5) two modes whose complex frequencies ![]() $\omega$ are given by
$\omega$ are given by
 \begin{align} \omega & \approx{\pm} k_\| \rho_e \varOmega_e \left\{\left[\frac{1}{\beta_e} + \varDelta_e\left(\frac{1}{2}- \mu_e^{1/2} \frac{k_{\|}^2 \rho_e^2- k_{\bot}^2 \rho_e^2}{k^4 \rho_e^4}\right) \right]\right.\nonumber\\ & \quad \times \left.\left[ \frac{k^2 \rho_e^2}{\beta_e} - \varDelta_e \left(k_{\bot}^2 \rho_e^2 + \mu_e^{1/2} \frac{k_{\|}^2}{k^2} - \frac{1}{2} k_{\|}^2 \rho_e^2 \right) \right]\right\}^{1/2} . \end{align}
\begin{align} \omega & \approx{\pm} k_\| \rho_e \varOmega_e \left\{\left[\frac{1}{\beta_e} + \varDelta_e\left(\frac{1}{2}- \mu_e^{1/2} \frac{k_{\|}^2 \rho_e^2- k_{\bot}^2 \rho_e^2}{k^4 \rho_e^4}\right) \right]\right.\nonumber\\ & \quad \times \left.\left[ \frac{k^2 \rho_e^2}{\beta_e} - \varDelta_e \left(k_{\bot}^2 \rho_e^2 + \mu_e^{1/2} \frac{k_{\|}^2}{k^2} - \frac{1}{2} k_{\|}^2 \rho_e^2 \right) \right]\right\}^{1/2} . \end{align}
The terms proportional to ![]() $\mu _e^{1/2} \varDelta _e$ are associated with the CE ion-shear term, which plays a non-negligible role for
$\mu _e^{1/2} \varDelta _e$ are associated with the CE ion-shear term, which plays a non-negligible role for ![]() $k \rho _e \lesssim \mu _e^{1/4}$. In the subsidiary limit
$k \rho _e \lesssim \mu _e^{1/4}$. In the subsidiary limit ![]() $k \rho _e \ll \mu _e^{1/4}$, (4.39) becomes the dispersion relation (4.18) obtained in § 4.3.1 for unstable mirror modes in the limit
$k \rho _e \ll \mu _e^{1/4}$, (4.39) becomes the dispersion relation (4.18) obtained in § 4.3.1 for unstable mirror modes in the limit ![]() $\varDelta _i \beta _i \gg 1$. In the opposite subsidiary limit
$\varDelta _i \beta _i \gg 1$. In the opposite subsidiary limit ![]() $k \rho _e \gg \mu _e^{1/4}$ (but
$k \rho _e \gg \mu _e^{1/4}$ (but ![]() $k \rho _e \ll 1$), (4.39) simplifies to
$k \rho _e \ll 1$), (4.39) simplifies to
 \begin{equation} \omega \approx{\pm} k_\| \rho_e \varOmega_e \sqrt{\left(\frac{1}{\beta_e} + \frac{\varDelta_e}{2}\right)\left[\frac{k^2 \rho_e^2}{\beta_e} - \varDelta_e \left(k_{\bot}^2 \rho_e^2 - \frac{1}{2} k_{\|}^2 \rho_e^2\right) \right]} . \end{equation}
\begin{equation} \omega \approx{\pm} k_\| \rho_e \varOmega_e \sqrt{\left(\frac{1}{\beta_e} + \frac{\varDelta_e}{2}\right)\left[\frac{k^2 \rho_e^2}{\beta_e} - \varDelta_e \left(k_{\bot}^2 \rho_e^2 - \frac{1}{2} k_{\|}^2 \rho_e^2\right) \right]} . \end{equation}
For ![]() $k_{\|} \ll k_{\perp }$, this recovers the high-
$k_{\|} \ll k_{\perp }$, this recovers the high-![]() $\beta$ limit of the dispersion relation for unstable KAWs previously derived in the gyrokinetic calculations of Kunz et al. (Reference Kunz, Abel, Klein and Schekochihin2018); our calculations show that this dispersion relation also applies to oblique (
$\beta$ limit of the dispersion relation for unstable KAWs previously derived in the gyrokinetic calculations of Kunz et al. (Reference Kunz, Abel, Klein and Schekochihin2018); our calculations show that this dispersion relation also applies to oblique (![]() $k_{\|} \lesssim k_{\perp }$) electron mirror modes. For
$k_{\|} \lesssim k_{\perp }$) electron mirror modes. For ![]() $\varDelta _e > 0$, we (as expected) have an unstable root if and only if
$\varDelta _e > 0$, we (as expected) have an unstable root if and only if
with the unstable mode's growth rate being
 \begin{equation} \gamma \approx k_\| \rho_e \varOmega_e \sqrt{\left(\frac{1}{\beta_e} + \frac{\varDelta_e}{2}\right)\left[\varDelta_e \left(k_{\bot}^2 \rho_e^2 - \frac{1}{2} k_{\|}^2 \rho_e^2\right) - \frac{k^2 \rho_e^2}{\beta_e} \right]} . \end{equation}
\begin{equation} \gamma \approx k_\| \rho_e \varOmega_e \sqrt{\left(\frac{1}{\beta_e} + \frac{\varDelta_e}{2}\right)\left[\varDelta_e \left(k_{\bot}^2 \rho_e^2 - \frac{1}{2} k_{\|}^2 \rho_e^2\right) - \frac{k^2 \rho_e^2}{\beta_e} \right]} . \end{equation} We can now provide an analytical demonstration that a broad spectrum of electron mirror modes is unstable if ![]() $\varGamma _e \gtrsim 1$. It follows directly from (4.39) that instability arises for all modes with
$\varGamma _e \gtrsim 1$. It follows directly from (4.39) that instability arises for all modes with ![]() $k_{\perp } > k_{\|}$ if the following constraint on the total wavenumber
$k_{\perp } > k_{\|}$ if the following constraint on the total wavenumber ![]() $k$ is satisfied:
$k$ is satisfied:
 \begin{equation} k \rho_i < \sqrt{\frac{2 \mu_e^{1/2} \left(\varGamma_e+1\right) \cos^2{\theta}}{\left(\varGamma_e+3\right) \cos^2{\theta}-2 \varGamma_e \sin^2{\theta}}} , \end{equation}
\begin{equation} k \rho_i < \sqrt{\frac{2 \mu_e^{1/2} \left(\varGamma_e+1\right) \cos^2{\theta}}{\left(\varGamma_e+3\right) \cos^2{\theta}-2 \varGamma_e \sin^2{\theta}}} , \end{equation}
where ![]() $\theta = \tan ^{-1}{(k_{\perp }/k_{\|})}$ is, as normal, the wavevector angle. The validity of this bound is illustrated in figure 17(a). (4.43) is particularly simple to interpret in the subsidiary limit
$\theta = \tan ^{-1}{(k_{\perp }/k_{\|})}$ is, as normal, the wavevector angle. The validity of this bound is illustrated in figure 17(a). (4.43) is particularly simple to interpret in the subsidiary limit ![]() $k \rho _e \gg \mu _e^{1/4}$, yielding a lower bound on
$k \rho _e \gg \mu _e^{1/4}$, yielding a lower bound on ![]() $\theta$ alone:
$\theta$ alone:
For ![]() $\varGamma _e \ll 1$ (but
$\varGamma _e \ll 1$ (but ![]() $\varGamma _e > 0$), this implies that the only unstable electron mirror modes are quasi-perpendicular, as anticipated from our calculations pertaining to the marginal state of the instability. On the other hand, for
$\varGamma _e > 0$), this implies that the only unstable electron mirror modes are quasi-perpendicular, as anticipated from our calculations pertaining to the marginal state of the instability. On the other hand, for ![]() $\varGamma _e \gtrsim 1$, modes with a wide range of wavevector angles will be destabilised.
$\varGamma _e \gtrsim 1$, modes with a wide range of wavevector angles will be destabilised.
4.4. CES microinstability classification: negative pressure anisotropy  $(\epsilon _i < 0)$
$(\epsilon _i < 0)$
4.4.1. Firehose instability
The best-known instability to be triggered by either negative ion or electron-pressure anisotropy associated with the CE ion- and electron-shear terms, respectively, is the CES firehose instability. The linear theory of the firehose (or garden-hose) instability in high-![]() $\beta$ plasma, the first studies of which were completed over half a century ago (Rosenbluth Reference Rosenbluth1956; Chandrasekhar et al. Reference Chandrasekhar, Kaufman and Watson1958; Parker Reference Parker1958; Vedenov & Sagdeev Reference Vedenov and Sagdeev1958), has previously been explored in the contexts of plasmas with bi-Maxwellian distributions (e.g. Kennel & Sagdeev Reference Kennel and Sagdeev1967; Davidson & Völk Reference Davidson and Völk1968; Yoon, Wu & de Assis Reference Yoon, Wu and de Assis1993; Hellinger & Matsumoto Reference Hellinger and Matsumoto2000), CE distributions (e.g. Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005) and even characterisations that are independent of the ion distribution function (e.g. Schekochihin et al. Reference Schekochihin, Cowley, Rincon and Rosin2010; Kunz et al. Reference Kunz, Schekochihin, Chen, Abel and Cowley2015). Its physical mechanism is well established: negative pressure anisotropies reduce the elasticity of magnetic-field lines that gives rise to Alfvén waves, and can completely reverse it when
$\beta$ plasma, the first studies of which were completed over half a century ago (Rosenbluth Reference Rosenbluth1956; Chandrasekhar et al. Reference Chandrasekhar, Kaufman and Watson1958; Parker Reference Parker1958; Vedenov & Sagdeev Reference Vedenov and Sagdeev1958), has previously been explored in the contexts of plasmas with bi-Maxwellian distributions (e.g. Kennel & Sagdeev Reference Kennel and Sagdeev1967; Davidson & Völk Reference Davidson and Völk1968; Yoon, Wu & de Assis Reference Yoon, Wu and de Assis1993; Hellinger & Matsumoto Reference Hellinger and Matsumoto2000), CE distributions (e.g. Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005) and even characterisations that are independent of the ion distribution function (e.g. Schekochihin et al. Reference Schekochihin, Cowley, Rincon and Rosin2010; Kunz et al. Reference Kunz, Schekochihin, Chen, Abel and Cowley2015). Its physical mechanism is well established: negative pressure anisotropies reduce the elasticity of magnetic-field lines that gives rise to Alfvén waves, and can completely reverse it when ![]() $\varDelta _i$ is negative enough. The long-wavelength ‘fluid’ firehose instability (whose mechanism is independent of the particular ion distribution function) is non-resonant in nature; however, resonant damping mechanisms such as Barnes damping or cyclotron damping play an important role in regulating the growth of modes on scales comparable to the ion-Larmor scale, and thereby set the scale of peak firehose growth. Beyond linear theory, nonlinear analytical studies of the parallel firehose instability in high-
$\varDelta _i$ is negative enough. The long-wavelength ‘fluid’ firehose instability (whose mechanism is independent of the particular ion distribution function) is non-resonant in nature; however, resonant damping mechanisms such as Barnes damping or cyclotron damping play an important role in regulating the growth of modes on scales comparable to the ion-Larmor scale, and thereby set the scale of peak firehose growth. Beyond linear theory, nonlinear analytical studies of the parallel firehose instability in high-![]() $\beta$ plasma have been completed (e.g. Rosin et al. Reference Rosin, Schekochihin, Rincon and Cowley2011), as well as numerical ones (e.g. Kunz et al. Reference Kunz, Schekochihin and Stone2014; Melville et al. Reference Melville, Schekochihin and Kunz2016; Riquelme et al. Reference Riquelme, Quataert and Verscharen2018).
$\beta$ plasma have been completed (e.g. Rosin et al. Reference Rosin, Schekochihin, Rincon and Cowley2011), as well as numerical ones (e.g. Kunz et al. Reference Kunz, Schekochihin and Stone2014; Melville et al. Reference Melville, Schekochihin and Kunz2016; Riquelme et al. Reference Riquelme, Quataert and Verscharen2018).
While there is much in common between firehose modes across all wavevector angles, there are certain differences that, on account of their significance for determining the fastest-growing firehose mode, are important to highlight. Based on these differences, firehose modes can be categorised into three different types: quasi-parallel, oblique and critical-line firehose modes. Quasi-parallel firehose modes, which are destabilised left-handed and/or right-handed high-![]() $\beta$ Alfvén waves (Kennel & Sagdeev Reference Kennel and Sagdeev1967; Davidson & Völk Reference Davidson and Völk1968), exist inside a narrow cone of wavevector angles
$\beta$ Alfvén waves (Kennel & Sagdeev Reference Kennel and Sagdeev1967; Davidson & Völk Reference Davidson and Völk1968), exist inside a narrow cone of wavevector angles ![]() $\theta \lesssim \beta _i^{-1/4}$ (Achterberg Reference Achterberg2013). The peak wavenumber of their growth (
$\theta \lesssim \beta _i^{-1/4}$ (Achterberg Reference Achterberg2013). The peak wavenumber of their growth (![]() $k_{\|} \rho _i \sim |\varDelta _i + 2/\beta _i|^{1/2}$) is determined by gyroviscosity, an FLR effect (Schekochihin et al. Reference Schekochihin, Cowley, Rincon and Rosin2010). For
$k_{\|} \rho _i \sim |\varDelta _i + 2/\beta _i|^{1/2}$) is determined by gyroviscosity, an FLR effect (Schekochihin et al. Reference Schekochihin, Cowley, Rincon and Rosin2010). For ![]() $\theta \gtrsim \beta _i^{-1/4}$, the characteristic low-frequency (viz.
$\theta \gtrsim \beta _i^{-1/4}$, the characteristic low-frequency (viz. ![]() $\omega \ll \varOmega _i$) waves that exist above ion-Larmor-scales in high-
$\omega \ll \varOmega _i$) waves that exist above ion-Larmor-scales in high-![]() $\beta$ plasma are shear-Alfvén waves and (compressible) slow modes; the former remains susceptible to firehose instability, but, on account of its FLR coupling to the slow mode, its instability proceeds quite differently at sufficiently small wavenumbers (
$\beta$ plasma are shear-Alfvén waves and (compressible) slow modes; the former remains susceptible to firehose instability, but, on account of its FLR coupling to the slow mode, its instability proceeds quite differently at sufficiently small wavenumbers (![]() $k \rho _i \gtrsim |\varDelta _i + 2/\beta _i|^{1/2}$), with peak growth occurring at smaller scales (
$k \rho _i \gtrsim |\varDelta _i + 2/\beta _i|^{1/2}$), with peak growth occurring at smaller scales (![]() $k_{\|} \rho _i \sim |\varDelta _i + 2/\beta _i|^{1/4} \ll 1$). Finally, along a ‘critical line’ in the
$k_{\|} \rho _i \sim |\varDelta _i + 2/\beta _i|^{1/4} \ll 1$). Finally, along a ‘critical line’ in the ![]() $(k_{\|},k_{\perp })$ plane (
$(k_{\|},k_{\perp })$ plane (![]() $k_{\perp } \approx \sqrt {2/3} k_{\|}$,
$k_{\perp } \approx \sqrt {2/3} k_{\|}$, ![]() $\theta \approx 39^{\circ }$), the FLR coupling between the slow mode and shear-Alfvén wave becomes anomalously weak due to two opposing FLR effects cancelling each other out. This results in much weaker collisionless damping on critical-line firehose modes, and so they can exist on scales that are close to (though, as we prove here for the first time, not strictly at) the ion-Larmor scale. Thus critical-line firehose modes are generically the fastest-growing ones in high-
$\theta \approx 39^{\circ }$), the FLR coupling between the slow mode and shear-Alfvén wave becomes anomalously weak due to two opposing FLR effects cancelling each other out. This results in much weaker collisionless damping on critical-line firehose modes, and so they can exist on scales that are close to (though, as we prove here for the first time, not strictly at) the ion-Larmor scale. Thus critical-line firehose modes are generically the fastest-growing ones in high-![]() $\beta$ plasma (Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005).
$\beta$ plasma (Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005).
We support this claim with figure 19, which shows the maximum growth rate of the firehose-unstable modes as a function of both ![]() $k_{\|}$ and
$k_{\|}$ and ![]() $k_{\perp }$ for two different (unstable) values of
$k_{\perp }$ for two different (unstable) values of ![]() $\varDelta _i \beta _i$ (and with the same value of
$\varDelta _i \beta _i$ (and with the same value of ![]() $\beta _i$ as was used to calculate the stability maps presented in § 4.2). Both examples confirm that, although a broad spectrum of unstable parallel and oblique firehose modes emerge when
$\beta _i$ as was used to calculate the stability maps presented in § 4.2). Both examples confirm that, although a broad spectrum of unstable parallel and oblique firehose modes emerge when ![]() $\varDelta _i \beta _i +2 \lesssim -1$, it is the critical-line firehose modes that are the fastest growing.
$\varDelta _i \beta _i +2 \lesssim -1$, it is the critical-line firehose modes that are the fastest growing.

Figure 19. The CES firehose instability when ![]() $\varDelta _i \beta _i+2 \lesssim -1$. Maximum positive growth rates of linear perturbations resulting from the CE ion-shear term in the CE distribution function (4.1) with
$\varDelta _i \beta _i+2 \lesssim -1$. Maximum positive growth rates of linear perturbations resulting from the CE ion-shear term in the CE distribution function (4.1) with ![]() $\varDelta _i$ negative enough to surpass the long-wavelength firehose-instability threshold
$\varDelta _i$ negative enough to surpass the long-wavelength firehose-instability threshold ![]() $\varDelta _i = -2/\beta _i$ by at least an order-unity factor. The growth rates of all modes are calculated using the approach outlined in Appendix K.3. The growth rates are calculated on a
$\varDelta _i = -2/\beta _i$ by at least an order-unity factor. The growth rates of all modes are calculated using the approach outlined in Appendix K.3. The growth rates are calculated on a ![]() $400^2$ grid, with logarithmic spacing in both perpendicular and parallel directions between wavenumbers. The resulting growth rates, when normalised as
$400^2$ grid, with logarithmic spacing in both perpendicular and parallel directions between wavenumbers. The resulting growth rates, when normalised as ![]() $\gamma \beta _i/\varOmega _i$, are functions of two dimensionless parameters only:
$\gamma \beta _i/\varOmega _i$, are functions of two dimensionless parameters only: ![]() $\varDelta _i$ and
$\varDelta _i$ and ![]() $\beta _i$. The dashed white lines indicate the analytical predictions (4.67) for the parallel/perpendicular wavenumber at which peak growth is achieved, while the dotted line indicates the critical line
$\beta _i$. The dashed white lines indicate the analytical predictions (4.67) for the parallel/perpendicular wavenumber at which peak growth is achieved, while the dotted line indicates the critical line ![]() $k_{\perp } = k_{\|} \sqrt {2/3}$ along which the firehose growth rate is predicted to be maximal; (a)
$k_{\perp } = k_{\|} \sqrt {2/3}$ along which the firehose growth rate is predicted to be maximal; (a) ![]() $\varDelta _i \beta _i = -3$, (b)
$\varDelta _i \beta _i = -3$, (b) ![]() $\varDelta _i \beta _i = -30$. In both cases,
$\varDelta _i \beta _i = -30$. In both cases, ![]() $\beta _i = 10^{4}$.
$\beta _i = 10^{4}$.
The value of ![]() $\varDelta _i$ required to trigger the CES firehose instability is, as with the case of the firehose instability in a plasma with a bi-Maxwellian ion distribution, dependent on the scale of the unstable firehose modes. For long-wavelength firehose modes (i.e. those with
$\varDelta _i$ required to trigger the CES firehose instability is, as with the case of the firehose instability in a plasma with a bi-Maxwellian ion distribution, dependent on the scale of the unstable firehose modes. For long-wavelength firehose modes (i.e. those with ![]() $k \rho _i \ll 1$), the threshold is
$k \rho _i \ll 1$), the threshold is ![]() $\varDelta _i < (\varDelta _i)_{\rm c} = -2/\beta _i$; it can be shown that this result is independent of the particular form of the ion distribution function (Schekochihin et al. Reference Schekochihin, Cowley, Rincon and Rosin2010). However, our numerical solutions for the wavenumber-dependent growth rate of firehose modes in CE plasma when
$\varDelta _i < (\varDelta _i)_{\rm c} = -2/\beta _i$; it can be shown that this result is independent of the particular form of the ion distribution function (Schekochihin et al. Reference Schekochihin, Cowley, Rincon and Rosin2010). However, our numerical solutions for the wavenumber-dependent growth rate of firehose modes in CE plasma when ![]() $\varDelta _i > -2/\beta _i$ (see figure 20a) suggest that oblique ion-Larmor-scale firehose modes can be destabilised at less negative pressure anisotropies. This is consistent with the findings of previous studies of the oblique firehose in
$\varDelta _i > -2/\beta _i$ (see figure 20a) suggest that oblique ion-Larmor-scale firehose modes can be destabilised at less negative pressure anisotropies. This is consistent with the findings of previous studies of the oblique firehose in ![]() $\beta \sim 1$ plasma (Hellinger & Matsumoto Reference Hellinger and Matsumoto2000; Hellinger & Trávníček Reference Hellinger and Trávníček2008; Astfalk & Jenko Reference Astfalk and Jenko2016), although this finding has not until now been comprehensively studied in plasma with
$\beta \sim 1$ plasma (Hellinger & Matsumoto Reference Hellinger and Matsumoto2000; Hellinger & Trávníček Reference Hellinger and Trávníček2008; Astfalk & Jenko Reference Astfalk and Jenko2016), although this finding has not until now been comprehensively studied in plasma with ![]() $\beta \gg 1$. We can, in fact, calculate the threshold semi-analytically for the CES firehose instability as a function of wavenumber (see Appendix K.2.2); the results, which are shown in figure 20(b) show that oblique firehose modes with
$\beta \gg 1$. We can, in fact, calculate the threshold semi-analytically for the CES firehose instability as a function of wavenumber (see Appendix K.2.2); the results, which are shown in figure 20(b) show that oblique firehose modes with ![]() $k_{\|} \rho _i \approx 0.45$,
$k_{\|} \rho _i \approx 0.45$, ![]() $k_{\perp } \rho _i \approx 0.3$ become unstable when
$k_{\perp } \rho _i \approx 0.3$ become unstable when ![]() $\varDelta _i \approx -1.35/\beta _i$. The reduced threshold of ion-Larmor-scale firehose modes, which can be shown to depend only on fourth- and higher-order moments of the ion distribution function, is considered in greater depth in Bott et al. (2023, in prep.).
$\varDelta _i \approx -1.35/\beta _i$. The reduced threshold of ion-Larmor-scale firehose modes, which can be shown to depend only on fourth- and higher-order moments of the ion distribution function, is considered in greater depth in Bott et al. (2023, in prep.).

Figure 20. Onset of the CES firehose instability. (a) Maximum positive growth rates of linear perturbations resulting from the CE ion-shear term in the CE distribution function (4.1) with ![]() $\beta _i = 10^{4}$ and
$\beta _i = 10^{4}$ and ![]() $\varDelta _i = -1.7/\beta _i$ (a value at which the long-wavelength firehose instability is absent, because
$\varDelta _i = -1.7/\beta _i$ (a value at which the long-wavelength firehose instability is absent, because ![]() $\varDelta _i > -2/\beta _i$). The growth rates of all modes are calculated in the same way as figure 19. (b) Threshold value
$\varDelta _i > -2/\beta _i$). The growth rates of all modes are calculated in the same way as figure 19. (b) Threshold value ![]() $(\varDelta _i \beta _i)_{c}$ of
$(\varDelta _i \beta _i)_{c}$ of ![]() $\varDelta _i \beta _i$ at which modes with parallel and perpendicular wavenumber
$\varDelta _i \beta _i$ at which modes with parallel and perpendicular wavenumber ![]() $k_{\|}$ and
$k_{\|}$ and ![]() $k_{\perp }$, respectively, become firehose unstable. Regions of
$k_{\perp }$, respectively, become firehose unstable. Regions of ![]() $(k_{\|},k_{\perp })$ that are shaded black are stable.
$(k_{\|},k_{\perp })$ that are shaded black are stable.
The growth of the three different sub-categories of unstable CES firehose modes (quasi-parallel, oblique and critical-line firehoses) can be described analytically. However, the relative orderings of ![]() $\tilde {\omega }_{i\|}$,
$\tilde {\omega }_{i\|}$, ![]() $k_{\|} \rho _i$,
$k_{\|} \rho _i$, ![]() $k_{\bot } \rho _i$,
$k_{\bot } \rho _i$, ![]() $\beta _i$ and
$\beta _i$ and ![]() $|\varDelta _i|$ for these sub-categories are different, so it is necessary to treat them separately.
$|\varDelta _i|$ for these sub-categories are different, so it is necessary to treat them separately.
4.4.2. Quasi-parallel firehose instability
The relevant orderings of parameters for quasi-parallel firehose modes is
with the additional small wavenumber-angle condition
Under the ordering (4.45), we find (see Appendix K.3.6) that there are four modes with complex frequencies given by
 \begin{equation} \frac{\omega}{\varOmega_i} ={\pm} k_{\|} \rho_i \left(\frac{1}{4} k_{\|} \rho_i \pm \sqrt{\frac{1}{16} k_{\|}^2 \rho_i^2 + \frac{1}{\beta_i}+\frac{\varDelta_i}{2}} \right) , \end{equation}
\begin{equation} \frac{\omega}{\varOmega_i} ={\pm} k_{\|} \rho_i \left(\frac{1}{4} k_{\|} \rho_i \pm \sqrt{\frac{1}{16} k_{\|}^2 \rho_i^2 + \frac{1}{\beta_i}+\frac{\varDelta_i}{2}} \right) , \end{equation}
where the ![]() $\pm$ signs can be chosen independently. This is the standard parallel firehose dispersion relation (Kennel & Sagdeev Reference Kennel and Sagdeev1967; Davidson & Völk Reference Davidson and Völk1968; Schekochihin et al. Reference Schekochihin, Cowley, Rincon and Rosin2010). To (re-)identify the modes that are destabilised by the negative ion-pressure anisotropy, we set
$\pm$ signs can be chosen independently. This is the standard parallel firehose dispersion relation (Kennel & Sagdeev Reference Kennel and Sagdeev1967; Davidson & Völk Reference Davidson and Völk1968; Schekochihin et al. Reference Schekochihin, Cowley, Rincon and Rosin2010). To (re-)identify the modes that are destabilised by the negative ion-pressure anisotropy, we set ![]() $\varDelta _i = 0$: the resulting dispersion relation agrees with Foote & Kulsrud (Reference Foote and Kulsrud1979), recovering the dispersion relation of Alfvén waves in the limit
$\varDelta _i = 0$: the resulting dispersion relation agrees with Foote & Kulsrud (Reference Foote and Kulsrud1979), recovering the dispersion relation of Alfvén waves in the limit ![]() $k_\| \rho _i \ll \beta _i^{-1/2}$ (see their (19)) and the dispersion relation of the slow and fast hydromagnetic waves in the limit
$k_\| \rho _i \ll \beta _i^{-1/2}$ (see their (19)) and the dispersion relation of the slow and fast hydromagnetic waves in the limit ![]() $k_\| \rho _i \gg \beta _i^{-1/2}$ (see their (20)). The growth rate of the unstable parallel firehose modes that follows from (4.47) is shown in figure 21 for several different values of
$k_\| \rho _i \gg \beta _i^{-1/2}$ (see their (20)). The growth rate of the unstable parallel firehose modes that follows from (4.47) is shown in figure 21 for several different values of ![]() $\varDelta _i$ and
$\varDelta _i$ and ![]() $\beta _i$; the results closely match the analogous result determined numerically.Footnote 6
$\beta _i$; the results closely match the analogous result determined numerically.Footnote 6

Figure 21. Parallel CES firehose instability. Growth rates of Alfvén waves whose instability is driven by the CE ion-shear term in the CE distribution function (4.1), for wavevectors co-parallel with the background magnetic field (viz. ![]() $\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The growth rates (solid lines) of all modes are calculated in the same way as figure 19. We show the growth rates for a selection of different values of
$\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The growth rates (solid lines) of all modes are calculated in the same way as figure 19. We show the growth rates for a selection of different values of ![]() $\varDelta _i \beta _i$ and
$\varDelta _i \beta _i$ and ![]() $\beta _i$. The approximation (4.47) for the growth rate (dashed red) in the limit
$\beta _i$. The approximation (4.47) for the growth rate (dashed red) in the limit ![]() $k_{\|} \rho _i \ll 1$ is also plotted.
$k_{\|} \rho _i \ll 1$ is also plotted.
For non-zero ![]() $\varDelta _i$ and fixed
$\varDelta _i$ and fixed ![]() $k_\| \rho _i$, (4.47) implies that we have instability provided
$k_\| \rho _i$, (4.47) implies that we have instability provided
The fastest-growing mode
occurs at the characteristic wavenumber
 \begin{equation} (k_\| \rho_i)_{\mathrm{peak}} = 2 \left|\frac{2}{\beta_i}+\varDelta_i\right|^{1/2} . \end{equation}
\begin{equation} (k_\| \rho_i)_{\mathrm{peak}} = 2 \left|\frac{2}{\beta_i}+\varDelta_i\right|^{1/2} . \end{equation}
For ![]() $k_\| \rho _i > 2 \sqrt {2} |2 \beta _i^{-1}+\varDelta _i|^{1/2}$, the unstable mode is stabilised. This agrees with previous analytical characterisations of the firehose instability (Rosin et al. Reference Rosin, Schekochihin, Rincon and Cowley2011).
$k_\| \rho _i > 2 \sqrt {2} |2 \beta _i^{-1}+\varDelta _i|^{1/2}$, the unstable mode is stabilised. This agrees with previous analytical characterisations of the firehose instability (Rosin et al. Reference Rosin, Schekochihin, Rincon and Cowley2011).
4.4.3. Oblique firehose instability
In this case, we order
Aside from the finite propagation angle of oblique modes, the key difference between the oblique and quasiparallel cases is the larger magnitude of the typical wavenumber ![]() $k \rho _i \sim \beta _i^{-1/4}$. The unstable oblique firehose modes have the complex frequency (see Appendix K.3.7)
$k \rho _i \sim \beta _i^{-1/4}$. The unstable oblique firehose modes have the complex frequency (see Appendix K.3.7)
 \begin{align} \frac{\omega}{\varOmega_i} & ={-}k_{\|} \rho_i \left[\frac{\mathrm{i}}{8 \sqrt{\rm \pi} k_{\bot}^2 \rho_i^2} \left(k_{\|}^2 \rho_i^2 - \frac{3}{2} k_{\bot}^2 \rho_i^2 \right)^2\right. \nonumber\\ & \quad \left.\pm \sqrt{\frac{1}{\beta_i}+\frac{\varDelta_i}{2} - \frac{1}{64 {\rm \pi}k_{\bot}^4 \rho_i^4} \left(k_{\|}^2 \rho_i^2 - \frac{3}{2} k_{\bot}^2 \rho_i^2 \right)^4} \right] . \end{align}
\begin{align} \frac{\omega}{\varOmega_i} & ={-}k_{\|} \rho_i \left[\frac{\mathrm{i}}{8 \sqrt{\rm \pi} k_{\bot}^2 \rho_i^2} \left(k_{\|}^2 \rho_i^2 - \frac{3}{2} k_{\bot}^2 \rho_i^2 \right)^2\right. \nonumber\\ & \quad \left.\pm \sqrt{\frac{1}{\beta_i}+\frac{\varDelta_i}{2} - \frac{1}{64 {\rm \pi}k_{\bot}^4 \rho_i^4} \left(k_{\|}^2 \rho_i^2 - \frac{3}{2} k_{\bot}^2 \rho_i^2 \right)^4} \right] . \end{align}
Setting ![]() $|\varDelta _i| = 0$, and considering the subsidiary limit
$|\varDelta _i| = 0$, and considering the subsidiary limit ![]() $k \rho _i \ll \beta _i^{-1/4}$, we recover the dispersion relation of the shear-Alfvén mode (Foote & Kulsrud Reference Foote and Kulsrud1979).
$k \rho _i \ll \beta _i^{-1/4}$, we recover the dispersion relation of the shear-Alfvén mode (Foote & Kulsrud Reference Foote and Kulsrud1979).
Similarly to the quasi-parallel firehose instability, the instability condition is still
If this condition is met, the maximum growth rate of the instability is
 \begin{equation} \frac{\gamma_{\mathrm{max}}}{\varOmega_i} \approx \left(\frac{8 {\rm \pi}}{27}\right)^{1/4} \left|\frac{2}{\beta_i}+\varDelta_i\right|^{3/4} \tan{\theta} \left[1-\frac{3}{2} \tan^2{\theta}\right]^{{-}1} , \end{equation}
\begin{equation} \frac{\gamma_{\mathrm{max}}}{\varOmega_i} \approx \left(\frac{8 {\rm \pi}}{27}\right)^{1/4} \left|\frac{2}{\beta_i}+\varDelta_i\right|^{3/4} \tan{\theta} \left[1-\frac{3}{2} \tan^2{\theta}\right]^{{-}1} , \end{equation}and is attained at (parallel) wavenumber
 \begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} \approx \left(\frac{32 {\rm \pi}}{3}\right)^{1/4} \left|\frac{2}{\beta_i}+\varDelta_i\right|^{1/4} \tan{\theta} \left[1-\frac{3}{2} \tan^2{\theta} \right]^{{-}1} , \end{equation}
\begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} \approx \left(\frac{32 {\rm \pi}}{3}\right)^{1/4} \left|\frac{2}{\beta_i}+\varDelta_i\right|^{1/4} \tan{\theta} \left[1-\frac{3}{2} \tan^2{\theta} \right]^{{-}1} , \end{equation}
where ![]() $\theta = \tan ^{-1}(k_{\perp }/k_\|)$ is (again) the wavevector angle with respect to the magnetic field. In contrast to the quasi-parallel case, if the condition (4.53) is met, the instability persists for all wavenumbers satisfying
$\theta = \tan ^{-1}(k_{\perp }/k_\|)$ is (again) the wavevector angle with respect to the magnetic field. In contrast to the quasi-parallel case, if the condition (4.53) is met, the instability persists for all wavenumbers satisfying ![]() $k \rho _i \lesssim 1$, albeit with a decreasing growth rate beyond the parallel wavenumber given by (4.55). We notice that along the critical line
$k \rho _i \lesssim 1$, albeit with a decreasing growth rate beyond the parallel wavenumber given by (4.55). We notice that along the critical line ![]() $k_{\bot } = k_{\|}\sqrt {2/3}$ (
$k_{\bot } = k_{\|}\sqrt {2/3}$ (![]() $\theta \approx 39^{\circ }$), the maximum growth rate (4.54) of the oblique firehose diverges. This divergence is mathematically the result of failing to take into account higher-order terms in the
$\theta \approx 39^{\circ }$), the maximum growth rate (4.54) of the oblique firehose diverges. This divergence is mathematically the result of failing to take into account higher-order terms in the ![]() $k \rho _i \ll 1$ expansion, but, as was discussed earlier in this section, it is indicative of a physical effect (viz. much faster growth of firehose modes with
$k \rho _i \ll 1$ expansion, but, as was discussed earlier in this section, it is indicative of a physical effect (viz. much faster growth of firehose modes with ![]() $k_{\bot } = k_{\|}\sqrt {2/3}$).
$k_{\bot } = k_{\|}\sqrt {2/3}$).
The degree to which the growth rate of unstable modes determined from (4.52) follows a numerical solution for a particular choice of ![]() $\theta$ is demonstrated in figure 22. The agreement is reasonable, although an increasingly large discrepancy develops as
$\theta$ is demonstrated in figure 22. The agreement is reasonable, although an increasingly large discrepancy develops as ![]() $k \rho _i$ approaches unity due to FLR effects.
$k \rho _i$ approaches unity due to FLR effects.

Figure 22. Oblique CES firehose instability. Growth rates of the shear-Alfvén mode whose instability is driven by the CE ion-shear term in the CE distribution function (4.1), for wavevectors at an angle ![]() $\theta = 60^{\circ }$ with the background magnetic field (viz.
$\theta = 60^{\circ }$ with the background magnetic field (viz. ![]() $k_{\perp } = \sqrt {3} k_{\|}$). The growth rates (solid lines) of all modes are calculated in the same way as figure 19. We show the growth rates for a selection of different values of
$k_{\perp } = \sqrt {3} k_{\|}$). The growth rates (solid lines) of all modes are calculated in the same way as figure 19. We show the growth rates for a selection of different values of ![]() $\varDelta _i \beta _i$ and
$\varDelta _i \beta _i$ and ![]() $\beta _i$. The approximation (4.52) for the growth rate (dashed red) in the limit
$\beta _i$. The approximation (4.52) for the growth rate (dashed red) in the limit ![]() $k_{\|} \rho _i \ll 1$ is also plotted.
$k_{\|} \rho _i \ll 1$ is also plotted.
4.4.4. Critical-line firehose instability
In this third and final case, we set ![]() $k_{\bot } = k_{\|} \sqrt {2/3}$. The FLR coupling between the shear-Alfvén mode and the Barnes’-damped slow-mode then vanishes to leading order in
$k_{\bot } = k_{\|} \sqrt {2/3}$. The FLR coupling between the shear-Alfvén mode and the Barnes’-damped slow-mode then vanishes to leading order in ![]() $k \rho _i \ll 1$, and next-order FLR terms must be considered. Depending on the value of
$k \rho _i \ll 1$, and next-order FLR terms must be considered. Depending on the value of ![]() $\beta _i$, we find two sub-cases.
$\beta _i$, we find two sub-cases.
First, for ![]() $\beta _i \sim \varDelta _i^{-1} \gg 10^{6}$ – a numerical bound that we will justify a posteriori following our calculations – the FLR term responsible for setting the wavenumber of the fastest-growing mode is the second-order correction to the FLR coupling between the shear-Alfvén and slow modes. The appropriate ordering to adopt then depends on the relative magnitude of
$\beta _i \sim \varDelta _i^{-1} \gg 10^{6}$ – a numerical bound that we will justify a posteriori following our calculations – the FLR term responsible for setting the wavenumber of the fastest-growing mode is the second-order correction to the FLR coupling between the shear-Alfvén and slow modes. The appropriate ordering to adopt then depends on the relative magnitude of ![]() $\varDelta _i$ and
$\varDelta _i$ and ![]() $\beta _{i}^{-1}$. For
$\beta _{i}^{-1}$. For ![]() $\varDelta _i \beta _i + 2 \lesssim -1$, we use the ordering
$\varDelta _i \beta _i + 2 \lesssim -1$, we use the ordering
In this case, we find (see Appendix K.3.8) that the frequency of the two shear-Alfvén modes is given by
 \begin{equation} \frac{\omega}{\varOmega_i} ={-}k_{\|} \rho_i \left[\frac{ 6889 \mathrm{i} k_{\|}^6 \rho_i^6}{27\,648 \sqrt{\rm \pi}} \pm \sqrt{\left(\frac{1}{\beta_i}+\frac{\varDelta_i}{2}\right) - \frac{6889^2}{27\,648^2 {\rm \pi}} k_{\|}^{12} \rho_i^{12} } \right] . \end{equation}
\begin{equation} \frac{\omega}{\varOmega_i} ={-}k_{\|} \rho_i \left[\frac{ 6889 \mathrm{i} k_{\|}^6 \rho_i^6}{27\,648 \sqrt{\rm \pi}} \pm \sqrt{\left(\frac{1}{\beta_i}+\frac{\varDelta_i}{2}\right) - \frac{6889^2}{27\,648^2 {\rm \pi}} k_{\|}^{12} \rho_i^{12} } \right] . \end{equation}
The wavelength at which the growth rate is maximised scales with an extraordinarily low power of ![]() $|2\beta _i^{-1}+\varDelta _i|$:
$|2\beta _i^{-1}+\varDelta _i|$:
 \begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} \approx \frac{2^{19/12} 3^{1/2}{\rm \pi}^{1/12}}{83^{1/3} 35^{1/12}} \left|\frac{2}{\beta_i}+\varDelta_i\right|^{1/12} \approx 0.97 \left|\frac{2}{\beta_i}+\varDelta_i\right|^{1/12} , \end{equation}
\begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} \approx \frac{2^{19/12} 3^{1/2}{\rm \pi}^{1/12}}{83^{1/3} 35^{1/12}} \left|\frac{2}{\beta_i}+\varDelta_i\right|^{1/12} \approx 0.97 \left|\frac{2}{\beta_i}+\varDelta_i\right|^{1/12} , \end{equation}with associated maximum growth rate
 \begin{equation} \frac{\gamma_{\mathrm{max}}}{\varOmega_i} \approx \frac{2^{13/12} 3^{1/2}{\rm \pi}^{1/12}}{83^{1/3} 35^{1/12}} \left|\frac{2}{\beta_i}+\varDelta_i\right|^{7/12} \approx 0.58 \left|\frac{2}{\beta_i}+\varDelta_i\right|^{7/12} . \end{equation}
\begin{equation} \frac{\gamma_{\mathrm{max}}}{\varOmega_i} \approx \frac{2^{13/12} 3^{1/2}{\rm \pi}^{1/12}}{83^{1/3} 35^{1/12}} \left|\frac{2}{\beta_i}+\varDelta_i\right|^{7/12} \approx 0.58 \left|\frac{2}{\beta_i}+\varDelta_i\right|^{7/12} . \end{equation} As discussed in § 4.4.1, the instability threshold for critical-line firehose modes is not (4.53), but is a less stringent value. We can demonstrate this analytically by showing that, for ![]() $\varDelta _i \simeq -2/\beta _i$, critical-line firehose modes are still unstable. Adopting the ordering
$\varDelta _i \simeq -2/\beta _i$, critical-line firehose modes are still unstable. Adopting the ordering
it follows (see Appendix K.3.8) that the growth rate of the critical-line firehose modes is
 \begin{equation} \frac{\gamma}{\varOmega_i} ={-}k_{\|} \rho_i \left[\frac{ 6889 k_{\|}^6 \rho_i^6}{27\,648 \sqrt{\rm \pi}} \pm \sqrt{\frac{5}{4 \beta_i} k_{\|}^2 \rho_i^2 + \frac{6889^2}{27\,648^2 {\rm \pi}} k_{\|}^{12} \rho_i^{12} } \right] . \end{equation}
\begin{equation} \frac{\gamma}{\varOmega_i} ={-}k_{\|} \rho_i \left[\frac{ 6889 k_{\|}^6 \rho_i^6}{27\,648 \sqrt{\rm \pi}} \pm \sqrt{\frac{5}{4 \beta_i} k_{\|}^2 \rho_i^2 + \frac{6889^2}{27\,648^2 {\rm \pi}} k_{\|}^{12} \rho_i^{12} } \right] . \end{equation}The maximum growth rate of such modes is then given by
obtained at parallel wavenumber
When ![]() $\beta _i \sim \varDelta _i^{-1} \ll 10^{6}$ the fastest-growing critical-line firehose modes have a sufficiently large wavenumber that the effect of FLR coupling between shear-Alfvén and slow modes is sub-dominant to the effect of cyclotron damping. Assuming that
$\beta _i \sim \varDelta _i^{-1} \ll 10^{6}$ the fastest-growing critical-line firehose modes have a sufficiently large wavenumber that the effect of FLR coupling between shear-Alfvén and slow modes is sub-dominant to the effect of cyclotron damping. Assuming that ![]() $\varDelta _i \beta _i + 2 \lesssim -1$ and adopting the ordering
$\varDelta _i \beta _i + 2 \lesssim -1$ and adopting the ordering
 \begin{equation} \tilde{\omega}_{i\|} \sim \frac{1}{\beta_i^{1/2}} \sim |\varDelta_i|^{1/2} , \quad k_{\|} \rho_i \sim \frac{1}{\sqrt{\log{1/\left|\beta_i^{{-}1}+\varDelta_i/2\right|}}} , \end{equation}
\begin{equation} \tilde{\omega}_{i\|} \sim \frac{1}{\beta_i^{1/2}} \sim |\varDelta_i|^{1/2} , \quad k_{\|} \rho_i \sim \frac{1}{\sqrt{\log{1/\left|\beta_i^{{-}1}+\varDelta_i/2\right|}}} , \end{equation}we show in Appendix K.3.8 that the frequency of the shear-Alfvén modes becomes
 \begin{equation} \frac{\omega}{\varOmega_i} ={-} \frac{\mathrm{i} \sqrt{\rm \pi}}{2 k_{\|} \rho_i} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} \pm k_{\|} \rho_i \sqrt{\left(\frac{1}{\beta_i}+\frac{\varDelta_i}{2}\right) - \frac{\rm \pi}{4 k_{\|}^4 \rho_i^4} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} } . \end{equation}
\begin{equation} \frac{\omega}{\varOmega_i} ={-} \frac{\mathrm{i} \sqrt{\rm \pi}}{2 k_{\|} \rho_i} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} \pm k_{\|} \rho_i \sqrt{\left(\frac{1}{\beta_i}+\frac{\varDelta_i}{2}\right) - \frac{\rm \pi}{4 k_{\|}^4 \rho_i^4} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} } . \end{equation}In this case, the maximum growth rate
 \begin{equation} \frac{\gamma_{\mathrm{max}}}{\varOmega_i} \approx (k_{\|} \rho_i)_{\mathrm{peak}} \left|\frac{1}{\beta_i}+\frac{\varDelta_i}{2}\right|^{1/2} ,\end{equation}
\begin{equation} \frac{\gamma_{\mathrm{max}}}{\varOmega_i} \approx (k_{\|} \rho_i)_{\mathrm{peak}} \left|\frac{1}{\beta_i}+\frac{\varDelta_i}{2}\right|^{1/2} ,\end{equation}is attained at
 \begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} \approx \frac{\sqrt{2}}{\sqrt{\log{1/\left|\beta_i^{{-}1}+\varDelta_i/2\right|}}} \left[1-\frac{4 \log{\left(\log{1/\sqrt{\left|\beta_i^{{-}1}+\varDelta_i/2\right|}}\right)}}{\log{1/\left|\beta_i^{{-}1}+\varDelta_i/2\right|}}\right] . \end{equation}
\begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} \approx \frac{\sqrt{2}}{\sqrt{\log{1/\left|\beta_i^{{-}1}+\varDelta_i/2\right|}}} \left[1-\frac{4 \log{\left(\log{1/\sqrt{\left|\beta_i^{{-}1}+\varDelta_i/2\right|}}\right)}}{\log{1/\left|\beta_i^{{-}1}+\varDelta_i/2\right|}}\right] . \end{equation}Figure 19 corroborates that the analytical approximation (4.67) provides a reasonable estimate of the parallel wavenumber at which peak growth occurs.
Similarly to the ![]() $\beta _i \gg 10^{6}$ regime, when
$\beta _i \gg 10^{6}$ regime, when ![]() $\beta _i \ll 10^{6}$, critical-line firehose modes still grow when
$\beta _i \ll 10^{6}$, critical-line firehose modes still grow when ![]() $\varDelta _i \approx -2/\beta _i$. Their growth rate as a function of wavenumber is given by
$\varDelta _i \approx -2/\beta _i$. Their growth rate as a function of wavenumber is given by
 \begin{equation} \frac{\gamma}{\varOmega_i} ={-} \frac{\sqrt{\rm \pi}}{2 k_{\|} \rho_i} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} \pm k_{\|} \rho_i \sqrt{\frac{5}{4 \beta_i} k_{\|}^2 \rho_i^2 + \frac{\rm \pi}{4 k_{\|}^4 \rho_i^4} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} } . \end{equation}
\begin{equation} \frac{\gamma}{\varOmega_i} ={-} \frac{\sqrt{\rm \pi}}{2 k_{\|} \rho_i} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} \pm k_{\|} \rho_i \sqrt{\frac{5}{4 \beta_i} k_{\|}^2 \rho_i^2 + \frac{\rm \pi}{4 k_{\|}^4 \rho_i^4} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} } . \end{equation}The maximum of (4.68),
is achieved at
 \begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} \approx \frac{\sqrt{2}}{\sqrt{\log{\left({\rm \pi} \beta_i/20\right)}}} \left\{1 - \frac{3\log{\left[\log{\left({\rm \pi} \beta_i/20\right)}/2\right]}}{\log{\left({\rm \pi} \beta_i/20\right)}}\right\} . \end{equation}
\begin{equation} (k_{\|} \rho_i)_{\mathrm{peak}} \approx \frac{\sqrt{2}}{\sqrt{\log{\left({\rm \pi} \beta_i/20\right)}}} \left\{1 - \frac{3\log{\left[\log{\left({\rm \pi} \beta_i/20\right)}/2\right]}}{\log{\left({\rm \pi} \beta_i/20\right)}}\right\} . \end{equation} By comparing the expressions (4.57) and (4.65) for the complex frequency of shear-Alfvén modes – specifically, the ratio of the final terms – the dependence on ![]() $\beta _i$ (equivalently,
$\beta _i$ (equivalently, ![]() $\varDelta _i$) of the relative importance of FLR slow-mode coupling and cyclotron damping can be determined. This ratio is
$\varDelta _i$) of the relative importance of FLR slow-mode coupling and cyclotron damping can be determined. This ratio is ![]() ${\sim }0.16 k_{\|}^8 \rho _i^8 \exp {(-{1}/{k_\|^2 \rho _i^2})}$, with equality being achieved when
${\sim }0.16 k_{\|}^8 \rho _i^8 \exp {(-{1}/{k_\|^2 \rho _i^2})}$, with equality being achieved when ![]() $k_{\|} \rho _i \approx 0.3$. Using (4.58) to estimating the value of
$k_{\|} \rho _i \approx 0.3$. Using (4.58) to estimating the value of ![]() $|2\beta _i^{-1}+\varDelta _i|$ at which this value of
$|2\beta _i^{-1}+\varDelta _i|$ at which this value of ![]() $k_\| \rho _i$ is achieved, we find that
$k_\| \rho _i$ is achieved, we find that ![]() $|2\beta _i^{-1}+\varDelta _i| \approx 8 \times 10^{-7}$. Assuming
$|2\beta _i^{-1}+\varDelta _i| \approx 8 \times 10^{-7}$. Assuming ![]() $|\varDelta _i \beta _i^{-1} + 2| \sim 1$, we conclude that, for
$|\varDelta _i \beta _i^{-1} + 2| \sim 1$, we conclude that, for ![]() $\beta _i \lesssim 10^{6}$, cyclotron damping will determine the wavenumber cutoff, with this transition value of
$\beta _i \lesssim 10^{6}$, cyclotron damping will determine the wavenumber cutoff, with this transition value of ![]() $\beta _i$ proportional to the value of
$\beta _i$ proportional to the value of ![]() $|\varDelta _i| \beta _i$. This estimate can be validated numerically by comparing (4.57) and (4.65) with the numerically determined growth rate (see figure 23). We indeed find that, for
$|\varDelta _i| \beta _i$. This estimate can be validated numerically by comparing (4.57) and (4.65) with the numerically determined growth rate (see figure 23). We indeed find that, for ![]() $\beta _i \sim \varDelta _i^{-1} \ll 10^6$, the effect of cyclotron damping sets the wavenumber of peak growth, while FLR slow-mode coupling does so for
$\beta _i \sim \varDelta _i^{-1} \ll 10^6$, the effect of cyclotron damping sets the wavenumber of peak growth, while FLR slow-mode coupling does so for ![]() $\beta _i \sim \varDelta _i^{-1} \gg 10^6$. In both cases, the superior of the two analytic approximations closely matches the numerical growth rate.
$\beta _i \sim \varDelta _i^{-1} \gg 10^6$. In both cases, the superior of the two analytic approximations closely matches the numerical growth rate.

Figure 23. Critical-line CES firehose instability. Growth rates of shear-Alfvén modes whose instability is driven by the CE ion-shear term in the CE distribution function (4.1), for wavevectors at an angle ![]() $\theta \approx 39^{\circ }$ with the background magnetic field (viz.
$\theta \approx 39^{\circ }$ with the background magnetic field (viz. ![]() $k_{\perp } = \sqrt {2/3} k_{\|}$). The growth rates (solid lines) of all modes are calculated in the same way as figure 19. We show the growth rates for a selection of different values of
$k_{\perp } = \sqrt {2/3} k_{\|}$). The growth rates (solid lines) of all modes are calculated in the same way as figure 19. We show the growth rates for a selection of different values of ![]() $\varDelta _i \beta _i$ and
$\varDelta _i \beta _i$ and ![]() $\beta _i$. The approximations (4.57) and (4.65) for the growth rate (dashed and dotted red, respectively) in the limit
$\beta _i$. The approximations (4.57) and (4.65) for the growth rate (dashed and dotted red, respectively) in the limit ![]() $k_{\|} \rho _i \ll 1$ are also plotted.
$k_{\|} \rho _i \ll 1$ are also plotted.
These results suggest that, for very large ![]() $\beta _i$, the wavenumber of the maximum growth of the firehose instability satisfies
$\beta _i$, the wavenumber of the maximum growth of the firehose instability satisfies ![]() $k \rho _i \ll 1$, rather than
$k \rho _i \ll 1$, rather than ![]() $k \rho _i \sim 1$. This result might seem to contradict previous authors who claim to have found numerical evidence that the fastest growth rates of the firehose instability occur at
$k \rho _i \sim 1$. This result might seem to contradict previous authors who claim to have found numerical evidence that the fastest growth rates of the firehose instability occur at ![]() $k \rho _i \sim 1$ (Yoon et al. Reference Yoon, Wu and de Assis1993; Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005; Kunz et al. Reference Kunz, Schekochihin and Stone2014); however, given the logarithmic dependence of the characteristic wavenumber (4.67), we conclude that it would take simulations at very high
$k \rho _i \sim 1$ (Yoon et al. Reference Yoon, Wu and de Assis1993; Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005; Kunz et al. Reference Kunz, Schekochihin and Stone2014); however, given the logarithmic dependence of the characteristic wavenumber (4.67), we conclude that it would take simulations at very high ![]() $\beta _i$ to be able to distinguish between
$\beta _i$ to be able to distinguish between ![]() $k \rho _i \sim 1$ and
$k \rho _i \sim 1$ and ![]() $k \rho _i \sim \beta _i^{-1/12} \ll 1$. In addition, the results presented in figure 20(b) indicate that firehose modes with
$k \rho _i \sim \beta _i^{-1/12} \ll 1$. In addition, the results presented in figure 20(b) indicate that firehose modes with ![]() $k \rho _i \sim 1$ have a less stringent instability threshold on
$k \rho _i \sim 1$ have a less stringent instability threshold on ![]() $\varDelta _i$ than (4.53), providing an opportunity for such modes to grow significantly before longer-wavelength modes can do so. In short, it seems reasonable to assume for all practical purposes that the dominant firehose modes occur at
$\varDelta _i$ than (4.53), providing an opportunity for such modes to grow significantly before longer-wavelength modes can do so. In short, it seems reasonable to assume for all practical purposes that the dominant firehose modes occur at ![]() $k \rho _i \sim 1$, provided
$k \rho _i \sim 1$, provided ![]() $\beta _i$ is not extremely large.
$\beta _i$ is not extremely large.
4.4.5. Sub-ion-Larmor-scale firehose instability
Figure 19(b) also suggests that, once ![]() $|\varDelta _i| \beta _i \gg 1$, firehose modes on sub-ion-Larmor scales develop – albeit with a smaller growth rate than the critical-line ones. Similarly to sub-ion-Larmor-scale mirror modes (see the end of § 4.3.1), we can characterise these modes analytically by adopting the ordering
$|\varDelta _i| \beta _i \gg 1$, firehose modes on sub-ion-Larmor scales develop – albeit with a smaller growth rate than the critical-line ones. Similarly to sub-ion-Larmor-scale mirror modes (see the end of § 4.3.1), we can characterise these modes analytically by adopting the ordering
If we also assume that ![]() $|\varDelta _i| \beta _i \ll \mu _e^{-1/2}$, it is shown in Appendix K.3.2 that the growth rate of these modes is given by
$|\varDelta _i| \beta _i \ll \mu _e^{-1/2}$, it is shown in Appendix K.3.2 that the growth rate of these modes is given by
 \begin{align} \frac{\gamma}{\varOmega_i} & \approx \frac{k_\|}{k} \sqrt{\left(-\varDelta_i \frac{k_{\bot}^2-k_{\|}^2}{k^2} - \frac{k^2 \rho_i^2}{\beta_i} \right) \left(\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \frac{k_{\|}^2}{k^2}\right)} \nonumber\\ & = \cos{\theta} \sqrt{\left[-\varDelta_i \left(\sin^2{\theta}-\cos^2{\theta}\right)- \frac{k^2 \rho_i^2}{\beta_i} \right] \left(\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \cos^2{\theta} \right)} . \end{align}
\begin{align} \frac{\gamma}{\varOmega_i} & \approx \frac{k_\|}{k} \sqrt{\left(-\varDelta_i \frac{k_{\bot}^2-k_{\|}^2}{k^2} - \frac{k^2 \rho_i^2}{\beta_i} \right) \left(\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \frac{k_{\|}^2}{k^2}\right)} \nonumber\\ & = \cos{\theta} \sqrt{\left[-\varDelta_i \left(\sin^2{\theta}-\cos^2{\theta}\right)- \frac{k^2 \rho_i^2}{\beta_i} \right] \left(\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \cos^2{\theta} \right)} . \end{align}
If ![]() $\varDelta _i < 0$, we have an instability for all modes with
$\varDelta _i < 0$, we have an instability for all modes with ![]() $\theta > 45^{\circ }$ whose total wavenumber satisfies
$\theta > 45^{\circ }$ whose total wavenumber satisfies
Analogously to the sub-ion-Larmor-scale mirror modes (cf. (4.18)), the growth is maximised when ![]() $k \rho _i\ll (|\varDelta _i| \beta _i)^{1/2}$ and
$k \rho _i\ll (|\varDelta _i| \beta _i)^{1/2}$ and ![]() $\theta \approx 55^{\circ }$, with
$\theta \approx 55^{\circ }$, with
In contrast to the case of the mirror instability, this growth rate is asymptotically small in ![]() $\varDelta _i \ll 1$ compared with the peak growth rate of the critical-line firehose modes (cf. (4.59) and (4.67)), and thus the instability of sub-ion-Larmor-scale firehose modes is always subdominant. For completeness, we note that, once
$\varDelta _i \ll 1$ compared with the peak growth rate of the critical-line firehose modes (cf. (4.59) and (4.67)), and thus the instability of sub-ion-Larmor-scale firehose modes is always subdominant. For completeness, we note that, once ![]() $|\varDelta _i| \beta _i \sim \mu _e^{-1/2}$, the electron-pressure anisotropy associated with the CE electron-shear term begins to play a comparable role to the ion-pressure anisotropy for modes with
$|\varDelta _i| \beta _i \sim \mu _e^{-1/2}$, the electron-pressure anisotropy associated with the CE electron-shear term begins to play a comparable role to the ion-pressure anisotropy for modes with ![]() $k \rho _i \sim (|\varDelta _i| \beta _i)^{1/2}$. In this case, the expression for the growth rate becomes
$k \rho _i \sim (|\varDelta _i| \beta _i)^{1/2}$. In this case, the expression for the growth rate becomes
 \begin{align} \frac{\gamma}{\varOmega_i} & \approx \frac{k_\|}{k} \left\{\left[-\varDelta_i \frac{k_{\bot}^2-k_{\|}^2}{k^2} - k^2 \rho_i^2\left(\frac{1}{\beta_i} +\frac{\mu_e^{1/2} \varDelta_i}{2}\right) \right]\right. \nonumber\\ & \quad \left.\times\, \left[\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \left(\mu_e^{1/2} k_{{\perp}}^2 \rho_i^2 -\frac{1}{2} \mu_e^{1/2} k_{\|}^2 \rho_i^2 + \frac{k_{\|}^2}{k^2}\right)\right]\right\}^{1/2} . \end{align}
\begin{align} \frac{\gamma}{\varOmega_i} & \approx \frac{k_\|}{k} \left\{\left[-\varDelta_i \frac{k_{\bot}^2-k_{\|}^2}{k^2} - k^2 \rho_i^2\left(\frac{1}{\beta_i} +\frac{\mu_e^{1/2} \varDelta_i}{2}\right) \right]\right. \nonumber\\ & \quad \left.\times\, \left[\frac{k^2 \rho_i^2}{\beta_i} - \varDelta_i \left(\mu_e^{1/2} k_{{\perp}}^2 \rho_i^2 -\frac{1}{2} \mu_e^{1/2} k_{\|}^2 \rho_i^2 + \frac{k_{\|}^2}{k^2}\right)\right]\right\}^{1/2} . \end{align}
The bound (4.73) on the total wavenumber required for the instability of modes with ![]() $k_{\perp } > k_{\|}$ is then
$k_{\perp } > k_{\|}$ is then
 \begin{equation} k \rho_i < \sqrt{\frac{|\varDelta_i| \beta_i \left(\sin^2{\theta}-\cos^2{\theta}\right)}{1+\mu_e^{1/2} \varDelta_i \beta_i/2}} . \end{equation}
\begin{equation} k \rho_i < \sqrt{\frac{|\varDelta_i| \beta_i \left(\sin^2{\theta}-\cos^2{\theta}\right)}{1+\mu_e^{1/2} \varDelta_i \beta_i/2}} . \end{equation}
Because the denominator tends to zero as ![]() $\varDelta _i \rightarrow -2 \mu _e^{-1/2} \beta _i^{-1}$, the bound becomes increasingly weak, and so the region of
$\varDelta _i \rightarrow -2 \mu _e^{-1/2} \beta _i^{-1}$, the bound becomes increasingly weak, and so the region of ![]() $(k_{\|},k_{\perp })$-space in which there is instability extends significantly towards electron-Larmor scales. This extension precedes the onset of the oblique electron firehose instability (see § 4.4.7).
$(k_{\|},k_{\perp })$-space in which there is instability extends significantly towards electron-Larmor scales. This extension precedes the onset of the oblique electron firehose instability (see § 4.4.7).
4.4.6. Parallel electron firehose instability
The CES parallel electron firehose instability arises when the negative electron-pressure anisotropy (![]() $\varDelta _e < 0$) associated with the CE electron-shear term becomes a sufficiently large free-energy source to overcome the relatively weak collisionless damping mechanisms that act on long-wavelength (
$\varDelta _e < 0$) associated with the CE electron-shear term becomes a sufficiently large free-energy source to overcome the relatively weak collisionless damping mechanisms that act on long-wavelength (![]() $k_{\|} \rho _e \ll 1$) quasiparallel whistler waves by changing their handedness from right to left handed. More specifically, whistler waves with quasi-parallel wavevectors do not have a component of electric field parallel to
$k_{\|} \rho _e \ll 1$) quasiparallel whistler waves by changing their handedness from right to left handed. More specifically, whistler waves with quasi-parallel wavevectors do not have a component of electric field parallel to ![]() $\boldsymbol {B}_0$, and so are not subject to electron-Landau damping. Electron-cyclotron damping does occur, but is very inefficient for
$\boldsymbol {B}_0$, and so are not subject to electron-Landau damping. Electron-cyclotron damping does occur, but is very inefficient for ![]() $k_{\|} \rho _e \ll 1$. The resonant interaction primarily responsible for damping is that between the whistler waves and Maxwellian ions in the CE plasma streaming along field lines with
$k_{\|} \rho _e \ll 1$. The resonant interaction primarily responsible for damping is that between the whistler waves and Maxwellian ions in the CE plasma streaming along field lines with ![]() $v_{\|} \ll v_{\mathrm {th}i}$. When the handedness of the whistler waves changes, this interaction instead leads to the waves’ growth. Because the resonant interaction driving the instability involves the plasma's ions, the CES parallel electron firehose instability has a rather small growth rate compared with other CES electron-scale microinstabilities, with growth disappearing entirely in the special case of cold ions. The parallel wavenumber of peak growth, which is a small but finite fraction of the electron-Larmor scale, viz.
$v_{\|} \ll v_{\mathrm {th}i}$. When the handedness of the whistler waves changes, this interaction instead leads to the waves’ growth. Because the resonant interaction driving the instability involves the plasma's ions, the CES parallel electron firehose instability has a rather small growth rate compared with other CES electron-scale microinstabilities, with growth disappearing entirely in the special case of cold ions. The parallel wavenumber of peak growth, which is a small but finite fraction of the electron-Larmor scale, viz. ![]() $(k_{\|} \rho _e)_{\rm peak} \approx 0.4$ for
$(k_{\|} \rho _e)_{\rm peak} \approx 0.4$ for ![]() $\varDelta _e \lesssim -2/\beta _e$, is set by electron-cyclotron damping, which prevents shorter-wavelength modes from becoming unstable. The CES parallel electron firehose instability was first identified by Hollweg & Völk (Reference Hollweg and Völk1970) and has been studied subsequently using theory and simulations in plasma with
$\varDelta _e \lesssim -2/\beta _e$, is set by electron-cyclotron damping, which prevents shorter-wavelength modes from becoming unstable. The CES parallel electron firehose instability was first identified by Hollweg & Völk (Reference Hollweg and Völk1970) and has been studied subsequently using theory and simulations in plasma with ![]() $\beta _e \sim 1\unicode{x2013}20$ by a number of authors (e.g. Paesold & Benz Reference Paesold and Benz1999; Li & Habbal Reference Li and Habbal2000; Messmer Reference Messmer2002; Gary & Nishimura Reference Gary and Nishimura2003; Camporeale & Burgess Reference Camporeale and Burgess2008, Reference Camporeale and Burgess2010; Riquelme et al. Reference Riquelme, Quataert and Verscharen2018).
$\beta _e \sim 1\unicode{x2013}20$ by a number of authors (e.g. Paesold & Benz Reference Paesold and Benz1999; Li & Habbal Reference Li and Habbal2000; Messmer Reference Messmer2002; Gary & Nishimura Reference Gary and Nishimura2003; Camporeale & Burgess Reference Camporeale and Burgess2008, Reference Camporeale and Burgess2010; Riquelme et al. Reference Riquelme, Quataert and Verscharen2018).
To characterise the parallel electron firehose instability analytically, we can simply use the expressions (4.21a) and (4.21b) given in § 4.3.2 for the real frequency ![]() $\varpi$ and growth rate
$\varpi$ and growth rate ![]() $\gamma$, respectively, of the parallel whistler waves that satisfy the ordering
$\gamma$, respectively, of the parallel whistler waves that satisfy the ordering
and have ![]() $k_{\|} \rho _e \sim 1$, but this time with
$k_{\|} \rho _e \sim 1$, but this time with ![]() $\varDelta _e \beta _e < 0$. Plots of the dispersion curves
$\varDelta _e \beta _e < 0$. Plots of the dispersion curves ![]() $\varpi (k_{\|})$ and
$\varpi (k_{\|})$ and ![]() $\gamma (k_{\|})$ of CES parallel electron firehose modes are then shown in figure 24 for a selection of different (negative) values of
$\gamma (k_{\|})$ of CES parallel electron firehose modes are then shown in figure 24 for a selection of different (negative) values of ![]() $\varDelta _e \beta _e$. In a hydrogen plasma, we find an instability for
$\varDelta _e \beta _e$. In a hydrogen plasma, we find an instability for ![]() $\varDelta _e < (\varDelta _e)_{c} \approx -1.7/\beta _e$. For
$\varDelta _e < (\varDelta _e)_{c} \approx -1.7/\beta _e$. For ![]() $\varDelta _e \lesssim -2/\beta _e$, modes with
$\varDelta _e \lesssim -2/\beta _e$, modes with ![]() $k_{\|} \rho _e \lesssim 0.4$ become unstable. Figure 24 also shows that parallel electron firehose modes generically have a real frequency that is much greater than their growth rate (
$k_{\|} \rho _e \lesssim 0.4$ become unstable. Figure 24 also shows that parallel electron firehose modes generically have a real frequency that is much greater than their growth rate (![]() $\varpi \sim \varOmega _e/\beta _e \gg \gamma$); however, this frequency changes sign at a wavenumber which, when
$\varpi \sim \varOmega _e/\beta _e \gg \gamma$); however, this frequency changes sign at a wavenumber which, when ![]() $\varDelta _e \lesssim -2/\beta _e$, is comparable to the wavenumber
$\varDelta _e \lesssim -2/\beta _e$, is comparable to the wavenumber ![]() $(k_{\|} \rho _e)_{\rm peak}$ at which peak growth occurs.
$(k_{\|} \rho _e)_{\rm peak}$ at which peak growth occurs.

Figure 24. Parallel CES electron firehose instability. Dispersion curves of unstable whistler modes, whose instability is driven by the negative electron-pressure anisotropy associated with the electron-shear term in CE distribution function (4.1), for wavevectors that are co-parallel with the background magnetic field (viz. ![]() $\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The frequency (solid blue) and growth rates (solid red) of the modes are calculated using (4.21a) and (4.21b), respectively. The resulting frequencies and growth rates, when normalised as
$\boldsymbol {k} = k_{\|} \hat {\boldsymbol {z}}$). The frequency (solid blue) and growth rates (solid red) of the modes are calculated using (4.21a) and (4.21b), respectively. The resulting frequencies and growth rates, when normalised as ![]() $\gamma \beta _e/\varOmega _e$, are functions of the dimensionless quantity
$\gamma \beta _e/\varOmega _e$, are functions of the dimensionless quantity ![]() $\varDelta _e \beta _e$; we show the dispersion curves for three different values of
$\varDelta _e \beta _e$; we show the dispersion curves for three different values of ![]() $\varDelta _e \beta _e$. The
$\varDelta _e \beta _e$. The ![]() $k_{\|} \rho _e \ll 1$ approximations (4.79a) for the frequency (dotted-blue) and (4.79b) growth rate (dotted-red) are also plotted.
$k_{\|} \rho _e \ll 1$ approximations (4.79a) for the frequency (dotted-blue) and (4.79b) growth rate (dotted-red) are also plotted.
These results can be elucidated by considering the expressions (4.21) in the subsidiary limit
 \begin{equation} k_{\|} \rho_i \sim \frac{1}{\sqrt{\log{\left(2 \mu_e^{{-}1/2}|1+2/\varDelta_e \beta_e|\right)}}} \ll 1 . \end{equation}
\begin{equation} k_{\|} \rho_i \sim \frac{1}{\sqrt{\log{\left(2 \mu_e^{{-}1/2}|1+2/\varDelta_e \beta_e|\right)}}} \ll 1 . \end{equation}Then (4.21) simplifies to
 $$\begin{align}\gamma &= \frac{\sqrt{\rm \pi}}{k_\| \rho_e} \left[\varDelta_e \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)}-\left(\frac{\varDelta_e}{2} + \frac{1}{\beta_e}\right) \mu_e^{1/2} k_\|^2 \rho_e^2 \right] \varOmega_e . \end{align}$$
$$\begin{align}\gamma &= \frac{\sqrt{\rm \pi}}{k_\| \rho_e} \left[\varDelta_e \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)}-\left(\frac{\varDelta_e}{2} + \frac{1}{\beta_e}\right) \mu_e^{1/2} k_\|^2 \rho_e^2 \right] \varOmega_e . \end{align}$$
These approximations are plotted alongside (4.21) in figure 24; the agreement is qualitative rather than quantitative for ![]() $\varDelta _e \sim -2/\beta _e$, but becomes increasingly good as
$\varDelta _e \sim -2/\beta _e$, but becomes increasingly good as ![]() $\varDelta _e$ is decreased further.
$\varDelta _e$ is decreased further.
Using these simplified expressions, we can derive approximate analytical expressions for the instability's threshold ![]() $(\varDelta _e)_{c}$, as well as its peak growth rate and the wavenumber at which that growth occurs. First considering the sign of (4.79), it is easy to show that there exists a range of wavenumbers
$(\varDelta _e)_{c}$, as well as its peak growth rate and the wavenumber at which that growth occurs. First considering the sign of (4.79), it is easy to show that there exists a range of wavenumbers ![]() $k_{\|}$ at which
$k_{\|}$ at which ![]() $\gamma > 0$ if and only if
$\gamma > 0$ if and only if ![]() $\varDelta _e < -2/\beta _e$, so
$\varDelta _e < -2/\beta _e$, so ![]() $(\varDelta _e)_{\rm c} \approx -2/\beta _e$. This is somewhat more stringent than the numerically observed threshold, a discrepancy attributable to FLR effects, not taken into account by the approximation (4.79b). When
$(\varDelta _e)_{\rm c} \approx -2/\beta _e$. This is somewhat more stringent than the numerically observed threshold, a discrepancy attributable to FLR effects, not taken into account by the approximation (4.79b). When ![]() $\varDelta _e < -2/\beta _e$, it can be proven that the growth rate (4.79b) is maximised at
$\varDelta _e < -2/\beta _e$, it can be proven that the growth rate (4.79b) is maximised at
 \begin{align} (k_{\|} \rho_e)_{\rm peak} \approx \frac{1}{\sqrt{\log{\left(\mu_e^{{-}1/2}|1/2+1/\varDelta_e \beta_e|\right)}}} \left\{1-\frac{\log{\left[\sqrt{2}\log{\left(\mu_e^{{-}1/2}|1/2+1/\varDelta_e \beta_e|\right)}\right]}}{\log{\left(\mu_e^{{-}1/2}|1/2+1/\varDelta_e \beta_e|\right)}}\right\} , \end{align}
\begin{align} (k_{\|} \rho_e)_{\rm peak} \approx \frac{1}{\sqrt{\log{\left(\mu_e^{{-}1/2}|1/2+1/\varDelta_e \beta_e|\right)}}} \left\{1-\frac{\log{\left[\sqrt{2}\log{\left(\mu_e^{{-}1/2}|1/2+1/\varDelta_e \beta_e|\right)}\right]}}{\log{\left(\mu_e^{{-}1/2}|1/2+1/\varDelta_e \beta_e|\right)}}\right\} , \end{align}attaining the value
Comparing (4.81) with the characteristic magnitude of ![]() $\varpi$ evaluated using (4.79a) at
$\varpi$ evaluated using (4.79a) at ![]() $k_{\|} \rho _e = (k_{\|} \rho _e)_{\rm peak}$ (and assuming that
$k_{\|} \rho _e = (k_{\|} \rho _e)_{\rm peak}$ (and assuming that ![]() $(k_{\|} \rho _e)_{\rm peak} \gtrsim \mu _e^{1/4}$), we conclude that
$(k_{\|} \rho _e)_{\rm peak} \gtrsim \mu _e^{1/4}$), we conclude that ![]() $\gamma \lesssim \mu _e^{1/4} \varpi$, thereby explaining our previous observation that the growth rate of parallel electron firehose modes is generically much smaller than the real frequency of those modes. We can also show that the one exception to this occurs when
$\gamma \lesssim \mu _e^{1/4} \varpi$, thereby explaining our previous observation that the growth rate of parallel electron firehose modes is generically much smaller than the real frequency of those modes. We can also show that the one exception to this occurs when ![]() $(k_{\|} \rho _e)_{\rm peak} \approx \mu _e^{1/4} [2 \varDelta _e \beta _e/(1+2 \varDelta _e \beta _e)]^{1/2}$, an approximate expression for the wavenumber below which
$(k_{\|} \rho _e)_{\rm peak} \approx \mu _e^{1/4} [2 \varDelta _e \beta _e/(1+2 \varDelta _e \beta _e)]^{1/2}$, an approximate expression for the wavenumber below which ![]() $\varpi$ changes sign. As we will see, the characteristic growth rate of the CES parallel electron firehose is typically much smaller than its oblique relative in high-
$\varpi$ changes sign. As we will see, the characteristic growth rate of the CES parallel electron firehose is typically much smaller than its oblique relative in high-![]() $\beta$ plasma (see § 4.4.7), a conclusion that also applies in
$\beta$ plasma (see § 4.4.7), a conclusion that also applies in ![]() $\beta _e \sim 1$ plasmas with bi-Maxwellian distributions (see Li & Habbal Reference Li and Habbal2000).
$\beta _e \sim 1$ plasmas with bi-Maxwellian distributions (see Li & Habbal Reference Li and Habbal2000).
4.4.7. Oblique electron firehose instability
In spite of its similar name, the CES oblique electron firehose instability is quite distinct from its parallel cousin: it is a non-propagating mode than arises from the destabilisation of oblique KAWs by a sufficiently negative electron-pressure anisotropy. The linear theory of the analogous instability in ![]() $\beta _e \sim 1$ plasma with bi-Maxwellian electrons was first presented by Li & Habbal (Reference Li and Habbal2000), with a number of simulation studies of this instability having been conducted subsequently (Gary & Nishimura Reference Gary and Nishimura2003; Camporeale & Burgess Reference Camporeale and Burgess2008, Reference Camporeale and Burgess2010; Riquelme et al. Reference Riquelme, Quataert and Verscharen2018). The high-
$\beta _e \sim 1$ plasma with bi-Maxwellian electrons was first presented by Li & Habbal (Reference Li and Habbal2000), with a number of simulation studies of this instability having been conducted subsequently (Gary & Nishimura Reference Gary and Nishimura2003; Camporeale & Burgess Reference Camporeale and Burgess2008, Reference Camporeale and Burgess2010; Riquelme et al. Reference Riquelme, Quataert and Verscharen2018). The high-![]() $\beta$ variant of the (linear) instability for general anisotropic electron distribution functions was studied in the
$\beta$ variant of the (linear) instability for general anisotropic electron distribution functions was studied in the ![]() $k_{\|} \ll k_{\perp }$ limit of gyrokinetics by Kunz et al. (Reference Kunz, Abel, Klein and Schekochihin2018). In contrast to the findings of Gary & Nishimura (Reference Gary and Nishimura2003), who showed that the oblique electron firehose instability in a bi-Maxwellian plasma at
$k_{\|} \ll k_{\perp }$ limit of gyrokinetics by Kunz et al. (Reference Kunz, Abel, Klein and Schekochihin2018). In contrast to the findings of Gary & Nishimura (Reference Gary and Nishimura2003), who showed that the oblique electron firehose instability in a bi-Maxwellian plasma at ![]() $\beta _e \sim 1$ involves gyroresonant wave–particle interactions between electrons and the unstable modes, instability of CES oblique electron firehose modes at
$\beta _e \sim 1$ involves gyroresonant wave–particle interactions between electrons and the unstable modes, instability of CES oblique electron firehose modes at ![]() $\beta _e \gg 1$ is essentially non-resonant, with sufficient large negative electron-pressure anisotropies negating the restoring force that underpins the oscillation of high-
$\beta _e \gg 1$ is essentially non-resonant, with sufficient large negative electron-pressure anisotropies negating the restoring force that underpins the oscillation of high-![]() $\beta$ KAWs.
$\beta$ KAWs.
Similarly to the parallel electron firehose instability, the CES oblique electron firehose instability is triggered when ![]() $\varDelta _e \lesssim -2/\beta _e$. The precise value of the threshold depends on the wavevector of the mode being destabilised. Analogously to the parallel electron firehose, long-wavelength oblique electron firehose modes are unstable when
$\varDelta _e \lesssim -2/\beta _e$. The precise value of the threshold depends on the wavevector of the mode being destabilised. Analogously to the parallel electron firehose, long-wavelength oblique electron firehose modes are unstable when ![]() $\varDelta _e < (\varDelta _e)_{c} = -2/\beta _e$. However, figure 25(a) shows that there is positive growth of
$\varDelta _e < (\varDelta _e)_{c} = -2/\beta _e$. However, figure 25(a) shows that there is positive growth of ![]() $k \rho _e \sim 1$ oblique electron firehose modes for less negative values of
$k \rho _e \sim 1$ oblique electron firehose modes for less negative values of ![]() $\varDelta _e$, illustrating that the threshold is less stringent for such modes. This phenomenon is reminiscent of the ion firehose instability (see figure 20): ion-Larmor-scale oblique firehose modes also have a less stringent threshold than longer-wavelength modes. In addition to the
$\varDelta _e$, illustrating that the threshold is less stringent for such modes. This phenomenon is reminiscent of the ion firehose instability (see figure 20): ion-Larmor-scale oblique firehose modes also have a less stringent threshold than longer-wavelength modes. In addition to the ![]() $k \rho _e \sim 1$ modes, a region of unstable KAWs with characteristic wavenumbers
$k \rho _e \sim 1$ modes, a region of unstable KAWs with characteristic wavenumbers ![]() $\mu _e^{1/2} \ll k \rho _e \ll \mu _e^{1/4}$,
$\mu _e^{1/2} \ll k \rho _e \ll \mu _e^{1/4}$, ![]() $k_{\bot } \sim k_{\|}$, is evident in figure 25(a). These modes, which were discussed at the end of § 4.4.1, are destabilised by negative ion-pressure anisotropy; the extent of this region closely matches the analytic prediction (4.76). Using a similar semi-analytic approach to that employed for the case of the ion firehose instability (see Appendix K.2.2), we can determine the approximate threshold for the oblique electron firehose instability as a function of
$k_{\bot } \sim k_{\|}$, is evident in figure 25(a). These modes, which were discussed at the end of § 4.4.1, are destabilised by negative ion-pressure anisotropy; the extent of this region closely matches the analytic prediction (4.76). Using a similar semi-analytic approach to that employed for the case of the ion firehose instability (see Appendix K.2.2), we can determine the approximate threshold for the oblique electron firehose instability as a function of ![]() $k_{\|} \rho _e$ and
$k_{\|} \rho _e$ and ![]() $k_{\perp } \rho _e$. The results are shown in figure 25(b); modes with
$k_{\perp } \rho _e$. The results are shown in figure 25(b); modes with ![]() $k_{\|} \rho _e \sim 0.5$,
$k_{\|} \rho _e \sim 0.5$, ![]() $k_{\perp } \rho _e \sim 0.4$ have the least stringent threshold (
$k_{\perp } \rho _e \sim 0.4$ have the least stringent threshold (![]() $\varDelta _e \approx -1.4/\beta _e$).
$\varDelta _e \approx -1.4/\beta _e$).

Figure 25. Onset of the CES oblique electron firehose instability. (a) Maximum positive growth rates of linear perturbations resulting from both the CE ion- and electron-shear term in the CE distribution function (4.1) with ![]() $\beta _i = 10^{4}$ and
$\beta _i = 10^{4}$ and ![]() $\varDelta _e = -1.7/\beta _e$ (which is above the long-wavelength oblique electron-firehose instability-threshold
$\varDelta _e = -1.7/\beta _e$ (which is above the long-wavelength oblique electron-firehose instability-threshold ![]() $\varDelta _e = -2/\beta _e$). The growth rates of all modes are calculated in the same way as figure 19. The resulting growth rates are normalised as
$\varDelta _e = -2/\beta _e$). The growth rates of all modes are calculated in the same way as figure 19. The resulting growth rates are normalised as ![]() $\gamma \beta _e/\varOmega _e$ are functions of the dimensionless parameter
$\gamma \beta _e/\varOmega _e$ are functions of the dimensionless parameter ![]() $\varDelta _e \beta _e$. The dotted line denotes the instability boundary (4.76) on KAWs driven unstable by ion-pressure anisotropy of the CE ion-shear term. (b) Threshold value of
$\varDelta _e \beta _e$. The dotted line denotes the instability boundary (4.76) on KAWs driven unstable by ion-pressure anisotropy of the CE ion-shear term. (b) Threshold value of ![]() $\varDelta _e \beta _e$ at which modes with parallel and perpendicular wavenumber
$\varDelta _e \beta _e$ at which modes with parallel and perpendicular wavenumber ![]() $k_{\|}$ and
$k_{\|}$ and ![]() $k_{\perp }$, respectively, become unstable. Regions of
$k_{\perp }$, respectively, become unstable. Regions of ![]() $(k_{\|},k_{\perp })$ that are shaded black are stable.
$(k_{\|},k_{\perp })$ that are shaded black are stable.
Well into the unstable regime, i.e. when ![]() $\varDelta _e\beta _e + 2 \lesssim -1$, electron firehose modes across a broad range of wavevectors are destabilised (see figure 26a). The fastest-growing electron firehose modes are oblique and occur at electron-Larmor scales (
$\varDelta _e\beta _e + 2 \lesssim -1$, electron firehose modes across a broad range of wavevectors are destabilised (see figure 26a). The fastest-growing electron firehose modes are oblique and occur at electron-Larmor scales (![]() $k_{\perp } \rho _e \sim 1 > k_{\|} \rho _e$), with characteristic growth rate
$k_{\perp } \rho _e \sim 1 > k_{\|} \rho _e$), with characteristic growth rate ![]() $\gamma \sim |\varDelta _e| \varOmega _e \sim \varOmega _e/\beta _e$. This growth rate is much larger than the peak growth rate of the parallel electron firehose instability (4.81).
$\gamma \sim |\varDelta _e| \varOmega _e \sim \varOmega _e/\beta _e$. This growth rate is much larger than the peak growth rate of the parallel electron firehose instability (4.81).

Figure 26. Oblique electron firehose instability at ![]() $\varDelta _e \beta _e +2 \lesssim -1$. (a) Maximum positive growth rates of linear perturbations resulting from CE ion- and electron-shear terms in the CE distribution function (4.1) for
$\varDelta _e \beta _e +2 \lesssim -1$. (a) Maximum positive growth rates of linear perturbations resulting from CE ion- and electron-shear terms in the CE distribution function (4.1) for ![]() $\varDelta _e \beta _e = -3$. Here, a temperature-equilibrated hydrogen plasma is considered, viz.
$\varDelta _e \beta _e = -3$. Here, a temperature-equilibrated hydrogen plasma is considered, viz. ![]() $\varDelta _e = \mu _e^{1/2} \varDelta _i$, and
$\varDelta _e = \mu _e^{1/2} \varDelta _i$, and ![]() $\beta _i = \beta _e$. The growth rates of all modes are calculated in the same way as figure 25. (b) Plots of the oblique electron firehose mode growth rate (solid line) as a function of
$\beta _i = \beta _e$. The growth rates of all modes are calculated in the same way as figure 25. (b) Plots of the oblique electron firehose mode growth rate (solid line) as a function of ![]() $k_{\|} \rho _e$ with
$k_{\|} \rho _e$ with ![]() $k_{\bot } \rho _e = 0.2$ (top), and as a function of
$k_{\bot } \rho _e = 0.2$ (top), and as a function of ![]() $k_{\perp } \rho _e$ with
$k_{\perp } \rho _e$ with ![]() $k_{\|} \rho _e = 0.2$ (bottom). The dotted and dashed lines show the analytical predictions (4.83) and (4.86), respectively.
$k_{\|} \rho _e = 0.2$ (bottom). The dotted and dashed lines show the analytical predictions (4.83) and (4.86), respectively.
Similarly to the electron mirror instability, a simple analytic expression for the growth rate of the fastest-growing electron firehose modes when ![]() $\varDelta _e\beta _e + 2 \lesssim -1$ is challenging to establish. We can, however, characterise the growth of two particular classes of electron firehose modes analytically.
$\varDelta _e\beta _e + 2 \lesssim -1$ is challenging to establish. We can, however, characterise the growth of two particular classes of electron firehose modes analytically.
The first of these are long-wavelength (viz. ![]() $k \rho _e \ll 1$) electron firehose modes. For these, we adopt the same ordering (4.38) as was considered when characterising long-wavelength electron mirror modes:
$k \rho _e \ll 1$) electron firehose modes. For these, we adopt the same ordering (4.38) as was considered when characterising long-wavelength electron mirror modes:
We then obtain a closed-form expression (cf. (4.39), and also (4.75)) for the complex frequencies of the electron firehose modes:
 \begin{align} \omega & \approx{\pm} k_\| \rho_e \varOmega_e \left\{\left[\frac{1}{\beta_e} + \varDelta_e\left(\frac{1}{2}- \mu_e^{1/2} \frac{k_{\|}^2 \rho_e^2- k_{\bot}^2 \rho_e^2}{k^4 \rho_e^4}\right) \right]\right.\nonumber\\ &\left. \quad \times \left[ \frac{k^2 \rho_e^2}{\beta_e} - \varDelta_e \left(k_{\bot}^2 \rho_e^2 + \mu_e^{1/2} \frac{k_{\|}^2}{k^2} - \frac{1}{2} k_{\|}^2 \rho_e^2 \right) \right]\right\}^{1/2} . \end{align}
\begin{align} \omega & \approx{\pm} k_\| \rho_e \varOmega_e \left\{\left[\frac{1}{\beta_e} + \varDelta_e\left(\frac{1}{2}- \mu_e^{1/2} \frac{k_{\|}^2 \rho_e^2- k_{\bot}^2 \rho_e^2}{k^4 \rho_e^4}\right) \right]\right.\nonumber\\ &\left. \quad \times \left[ \frac{k^2 \rho_e^2}{\beta_e} - \varDelta_e \left(k_{\bot}^2 \rho_e^2 + \mu_e^{1/2} \frac{k_{\|}^2}{k^2} - \frac{1}{2} k_{\|}^2 \rho_e^2 \right) \right]\right\}^{1/2} . \end{align}
If ![]() $\varDelta _e < -2/\beta _e$, the right-hand side of (4.83) is purely imaginary for
$\varDelta _e < -2/\beta _e$, the right-hand side of (4.83) is purely imaginary for ![]() $k_{\perp } > k_{\|}$, and so we have positive growth for all long-wavelength electron firehose modes with
$k_{\perp } > k_{\|}$, and so we have positive growth for all long-wavelength electron firehose modes with ![]() $\theta > 45^{\circ }$.Footnote 7 This approximation should be compared with the numerically determined growth rate in figure 26(b). If it is further assumed that
$\theta > 45^{\circ }$.Footnote 7 This approximation should be compared with the numerically determined growth rate in figure 26(b). If it is further assumed that ![]() $\mu _e^{1/4} \ll k \rho _e \ll 1$,
$\mu _e^{1/4} \ll k \rho _e \ll 1$, ![]() $k_{\bot } \sim k_{\|}$, it is shown in § 4.3.4 that (4.83) simplifies to an analogue of (4.40), viz.
$k_{\bot } \sim k_{\|}$, it is shown in § 4.3.4 that (4.83) simplifies to an analogue of (4.40), viz.
 \begin{equation} \omega \approx{\pm} k_\| \rho_e \varOmega_e \sqrt{\left(\frac{1}{\beta_e} + \frac{\varDelta_e}{2}\right)\left(k^2 \rho_e^2 \frac{1}{\beta_e} + \frac{\varDelta_e}{2} \left[k_{\|}^2 \rho_e^2 -2 k_{\bot}^2 \rho_e^2 \right] \right)} . \end{equation}
\begin{equation} \omega \approx{\pm} k_\| \rho_e \varOmega_e \sqrt{\left(\frac{1}{\beta_e} + \frac{\varDelta_e}{2}\right)\left(k^2 \rho_e^2 \frac{1}{\beta_e} + \frac{\varDelta_e}{2} \left[k_{\|}^2 \rho_e^2 -2 k_{\bot}^2 \rho_e^2 \right] \right)} . \end{equation}
This result is again in agreement with the gyrokinetic calculations of Kunz et al. (Reference Kunz, Abel, Klein and Schekochihin2018). Extrapolating (4.84) to ![]() $k_{\|} \rho _e \sim k_{\perp } \rho _e \sim 1$, we recover that
$k_{\|} \rho _e \sim k_{\perp } \rho _e \sim 1$, we recover that ![]() $\gamma \sim \varOmega _e/\beta _e$ when
$\gamma \sim \varOmega _e/\beta _e$ when ![]() $|\varDelta _e \beta _e + 2| \gtrsim 1$.
$|\varDelta _e \beta _e + 2| \gtrsim 1$.
A second sub-category of electron firehose modes that can be described analytically are quasi-perpendicular ones. For any fixed ![]() $k_{\|} \rho _e \ll 1$, the most rapidly growing modes are strongly anisotropic: they occur when the perpendicular wavelength is comparable to the electron Larmor radius,
$k_{\|} \rho _e \ll 1$, the most rapidly growing modes are strongly anisotropic: they occur when the perpendicular wavelength is comparable to the electron Larmor radius, ![]() $k_{\bot } \rho _e \sim 1$. These modes can therefore be elucidated analytically by considering their dispersion relation under the ordering
$k_{\bot } \rho _e \sim 1$. These modes can therefore be elucidated analytically by considering their dispersion relation under the ordering
in the wavenumber domain ![]() $\mu _e^{1/2} \ll k_{\|} \rho _e \ll k_{\bot } \rho _e \sim 1$. We solve the dispersion relation (see Appendix K.3.10) to find
$\mu _e^{1/2} \ll k_{\|} \rho _e \ll k_{\bot } \rho _e \sim 1$. We solve the dispersion relation (see Appendix K.3.10) to find
where the discriminant is
 \begin{align} \mathfrak{D}\left(k_{\bot} \rho_e, \beta_e, \varDelta_e\right) & \equiv \left[\frac{k_{\bot}^2 \rho_e^2}{\beta_e}+\varDelta_e \mathcal{H}(k_{{\perp}} \rho_e) \right] \nonumber\\ & \quad \times \left\{\frac{1}{\beta_e} \left(1-\frac{\rm \pi}{4} k_{\bot}^2 \rho_e^2 \right) - \varDelta_e \left[\frac{\rm \pi}{4} \mathcal{H}(k_{{\perp}} \rho_e) + \mathcal{F}(k_{{\perp}} \rho_e) \right] \right\} , \end{align}
\begin{align} \mathfrak{D}\left(k_{\bot} \rho_e, \beta_e, \varDelta_e\right) & \equiv \left[\frac{k_{\bot}^2 \rho_e^2}{\beta_e}+\varDelta_e \mathcal{H}(k_{{\perp}} \rho_e) \right] \nonumber\\ & \quad \times \left\{\frac{1}{\beta_e} \left(1-\frac{\rm \pi}{4} k_{\bot}^2 \rho_e^2 \right) - \varDelta_e \left[\frac{\rm \pi}{4} \mathcal{H}(k_{{\perp}} \rho_e) + \mathcal{F}(k_{{\perp}} \rho_e) \right] \right\} , \end{align}and the two auxiliary functions are (cf. (3.24))
As a sanity check, we observe that in the subsidiary limit ![]() $k_{\bot } \rho _e \ll 1$, (4.86) becomes
$k_{\bot } \rho _e \ll 1$, (4.86) becomes
 \begin{equation} \omega \approx{\pm} k_{\bot} k_{\|} \rho_e^2 \varOmega_e \sqrt{\left(\frac{1}{\beta_e} + \frac{\varDelta_e}{2}\right)\left(\frac{1}{\beta_e} -\varDelta_e \right)} , \end{equation}
\begin{equation} \omega \approx{\pm} k_{\bot} k_{\|} \rho_e^2 \varOmega_e \sqrt{\left(\frac{1}{\beta_e} + \frac{\varDelta_e}{2}\right)\left(\frac{1}{\beta_e} -\varDelta_e \right)} , \end{equation}
returning us to the dispersion relation (4.84) of unstable kinetic Alfvén waves taken in the limit ![]() $k_{\|} \ll k_{\bot }$.
$k_{\|} \ll k_{\bot }$.
In the case when ![]() $\varDelta _e < -2 \beta _e^{-1}$, one of the modes described by (4.86) can be destabilised by sufficiently negative pressure anisotropy, and become purely growing. The wavenumbers susceptible to this instability are those satisfying
$\varDelta _e < -2 \beta _e^{-1}$, one of the modes described by (4.86) can be destabilised by sufficiently negative pressure anisotropy, and become purely growing. The wavenumbers susceptible to this instability are those satisfying
 \begin{equation} k_{\bot}^2 \rho_e^2 \left[1 - \exp \left(-\frac{k_{\bot}^2 \rho_e^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right)\right]^{{-}1} < |\varDelta_e| \beta_e . \end{equation}
\begin{equation} k_{\bot}^2 \rho_e^2 \left[1 - \exp \left(-\frac{k_{\bot}^2 \rho_e^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right)\right]^{{-}1} < |\varDelta_e| \beta_e . \end{equation}
Provided ![]() $\varDelta _e < -2 \beta _e^{-1}$ and
$\varDelta _e < -2 \beta _e^{-1}$ and ![]() $|\varDelta _e| \beta _e \sim 1$, this gives a range of unstable perpendicular wavenumbers
$|\varDelta _e| \beta _e \sim 1$, this gives a range of unstable perpendicular wavenumbers ![]() $k_{\bot } \rho _e \lesssim 1$. That these wavenumbers are indeed unstable follows immediately from the observation that if (4.91) holds, then the discriminant (4.87) satisfies
$k_{\bot } \rho _e \lesssim 1$. That these wavenumbers are indeed unstable follows immediately from the observation that if (4.91) holds, then the discriminant (4.87) satisfies
 \begin{align} \mathfrak{D}\left(k_{\bot} \rho_e, \beta_e, \varDelta_e\right) & ={-}{\rm \pi} \left[\varDelta_e \mathcal{H}(k_{{\perp}} \rho_e)-\frac{k_{\bot}^2 \rho_e^2}{\beta_e}\right] \left[\varDelta_e \mathcal{H}(k_{{\perp}} \rho_e)-\frac{k_{\bot}^2 \rho_e^2}{\beta_e}+ \frac{1}{\beta_e} +|\varDelta_e| \mathcal{F}(k_{{\perp}} \rho_e)\right] \nonumber\\ & < {\rm \pi}\left[\varDelta_e \mathcal{H}(k_{{\perp}} \rho_e)-\frac{k_{\bot}^2 \rho_e^2}{\beta_e}\right]^2 , \end{align}
\begin{align} \mathfrak{D}\left(k_{\bot} \rho_e, \beta_e, \varDelta_e\right) & ={-}{\rm \pi} \left[\varDelta_e \mathcal{H}(k_{{\perp}} \rho_e)-\frac{k_{\bot}^2 \rho_e^2}{\beta_e}\right] \left[\varDelta_e \mathcal{H}(k_{{\perp}} \rho_e)-\frac{k_{\bot}^2 \rho_e^2}{\beta_e}+ \frac{1}{\beta_e} +|\varDelta_e| \mathcal{F}(k_{{\perp}} \rho_e)\right] \nonumber\\ & < {\rm \pi}\left[\varDelta_e \mathcal{H}(k_{{\perp}} \rho_e)-\frac{k_{\bot}^2 \rho_e^2}{\beta_e}\right]^2 , \end{align}
from which it follows that the imaginary part of (4.86) for the ‘![]() $+$’ root is positive. When
$+$’ root is positive. When ![]() $|\varDelta _e \beta _e + 2| \sim 1$, the characteristic growth rate of the instability is
$|\varDelta _e \beta _e + 2| \sim 1$, the characteristic growth rate of the instability is
which is consistent with the numerical findings shown in figure 26(a). Indeed, (4.86) agrees reasonably with the numerically determined growth rate for small values of ![]() $k_{\|} \rho _i$ (see figure 26b).
$k_{\|} \rho _i$ (see figure 26b).
One particularly interesting subsidiary limit of (4.90) is ![]() $|\varDelta _e| \beta _e \gg 1$, in which it can be shown that, under the ordering
$|\varDelta _e| \beta _e \gg 1$, in which it can be shown that, under the ordering ![]() $k_{\bot } \rho _e \sim (|\varDelta _e| \beta _e)^{1/2} \gg 1$, the growth rate is
$k_{\bot } \rho _e \sim (|\varDelta _e| \beta _e)^{1/2} \gg 1$, the growth rate is
This implies that the perpendicular wavelength of peak growth transitions smoothly to values below the electron-Larmor radius as ![]() $|\varDelta _e| \beta _e$ is increased beyond order-unity values. As we shall discuss in the next section, these unstable sub-electron-Larmor-scale modes are best regarded as a distinct instability from the electron firehose, and so we introduce it properly in a new section.
$|\varDelta _e| \beta _e$ is increased beyond order-unity values. As we shall discuss in the next section, these unstable sub-electron-Larmor-scale modes are best regarded as a distinct instability from the electron firehose, and so we introduce it properly in a new section.
4.4.8. Electron-scale-transition instability
When ![]() $|\varDelta _e| \beta _e$ is increased significantly past unity, the fastest-growing microinstability changes character from that of a destabilised KAW, and instead becomes a destabilised non-propagating mode. The authors of this paper are not aware of this instability having been identified previously; we call it the EST instability, on account of it providing a smooth transition between unstable KAWs with
$|\varDelta _e| \beta _e$ is increased significantly past unity, the fastest-growing microinstability changes character from that of a destabilised KAW, and instead becomes a destabilised non-propagating mode. The authors of this paper are not aware of this instability having been identified previously; we call it the EST instability, on account of it providing a smooth transition between unstable KAWs with ![]() $k_{\bot } \rho _e \ll 1$, and microinstabilities on sub-electron scales (
$k_{\bot } \rho _e \ll 1$, and microinstabilities on sub-electron scales (![]() $k_{\bot } \rho _e \gtrsim 1$). Unstable EST modes are quasi-perpendicular (
$k_{\bot } \rho _e \gtrsim 1$). Unstable EST modes are quasi-perpendicular (![]() $k_{\|} \rho _e < 1 \lesssim k_{\bot } \rho _e \lesssim \beta _e^{1/7}$), with the parallel wavenumber of the fastest-growing modes determined by a balance between the instability's drive and the electron-cyclotron damping that arises at sufficiently large
$k_{\|} \rho _e < 1 \lesssim k_{\bot } \rho _e \lesssim \beta _e^{1/7}$), with the parallel wavenumber of the fastest-growing modes determined by a balance between the instability's drive and the electron-cyclotron damping that arises at sufficiently large ![]() $k_{\|} \rho _e$. In contrast to the oblique electron firehose instability, Landau-resonant electrons with
$k_{\|} \rho _e$. In contrast to the oblique electron firehose instability, Landau-resonant electrons with ![]() $v_{\|} \approx \omega /k_{\|}$ also play a role in the EST instability's physical mechanism.
$v_{\|} \approx \omega /k_{\|}$ also play a role in the EST instability's physical mechanism.
To demonstrate that the EST modes are not unstable KAWs, we consider the expression (4.86) in a Maxwellian plasma (viz. ![]() $\varDelta _e = 0$). It is easy to show that in this case,
$\varDelta _e = 0$). It is easy to show that in this case, ![]() $\mathfrak {D}(k_{\bot } \rho _e, \beta _e, \varDelta _e) \leqslant 0$ if and only if
$\mathfrak {D}(k_{\bot } \rho _e, \beta _e, \varDelta _e) \leqslant 0$ if and only if
Thus, for sufficiently large values of ![]() $k_{\bot } \rho _e$, KAWs cease to be able to propagate, and we obtain two purely damped non-propagating modes. Thus, any microinstabilities for
$k_{\bot } \rho _e$, KAWs cease to be able to propagate, and we obtain two purely damped non-propagating modes. Thus, any microinstabilities for ![]() $\varDelta _e < 0$ associated with these modes can no longer be considered to be unstable KAWs. Substituting (4.95) into the threshold condition (4.91), we estimate that EST modes first become unstable when
$\varDelta _e < 0$ associated with these modes can no longer be considered to be unstable KAWs. Substituting (4.95) into the threshold condition (4.91), we estimate that EST modes first become unstable when ![]() $\varDelta _e < (\varDelta _e)_{\rm c} \approx -3/\beta _e$.
$\varDelta _e < (\varDelta _e)_{\rm c} \approx -3/\beta _e$.
As ![]() $\varDelta _e$ is decreased below
$\varDelta _e$ is decreased below ![]() $(\varDelta _e)_{\rm c}$, the EST modes quickly acquire a faster growth rate than all the other CES microinstabilities that can operate for such values of
$(\varDelta _e)_{\rm c}$, the EST modes quickly acquire a faster growth rate than all the other CES microinstabilities that can operate for such values of ![]() $\varDelta _e$. We illustrate this numerically in figure 27(a) by showing the maximum growth rate of all CES microinstabilities as a function of
$\varDelta _e$. We illustrate this numerically in figure 27(a) by showing the maximum growth rate of all CES microinstabilities as a function of ![]() $(k_{\|},k_{\perp })$ for a particular value of
$(k_{\|},k_{\perp })$ for a particular value of ![]() $\varDelta _e < 0$. The EST modes with
$\varDelta _e < 0$. The EST modes with ![]() $k_{\|} \rho _e$,
$k_{\|} \rho _e$, ![]() $k_{\perp } \rho _e > 1$ are the fastest growing, with
$k_{\perp } \rho _e > 1$ are the fastest growing, with ![]() $\gamma \gg \varOmega _e/\beta _e$.
$\gamma \gg \varOmega _e/\beta _e$.

Figure 27. The CES EST instability. (a) Maximum positive growth rates of linear perturbations resulting from CE ion- and electron-shear terms in the CE distribution function (4.1) for ![]() $\varDelta _e \beta _e = -10$ and
$\varDelta _e \beta _e = -10$ and ![]() $\beta _e = 10^4$. Here, a temperature-equilibrated hydrogen plasma is considered viz.
$\beta _e = 10^4$. Here, a temperature-equilibrated hydrogen plasma is considered viz. ![]() $\varDelta _e = \mu _e^{1/2} \varDelta _i$, and
$\varDelta _e = \mu _e^{1/2} \varDelta _i$, and ![]() $\beta _i = \beta _e$. The growth rates of all modes are calculated in the same way as figure 25. (b) Plot of the EST mode growth rate (solid line) as a function of
$\beta _i = \beta _e$. The growth rates of all modes are calculated in the same way as figure 25. (b) Plot of the EST mode growth rate (solid line) as a function of ![]() $k_{\|} \rho _e$ with
$k_{\|} \rho _e$ with ![]() $k_{\bot } \rho _e = (3 |\varDelta _e|\beta _e/5)^{1/2}$ (top), and as a function of
$k_{\bot } \rho _e = (3 |\varDelta _e|\beta _e/5)^{1/2}$ (top), and as a function of ![]() $k_{\perp } \rho _e$ with
$k_{\perp } \rho _e$ with ![]() $k_{\|} \rho _e = (k_{\|} \rho _e)_{\rm peak}$ (bottom), where
$k_{\|} \rho _e = (k_{\|} \rho _e)_{\rm peak}$ (bottom), where ![]() $(k_{\|} \rho _e)_{\rm peak}$ is given by (4.99b). The dotted and dashed lines show the analytical prediction (4.97).
$(k_{\|} \rho _e)_{\rm peak}$ is given by (4.99b). The dotted and dashed lines show the analytical prediction (4.97).
In the limit ![]() $|\varDelta _e| \beta _e \gg 1$ (but
$|\varDelta _e| \beta _e \gg 1$ (but ![]() $|\varDelta _e| \beta _e \ll \beta _e^{2/7}$), the maximum growth rate of the EST instability can be estimated analytically. Adopting the orderings
$|\varDelta _e| \beta _e \ll \beta _e^{2/7}$), the maximum growth rate of the EST instability can be estimated analytically. Adopting the orderings
it can be shown (see Appendix K.3.11) that the EST mode has the growth rate
 \begin{align} \frac{\gamma}{\varOmega_e} = {\rm \pi}k_{\|} k_{\bot}^3 \rho_e^4 \left(|\varDelta_e| - \frac{k_{\bot}^2 \rho_e^2}{\beta_e}\right) \left\{1+\frac{{\rm \pi} k_{\bot}^2 \rho_e^2}{k_{\|}^2 \rho_e^2} \left[4 \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} +\sqrt{\rm \pi} \mu_e^{1/2} k_{\|}^3 \rho_e^3 \right]\right\}^{{-}1} , \end{align}
\begin{align} \frac{\gamma}{\varOmega_e} = {\rm \pi}k_{\|} k_{\bot}^3 \rho_e^4 \left(|\varDelta_e| - \frac{k_{\bot}^2 \rho_e^2}{\beta_e}\right) \left\{1+\frac{{\rm \pi} k_{\bot}^2 \rho_e^2}{k_{\|}^2 \rho_e^2} \left[4 \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} +\sqrt{\rm \pi} \mu_e^{1/2} k_{\|}^3 \rho_e^3 \right]\right\}^{{-}1} , \end{align}
where the term proportional to ![]() $\mu _e^{1/2}$ is associated with Landau damping on the ion species. Taking the subsidiary limit
$\mu _e^{1/2}$ is associated with Landau damping on the ion species. Taking the subsidiary limit ![]() $k_{\|} \rho _e \ll 1/\sqrt {\log {|\varDelta _e| \beta _e}}$, we recover (4.94). The EST mode's growth rate is, therefore, anticipated to be positive provided
$k_{\|} \rho _e \ll 1/\sqrt {\log {|\varDelta _e| \beta _e}}$, we recover (4.94). The EST mode's growth rate is, therefore, anticipated to be positive provided ![]() $k_{\bot } \rho _e < (|\varDelta _e| \beta _e)^{1/2}$. It can then be shown that (4.97) has the approximate maximum value
$k_{\bot } \rho _e < (|\varDelta _e| \beta _e)^{1/2}$. It can then be shown that (4.97) has the approximate maximum value
at the wavenumbers
 $$\begin{align} (k_{\bot} \rho_e)_{\mathrm{peak}} &= \left(\frac{3 |\varDelta_e| \beta_e}{5}\right)^{1/2} , \end{align}$$
$$\begin{align} (k_{\bot} \rho_e)_{\mathrm{peak}} &= \left(\frac{3 |\varDelta_e| \beta_e}{5}\right)^{1/2} , \end{align}$$The growth rate (4.97) is plotted in figure 27(b) along with the numerically determined growth rate; reasonable agreement is found.
We note that, for perpendicular wavenumbers ![]() $k_{\perp } \rho _e \gtrsim \beta _e^{1/7}$, the characteristic quasi-perpendicular plasma modes in a Maxwellian plasma are not EST modes, but are instead whisper waves (see § 4.4.10). Therefore, when
$k_{\perp } \rho _e \gtrsim \beta _e^{1/7}$, the characteristic quasi-perpendicular plasma modes in a Maxwellian plasma are not EST modes, but are instead whisper waves (see § 4.4.10). Therefore, when ![]() $|\varDelta _e| \beta _e \gtrsim \beta _e^{2/7}$ (see (4.106)), the expressions (4.98) and (4.99a) for the EST mode's maximum growth rate and the perpendicular wavenumber at which that growth is attained are no longer valid. Instead, when
$|\varDelta _e| \beta _e \gtrsim \beta _e^{2/7}$ (see (4.106)), the expressions (4.98) and (4.99a) for the EST mode's maximum growth rate and the perpendicular wavenumber at which that growth is attained are no longer valid. Instead, when ![]() $|\varDelta _e| \beta _e \gtrsim \beta _e^{2/7}$, the fastest-growing EST modes (which coexist with faster-growing unstable whisper waves) are those close to the scale
$|\varDelta _e| \beta _e \gtrsim \beta _e^{2/7}$, the fastest-growing EST modes (which coexist with faster-growing unstable whisper waves) are those close to the scale ![]() $k_{\perp } \rho _e \sim \varDelta _e^{-1/5}$; extrapolating from (4.97), we find that
$k_{\perp } \rho _e \sim \varDelta _e^{-1/5}$; extrapolating from (4.97), we find that ![]() $\gamma _{\rm max} \sim |\varDelta _e|^{2/5} \varOmega _e/\sqrt {\log {|\varDelta _e| \beta _e}}$.
$\gamma _{\rm max} \sim |\varDelta _e|^{2/5} \varOmega _e/\sqrt {\log {|\varDelta _e| \beta _e}}$.
4.4.9. Oblique transverse instability
The transverse instability (whose physical mechanism was discussed in § 4.3.3) can be excited for sufficiently large negative electron pressure anisotropies as well as positive ones; however, when ![]() $\varDelta _e < 0$, the fastest-growing modes are highly oblique with respect to the background magnetic field as opposed to parallel to it. In contrast to the
$\varDelta _e < 0$, the fastest-growing modes are highly oblique with respect to the background magnetic field as opposed to parallel to it. In contrast to the ![]() $\varDelta _e > 0$ case, the oblique transverse instability does not become the fastest-growing CES microinstability for all
$\varDelta _e > 0$ case, the oblique transverse instability does not become the fastest-growing CES microinstability for all ![]() $\varDelta _e \ll -\beta _e^{-1}$, only becoming so once its maximum growth rate exceeds the electron-Larmor frequency (which occurs when
$\varDelta _e \ll -\beta _e^{-1}$, only becoming so once its maximum growth rate exceeds the electron-Larmor frequency (which occurs when ![]() $\varDelta _e \lesssim -\beta _e^{-1/3}$). While
$\varDelta _e \lesssim -\beta _e^{-1/3}$). While ![]() $\varDelta _e > -\beta _e^{-1/3}$, the fastest-growing oblique transverse modes, which have
$\varDelta _e > -\beta _e^{-1/3}$, the fastest-growing oblique transverse modes, which have ![]() $k_{\perp } \rho _e \sim (|\varDelta _e| \beta _e)^{1/2}$, are confined to the parallel wavenumbers satisfying
$k_{\perp } \rho _e \sim (|\varDelta _e| \beta _e)^{1/2}$, are confined to the parallel wavenumbers satisfying ![]() $k_{\|} \rho _e \gtrsim 1$. Their growth is outcompeted by the EST and whisper instabilities (see §§ 4.4.8 and 4.4.10, respectively), which have
$k_{\|} \rho _e \gtrsim 1$. Their growth is outcompeted by the EST and whisper instabilities (see §§ 4.4.8 and 4.4.10, respectively), which have ![]() $k_{\|} \rho _e < 1$; this is illustrated numerically in figure 28(a) for a particular large, negative value of
$k_{\|} \rho _e < 1$; this is illustrated numerically in figure 28(a) for a particular large, negative value of ![]() $\varDelta _e \beta _e$.
$\varDelta _e \beta _e$.

Figure 28. The CES oblique transverse instability. (a) Maximum positive growth rates of linear perturbations resulting from CE ion- and electron-shear terms in the CE distribution function (4.1) for ![]() $\varDelta _e \beta = -100$ and
$\varDelta _e \beta = -100$ and ![]() $\beta _e = 10^4$. Here, a temperature-equilibrated hydrogen plasma is considered viz.
$\beta _e = 10^4$. Here, a temperature-equilibrated hydrogen plasma is considered viz. ![]() $\varDelta _e = \mu _e^{1/2} \varDelta _i$, and
$\varDelta _e = \mu _e^{1/2} \varDelta _i$, and ![]() $\beta _i = \beta _e$. The growth rates of all modes are calculated in the same way as figure 25. (b) Plot of the oblique transverse mode's growth rate (solid line) as a function of
$\beta _i = \beta _e$. The growth rates of all modes are calculated in the same way as figure 25. (b) Plot of the oblique transverse mode's growth rate (solid line) as a function of ![]() $k_{\|} \rho _e$ with
$k_{\|} \rho _e$ with ![]() $k_{\bot } \rho _e = (|\varDelta _e|\beta _e/3)^{1/2}$ (top), and as a function of
$k_{\bot } \rho _e = (|\varDelta _e|\beta _e/3)^{1/2}$ (top), and as a function of ![]() $k_{\perp } \rho _e$ with
$k_{\perp } \rho _e$ with ![]() $k_{\|} \rho _e = 2$ (bottom). The dotted and dashed lines show the analytical prediction (4.97).
$k_{\|} \rho _e = 2$ (bottom). The dotted and dashed lines show the analytical prediction (4.97).
As for their analytical characterisation, transverse modes have identical growth rates to those obtained in the ![]() $\varDelta _e > 0$ case, given by (4.29a,b). For
$\varDelta _e > 0$ case, given by (4.29a,b). For ![]() $\varDelta _e < 0$, only the first mode can have positive growth, and such growth is only realised if
$\varDelta _e < 0$, only the first mode can have positive growth, and such growth is only realised if ![]() $k_{\bot } > k_{\|}$. Now taking the quasi-perpendicular unmagnetised limit
$k_{\bot } > k_{\|}$. Now taking the quasi-perpendicular unmagnetised limit ![]() $k_{\bot } \rho _e \gg k_{\|} \rho _e \gg 1$, we find that this mode has the growth rate
$k_{\bot } \rho _e \gg k_{\|} \rho _e \gg 1$, we find that this mode has the growth rate
This expression is mathematically identical to the parallel transverse instability (4.30) (§ 4.3.3), except with substitution ![]() $k_{\|} \rightarrow k_{\bot }$; the maximum growth rate of the oblique transverse instability is, therefore,
$k_{\|} \rightarrow k_{\bot }$; the maximum growth rate of the oblique transverse instability is, therefore,
at the (perpendicular) wavenumber
 \begin{equation} (k_{\bot}
\rho_e)_{\mathrm{peak}} = \left(\frac{\varDelta_e \beta_e}{3}\right)^{1/2} .
\end{equation}
\begin{equation} (k_{\bot}
\rho_e)_{\mathrm{peak}} = \left(\frac{\varDelta_e \beta_e}{3}\right)^{1/2} .
\end{equation}
(4.100) is compared with the numerically determined growth rate in figure 28(b); we find that the approximation is excellent provided ![]() $k_{\|} \rho _e \gtrsim 1$.
$k_{\|} \rho _e \gtrsim 1$.
We note that, based on our analysis, the oblique transverse mode is anticipated always to have a smaller growth rate than the EST instability (4.98) when ![]() $1 \ll |\varDelta _e| \beta _e \lesssim \beta _e^{2/7}$:
$1 \ll |\varDelta _e| \beta _e \lesssim \beta _e^{2/7}$:
4.4.10. Whisper instability
When ![]() $\varDelta _e \lesssim -\beta _e^{-5/7}$ (but
$\varDelta _e \lesssim -\beta _e^{-5/7}$ (but ![]() $\varDelta _e \gg -\beta _e^{-1/3}$), the dominant CES microinstability is the CES whisper instability. The instability is so named, because it consists in the destabilisation of the whisper wave, a plasma wave whose existence has not previously been identified: it is therefore of some interest.Footnote 8 The likely reason for its previous neglect relates to the somewhat esoteric regime in which such a wave exists – a magnetised plasma with
$\varDelta _e \gg -\beta _e^{-1/3}$), the dominant CES microinstability is the CES whisper instability. The instability is so named, because it consists in the destabilisation of the whisper wave, a plasma wave whose existence has not previously been identified: it is therefore of some interest.Footnote 8 The likely reason for its previous neglect relates to the somewhat esoteric regime in which such a wave exists – a magnetised plasma with ![]() $\beta _e \gg 1$ that might naively be expected to support essentially unmagnetised perturbations at
$\beta _e \gg 1$ that might naively be expected to support essentially unmagnetised perturbations at ![]() $k \rho _e \gg 1$. The energetically dominant magnetic component of the wave is perpendicular to both
$k \rho _e \gg 1$. The energetically dominant magnetic component of the wave is perpendicular to both ![]() $\boldsymbol {k}$ and
$\boldsymbol {k}$ and ![]() $\boldsymbol {B}_0$ (viz.
$\boldsymbol {B}_0$ (viz. ![]() $\delta B_y$), and the wave itself has no electron-number-density perturbation unless
$\delta B_y$), and the wave itself has no electron-number-density perturbation unless ![]() $\beta _e$ is extremely large. Its operation (and also the operation of its instability in a CE plasma) involves both resonant and non-resonant interactions between electrons and the wave. More specifically, it is the non-resonant interaction of electrons at the edge of their Larmor orbits with the parallel electric field associated with the whisper wave that gives rise to the phase-shifted current perturbation necessary for wave propagation, while the primary damping mechanisms (Landau and Barnes’ damping, respectively) of whisper waves are mediated by resonant wave–particle interactions. The physical mechanism of this wave and its instability (which is most clearly explored within the quasi-perpendicular limit of gyrokinetics) will be discussed further in a future paper.
$\beta _e$ is extremely large. Its operation (and also the operation of its instability in a CE plasma) involves both resonant and non-resonant interactions between electrons and the wave. More specifically, it is the non-resonant interaction of electrons at the edge of their Larmor orbits with the parallel electric field associated with the whisper wave that gives rise to the phase-shifted current perturbation necessary for wave propagation, while the primary damping mechanisms (Landau and Barnes’ damping, respectively) of whisper waves are mediated by resonant wave–particle interactions. The physical mechanism of this wave and its instability (which is most clearly explored within the quasi-perpendicular limit of gyrokinetics) will be discussed further in a future paper.
We characterise the whisper instability's growth analytically in the limits ![]() $\mu _e^{1/2} \ll k_{\|} \rho _e \ll 1$,
$\mu _e^{1/2} \ll k_{\|} \rho _e \ll 1$, ![]() $k_{\bot } \rho _e \gg 1$ and
$k_{\bot } \rho _e \gg 1$ and ![]() $\varDelta _e \beta _e \gg 1$ under the orderings
$\varDelta _e \beta _e \gg 1$ under the orderings
It can be shown (see Appendix K.3.12) that such modes have complex frequencies
 \begin{align} \frac{\omega}{\varOmega_e} & ={-}\mathrm{i} \left[\frac{\sqrt{\rm \pi}}{2 k_{\|} \rho_e} \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} + \frac{k_{\|} \rho_e}{8 \sqrt{\rm \pi} k_{\bot}^2 \rho_e^2}\right] \nonumber\\ &\quad \pm k_{\|} \rho_e \sqrt{\frac{\sqrt{\rm \pi}}{4} k_{\bot} \rho_e \left(\frac{k_{\bot}^2 \rho_e^2}{\beta_e}+\varDelta_e \right) - \left[\frac{\sqrt{\rm \pi}}{2 k_{\|}^2 \rho_e^2} \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} + \frac{1}{8 \sqrt{\rm \pi} k_{\bot}^2 \rho_e^2} \right]^2} . \end{align}
\begin{align} \frac{\omega}{\varOmega_e} & ={-}\mathrm{i} \left[\frac{\sqrt{\rm \pi}}{2 k_{\|} \rho_e} \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} + \frac{k_{\|} \rho_e}{8 \sqrt{\rm \pi} k_{\bot}^2 \rho_e^2}\right] \nonumber\\ &\quad \pm k_{\|} \rho_e \sqrt{\frac{\sqrt{\rm \pi}}{4} k_{\bot} \rho_e \left(\frac{k_{\bot}^2 \rho_e^2}{\beta_e}+\varDelta_e \right) - \left[\frac{\sqrt{\rm \pi}}{2 k_{\|}^2 \rho_e^2} \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} + \frac{1}{8 \sqrt{\rm \pi} k_{\bot}^2 \rho_e^2} \right]^2} . \end{align}
It is a simple matter to ascertain that the right-hand side of (4.105) is either purely real or purely imaginary, and thus modes are approximately either non-propagating with growth rate ![]() $\gamma$ or purely oscillating with frequency
$\gamma$ or purely oscillating with frequency ![]() $\varpi$. The dispersion curves
$\varpi$. The dispersion curves ![]() $\varpi (k_\perp )$ and
$\varpi (k_\perp )$ and ![]() $\gamma (k_\perp )$ are plotted in figure 29. To interpret (4.105), we take subsidiary limits.
$\gamma (k_\perp )$ are plotted in figure 29. To interpret (4.105), we take subsidiary limits.

Figure 29. The CES EST vs whisper instability. Growth rates of EST and whisper modes whose instability is driven by the CE electron-shear term in the CE distribution function (4.1), for quasi-perpendicular (![]() $k_{\|} \ll k_{\perp }$) wavevectors with respect to the background magnetic field. The growth rates (solid lines) of all modes are calculated in the same way as figure 25 for a selection of different values of
$k_{\|} \ll k_{\perp }$) wavevectors with respect to the background magnetic field. The growth rates (solid lines) of all modes are calculated in the same way as figure 25 for a selection of different values of ![]() $\varDelta _e \beta _e$ and
$\varDelta _e \beta _e$ and ![]() $\beta _e$, and
$\beta _e$, and ![]() $k_{\|} \rho _e = 0.35$. The approximations (4.97), (4.105), and (4.109) for the real frequency (dotted, dot-dashed and dashed blue, respectively) and growth rate (dotted, dot-dashed and dashed red, respectively) in the limit
$k_{\|} \rho _e = 0.35$. The approximations (4.97), (4.105), and (4.109) for the real frequency (dotted, dot-dashed and dashed blue, respectively) and growth rate (dotted, dot-dashed and dashed red, respectively) in the limit ![]() $k_{\|} \rho _e \ll 1$,
$k_{\|} \rho _e \ll 1$, ![]() $k_{\perp } \rho _e \gg 1$, are also plotted.
$k_{\perp } \rho _e \gg 1$, are also plotted.
We first consider ![]() $1 \ll k_{\bot } \rho _e \sim (|\varDelta _e| \beta _e)^{1/2} \ll \beta _e^{1/7}$. In this case, the second term in the square root is much larger than the first, so the expression for the ‘
$1 \ll k_{\bot } \rho _e \sim (|\varDelta _e| \beta _e)^{1/2} \ll \beta _e^{1/7}$. In this case, the second term in the square root is much larger than the first, so the expression for the ‘![]() $+$’ root simplifies to the dispersion relation (4.97) of the EST instability. However, when the perpendicular wavenumber (4.99a) of the EST instability's peak growth derived from (4.97) exceeds
$+$’ root simplifies to the dispersion relation (4.97) of the EST instability. However, when the perpendicular wavenumber (4.99a) of the EST instability's peak growth derived from (4.97) exceeds ![]() $(k_\perp \rho _e)_{\rm peak} \gtrsim 3^{1/7} 2^{-5/7} {\rm \pi}^{-3/14} \beta _e^{1/7} \approx 0.56 \beta _e^{1/7}$, this simplification is no longer justifiable. Therefore, when so when
$(k_\perp \rho _e)_{\rm peak} \gtrsim 3^{1/7} 2^{-5/7} {\rm \pi}^{-3/14} \beta _e^{1/7} \approx 0.56 \beta _e^{1/7}$, this simplification is no longer justifiable. Therefore, when so when
(4.97) is no longer, in fact, a valid description of the EST mode's growth rate.
Now considering the subsidiary limit ![]() $k_{\perp } \rho _e \sim (|\varDelta _e| \beta _e)^{1/2} \gg \beta _e^{1/7}$ and
$k_{\perp } \rho _e \sim (|\varDelta _e| \beta _e)^{1/2} \gg \beta _e^{1/7}$ and ![]() $k_{\|} \rho _e \ll 1/\sqrt {\log {|\varDelta _e| \beta _e}}$ of (4.105), we find two propagating modes:
$k_{\|} \rho _e \ll 1/\sqrt {\log {|\varDelta _e| \beta _e}}$ of (4.105), we find two propagating modes:
 \begin{equation} \frac{\omega}{\varOmega_e} \approx{\pm} \frac{{\rm \pi}^{1/4}}{2} k_{\|} \rho_e \sqrt{k_{\bot} \rho_e \left(\frac{k_{\bot}^2 \rho_e^2}{\beta_e}+\varDelta_e \right)} . \end{equation}
\begin{equation} \frac{\omega}{\varOmega_e} \approx{\pm} \frac{{\rm \pi}^{1/4}}{2} k_{\|} \rho_e \sqrt{k_{\bot} \rho_e \left(\frac{k_{\bot}^2 \rho_e^2}{\beta_e}+\varDelta_e \right)} . \end{equation}
If we set ![]() $\varDelta _e = 0$ in order to identify the underlying Maxwellian mode, this reduces to
$\varDelta _e = 0$ in order to identify the underlying Maxwellian mode, this reduces to
 \begin{equation} \frac{\omega}{\varOmega_e} \approx{\pm} \frac{{\rm \pi}^{1/4}}{2} k_{\|} \rho_e \frac{(k_{\bot} \rho_e)^{3/2}}{\beta_e^{1/2}} . \end{equation}
\begin{equation} \frac{\omega}{\varOmega_e} \approx{\pm} \frac{{\rm \pi}^{1/4}}{2} k_{\|} \rho_e \frac{(k_{\bot} \rho_e)^{3/2}}{\beta_e^{1/2}} . \end{equation}This dispersion relation, which does not coincide with any previously identified plasma wave, is that of the whisper wave.
The presence of this wave in the case of ![]() $\varDelta _e < 0$ results in a purely unstable mode provided
$\varDelta _e < 0$ results in a purely unstable mode provided ![]() $\beta _e^{-1/7} \ll k_{\bot } \rho _e < (|\varDelta _e| \beta _e)^{1/2}$ and retaining finite
$\beta _e^{-1/7} \ll k_{\bot } \rho _e < (|\varDelta _e| \beta _e)^{1/2}$ and retaining finite ![]() $k_{\|} \rho _e$. In this subsidiary limit, the growth rate of the instability is
$k_{\|} \rho _e$. In this subsidiary limit, the growth rate of the instability is
 \begin{align} \frac{\gamma}{\varOmega_e} & ={-} \frac{\sqrt{\rm \pi}}{2 k_{\|} \rho_e} \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} \nonumber\\ &\quad \pm k_{\|} \rho_e \sqrt{\frac{\sqrt{\rm \pi}}{4} k_{\bot} \rho_e \left(|\varDelta_e| - \frac{k_{\bot}^2 \rho_e^2}{\beta_e}\right) + \frac{\rm \pi}{2 k_{\|}^4 \rho_e^4} \exp{\left(-\frac{2}{k_{\|}^2 \rho_e^2}\right)}} . \end{align}
\begin{align} \frac{\gamma}{\varOmega_e} & ={-} \frac{\sqrt{\rm \pi}}{2 k_{\|} \rho_e} \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} \nonumber\\ &\quad \pm k_{\|} \rho_e \sqrt{\frac{\sqrt{\rm \pi}}{4} k_{\bot} \rho_e \left(|\varDelta_e| - \frac{k_{\bot}^2 \rho_e^2}{\beta_e}\right) + \frac{\rm \pi}{2 k_{\|}^4 \rho_e^4} \exp{\left(-\frac{2}{k_{\|}^2 \rho_e^2}\right)}} . \end{align}This has the maximum value
at the wavenumbers
 $$\begin{align} (k_{\bot} \rho_e)_{\mathrm{peak}} &= \left(\frac{|\varDelta_e| \beta_e}{3}\right)^{1/2} , \end{align}$$
$$\begin{align} (k_{\bot} \rho_e)_{\mathrm{peak}} &= \left(\frac{|\varDelta_e| \beta_e}{3}\right)^{1/2} , \end{align}$$ Thus, the maximum growth rate of whisper instability has different scalings with ![]() $|\varDelta _e|$ and
$|\varDelta _e|$ and ![]() $\beta _e$ than either the EST instability (4.98) or the oblique transverse instability (4.101). When
$\beta _e$ than either the EST instability (4.98) or the oblique transverse instability (4.101). When ![]() $|\varDelta _e| \beta _e \gtrsim \beta _e^{2/7}$, (4.105) implies that the growth rate
$|\varDelta _e| \beta _e \gtrsim \beta _e^{2/7}$, (4.105) implies that the growth rate ![]() $\gamma$ continues to increase beyond the maximum value of
$\gamma$ continues to increase beyond the maximum value of ![]() $k_\perp \rho _e$ at which the EST modes can exist, and thus the whisper instability, if it is operating, is always dominant over the EST instability. Whether it is also dominant over the oblique transverse instability depends on the choice of
$k_\perp \rho _e$ at which the EST modes can exist, and thus the whisper instability, if it is operating, is always dominant over the EST instability. Whether it is also dominant over the oblique transverse instability depends on the choice of ![]() $\beta _e$ and
$\beta _e$ and ![]() $\varDelta _e$. We can quantify this explicitly, by considering the ratio of the oblique transverse instability's growth rate (4.101) to that of the whisper instability
$\varDelta _e$. We can quantify this explicitly, by considering the ratio of the oblique transverse instability's growth rate (4.101) to that of the whisper instability
We see that for ![]() $|\varDelta _e|^3 \beta _e \ll 1$,
$|\varDelta _e|^3 \beta _e \ll 1$, ![]() $\gamma _{\rm trans} \ll \gamma _{\rm whisper}$. Thus for
$\gamma _{\rm trans} \ll \gamma _{\rm whisper}$. Thus for ![]() $|\varDelta _e|^{-7/5} \ll \beta _e \ll |\varDelta _e|^{-3}$, the whisper instability dominates. This condition certainly holds for the particular value of
$|\varDelta _e|^{-7/5} \ll \beta _e \ll |\varDelta _e|^{-3}$, the whisper instability dominates. This condition certainly holds for the particular value of ![]() $\varDelta _e$ considered in figure 28; to support our claim, in figure 30(a) we plot the analytical approximation (4.109) along with the numerically determined growth rate for the fixed values of
$\varDelta _e$ considered in figure 28; to support our claim, in figure 30(a) we plot the analytical approximation (4.109) along with the numerically determined growth rate for the fixed values of ![]() $k_{\perp } \rho _e$ and
$k_{\perp } \rho _e$ and ![]() $k_{\|} \rho _e$, respectively, at which the whisper instability is predicted to achieve its maximum growth. The growth rate of the whisper instability, which is correctly captured by our analytic approximation, does indeed exceed that of the transverse instability by an appreciable factor.
$k_{\|} \rho _e$, respectively, at which the whisper instability is predicted to achieve its maximum growth. The growth rate of the whisper instability, which is correctly captured by our analytic approximation, does indeed exceed that of the transverse instability by an appreciable factor.

Figure 30. The CES whisper instability. (a) Plot of the whisper instability's growth rate as a function of ![]() $k_{\|} \rho _e$ with
$k_{\|} \rho _e$ with ![]() $k_{\bot } \rho _e = (|\varDelta _e|\beta _e/3)^{1/2}$ (top), and as a function of
$k_{\bot } \rho _e = (|\varDelta _e|\beta _e/3)^{1/2}$ (top), and as a function of ![]() $k_{\perp } \rho _e$ with
$k_{\perp } \rho _e$ with ![]() $k_{\|} \rho _e = (k_{\|} \rho _e)_{\rm peak}$ (bottom), where
$k_{\|} \rho _e = (k_{\|} \rho _e)_{\rm peak}$ (bottom), where ![]() $(k_{\|} \rho _e)_{\rm peak}$ is given by (4.111b), for
$(k_{\|} \rho _e)_{\rm peak}$ is given by (4.111b), for ![]() $\varDelta _e \beta = -100$ and
$\varDelta _e \beta = -100$ and ![]() $\beta _e = 10^4$ (cf. figure (28)). The numerically determined value of this quantity is calculated in the same way as figure 25. The dotted and dashed lines show the analytical prediction (4.109). (b) Divergence of growth rates (dotted lines) arising from using the approach outlined in Appendix K (which involves solving a simplified ‘low-frequency’ dispersion relation) as compared with the full hot-plasma dispersion relation (dashed lines) when
$\beta _e = 10^4$ (cf. figure (28)). The numerically determined value of this quantity is calculated in the same way as figure 25. The dotted and dashed lines show the analytical prediction (4.109). (b) Divergence of growth rates (dotted lines) arising from using the approach outlined in Appendix K (which involves solving a simplified ‘low-frequency’ dispersion relation) as compared with the full hot-plasma dispersion relation (dashed lines) when ![]() $\beta _e \sim |\varDelta _e|^{-3}$. Here,
$\beta _e \sim |\varDelta _e|^{-3}$. Here, ![]() $\varDelta _e = -0.01$,
$\varDelta _e = -0.01$, ![]() $k_{\bot } \rho _e = (|\varDelta _e| \beta _e/3)^{1/2}$ and
$k_{\bot } \rho _e = (|\varDelta _e| \beta _e/3)^{1/2}$ and ![]() $\beta _e$ is varied. For reference,
$\beta _e$ is varied. For reference, ![]() $\beta _e = 0.01 |\varDelta _e|^{-3} = 10^{4}$ corresponds to the same values of
$\beta _e = 0.01 |\varDelta _e|^{-3} = 10^{4}$ corresponds to the same values of ![]() $\beta _e$ and
$\beta _e$ and ![]() $\varDelta _e$ as considered in figure 28.
$\varDelta _e$ as considered in figure 28.
For ![]() $\beta _e \gtrsim |\varDelta _e|^{-3}$, (4.110) implies that, in fact,
$\beta _e \gtrsim |\varDelta _e|^{-3}$, (4.110) implies that, in fact, ![]() $\gamma /k_{\|} v_{\mathrm {th}e} \sim 1$. This violates the condition of validity of the method that we have generally used to evaluate CES microinstability growth rates numerically (see § 2.5.8, and also Appendix K). The divergence of the true growth rates (calculated by solving the full hot-plasma dispersion relation numerically) from those arising from the solution of the low-frequency (
$\gamma /k_{\|} v_{\mathrm {th}e} \sim 1$. This violates the condition of validity of the method that we have generally used to evaluate CES microinstability growth rates numerically (see § 2.5.8, and also Appendix K). The divergence of the true growth rates (calculated by solving the full hot-plasma dispersion relation numerically) from those arising from the solution of the low-frequency (![]() $\omega \ll k_{\|} v_{\mathrm {th}e}$) dispersion relation (K23) for increasing
$\omega \ll k_{\|} v_{\mathrm {th}e}$) dispersion relation (K23) for increasing ![]() $\beta _e$ is illustrated in figure 30(b). For
$\beta _e$ is illustrated in figure 30(b). For ![]() $\gamma \gtrsim \varOmega _e$, we find that the distinction between
$\gamma \gtrsim \varOmega _e$, we find that the distinction between ![]() $k_{\|} \rho _e < 1$ modes and
$k_{\|} \rho _e < 1$ modes and ![]() $k_{\|} \rho _e > 1$ modes vanishes; furthermore, the fastest-growing modes (including the modes with
$k_{\|} \rho _e > 1$ modes vanishes; furthermore, the fastest-growing modes (including the modes with ![]() $k_{\|} = 0$) come to resemble the transverse instability when
$k_{\|} = 0$) come to resemble the transverse instability when ![]() $\beta _e \gg |\varDelta _e|^{-3}$; this feature, which indicates the emergence of yet another distinct CES instability, is discussed in the next section.
$\beta _e \gg |\varDelta _e|^{-3}$; this feature, which indicates the emergence of yet another distinct CES instability, is discussed in the next section.
4.4.11. Ordinary-mode instability
The final instability we consider in this paper is the CES ordinary-mode (electromagnetic) instability: the destabilisation of the ordinary mode at sub-electron-Larmor scales by negative electron-pressure anisotropy. The bi-Maxwellian equivalent of the instability was first identified by Davidson & Wu (Reference Davidson and Wu1970); for a more recent linear study of the instability, see Ibscher et al. (Reference Ibscher, Lazar and Schlickeiser2012). For the characteristically small electron-pressure anisotropies that are associated with the CE electron-shear term, this instability can only arise at very large values of ![]() $\beta _e$. For purely perpendicular modes (
$\beta _e$. For purely perpendicular modes (![]() $k_{\|} = 0$) in a magnetised plasma, resonant wave–particle interactions cannot arise, and so the ordinary-mode's instability mechanism is non-resonant.
$k_{\|} = 0$) in a magnetised plasma, resonant wave–particle interactions cannot arise, and so the ordinary-mode's instability mechanism is non-resonant.
The CES ordinary-mode instability is most simply characterised by considering modes that are exactly perpendicular to the guide magnetic field (viz. ![]() $k_{\|} = 0$). In this case, it can be shown (see Appendix K.3.13) that, if the ordinary mode is destabilised, its growth rate is given by the equation
$k_{\|} = 0$). In this case, it can be shown (see Appendix K.3.13) that, if the ordinary mode is destabilised, its growth rate is given by the equation
 \begin{align} \sum_{n = 1}^{\infty} \frac{2 \gamma^2}{\gamma^2+n^2 \varOmega_e^2} \exp \left(-\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) ={-}\varDelta_e- k_{\bot}^2 d_e^2 - \exp \left(-\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) . \end{align}
\begin{align} \sum_{n = 1}^{\infty} \frac{2 \gamma^2}{\gamma^2+n^2 \varOmega_e^2} \exp \left(-\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) ={-}\varDelta_e- k_{\bot}^2 d_e^2 - \exp \left(-\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) . \end{align}This dispersion relation is very similar to that derived by Davidson & Wu (Reference Davidson and Wu1970) for the ordinary-mode instability in the case of a bi-Maxwellian distribution. If the electron-pressure anisotropy is insufficient to destabilise the ordinary mode, the mode is undamped, and its real frequency satisfies
 \begin{align} \sum_{n = 1}^{\infty} \frac{2 \varpi^2}{n^2 \varOmega_e^2-\varpi^2} \exp \left(-\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) = \varDelta_e+ k_{\bot}^2 d_e^2 + \exp \left(-\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) . \end{align}
\begin{align} \sum_{n = 1}^{\infty} \frac{2 \varpi^2}{n^2 \varOmega_e^2-\varpi^2} \exp \left(-\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) = \varDelta_e+ k_{\bot}^2 d_e^2 + \exp \left(-\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \rho_{e}^2}{2}\right) . \end{align}
The dispersion curves ![]() $\varpi (k_{\perp })$ and
$\varpi (k_{\perp })$ and ![]() $\gamma (k_{\perp })$ for a selection of different values of
$\gamma (k_{\perp })$ for a selection of different values of ![]() $\beta _e$ and at fixed
$\beta _e$ and at fixed ![]() $\varDelta _e$ are shown in figure 31.
$\varDelta _e$ are shown in figure 31.

Figure 31. The CES ordinary-mode instability. Growth rates of ordinary modes whose instability is driven by the CE electron-shear term in the CE distribution function (4.1), for perpendicular (![]() $k_{\|} = 0$) wavevectors with respect to the background magnetic field. The growth rates (solid lines) of the modes are calculated using (4.113) and (4.114). We show the growth rates for a selection of different values of
$k_{\|} = 0$) wavevectors with respect to the background magnetic field. The growth rates (solid lines) of the modes are calculated using (4.113) and (4.114). We show the growth rates for a selection of different values of ![]() $\beta _e$ and for
$\beta _e$ and for ![]() $\varDelta _e = 0.01$. The approximation (4.121) of the growth rate in the limit
$\varDelta _e = 0.01$. The approximation (4.121) of the growth rate in the limit ![]() $k_{\perp } \rho _e \gg \gamma /\varOmega _e \gg 1$ is also plotted (dashed red).
$k_{\perp } \rho _e \gg \gamma /\varOmega _e \gg 1$ is also plotted (dashed red).
We can use the ordinary-mode dispersion relation (4.113) to derive the threshold for this instability at exactly perpendicular wavevectors. We note that the left-hand side of (4.113) is strictly positive; thus for solutions to exist, it is required that there exist a range of perpendicular wavenumbers over which the right-hand side of (4.113) is also positive. For ![]() $k_{\bot } \rho _e \lesssim 1$, the right-hand side is always negative because
$k_{\bot } \rho _e \lesssim 1$, the right-hand side is always negative because ![]() $|\varDelta _e| \ll 1$. We therefore consider the limit
$|\varDelta _e| \ll 1$. We therefore consider the limit ![]() $k_{\bot } \rho _e \gg 1$ (assuming
$k_{\bot } \rho _e \gg 1$ (assuming ![]() $\gamma \sim \varOmega _e$), for which
$\gamma \sim \varOmega _e$), for which
 \begin{equation} \frac{1}{\sqrt{\rm \pi} k_{\bot} \rho_e} \sum_{n = 1}^{\infty} \frac{2 \gamma^2}{\gamma^2+n^2 \varOmega_e^2} \approx |\varDelta_e|- \frac{k_{\bot}^2 \rho_e^2}{\beta_e} - \frac{1}{\sqrt{\rm \pi} k_{\bot} \rho_e} . \end{equation}
\begin{equation} \frac{1}{\sqrt{\rm \pi} k_{\bot} \rho_e} \sum_{n = 1}^{\infty} \frac{2 \gamma^2}{\gamma^2+n^2 \varOmega_e^2} \approx |\varDelta_e|- \frac{k_{\bot}^2 \rho_e^2}{\beta_e} - \frac{1}{\sqrt{\rm \pi} k_{\bot} \rho_e} . \end{equation}The right-hand side of (4.115) is maximal when
 \begin{equation} k_{\bot} \rho_e = \left(\frac{\beta_e}{2\sqrt{\rm \pi}}\right)^{1/3} , \end{equation}
\begin{equation} k_{\bot} \rho_e = \left(\frac{\beta_e}{2\sqrt{\rm \pi}}\right)^{1/3} , \end{equation}and, when maximal, also greater than zero if and only if
Therefore the threshold (4.117) is a necessary condition for a purely perpendicular instability to exist. It is also a sufficient condition, because the left-hand side of (4.115) becomes arbitrarily small for small ![]() $\gamma$. Comparing the threshold (4.117) with figure 30(b), we conclude that the emergence of an instability with a purely perpendicular wavenumber at around
$\gamma$. Comparing the threshold (4.117) with figure 30(b), we conclude that the emergence of an instability with a purely perpendicular wavenumber at around ![]() $\beta _e \sim |\varDelta _e|^{-3}$ is consistent with numerical expectations. In the limit
$\beta _e \sim |\varDelta _e|^{-3}$ is consistent with numerical expectations. In the limit ![]() $\beta _e \gg \varDelta _e^{-3}$, all modes whose perpendicular wavenumbers satisfy
$\beta _e \gg \varDelta _e^{-3}$, all modes whose perpendicular wavenumbers satisfy
are unstable.
One can also show analytically that for ![]() $\gamma \gg \varOmega _e$, these unstable ordinary modes grow at the same rate as unstable oblique transverse modes (§ 4.4.9). Motivated by the fact that
$\gamma \gg \varOmega _e$, these unstable ordinary modes grow at the same rate as unstable oblique transverse modes (§ 4.4.9). Motivated by the fact that ![]() $\gamma \ll k_{\bot } v_{\mathrm {th}e}$ for the oblique transverse instability, or, equivalently,
$\gamma \ll k_{\bot } v_{\mathrm {th}e}$ for the oblique transverse instability, or, equivalently, ![]() $\gamma /\varOmega _e \ll k_{\bot } \rho _e$, we first consider (4.113) in the limit
$\gamma /\varOmega _e \ll k_{\bot } \rho _e$, we first consider (4.113) in the limit ![]() $k_{\bot } \rho _e \gg \gamma /\varOmega _e \sim 1$; we will subsequently take the subsidiary limit
$k_{\bot } \rho _e \gg \gamma /\varOmega _e \sim 1$; we will subsequently take the subsidiary limit ![]() $\gamma /\varOmega _e \gg 1$. The relevant dispersion relation is (4.115), which can be rewritten as
$\gamma /\varOmega _e \gg 1$. The relevant dispersion relation is (4.115), which can be rewritten as
using the summation identity
 \begin{equation} \sum_{n = 1}^{\infty} \frac{2 \gamma^2}{\gamma^2+n^2 \varOmega_e^2} = \frac{\gamma {\rm \pi}}{\varOmega_e} \coth{\left(\frac{\gamma {\rm \pi}}{\varOmega_e} \right)} - 1 . \end{equation}
\begin{equation} \sum_{n = 1}^{\infty} \frac{2 \gamma^2}{\gamma^2+n^2 \varOmega_e^2} = \frac{\gamma {\rm \pi}}{\varOmega_e} \coth{\left(\frac{\gamma {\rm \pi}}{\varOmega_e} \right)} - 1 . \end{equation}
Now assuming ![]() $\gamma \gg \varOmega _e$ and using
$\gamma \gg \varOmega _e$ and using ![]() $\coth {x} \approx 1$ for any number
$\coth {x} \approx 1$ for any number ![]() $x \gg 1$, we deduce
$x \gg 1$, we deduce
which is equivalent to (4.100). Since ![]() $|\varDelta _e| \ll 1$, our result is consistent with our initial assumption
$|\varDelta _e| \ll 1$, our result is consistent with our initial assumption ![]() $\gamma /\varOmega _e \ll k_{\bot } \rho _e$. We note that, at wavenumbers that do not satisfy (4.118), ordinary modes and oblique transverse modes behave quite differently: such ordinary modes have real frequencies and are neither growing nor damped, whereas transverse modes remain non-propagating.
$\gamma /\varOmega _e \ll k_{\bot } \rho _e$. We note that, at wavenumbers that do not satisfy (4.118), ordinary modes and oblique transverse modes behave quite differently: such ordinary modes have real frequencies and are neither growing nor damped, whereas transverse modes remain non-propagating.
In summary, we conclude that, when ![]() $\beta _e \gg |\varDelta _e|^{-3}$, the CES ordinary-mode instability is the dominant CES microinstability, but that in this limit, the fastest growing unstable modes are essentially identical to the unstable unmagnetised oblique transverse modes already described in § 4.4.9.
$\beta _e \gg |\varDelta _e|^{-3}$, the CES ordinary-mode instability is the dominant CES microinstability, but that in this limit, the fastest growing unstable modes are essentially identical to the unstable unmagnetised oblique transverse modes already described in § 4.4.9.
5. Discussion and conclusions
In this paper, we have shown that the CE description of classical, collisional plasma is valid for a wide range of plasma conditions. Microinstabilities are stabilised in such plasmas by two effects: collisional damping of instabilities, or ![]() $\beta$-dependent thresholds arising from a non-zero macroscopic magnetic field. In particular, we have demonstrated that predictions for transport based on the CE theory should not fail on account of kinetic instabilities in a collisional plasma whose constituent ions and electrons are strongly magnetised and that has
$\beta$-dependent thresholds arising from a non-zero macroscopic magnetic field. In particular, we have demonstrated that predictions for transport based on the CE theory should not fail on account of kinetic instabilities in a collisional plasma whose constituent ions and electrons are strongly magnetised and that has ![]() $\beta \lesssim 1$. By identifying the stable region for the leading-order corrections in the CE expansion, we have de facto identified the stable region for corrections to arbitrary order: if one of the above effects is enough to maintain stability, any perturbations arising from smaller corrections will be unable to overcome the same effect. However, we have also demonstrated that for plasmas with
$\beta \lesssim 1$. By identifying the stable region for the leading-order corrections in the CE expansion, we have de facto identified the stable region for corrections to arbitrary order: if one of the above effects is enough to maintain stability, any perturbations arising from smaller corrections will be unable to overcome the same effect. However, we have also demonstrated that for plasmas with ![]() $\beta \gg 1$ there exists a significant region of the (
$\beta \gg 1$ there exists a significant region of the (![]() $d_e/L$,
$d_e/L$, ![]() $\lambda /L$) parameter space in which fast, small-scale instabilities are both possible and, in fact, generic. Indeed, in the strongly magnetised plasmas (that is,
$\lambda /L$) parameter space in which fast, small-scale instabilities are both possible and, in fact, generic. Indeed, in the strongly magnetised plasmas (that is, ![]() $\rho _s \ll \lambda _s$ for both electrons and ions) on which we have focused our investigation, it transpires that collisional damping is never able to prevent the most important kinetic instabilities, and thus strongly magnetised, high-
$\rho _s \ll \lambda _s$ for both electrons and ions) on which we have focused our investigation, it transpires that collisional damping is never able to prevent the most important kinetic instabilities, and thus strongly magnetised, high-![]() $\beta$ plasmas cannot be modelled by standard CE theory if
$\beta$ plasmas cannot be modelled by standard CE theory if ![]() $\lambda /L \gtrsim 1/\beta$. This finding has significant implications for our understanding of various plasma environments, including those found in astrophysical contexts and also those created in laser-plasma experiments on high-energy laser facilities.
$\lambda /L \gtrsim 1/\beta$. This finding has significant implications for our understanding of various plasma environments, including those found in astrophysical contexts and also those created in laser-plasma experiments on high-energy laser facilities.
When kinetic instabilities do arise in a CE plasma, we claim that we have characterised the most significant of them systematically. Using an analytical approach based on asymptotic methods, we have been able to derive simple expressions for the thresholds and growth rates of these kinetic instabilities in terms of basic parameters such as ![]() $\beta$,
$\beta$, ![]() $\lambda /L$ and the mass ratio
$\lambda /L$ and the mass ratio ![]() $\mu _e = m_e/m_i$. Three of the instabilities – the CET whistler instability (§ 3.3.1), the CET slow-wave instability (§ 3.3.3), and the CET long-wavelength KAW instability (§ 3.3.4) – are driven by heat fluxes in a CE plasma, while the remaining ten – the CES mirror instability (§ 4.3.1), the CES whistler instability (§ 4.3.2), the CES transverse instability (§§ 4.3.3 and 4.4.9), the CES electron mirror instability (§ 4.3.4), the CES firehose instability (§§ 4.4.2, 4.4.3, 4.4.4, and 4.4.5), the CES parallel and oblique electron firehose instabilities (§§ 4.4.6 and 4.4.7, respectively), the CES EST instability (§ 4.4.8), the CES whisper instability (§ 4.4.10) and the CES ordinary-mode instability (§ 4.4.11) – are driven by ion- and/or electron-velocity shears. While many of these instabilities, or versions thereof, had been considered previously, four of them (the CET slow-wave, CET long-wavelength KAW, CES EST and CES whisper instabilities) are new; the whisper instability in particular seems to be of some interest both conceptually and practically, because it is associated with a newly discovered plasma wave (the whisper wave), and the instability is much faster than its competitors over quite a wide range of values of
$\mu _e = m_e/m_i$. Three of the instabilities – the CET whistler instability (§ 3.3.1), the CET slow-wave instability (§ 3.3.3), and the CET long-wavelength KAW instability (§ 3.3.4) – are driven by heat fluxes in a CE plasma, while the remaining ten – the CES mirror instability (§ 4.3.1), the CES whistler instability (§ 4.3.2), the CES transverse instability (§§ 4.3.3 and 4.4.9), the CES electron mirror instability (§ 4.3.4), the CES firehose instability (§§ 4.4.2, 4.4.3, 4.4.4, and 4.4.5), the CES parallel and oblique electron firehose instabilities (§§ 4.4.6 and 4.4.7, respectively), the CES EST instability (§ 4.4.8), the CES whisper instability (§ 4.4.10) and the CES ordinary-mode instability (§ 4.4.11) – are driven by ion- and/or electron-velocity shears. While many of these instabilities, or versions thereof, had been considered previously, four of them (the CET slow-wave, CET long-wavelength KAW, CES EST and CES whisper instabilities) are new; the whisper instability in particular seems to be of some interest both conceptually and practically, because it is associated with a newly discovered plasma wave (the whisper wave), and the instability is much faster than its competitors over quite a wide range of values of ![]() $\lambda /L$ and
$\lambda /L$ and ![]() $\beta$. The consequences of the existence of the whisper (and EST) instabilities for astrophysical and laser plasmas, in particular for magnetic-field generation, will be addressed in future work.
$\beta$. The consequences of the existence of the whisper (and EST) instabilities for astrophysical and laser plasmas, in particular for magnetic-field generation, will be addressed in future work.
An important question to address is that of the dominant microinstability overall: in a given plasma (with fixed ![]() $d_e/L$,
$d_e/L$, ![]() $\lambda /L$ and
$\lambda /L$ and ![]() $\beta$), amongst the many instabilities that we have found, which is the dominant one? As we explained in § 2.2.3, the answer to this question depends on assumptions about the relative magnitude of temperature- and velocity-gradient scale lengths
$\beta$), amongst the many instabilities that we have found, which is the dominant one? As we explained in § 2.2.3, the answer to this question depends on assumptions about the relative magnitude of temperature- and velocity-gradient scale lengths ![]() $L_T$ and
$L_T$ and ![]() $L_V$. Here, we assume
$L_V$. Here, we assume ![]() ${Ma}\, \lambda /L_V$ to be large enough to trigger all of the aforementioned instabilities, and also adopt the scalings (2.55) in § 2.2.3 for a CE plasma whose largest-scale fluid motions are sonic (
${Ma}\, \lambda /L_V$ to be large enough to trigger all of the aforementioned instabilities, and also adopt the scalings (2.55) in § 2.2.3 for a CE plasma whose largest-scale fluid motions are sonic (![]() ${Ma} \lesssim 1$). As we discussed in the final paragraph of § 2.2.3, our first assumption (which necessitates that
${Ma} \lesssim 1$). As we discussed in the final paragraph of § 2.2.3, our first assumption (which necessitates that ![]() $\beta _i \gg \epsilon _i^{-1}$) in fact supports our second one. We then find that the three most competitive ones are on electron scales: the CET whistler, CES whisper and transverse instabilities. These have growth rates (see (3.10), (4.31) and (4.110), respectively)
$\beta _i \gg \epsilon _i^{-1}$) in fact supports our second one. We then find that the three most competitive ones are on electron scales: the CET whistler, CES whisper and transverse instabilities. These have growth rates (see (3.10), (4.31) and (4.110), respectively)
 $$\begin{align}\gamma_{\mathrm{whisper}} &\sim \frac{|\epsilon_e|^{3/4} \beta_e^{1/4}}{\left[\log{|\epsilon_e| \beta_e}\right]^{1/2}} \varOmega_e \sim \left(\frac{\lambda_{i}}{L_V}\right)^{3/4} \frac{\mu_e^{3/8} {Ma}^{3/4} \beta_e^{1/4}}{\left[\log{\left(\mu_e^{1/2} \beta_e {Ma} \, \lambda_i/L_V \right)}\right]^{1/2}} \varOmega_e , \end{align}$$
$$\begin{align}\gamma_{\mathrm{whisper}} &\sim \frac{|\epsilon_e|^{3/4} \beta_e^{1/4}}{\left[\log{|\epsilon_e| \beta_e}\right]^{1/2}} \varOmega_e \sim \left(\frac{\lambda_{i}}{L_V}\right)^{3/4} \frac{\mu_e^{3/8} {Ma}^{3/4} \beta_e^{1/4}}{\left[\log{\left(\mu_e^{1/2} \beta_e {Ma} \, \lambda_i/L_V \right)}\right]^{1/2}} \varOmega_e , \end{align}$$ $$\begin{align}\gamma_{\mathrm{trans}} &\sim \epsilon_e^{3/2} \beta_e^{1/2} \varOmega_e \sim \mu_e^{3/4} \left(\frac{\lambda_{i}}{L_V}\right)^{3/2} \beta_e^{1/2} \varOmega_e . \end{align}$$
$$\begin{align}\gamma_{\mathrm{trans}} &\sim \epsilon_e^{3/2} \beta_e^{1/2} \varOmega_e \sim \mu_e^{3/4} \left(\frac{\lambda_{i}}{L_V}\right)^{3/2} \beta_e^{1/2} \varOmega_e . \end{align}$$
Although the threshold for the CET whistler instability is less restrictive than for the whisper instability, at the whisper instability threshold ![]() $|\epsilon _e| \beta _e \sim \beta _e^{2/7} \sim |\epsilon _e|^{-2/5}$ it follows that
$|\epsilon _e| \beta _e \sim \beta _e^{2/7} \sim |\epsilon _e|^{-2/5}$ it follows that
 \begin{equation} \frac{\gamma_{{\mathrm{whistler},T}}}{\gamma_{\mathrm{whisper}}} \sim \frac{\eta_e \left[\log{\epsilon_e \beta_e}\right]^{1/2}}{\epsilon_e^{2/5}} \sim \mu_e^{1/20} \left(\frac{\lambda_{i}}{L_V}\right)^{3/5} \left[\log{\left(\mu_e^{1/2} \beta_e {Ma} \, \lambda_i/L_V \right)}\right]^{1/2} \ll 1 . \end{equation}
\begin{equation} \frac{\gamma_{{\mathrm{whistler},T}}}{\gamma_{\mathrm{whisper}}} \sim \frac{\eta_e \left[\log{\epsilon_e \beta_e}\right]^{1/2}}{\epsilon_e^{2/5}} \sim \mu_e^{1/20} \left(\frac{\lambda_{i}}{L_V}\right)^{3/5} \left[\log{\left(\mu_e^{1/2} \beta_e {Ma} \, \lambda_i/L_V \right)}\right]^{1/2} \ll 1 . \end{equation}
Thus, the fact that CE plasmas typically support fluid motions on smaller scales than temperature gradients (see § 2.2.3) implies that CES microinstabilities are more potent at sufficiently high plasma ![]() $\beta _e$. Yet, for
$\beta _e$. Yet, for ![]() $\beta _e \lesssim \mu _e^{-1/2} {Ma}^{-1} \, {L_V}/{\lambda _{i}}$, the CET whistler instability is the most rapidly growing microinstability. Finally, for
$\beta _e \lesssim \mu _e^{-1/2} {Ma}^{-1} \, {L_V}/{\lambda _{i}}$, the CET whistler instability is the most rapidly growing microinstability. Finally, for ![]() $\beta _e \lesssim \mu _e^{-1/4} {Ma}^{-1} L_V/ \lambda _i$, none of these electron-scale instabilities is triggered at all, with only the ion-scale firehose and mirror instabilities operating. In short, the dominant microinstability is a complicated function of the parameter regime. For reference, in table 2 of § 1 we show the (approximate) growth rates for all of the instabilities considered in this paper if the scalings (2.55) are adopted, and figure 1 shows a schematic stability map for the same case.Footnote 9
$\beta _e \lesssim \mu _e^{-1/4} {Ma}^{-1} L_V/ \lambda _i$, none of these electron-scale instabilities is triggered at all, with only the ion-scale firehose and mirror instabilities operating. In short, the dominant microinstability is a complicated function of the parameter regime. For reference, in table 2 of § 1 we show the (approximate) growth rates for all of the instabilities considered in this paper if the scalings (2.55) are adopted, and figure 1 shows a schematic stability map for the same case.Footnote 9
We believe that our study – which is the first systematic investigation of the kinetic stability of a classical, collisional, magnetised plasma – provides a significant step forward towards a comprehensive understanding of this state of matter. It is perhaps inevitable, however, given the conceptual extent of the problem, that there remain a number of questions concerning the stability of the CE distribution function that we have not addressed here. In terms of linear theory, a numerical study using a better collision operator to find the exact stability boundaries could be usefully carried out – although we do not anticipate that this would lead to an alteration of the basic scalings of those boundaries derived in this paper. Another issue not addressed by this work is that of linear coupling between CET and CES microinstabilities; it is not immediately obvious to what extent microinstabilities with similar growth rates might aid each other's growth. The analysis could also be extended to two-species plasmas not in thermal equilibrium, as well as high-![]() $Z_i$ plasmas (with important applications in laser-plasma physics). Numerical simulations using collisional particle-in-cell or Vlasov codes could be employed to confirm the validity of the predictions made in this paper. Another possible research direction that could prove to be fruitful concerns the application of thermodynamic arguments to CE microinstabilities, such as those propounded by Fowler (Reference Fowler1968) and more recently by Helander (Reference Helander2017). Such arguments have previously been used to derive bounds on growth rates, and also the amplitude that unstable electrostatic fluctuations can attain in magnetised plasmas. While the use of analogous arguments to characterise CE microinstabilities would require a generalisation of those arguments to include electromagnetic fluctuations, this may not be too challenging for microinstabilities such as the whisper instability that can be described by reduced models (e.g. gyrokinetics).
$Z_i$ plasmas (with important applications in laser-plasma physics). Numerical simulations using collisional particle-in-cell or Vlasov codes could be employed to confirm the validity of the predictions made in this paper. Another possible research direction that could prove to be fruitful concerns the application of thermodynamic arguments to CE microinstabilities, such as those propounded by Fowler (Reference Fowler1968) and more recently by Helander (Reference Helander2017). Such arguments have previously been used to derive bounds on growth rates, and also the amplitude that unstable electrostatic fluctuations can attain in magnetised plasmas. While the use of analogous arguments to characterise CE microinstabilities would require a generalisation of those arguments to include electromagnetic fluctuations, this may not be too challenging for microinstabilities such as the whisper instability that can be described by reduced models (e.g. gyrokinetics).
Perhaps the most interesting future development of this work would be the determination of transport coefficients for plasmas falling into the unstable regimes. This requires quasi-linear or nonlinear treatment. Nonetheless, the results presented here can be seen as both a guide and a warning to those wishing to address this fundamental question. They are a guide in the sense that a correct characterisation of transport coefficients requires knowledge of the fastest-growing linear modes, which our study provides. But they are also as a warning in that an isolated treatment of one type of microinstability without reference to the full range of possible others could lead to a mischaracterisation of transport properties. The best hope for a correct calculation of transport in a weakly collisional, high-![]() $\beta$ plasma is, therefore, the following programme: for a plasma with particular conditions, identify the fastest microinstability, calculate the saturated magnitude of the fluctuations produced by it, determine the anomalous transport coefficients with those fluctuations present, re-calculate of the stability of this plasma and so on, until a self-consistent picture emerges. It is likely that such a picture will involve a distribution function whose underlying nature depends on macroscopic motions, and hence transport coefficients that are themselves properties of flow shear, temperature gradients and large-scale magnetic fields. Carrying out such calculations is a non-trivial task, but not impossible.
$\beta$ plasma is, therefore, the following programme: for a plasma with particular conditions, identify the fastest microinstability, calculate the saturated magnitude of the fluctuations produced by it, determine the anomalous transport coefficients with those fluctuations present, re-calculate of the stability of this plasma and so on, until a self-consistent picture emerges. It is likely that such a picture will involve a distribution function whose underlying nature depends on macroscopic motions, and hence transport coefficients that are themselves properties of flow shear, temperature gradients and large-scale magnetic fields. Carrying out such calculations is a non-trivial task, but not impossible.
Acknowledgements
A.F.A.B. would like to express his deepest gratitude to M. Kunz and E. Quataert for many helpful discussions about the paper generally, for highlighting some important considerations pertaining to the linear theory of the firehose instability, and for their ongoing support, without which this paper would never have been completed. All the authors would also like to thank A. Spitkovsky for bringing several key early papers on CE microinstabilities to the authors’ attention. In addition, the authors are grateful to the two anonymous reviewers, whose recommendations have improved the paper.
Editor Dmitri Uzdensky thanks the referees for their advice in evaluating this article.
Funding
To carry out this research, A.F.A.B. was supported by DOE awards DE-SC0019046 and DE-SC0019047 through the NSF/DOE Partnership in Basic Plasma Science and Engineering, and also by UKRI (grant number MR/W006723/1). The work of A.A.S. was supported in part by grants from STFC (ST/N000919/1 and ST/W000903/1) and EPSRC (EP/M022331/1 and EP/R034737/1), as well as by the Simons Foundation via a Simons Investigator award. This research was in part funded by Plan S funders (UKRI, STFC and EPSRC).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Glossary of notation used in the paper
As an aid to reading, we provide a glossary of the notation that we use in our paper in tables 5 and 6 of this appendix.
Table 5. Glossary of notation I.

Table 6. Glossary of notation II.

Appendix B. Derivation of the Chapman–Enskog distribution function
B.1. The Chapman–Enskog expansion in strongly magnetised plasma
There exist a number of lucid explanations of how the CE distribution functions (2.8) arise in a collisional, strongly magnetised two-species electron–ion plasma (![]() $\rho _s \ll \lambda _s$ for
$\rho _s \ll \lambda _s$ for ![]() $s = i, e$) – the monograph of Braginskii (Reference Braginskii1965), but also (for example) Helander & Sigmar (Reference Helander and Sigmar2005), Chapter 4. For that reason, we do not provide a full derivation of (2.8). However, in this appendix, we describe a calculation that allows for a direct derivation of the CE distribution function for a strongly magnetised collisional plasma, without first having to perform the CE expansion for arbitrary values of
$s = i, e$) – the monograph of Braginskii (Reference Braginskii1965), but also (for example) Helander & Sigmar (Reference Helander and Sigmar2005), Chapter 4. For that reason, we do not provide a full derivation of (2.8). However, in this appendix, we describe a calculation that allows for a direct derivation of the CE distribution function for a strongly magnetised collisional plasma, without first having to perform the CE expansion for arbitrary values of ![]() $\rho _s/\lambda _s$.
$\rho _s/\lambda _s$.
The first part of the calculation is the same as in Helander & Sigmar (Reference Helander and Sigmar2005, pp. 76–78). For the reader's convenience, we present a summarised version. We consider the Maxwell–Vlasov–Landau equation (2.1) of species ![]() $s$ in a frame co-moving with the fluid rest frame of that species. Defining the peculiar velocity variable
$s$ in a frame co-moving with the fluid rest frame of that species. Defining the peculiar velocity variable ![]() $\boldsymbol {v}_s' = \boldsymbol {v}-\boldsymbol {V}_s$ in the fluid rest frame, (2.1) becomes
$\boldsymbol {v}_s' = \boldsymbol {v}-\boldsymbol {V}_s$ in the fluid rest frame, (2.1) becomes
 \begin{equation} \frac{\mathrm{D} f_{s}}{\mathrm{D} t} + \boldsymbol{v}_s' \boldsymbol{\cdot} \boldsymbol{\nabla} f_{s} + \left[\frac{Z_s e}{m_s} \left(\boldsymbol{E}'+ \frac{\boldsymbol{v}_s' \times \boldsymbol{B}}{c}\right) - \frac{\mathrm{D} \boldsymbol{V}_s}{\mathrm{D} t}\right]\boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} - \boldsymbol{v}_s' \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{V}_s \boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} = \sum_{s'} \mathfrak{C}(f_s,f_{s'}) , \end{equation}
\begin{equation} \frac{\mathrm{D} f_{s}}{\mathrm{D} t} + \boldsymbol{v}_s' \boldsymbol{\cdot} \boldsymbol{\nabla} f_{s} + \left[\frac{Z_s e}{m_s} \left(\boldsymbol{E}'+ \frac{\boldsymbol{v}_s' \times \boldsymbol{B}}{c}\right) - \frac{\mathrm{D} \boldsymbol{V}_s}{\mathrm{D} t}\right]\boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} - \boldsymbol{v}_s' \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{V}_s \boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} = \sum_{s'} \mathfrak{C}(f_s,f_{s'}) , \end{equation}
where ![]() $\boldsymbol {E}' \equiv \boldsymbol {E} + \boldsymbol {V}_s \times \boldsymbol {B}/c$ is the electric field measured in the moving frame, and
$\boldsymbol {E}' \equiv \boldsymbol {E} + \boldsymbol {V}_s \times \boldsymbol {B}/c$ is the electric field measured in the moving frame, and
is the convective derivative. Initially ordering ![]() $\lambda _s \sim \rho _s$, and assuming the plasma is collisional (
$\lambda _s \sim \rho _s$, and assuming the plasma is collisional (![]() $\lambda _{s}/L \ll 1$), we rearrange (B1) so that the largest terms are grouped together (on the left-hand side):
$\lambda _{s}/L \ll 1$), we rearrange (B1) so that the largest terms are grouped together (on the left-hand side):
 \begin{align} &\sum_{s'} \mathfrak{C}(f_s,f_{s'}) - \frac{Z_s e}{m_s c} \left(\boldsymbol{v}_s' \times \boldsymbol{B} \right) \boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} \nonumber\\ &\quad =\frac{\mathrm{D} f_{s}}{\mathrm{D} t} + \boldsymbol{v}_s' \boldsymbol{\cdot} \boldsymbol{\nabla} f_{s} + \left(\frac{Z_s e}{m_s} \boldsymbol{E}' - \frac{\mathrm{D} \boldsymbol{V}_s}{\mathrm{D} t}\right)\boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} - \boldsymbol{v}_s' \boldsymbol{\cdot} \left( \boldsymbol{\nabla} \boldsymbol{V}_s \right)\boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} . \end{align}
\begin{align} &\sum_{s'} \mathfrak{C}(f_s,f_{s'}) - \frac{Z_s e}{m_s c} \left(\boldsymbol{v}_s' \times \boldsymbol{B} \right) \boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} \nonumber\\ &\quad =\frac{\mathrm{D} f_{s}}{\mathrm{D} t} + \boldsymbol{v}_s' \boldsymbol{\cdot} \boldsymbol{\nabla} f_{s} + \left(\frac{Z_s e}{m_s} \boldsymbol{E}' - \frac{\mathrm{D} \boldsymbol{V}_s}{\mathrm{D} t}\right)\boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} - \boldsymbol{v}_s' \boldsymbol{\cdot} \left( \boldsymbol{\nabla} \boldsymbol{V}_s \right)\boldsymbol{\cdot} \frac{\partial f_s}{\partial \boldsymbol{v}_s'} . \end{align}
We then expand the distribution functions ![]() $f_s$ in small parameter
$f_s$ in small parameter ![]() $\lambda _{s}/L \ll 1$:
$\lambda _{s}/L \ll 1$:
and solve (B3) order by order in ![]() $\lambda _{s}/L$ for
$\lambda _{s}/L$ for ![]() $f_{s}^{(0)}$ and
$f_{s}^{(0)}$ and ![]() $f_{s}^{(1)}$. The subsequent treatment of the collision operator for the electron distribution function is a little different from the ion distribution function, so we treat each case individually.
$f_{s}^{(1)}$. The subsequent treatment of the collision operator for the electron distribution function is a little different from the ion distribution function, so we treat each case individually.
B.1.1. Electrons
For the electrons, we can rewrite the total collision operator in a convenient form if we assume that ![]() $T_i \sim T_e$, and
$T_i \sim T_e$, and ![]() $\boldsymbol {V}_i \sim v_{\mathrm {th}i}$:
$\boldsymbol {V}_i \sim v_{\mathrm {th}i}$:
where the electron–electron collision operator ![]() $\mathfrak {C}_{ee}(f_e)$ and electron–ion collision operators
$\mathfrak {C}_{ee}(f_e)$ and electron–ion collision operators ![]() $\mathfrak {C}_{ei}^{(0)}(f_e)$ and
$\mathfrak {C}_{ei}^{(0)}(f_e)$ and ![]() $\mathfrak {C}_{ei}^{(1)}(f_e)$ are
$\mathfrak {C}_{ei}^{(1)}(f_e)$ are
Here, ![]() $\nu _{ei}(v)$ is the velocity-dependent collision frequency
$\nu _{ei}(v)$ is the velocity-dependent collision frequency
and the total electron–ion collision operator ![]() $\mathfrak {C}(f_e,f_i)$ is given by
$\mathfrak {C}(f_e,f_i)$ is given by ![]() $\mathfrak {C}(f_e,f_i) = \mathfrak {C}_{ei}^{(0)}(f_e) + \mathfrak {C}_{ei}^{(1)}(f_e)$. Note that when evaluating
$\mathfrak {C}(f_e,f_i) = \mathfrak {C}_{ei}^{(0)}(f_e) + \mathfrak {C}_{ei}^{(1)}(f_e)$. Note that when evaluating ![]() $\mathfrak {C}_{ei}^{(1)}(f_e)$, we assumed that the deviation of the electron distribution function from a Maxwellian was small. This reformulation of the electron–ion collision operator is possible, because the assumptions
$\mathfrak {C}_{ei}^{(1)}(f_e)$, we assumed that the deviation of the electron distribution function from a Maxwellian was small. This reformulation of the electron–ion collision operator is possible, because the assumptions ![]() $T_i \sim T_e$, and
$T_i \sim T_e$, and ![]() $\boldsymbol {V}_i \sim v_{\mathrm {th}i}$ mean that, from the perspective of the electrons, the ion distribution is sharply peaked around the ion-fluid velocity: in other words,
$\boldsymbol {V}_i \sim v_{\mathrm {th}i}$ mean that, from the perspective of the electrons, the ion distribution is sharply peaked around the ion-fluid velocity: in other words, ![]() $f_i \approx n_{i} \delta (\boldsymbol {v}-\boldsymbol {V}_i)$. Furthermore, the reformulation is convenient because the total electron collision operator (B5) becomes independent of the ion distribution function. Thus, the asymptotic expansion (B4) for the electron distribution function is decoupled from the ions.
$f_i \approx n_{i} \delta (\boldsymbol {v}-\boldsymbol {V}_i)$. Furthermore, the reformulation is convenient because the total electron collision operator (B5) becomes independent of the ion distribution function. Thus, the asymptotic expansion (B4) for the electron distribution function is decoupled from the ions.
Substituting (B5), the ordered kinetic equation (B3) for the electron distribution becomes
 \begin{align} &\mathfrak{C}_{ee}(f_e) + \mathfrak{C}_{ei}^{(0)}(f_e) + \frac{e}{m_e c} \left(\boldsymbol{v}_e' \times \boldsymbol{B} \right)\boldsymbol{\cdot} \frac{\partial f_e}{\partial \boldsymbol{v}_e'} \nonumber\\ & \quad = \frac{\mathrm{D} f_{e}}{\mathrm{D} t} + \boldsymbol{v}_e' \boldsymbol{\cdot} \boldsymbol{\nabla} f_{e} - \left(\frac{e}{m_e} \boldsymbol{E}' + \frac{\mathrm{D} \boldsymbol{V}_e}{\mathrm{D} t}\right)\boldsymbol{\cdot} \frac{\partial f_e}{\partial \boldsymbol{v}_e'} - \boldsymbol{v}_e' \boldsymbol{\cdot} \left( \boldsymbol{\nabla} \boldsymbol{V}_e \right) \boldsymbol{\cdot} \frac{\partial f_e}{\partial \boldsymbol{v}_e'} - \mathfrak{C}_{ei}^{(1)}(f_e) , \end{align}
\begin{align} &\mathfrak{C}_{ee}(f_e) + \mathfrak{C}_{ei}^{(0)}(f_e) + \frac{e}{m_e c} \left(\boldsymbol{v}_e' \times \boldsymbol{B} \right)\boldsymbol{\cdot} \frac{\partial f_e}{\partial \boldsymbol{v}_e'} \nonumber\\ & \quad = \frac{\mathrm{D} f_{e}}{\mathrm{D} t} + \boldsymbol{v}_e' \boldsymbol{\cdot} \boldsymbol{\nabla} f_{e} - \left(\frac{e}{m_e} \boldsymbol{E}' + \frac{\mathrm{D} \boldsymbol{V}_e}{\mathrm{D} t}\right)\boldsymbol{\cdot} \frac{\partial f_e}{\partial \boldsymbol{v}_e'} - \boldsymbol{v}_e' \boldsymbol{\cdot} \left( \boldsymbol{\nabla} \boldsymbol{V}_e \right) \boldsymbol{\cdot} \frac{\partial f_e}{\partial \boldsymbol{v}_e'} - \mathfrak{C}_{ei}^{(1)}(f_e) , \end{align}
where we note that, under assumptions ![]() $T_i \sim T_e$, and
$T_i \sim T_e$, and ![]() $\boldsymbol {V}_i \sim v_{\mathrm {th}i}$,
$\boldsymbol {V}_i \sim v_{\mathrm {th}i}$, ![]() $\mathfrak {C}_{ei}^{(1)}(f_e) \sim \mu _e^{1/2} \mathfrak {C}_{ei}^{(0)}(f_e)$ is much smaller than
$\mathfrak {C}_{ei}^{(1)}(f_e) \sim \mu _e^{1/2} \mathfrak {C}_{ei}^{(0)}(f_e)$ is much smaller than ![]() $\mathfrak {C}_{ei}^{(0)}(f_e)$. Then applying expansion (B4) with
$\mathfrak {C}_{ei}^{(0)}(f_e)$. Then applying expansion (B4) with ![]() $s = e$ gives
$s = e$ gives
 \begin{equation} \mathfrak{C}_{ee}(f_e^{(0)}) + \mathfrak{C}_{ei}^{(0)}(f_e^{(0)}) + \frac{e}{m_e c} \left(\boldsymbol{v}_e' \times \boldsymbol{B} \right) \boldsymbol{\cdot} \frac{\partial f_e^{(0)}}{\partial \boldsymbol{v}_e'} = 0 . \end{equation}
\begin{equation} \mathfrak{C}_{ee}(f_e^{(0)}) + \mathfrak{C}_{ei}^{(0)}(f_e^{(0)}) + \frac{e}{m_e c} \left(\boldsymbol{v}_e' \times \boldsymbol{B} \right) \boldsymbol{\cdot} \frac{\partial f_e^{(0)}}{\partial \boldsymbol{v}_e'} = 0 . \end{equation}It can be shown (Helander & Sigmar Reference Helander and Sigmar2005) that the only solution of (B9) is (as expected) a Maxwellian distribution:
After some algebraic manipulation, it can also be shown that the leading-order perturbed electron distribution function ![]() $f_{e}^{(1)}(\boldsymbol {v})$ satisfies
$f_{e}^{(1)}(\boldsymbol {v})$ satisfies
 \begin{align} &\mathfrak{C}_{ee}(f_{e}^{(1)}) + \mathfrak{C}_{ei}^{(0)}(f_{e}^{(1)}) + \frac{e}{m_e c} \left( \boldsymbol{v}_{e}' \times \boldsymbol{B} \right) \boldsymbol{\cdot} \frac{\partial f_{e}^{(1)}}{\partial \boldsymbol{v}_{e}'}\nonumber\\ &\quad = \left\{\left(\frac{|\boldsymbol{v}_e'|^2}{v_{\mathrm{th}e}^2} -\frac{5}{2}\right)\boldsymbol{v}_{e}' \boldsymbol{\cdot} \boldsymbol{\nabla} \log T_e + \boldsymbol{v}_{e}' \boldsymbol{\cdot} \left[\frac{\boldsymbol{R}_e}{p_e}+ \frac{m_e \boldsymbol{u}_{ei} \nu_{ei}(v)}{T_e} \right] \right. \nonumber\\ & \qquad \left.+ \frac{m_e}{2 T_e} \left(\boldsymbol{v}_{e}' \boldsymbol{v}_{e}' - \frac{|\boldsymbol{v}_e'|^2}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \right\} f_{e}^{(0)} , \end{align}
\begin{align} &\mathfrak{C}_{ee}(f_{e}^{(1)}) + \mathfrak{C}_{ei}^{(0)}(f_{e}^{(1)}) + \frac{e}{m_e c} \left( \boldsymbol{v}_{e}' \times \boldsymbol{B} \right) \boldsymbol{\cdot} \frac{\partial f_{e}^{(1)}}{\partial \boldsymbol{v}_{e}'}\nonumber\\ &\quad = \left\{\left(\frac{|\boldsymbol{v}_e'|^2}{v_{\mathrm{th}e}^2} -\frac{5}{2}\right)\boldsymbol{v}_{e}' \boldsymbol{\cdot} \boldsymbol{\nabla} \log T_e + \boldsymbol{v}_{e}' \boldsymbol{\cdot} \left[\frac{\boldsymbol{R}_e}{p_e}+ \frac{m_e \boldsymbol{u}_{ei} \nu_{ei}(v)}{T_e} \right] \right. \nonumber\\ & \qquad \left.+ \frac{m_e}{2 T_e} \left(\boldsymbol{v}_{e}' \boldsymbol{v}_{e}' - \frac{|\boldsymbol{v}_e'|^2}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \right\} f_{e}^{(0)} , \end{align}
where ![]() $\boldsymbol {R}_e$ and so on are defined in the main text, in (2.12). We note that this manipulation uses the leading-order terms (in
$\boldsymbol {R}_e$ and so on are defined in the main text, in (2.12). We note that this manipulation uses the leading-order terms (in ![]() $\lambda _e/L$) of the moment equations (2.4), and all terms directly involving gradients of density cancel with other terms.
$\lambda _e/L$) of the moment equations (2.4), and all terms directly involving gradients of density cancel with other terms.
B.1.2. Electrons in strongly magnetised limit
We now solve for ![]() $f_{e}^{(1)}$ in a strongly magnetised plasma, i.e.
$f_{e}^{(1)}$ in a strongly magnetised plasma, i.e. ![]() $\rho _e \ll \lambda _e$. In this subsidiary limit, both the collision integrals on the left-hand side of (B11) and the terms on its right-hand side are much smaller than the term proportional to the magnetic field; in other words,
$\rho _e \ll \lambda _e$. In this subsidiary limit, both the collision integrals on the left-hand side of (B11) and the terms on its right-hand side are much smaller than the term proportional to the magnetic field; in other words,
 \begin{equation} \boldsymbol{v}_{e}' \times \boldsymbol{B} \boldsymbol{\cdot} \frac{\partial f_{e}^{(1)}}{\partial \boldsymbol{v}_{e}'} \approx 0 .\end{equation}
\begin{equation} \boldsymbol{v}_{e}' \times \boldsymbol{B} \boldsymbol{\cdot} \frac{\partial f_{e}^{(1)}}{\partial \boldsymbol{v}_{e}'} \approx 0 .\end{equation}
We then define coordinate system ![]() $\{v_{e\|}',v_{e\bot }',\phi '\}$ by
$\{v_{e\|}',v_{e\bot }',\phi '\}$ by ![]() $v_{e\|}' \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \boldsymbol {v}_{e}'$,
$v_{e\|}' \equiv \hat {\boldsymbol {z}} \boldsymbol {\cdot } \boldsymbol {v}_{e}'$, ![]() $\boldsymbol {v}_{e\bot }' = \boldsymbol {v}_{e}' - v_{e\|}' \hat {\boldsymbol {z}}$,
$\boldsymbol {v}_{e\bot }' = \boldsymbol {v}_{e}' - v_{e\|}' \hat {\boldsymbol {z}}$, ![]() ${v}_{e\bot }' = |\boldsymbol {v}_{e\bot }' |$ and
${v}_{e\bot }' = |\boldsymbol {v}_{e\bot }' |$ and ![]() $\phi ' = \phi$, where
$\phi ' = \phi$, where ![]() $\hat {\boldsymbol {z}} = \boldsymbol {B}/|\boldsymbol {B}|$ and
$\hat {\boldsymbol {z}} = \boldsymbol {B}/|\boldsymbol {B}|$ and ![]() $\phi$ is the gyrophase angle. The velocity gradient operator in this system is
$\phi$ is the gyrophase angle. The velocity gradient operator in this system is
 \begin{equation} \frac{\partial f_{e}^{(1)}}{\partial \boldsymbol{v}_e'} = \hat{\boldsymbol{z}}\frac{\partial f_{e}^{(1)}}{\partial v_{e\|}'} + \frac{\boldsymbol{v}_{e\bot}'}{v_{e\bot}'} \frac{\partial f_{e}^{(1)}}{\partial v_{e\bot}'} + \frac{1}{v_{e\bot}'^2} \boldsymbol{v}_e' \times \hat{\boldsymbol{z}} \frac{\partial f_{e}^{(1)}}{\partial \phi'} . \end{equation}
\begin{equation} \frac{\partial f_{e}^{(1)}}{\partial \boldsymbol{v}_e'} = \hat{\boldsymbol{z}}\frac{\partial f_{e}^{(1)}}{\partial v_{e\|}'} + \frac{\boldsymbol{v}_{e\bot}'}{v_{e\bot}'} \frac{\partial f_{e}^{(1)}}{\partial v_{e\bot}'} + \frac{1}{v_{e\bot}'^2} \boldsymbol{v}_e' \times \hat{\boldsymbol{z}} \frac{\partial f_{e}^{(1)}}{\partial \phi'} . \end{equation}
This, when combined with (B12), implies that ![]() $f_{e}^{(1)}$ is approximately gyrotropic:
$f_{e}^{(1)}$ is approximately gyrotropic:
where we have defined the gyro-average ![]() $\langle f_{e}^{(1)}\rangle _{\phi '}$ of the electron distribution function by
$\langle f_{e}^{(1)}\rangle _{\phi '}$ of the electron distribution function by
Now gyro-averaging (B11), we obtain
 \begin{align} &\mathfrak{C}_{ee}\left(\langle f_{e}^{(1)}\rangle_{\phi'}\right) + \mathfrak{C}_{ei}^{(0)}\left(\langle f_{e}^{(1)}\rangle_{\phi'}\right) \nonumber\\ &\quad = \left\{\left[\left(\frac{|\boldsymbol{v}_e'|^2}{v_{\mathrm{th}e}^2} -\frac{5}{2}\right) \boldsymbol{\nabla}_{\|} \log T_e + \frac{R_{e\|}}{p_e} + \frac{m_e u_{ei\|} \nu_{ei}(v)}{T_e} \right] v_{e\|}'\right. \nonumber\\ & \qquad\left. + \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} , \end{align}
\begin{align} &\mathfrak{C}_{ee}\left(\langle f_{e}^{(1)}\rangle_{\phi'}\right) + \mathfrak{C}_{ei}^{(0)}\left(\langle f_{e}^{(1)}\rangle_{\phi'}\right) \nonumber\\ &\quad = \left\{\left[\left(\frac{|\boldsymbol{v}_e'|^2}{v_{\mathrm{th}e}^2} -\frac{5}{2}\right) \boldsymbol{\nabla}_{\|} \log T_e + \frac{R_{e\|}}{p_e} + \frac{m_e u_{ei\|} \nu_{ei}(v)}{T_e} \right] v_{e\|}'\right. \nonumber\\ & \qquad\left. + \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} , \end{align}
where we have used the gyrophase isotropy of the collision operators to commute the order of gyro-averaging on the left-hand side. (B16) is a linear equation for ![]() $\langle f_{e}^{(1)}\rangle _{\phi '}$, so by tensor invariance, it must have a solution of the form
$\langle f_{e}^{(1)}\rangle _{\phi '}$, so by tensor invariance, it must have a solution of the form
 \begin{align} \langle f_{e}^{(1)} \rangle_{\phi'} & = \tau_e \left\{ \left[A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \boldsymbol{\nabla}_{\|} \log T_e +A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \frac{R_{e\|}}{p_e}+ \left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) -1\right)\frac{m_e u_{ei\|}}{T_e \tau_{e}} \right] v_{e\|}'\right. \nonumber\\ & \quad \left.+\, C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} , \end{align}
\begin{align} \langle f_{e}^{(1)} \rangle_{\phi'} & = \tau_e \left\{ \left[A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \boldsymbol{\nabla}_{\|} \log T_e +A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \frac{R_{e\|}}{p_e}+ \left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) -1\right)\frac{m_e u_{ei\|}}{T_e \tau_{e}} \right] v_{e\|}'\right. \nonumber\\ & \quad \left.+\, C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} , \end{align}
where ![]() $\tau _e$ is defined by (2.15a) in the main text, and the isotropic functions
$\tau _e$ is defined by (2.15a) in the main text, and the isotropic functions ![]() $A_e^{T}({|\boldsymbol {v}_e'|}/{v_{\mathrm {th}e}})$,
$A_e^{T}({|\boldsymbol {v}_e'|}/{v_{\mathrm {th}e}})$, ![]() $A_e^{R}({|\boldsymbol {v}_e'|}/{v_{\mathrm {th}e}})$ and
$A_e^{R}({|\boldsymbol {v}_e'|}/{v_{\mathrm {th}e}})$ and ![]() $C\!({|\boldsymbol {v}_e'|}/{v_{\mathrm {th}e}})$ are determined by inverting the collision operators (see Appendix B.2 for an example of how this calculation is done for a simple choice of collision operator). The total electron CE distribution function becomes
$C\!({|\boldsymbol {v}_e'|}/{v_{\mathrm {th}e}})$ are determined by inverting the collision operators (see Appendix B.2 for an example of how this calculation is done for a simple choice of collision operator). The total electron CE distribution function becomes
 \begin{align} f_{e}(v_{e\|}',v_{e\bot}') & = \left\{1 + \tau_e \left[A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \boldsymbol{\nabla}_{\|} \log T_e +A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \frac{R_{e\|}}{p_e}\right.\right. \nonumber\\ & \quad \left.+\,\left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) -1 \right) \frac{m_e u_{ei\|}}{T_e \tau_e} \right] v_{e\|}' \nonumber\\ & \quad \left.+\, C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} . \end{align}
\begin{align} f_{e}(v_{e\|}',v_{e\bot}') & = \left\{1 + \tau_e \left[A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \boldsymbol{\nabla}_{\|} \log T_e +A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \frac{R_{e\|}}{p_e}\right.\right. \nonumber\\ & \quad \left.+\,\left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) -1 \right) \frac{m_e u_{ei\|}}{T_e \tau_e} \right] v_{e\|}' \nonumber\\ & \quad \left.+\, C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} . \end{align}We emphasise that this quantity is expressed in the rest frame of the electron fluid.Footnote 10
Finally, we recover (2.8a) by transforming (B18) into the frame co-moving with the ion fluid. Since ![]() ${u}_{ei\|} \sim \lambda _e v_{\mathrm {th}e}/L \ll v_{\mathrm {th}e}$, this transformation applied to the non-Maxwellian component
${u}_{ei\|} \sim \lambda _e v_{\mathrm {th}e}/L \ll v_{\mathrm {th}e}$, this transformation applied to the non-Maxwellian component ![]() $f_{e}^{(1)}$ of the electron distribution function only produces corrections of magnitude
$f_{e}^{(1)}$ of the electron distribution function only produces corrections of magnitude ![]() $\sim (\lambda _e/L) f_{e}^{(1)}$, and thus any correction terms are negligible. The only important contribution is from the shifted Maxwellian
$\sim (\lambda _e/L) f_{e}^{(1)}$, and thus any correction terms are negligible. The only important contribution is from the shifted Maxwellian
where ![]() $\tilde {\boldsymbol {v}}_e = (\boldsymbol {v}- \boldsymbol {V}_i)/v_{\mathrm {th}e}$. Combining (B19) with (B18), we deduce
$\tilde {\boldsymbol {v}}_e = (\boldsymbol {v}- \boldsymbol {V}_i)/v_{\mathrm {th}e}$. Combining (B19) with (B18), we deduce
 \begin{align} f_{e}(\tilde{v}_{e\|},\tilde{v}_{e\bot}) & = \left\{1 + \left[A_e^{T}\!\left(\tilde{v}_e\right) \lambda_e \boldsymbol{\nabla}_{\|} \log T_e +A_e^{R}\!\left(\tilde{v}_e\right) \lambda_e \frac{R_{e\|}}{p_e} + A_e^{u}\!\left(\tilde{v}_e\right) \lambda_e \frac{m_e u_{ei\|}}{T_e \tau_e} \right] \tilde{v}_{e\|} \right. \nonumber\\ & \quad \left. +\, \tau_e C_e\!\left(\tilde{v}_e\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\tilde{v}_{e\|}^2 - \frac{\tilde{v}_{e\bot}^2}{2} \right) \right\} f_{e}^{(0)} . \end{align}
\begin{align} f_{e}(\tilde{v}_{e\|},\tilde{v}_{e\bot}) & = \left\{1 + \left[A_e^{T}\!\left(\tilde{v}_e\right) \lambda_e \boldsymbol{\nabla}_{\|} \log T_e +A_e^{R}\!\left(\tilde{v}_e\right) \lambda_e \frac{R_{e\|}}{p_e} + A_e^{u}\!\left(\tilde{v}_e\right) \lambda_e \frac{m_e u_{ei\|}}{T_e \tau_e} \right] \tilde{v}_{e\|} \right. \nonumber\\ & \quad \left. +\, \tau_e C_e\!\left(\tilde{v}_e\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\tilde{v}_{e\|}^2 - \frac{\tilde{v}_{e\bot}^2}{2} \right) \right\} f_{e}^{(0)} . \end{align}
Introducing the parameters ![]() $\eta _e^{T}$,
$\eta _e^{T}$, ![]() $\eta _e^{R}$,
$\eta _e^{R}$, ![]() $\eta _e^{u}$ and
$\eta _e^{u}$ and ![]() $\epsilon _e$ defined by (2.11a), (2.11b), (2.11c) and (2.11e) gives the final result (2.8a).
$\epsilon _e$ defined by (2.11a), (2.11b), (2.11c) and (2.11e) gives the final result (2.8a).
B.1.3. Ions
The derivation of the equivalent result (2.8b) for the ion distribution is mostly similar, but with one key difference: the total ion collision operator is dominated by the ion–ion collision operator ![]() $\mathfrak {C}_{ii}(f_i) \equiv \mathfrak {C}(f_i,f_i)$:
$\mathfrak {C}_{ii}(f_i) \equiv \mathfrak {C}(f_i,f_i)$:
This is because ion–electron collisions are small in the mass ratio compared with ion–electron collisions. After some algebra, it can be shown that the equivalent of (B11) for the perturbed ion distribution ![]() $f_i^{(1)}$ is
$f_i^{(1)}$ is
 \begin{align} &\mathfrak{C}_{ii}(f_{i}^{(1)}) - \frac{Z_i e}{m_i c} \left(\boldsymbol{v}_{i}' \times \boldsymbol{B} \right) \boldsymbol{\cdot} \frac{\partial f_{i}^{(1)}}{\partial \boldsymbol{v}_{i}'} \nonumber\\ &\quad =\left[\left(\frac{|\boldsymbol{v}_i'|^2}{v_{\mathrm{th}i}^2} -\frac{5}{2}\right)\boldsymbol{v}_{i}' \boldsymbol{\cdot} \boldsymbol{\nabla} \log T_i + \frac{m_i}{2 T_i} \left(\boldsymbol{v}_{i}' \boldsymbol{v}_{i}' - \frac{|\boldsymbol{v}_i'|^2}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_i \right] f_{i}^{(0)} , \end{align}
\begin{align} &\mathfrak{C}_{ii}(f_{i}^{(1)}) - \frac{Z_i e}{m_i c} \left(\boldsymbol{v}_{i}' \times \boldsymbol{B} \right) \boldsymbol{\cdot} \frac{\partial f_{i}^{(1)}}{\partial \boldsymbol{v}_{i}'} \nonumber\\ &\quad =\left[\left(\frac{|\boldsymbol{v}_i'|^2}{v_{\mathrm{th}i}^2} -\frac{5}{2}\right)\boldsymbol{v}_{i}' \boldsymbol{\cdot} \boldsymbol{\nabla} \log T_i + \frac{m_i}{2 T_i} \left(\boldsymbol{v}_{i}' \boldsymbol{v}_{i}' - \frac{|\boldsymbol{v}_i'|^2}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_i \right] f_{i}^{(0)} , \end{align}where the lowest-order distribution is Maxwellian:
We emphasise that the main differences between (B11) and (B22) are the presence of only one collision operator on the left-hand side of (B22) and the absence of any term proportional to the ion–electron friction force ![]() $\boldsymbol {R}_{ie}$ on the right-hand side of (B22).
$\boldsymbol {R}_{ie}$ on the right-hand side of (B22).
Once (B22) has been written down, the method for obtaining the ion CE distribution function (2.8b) in a strongly magnetised plasma is near-identical to that of the electron distribution function. Gyro-averaging gives
 \begin{equation} \mathfrak{C}_{ii}(f_{i}^{(1)}) = \left[\left(\frac{|\boldsymbol{v}_i'|^2}{v_{\mathrm{th}i}^2} -\frac{5}{2}\right) v_{i\|}' \boldsymbol{\nabla}_{\|} \log T_i + \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_i \left(\frac{v_{i\|}'^2}{v_{\mathrm{th}i}^2} - \frac{v_{i\bot}'^2}{2 v_{\mathrm{th}i}^2} \right) \right] f_{i}^{(0)} , \end{equation}
\begin{equation} \mathfrak{C}_{ii}(f_{i}^{(1)}) = \left[\left(\frac{|\boldsymbol{v}_i'|^2}{v_{\mathrm{th}i}^2} -\frac{5}{2}\right) v_{i\|}' \boldsymbol{\nabla}_{\|} \log T_i + \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_i \left(\frac{v_{i\|}'^2}{v_{\mathrm{th}i}^2} - \frac{v_{i\bot}'^2}{2 v_{\mathrm{th}i}^2} \right) \right] f_{i}^{(0)} , \end{equation}from which it follows that
 \begin{align} f_{i}(v_{i\|}',v_{i\bot}') & = \left[1 + \tau_i A_i\!\left(\frac{|\boldsymbol{v}_i'|}{v_{\mathrm{th}i}}\right) v_{i\|}' \boldsymbol{\nabla}_{\|} \log T_i \right. \nonumber\\ & \quad \left.+\, C_i\!\left(\frac{|\boldsymbol{v}_i'|}{v_{\mathrm{th}i}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_i \left(\frac{v_{i\|}'^2}{v_{\mathrm{th}i}^2} - \frac{v_{i\bot}'^2}{2 v_{\mathrm{th}i}^2} \right) \right] f_{i}^{(0)} . \end{align}
\begin{align} f_{i}(v_{i\|}',v_{i\bot}') & = \left[1 + \tau_i A_i\!\left(\frac{|\boldsymbol{v}_i'|}{v_{\mathrm{th}i}}\right) v_{i\|}' \boldsymbol{\nabla}_{\|} \log T_i \right. \nonumber\\ & \quad \left.+\, C_i\!\left(\frac{|\boldsymbol{v}_i'|}{v_{\mathrm{th}i}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_i \left(\frac{v_{i\|}'^2}{v_{\mathrm{th}i}^2} - \frac{v_{i\bot}'^2}{2 v_{\mathrm{th}i}^2} \right) \right] f_{i}^{(0)} . \end{align}
On substituting for parameters ![]() $\eta _i$ and
$\eta _i$ and ![]() $\epsilon _i$ defined by (2.11d) and (2.11f), respectively, we obtain (2.8b).
$\epsilon _i$ defined by (2.11d) and (2.11f), respectively, we obtain (2.8b).
B.2. Deriving isotropic functions of velocity for the CE solution
In this appendix, we illustrate how to calculate the isotropic functions ![]() $A_e^{T}(\tilde {v}_e)$,
$A_e^{T}(\tilde {v}_e)$, ![]() $A_e^{R}(\tilde {v}_e)$,
$A_e^{R}(\tilde {v}_e)$, ![]() $A_e^{u}(\tilde {v}_e)$,
$A_e^{u}(\tilde {v}_e)$, ![]() $A_i(\tilde {v}_i)$,
$A_i(\tilde {v}_i)$, ![]() $C_e(\tilde {v}_e)$ and
$C_e(\tilde {v}_e)$ and ![]() $C_i(\tilde {v}_i)$ arising in the electron and ion CE distribution functions for the particular cases of two simplified collision operators: the Krook collision operator and the Lorentz collision operator.
$C_i(\tilde {v}_i)$ arising in the electron and ion CE distribution functions for the particular cases of two simplified collision operators: the Krook collision operator and the Lorentz collision operator.
B.2.1. Krook collision operator
The Krook collision operator (Bhatnagar et al. Reference Bhatnagar, Gross and Krook1954) for species ![]() $s$ is given by
$s$ is given by
where ![]() $\tau _s$ is the collision time of species
$\tau _s$ is the collision time of species ![]() $s$ (assumed velocity-independent), and
$s$ (assumed velocity-independent), and
is a Maxwellian distribution with density ![]() $n_s$, mean velocity
$n_s$, mean velocity ![]() $\boldsymbol {V}_e$ and temperature
$\boldsymbol {V}_e$ and temperature ![]() $T_s$ determined from
$T_s$ determined from ![]() $f_s$ via (2.3). For this choice of collision operator, i.e. assuming
$f_s$ via (2.3). For this choice of collision operator, i.e. assuming
for all particle species, calculating the CE distribution function is particularly simple. Substituting (B18) for the electron CE distribution function into the electron Krook collision operator, we find
 \begin{align} \mathfrak{C}_{K}(f_e) & ={-} \left\{ \left[A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \boldsymbol{\nabla}_{\|} \log T_e +A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \frac{R_{e\|}}{p_e}+ \left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) -1\right)\frac{m_e u_{ei\|}}{T_e \tau_{e}} \right] v_{e\|}'\right. \nonumber\\ & \qquad + \left. C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} . \end{align}
\begin{align} \mathfrak{C}_{K}(f_e) & ={-} \left\{ \left[A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \boldsymbol{\nabla}_{\|} \log T_e +A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \frac{R_{e\|}}{p_e}+ \left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) -1\right)\frac{m_e u_{ei\|}}{T_e \tau_{e}} \right] v_{e\|}'\right. \nonumber\\ & \qquad + \left. C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} . \end{align}By comparison with (B16), which, on substituting the Krook operator, becomes
 \begin{align} \mathfrak{C}_{K}(f_e^{(1)}) &= \left\{\left[\left(\frac{|\boldsymbol{v}_e'|^2}{v_{\mathrm{th}e}^2} -\frac{5}{2}\right) \boldsymbol{\nabla}_{\|} \log T_e + \frac{R_{e\|}}{p_e} + \frac{m_e u_{ei\|}}{T_e \tau_{e}} \right] v_{e\|}'\right. \nonumber\\ & \quad \left. +\, \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} , \end{align}
\begin{align} \mathfrak{C}_{K}(f_e^{(1)}) &= \left\{\left[\left(\frac{|\boldsymbol{v}_e'|^2}{v_{\mathrm{th}e}^2} -\frac{5}{2}\right) \boldsymbol{\nabla}_{\|} \log T_e + \frac{R_{e\|}}{p_e} + \frac{m_e u_{ei\|}}{T_e \tau_{e}} \right] v_{e\|}'\right. \nonumber\\ & \quad \left. +\, \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} , \end{align}we can immediately deduce that
The CE electron–ion-drift term vanishes for a Krook operator because the operator neglects inter-species collisions; by the same token, neither ![]() $T_i$ and
$T_i$ and ![]() $T_e$ nor
$T_e$ nor ![]() $\boldsymbol {V}_i$ and
$\boldsymbol {V}_i$ and ![]() $\boldsymbol {V}_e$ will equilibrate.
$\boldsymbol {V}_e$ will equilibrate.
For the ion CE distribution, it follows from (B25) substituted into (B26) that
 \begin{align} \mathfrak{C}_{K}(f_i) ={-} \left[ A_i\!\left(\frac{|\boldsymbol{v}_i'|}{v_{\mathrm{th}i}}\right) v_{i\|}' \boldsymbol{\nabla}_{\|} \log T_i + C_i\!\left(\frac{|\boldsymbol{v}_i'|}{v_{\mathrm{th}i}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_i \left(\frac{v_{i\|}'^2}{v_{\mathrm{th}i}^2} - \frac{v_{i\bot}'^2}{2 v_{\mathrm{th}i}^2} \right) \right] f_{i}^{(0)} , \end{align}
\begin{align} \mathfrak{C}_{K}(f_i) ={-} \left[ A_i\!\left(\frac{|\boldsymbol{v}_i'|}{v_{\mathrm{th}i}}\right) v_{i\|}' \boldsymbol{\nabla}_{\|} \log T_i + C_i\!\left(\frac{|\boldsymbol{v}_i'|}{v_{\mathrm{th}i}}\right) \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_i \left(\frac{v_{i\|}'^2}{v_{\mathrm{th}i}^2} - \frac{v_{i\bot}'^2}{2 v_{\mathrm{th}i}^2} \right) \right] f_{i}^{(0)} , \end{align}which gives, on comparison with (B24), that
B.2.2. Lorentz collision operator
The Lorentz collision operator for species ![]() $s$ is defined by
$s$ is defined by
where ![]() $\nu _s(v)$ is a velocity-dependent scattering rate. We emphasise that the Lorentz collision operator is still simplified and physically complete compared with the full Landau collision operator, as it merely isotropises the distribution function over long times. However, such an operator does arise as the largest component of the electron–ion collision operator (see (B6b)) in Appendix B.1), and is, in fact, the exact electron collision operator in the limit of highly charged ions: the so-called ‘Lorentz approximation’ (Helander & Sigmar Reference Helander and Sigmar2005).
$\nu _s(v)$ is a velocity-dependent scattering rate. We emphasise that the Lorentz collision operator is still simplified and physically complete compared with the full Landau collision operator, as it merely isotropises the distribution function over long times. However, such an operator does arise as the largest component of the electron–ion collision operator (see (B6b)) in Appendix B.1), and is, in fact, the exact electron collision operator in the limit of highly charged ions: the so-called ‘Lorentz approximation’ (Helander & Sigmar Reference Helander and Sigmar2005).
To calculate the electron CE distribution function, we substitute (B18) into the collision operator (B34) (with ![]() $s = e$). Using the identities
$s = e$). Using the identities
for any constant vector ![]() $\boldsymbol {a}$ and any symmetric, traceless, constant matrix
$\boldsymbol {a}$ and any symmetric, traceless, constant matrix ![]() $\boldsymbol{\mathsf{A}}$, it follows that
$\boldsymbol{\mathsf{A}}$, it follows that
 \begin{align} \mathfrak{C}_{L}(f_e) &
={-} \hat{\nu}_{e}(\tilde{v}_e) \left\{ \left[2
A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right)
\boldsymbol{\nabla}_{\|} \log T_e +2
A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right)
\frac{R_{e\|}}{p_e}\right.\right. \nonumber\\ & \quad
\left. +\, 2
\left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right)
-1\right)\frac{m_e u_{ei\|}}{T_e \tau_{e}} \right] v_{e\|}'
\nonumber\\ & \quad \left. +\, 6
C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right)
\left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} -
\frac{1}{3}\boldsymbol{\mathsf{I}} \right) \!
\boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e
\left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} -
\frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\}
f_{e}^{(0)} , \end{align}
\begin{align} \mathfrak{C}_{L}(f_e) &
={-} \hat{\nu}_{e}(\tilde{v}_e) \left\{ \left[2
A_e^{T}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right)
\boldsymbol{\nabla}_{\|} \log T_e +2
A_e^{R}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right)
\frac{R_{e\|}}{p_e}\right.\right. \nonumber\\ & \quad
\left. +\, 2
\left(A_e^{u}\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right)
-1\right)\frac{m_e u_{ei\|}}{T_e \tau_{e}} \right] v_{e\|}'
\nonumber\\ & \quad \left. +\, 6
C_e\!\left(\frac{|\boldsymbol{v}_e'|}{v_{\mathrm{th}e}}\right)
\left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} -
\frac{1}{3}\boldsymbol{\mathsf{I}} \right) \!
\boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e
\left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} -
\frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\}
f_{e}^{(0)} , \end{align}
where ![]() $\hat {\nu }_{s} \equiv \nu _{s}(\tilde {v}_s) \tau _{s}$ is the non-dimensionalised collision rate for species
$\hat {\nu }_{s} \equiv \nu _{s}(\tilde {v}_s) \tau _{s}$ is the non-dimensionalised collision rate for species ![]() $s$. As with the Krook operator, we compare (B36) with (B16), substituting a Lorentz collision operator for the latter, viz.
$s$. As with the Krook operator, we compare (B36) with (B16), substituting a Lorentz collision operator for the latter, viz.
 \begin{align} \mathfrak{C}_{L}(f_e^{(1)}) &= \left\{\left[\left(\frac{|\boldsymbol{v}_e'|^2}{v_{\mathrm{th}e}^2} -\frac{5}{2}\right) \boldsymbol{\nabla}_{\|} \log T_e + \frac{R_{e\|}}{p_e} + \frac{m_e u_{ei\|}\nu_{e}(\tilde{v}_e)}{T_e} \right] v_{e\|}'\right. \nonumber\\ & \quad \left. +\, \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} . \end{align}
\begin{align} \mathfrak{C}_{L}(f_e^{(1)}) &= \left\{\left[\left(\frac{|\boldsymbol{v}_e'|^2}{v_{\mathrm{th}e}^2} -\frac{5}{2}\right) \boldsymbol{\nabla}_{\|} \log T_e + \frac{R_{e\|}}{p_e} + \frac{m_e u_{ei\|}\nu_{e}(\tilde{v}_e)}{T_e} \right] v_{e\|}'\right. \nonumber\\ & \quad \left. +\, \left(\hat{\boldsymbol{z}} \hat{\boldsymbol{z}} - \frac{1}{3}\boldsymbol{\mathsf{I}} \right) \! \boldsymbol{:} \! \boldsymbol{\mathsf{W}}_e \left(\frac{v_{e\|}'^2}{v_{\mathrm{th}e}^2} - \frac{v_{e\bot}'^2}{2 v_{\mathrm{th}e}^2} \right) \right\} f_{e}^{(0)} . \end{align}We deduce from the comparison that
The isotropic functions ![]() $A_i(\tilde {v}_i)$ and
$A_i(\tilde {v}_i)$ and ![]() $C_i(\tilde {v}_i)$, which are given by
$C_i(\tilde {v}_i)$, which are given by
can be deduced in an analogous manner.
Appendix C. Derivation of hot, magnetised plasma dispersion relation for arbitrary distribution functions
In this appendix we re-derive the hot-plasma dispersion relation, given by (2.75) in § 2.4.1 (see also Davidson (Reference Davidson1983), Parra (Reference Parra2017), the latter of whose approaches we follow). Our derivation also introduces a (simplified) collision operator in order to show that substitution (2.124) stated in § 2.5.7 provides a simple technique for including the effect of collisions on linear electromagnetic perturbations.
Consider a kinetic, magnetised plasma in equilibrium composed of one electron species and multiple ions species, with (assumed constant) background magnetic field ![]() $\boldsymbol {B}_0$. As in § 2.4.1, we denote the (gyrotropic) equilibrium distribution function of species
$\boldsymbol {B}_0$. As in § 2.4.1, we denote the (gyrotropic) equilibrium distribution function of species ![]() $s$ as
$s$ as ![]() $f_{s0} = f_{s0}(v_{\|},v_{\bot })$. and then consider a collisionless, linear perturbation
$f_{s0} = f_{s0}(v_{\|},v_{\bot })$. and then consider a collisionless, linear perturbation ![]() $\delta f_s$ to this equilibrium state, with wavevector
$\delta f_s$ to this equilibrium state, with wavevector ![]() $\boldsymbol {k}$ and complex frequency
$\boldsymbol {k}$ and complex frequency ![]() $\omega$:
$\omega$:
The electromagnetic perturbations associated with the perturbed distribution functions have the forms given in (2.69), viz.
and satisfy Faraday's law and the Maxwell–Am![]() $\grave{\rm p}$ere law:
$\grave{\rm p}$ere law:
where the current perturbation is
To close these equations, we relate ![]() $\delta f_s$ to the electromagnetic field perturbations by linearising the Maxwell–Vlasov–Landau equation (2.1). The linearisation
$\delta f_s$ to the electromagnetic field perturbations by linearising the Maxwell–Vlasov–Landau equation (2.1). The linearisation ![]() $f_s= f_{s0} + \delta f_s$ then gives that the perturbed distribution function of species
$f_s= f_{s0} + \delta f_s$ then gives that the perturbed distribution function of species ![]() $s$ satisfies
$s$ satisfies
where we have replaced the full linearised collision operator with a simplified Krook collision operator with constant collision frequency ![]() $\nu _{s} = \tau _s^{-1}$ for species
$\nu _{s} = \tau _s^{-1}$ for species ![]() $s$. For any particular equilibrium distribution function, (C3a), (C3b), (C4) and (C5) are a closed set of governing equations.
$s$. For any particular equilibrium distribution function, (C3a), (C3b), (C4) and (C5) are a closed set of governing equations.
We now write these equations in terms of ![]() $\boldsymbol {k}$ and
$\boldsymbol {k}$ and ![]() $\omega$ using (C1), (E1a) and (C2b):
$\omega$ using (C1), (E1a) and (C2b):
 $$\begin{align}\left(-\mathrm{i} \hat{\omega}_s + \mathrm{i} \boldsymbol{k} \boldsymbol{\cdot} \boldsymbol{v} + \tilde{\varOmega}_s \frac{\partial}{\partial \phi}\right) \widehat{\delta f_s} &={-}\frac{Z_s e}{m_s} \left(\widehat{\delta \boldsymbol{E}} + \frac{\boldsymbol{v} \times \widehat{\delta \boldsymbol{B}}}{c}\right) \boldsymbol{\cdot} \frac{\partial f_{s0}}{\partial \boldsymbol{v}} , \end{align}$$
$$\begin{align}\left(-\mathrm{i} \hat{\omega}_s + \mathrm{i} \boldsymbol{k} \boldsymbol{\cdot} \boldsymbol{v} + \tilde{\varOmega}_s \frac{\partial}{\partial \phi}\right) \widehat{\delta f_s} &={-}\frac{Z_s e}{m_s} \left(\widehat{\delta \boldsymbol{E}} + \frac{\boldsymbol{v} \times \widehat{\delta \boldsymbol{B}}}{c}\right) \boldsymbol{\cdot} \frac{\partial f_{s0}}{\partial \boldsymbol{v}} , \end{align}$$
where we have defined the (signed) Larmor frequency of species ![]() $s$ as
$s$ as
and introduced the modified complex frequency ![]() $\hat {\omega }_s \equiv \omega + \mathrm {i} \nu _s$. Note that
$\hat {\omega }_s \equiv \omega + \mathrm {i} \nu _s$. Note that ![]() $Z_e = -1$, so that
$Z_e = -1$, so that ![]() $\tilde {\varOmega }_e < 0$. We then eliminate
$\tilde {\varOmega }_e < 0$. We then eliminate ![]() $\widehat {\delta \boldsymbol {B}}$ in (C6b) and (C6d) using (C6a) to give
$\widehat {\delta \boldsymbol {B}}$ in (C6b) and (C6d) using (C6a) to give
Next, we derive an expression for ![]() $\widehat {\delta f}_s$ in terms of
$\widehat {\delta f}_s$ in terms of ![]() $\widehat {\delta \boldsymbol {E}}$. For arbitrary wavelengths compared with the Larmor radius
$\widehat {\delta \boldsymbol {E}}$. For arbitrary wavelengths compared with the Larmor radius ![]() $\rho _s$ of species
$\rho _s$ of species ![]() $s$, expressing
$s$, expressing ![]() $\widehat {\delta f}_s$ in terms of the equilibrium distribution function and
$\widehat {\delta f}_s$ in terms of the equilibrium distribution function and ![]() $\widehat {\delta \boldsymbol {E}}$ requires inversion of the gyrophase-angle derivative in (C8). This can be done for any
$\widehat {\delta \boldsymbol {E}}$ requires inversion of the gyrophase-angle derivative in (C8). This can be done for any ![]() $f_{s0}$ in an orthonormal coordinate system with basis vectors
$f_{s0}$ in an orthonormal coordinate system with basis vectors ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ defined by (2.76a–c). By Fourier transforming
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ defined by (2.76a–c). By Fourier transforming ![]() $\widehat {\delta f}_s$ in
$\widehat {\delta f}_s$ in ![]() $\phi$, it can then be shown that
$\phi$, it can then be shown that
 \begin{align} \widehat{\delta f_s} ={-}\frac{Z_s e \mathrm{i}}{m_s \omega} \left(\frac{\partial f_{s0}}{\partial v_{\|}}-\frac{v_{\|}}{v_{\bot}} \frac{\partial f_{s0}}{\partial v_{\bot}}\right) \hat{\boldsymbol{z}} \boldsymbol{\cdot} \widehat{\delta \boldsymbol{E}} + \exp \left(-\mathrm{i} k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot} \sin \phi \right) \sum_{n ={-}\infty}^{\infty} \widehat{\delta f}_{s,n} \exp \left(\mathrm{i} n \phi\right) , \end{align}
\begin{align} \widehat{\delta f_s} ={-}\frac{Z_s e \mathrm{i}}{m_s \omega} \left(\frac{\partial f_{s0}}{\partial v_{\|}}-\frac{v_{\|}}{v_{\bot}} \frac{\partial f_{s0}}{\partial v_{\bot}}\right) \hat{\boldsymbol{z}} \boldsymbol{\cdot} \widehat{\delta \boldsymbol{E}} + \exp \left(-\mathrm{i} k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot} \sin \phi \right) \sum_{n ={-}\infty}^{\infty} \widehat{\delta f}_{s,n} \exp \left(\mathrm{i} n \phi\right) , \end{align}where the series coefficients are given by
and the vector ![]() $\boldsymbol {u}_n$ in the basis
$\boldsymbol {u}_n$ in the basis ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ is
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ is
![]() ${J}_n( k_{\bot } \tilde {\rho }_s \tilde {v}_{s\bot })$ denoting the
${J}_n( k_{\bot } \tilde {\rho }_s \tilde {v}_{s\bot })$ denoting the ![]() $n$th-order Bessel function of the first kind. We can then take advantage of the independence of
$n$th-order Bessel function of the first kind. We can then take advantage of the independence of ![]() $f_{s0}$ of the gyroangle to show that the current perturbation is
$f_{s0}$ of the gyroangle to show that the current perturbation is
 \begin{align} \widehat{\delta \boldsymbol{j}} & ={-} \sum_s \frac{2 {\rm \pi}Z_s^2 e^2 \mathrm{i}}{m_s \omega} \int_{-\infty}^{\infty} \mathrm{d} v_{\|} \int_0^{\infty} \mathrm{d} v_{\bot} \left(v_\bot \frac{\partial f_{s0}}{\partial v_{\|}}-v_{\|} \frac{\partial f_{s0}}{\partial v_{\bot}}\right) v_{\|} \hat{\boldsymbol{z}} \left(\hat{\boldsymbol{z}} \boldsymbol{\cdot} \widehat{\delta \boldsymbol{E}} \right) \nonumber\\ & \quad + \sum_s 2 {\rm \pi}Z_s e \int_{C_L} \mathrm{d} v_{\|} \int_0^{\infty} \mathrm{d} v_{\bot}\, v_\bot^2 \sum_{n ={-}\infty}^{\infty} \widehat{\delta f}_{s,n} \boldsymbol{u}_n , \end{align}
\begin{align} \widehat{\delta \boldsymbol{j}} & ={-} \sum_s \frac{2 {\rm \pi}Z_s^2 e^2 \mathrm{i}}{m_s \omega} \int_{-\infty}^{\infty} \mathrm{d} v_{\|} \int_0^{\infty} \mathrm{d} v_{\bot} \left(v_\bot \frac{\partial f_{s0}}{\partial v_{\|}}-v_{\|} \frac{\partial f_{s0}}{\partial v_{\bot}}\right) v_{\|} \hat{\boldsymbol{z}} \left(\hat{\boldsymbol{z}} \boldsymbol{\cdot} \widehat{\delta \boldsymbol{E}} \right) \nonumber\\ & \quad + \sum_s 2 {\rm \pi}Z_s e \int_{C_L} \mathrm{d} v_{\|} \int_0^{\infty} \mathrm{d} v_{\bot}\, v_\bot^2 \sum_{n ={-}\infty}^{\infty} \widehat{\delta f}_{s,n} \boldsymbol{u}_n , \end{align}
where ![]() $C_L$ denotes the usual Landau contour. This can be written as Ohm's law
$C_L$ denotes the usual Landau contour. This can be written as Ohm's law
where ![]() $\boldsymbol {\sigma }$ is the conductivity tensor. In the absence of collisions (
$\boldsymbol {\sigma }$ is the conductivity tensor. In the absence of collisions (![]() $\nu _s = 0$), this is given by (2.77). If the collision frequency
$\nu _s = 0$), this is given by (2.77). If the collision frequency ![]() $\nu _s \neq 0$ is non-zero, then
$\nu _s \neq 0$ is non-zero, then
from which the substitution (2.124) proposed in § 2.5.7 follows.
Substituting Ohm's law (C13) into Ampère's law (C8a) gives the singular nonlinear eigenvalue equation
where
is the plasma dielectric tensor (2.74). Taking the determinant of (C15) gives the desired result (2.75).
Appendix D. Electrostatic instabilities of CE plasma
In this appendix, we calculate the electrostatic hot-plasma dispersion relation for arbitrary distribution functions (Appendix D.1). We then show (Appendix D.2) that for frequencies ![]() $\omega$ such that
$\omega$ such that ![]() $\tilde {\omega }_{s\|} = \omega /k_{\|} v_{\mathrm {th}s} \ll 1$, the dominant contribution to the longitudinal conductivity
$\tilde {\omega }_{s\|} = \omega /k_{\|} v_{\mathrm {th}s} \ll 1$, the dominant contribution to the longitudinal conductivity ![]() $\hat {\boldsymbol {k}} \boldsymbol {\cdot } \boldsymbol {\sigma } \boldsymbol {\cdot } \hat {\boldsymbol {k}}$ is from the Maxwellian component, and strictly positive; the small
$\hat {\boldsymbol {k}} \boldsymbol {\cdot } \boldsymbol {\sigma } \boldsymbol {\cdot } \hat {\boldsymbol {k}}$ is from the Maxwellian component, and strictly positive; the small ![]() ${O}(\eta _s,\epsilon _s)$ non-Maxwellian distortion associated with the CE distribution function results in only an
${O}(\eta _s,\epsilon _s)$ non-Maxwellian distortion associated with the CE distribution function results in only an ![]() ${O}(\eta _s,\epsilon _s)$ distortion to
${O}(\eta _s,\epsilon _s)$ distortion to ![]() $\hat {\boldsymbol {k}} \boldsymbol {\cdot } \boldsymbol {\sigma } \boldsymbol {\cdot } \hat {\boldsymbol {k}}$. We then illustrate the possibility of electrostatic instabilities associated with the CE distribution function by calculating the growth rate of the parallel CE bump-on-tail instability (Appendix D.3). Finally, in Appendix D.4, we show that the only electrostatic instabilities that can occur have a growth rate which is exponentially small in dimensionless parameters
$\hat {\boldsymbol {k}} \boldsymbol {\cdot } \boldsymbol {\sigma } \boldsymbol {\cdot } \hat {\boldsymbol {k}}$. We then illustrate the possibility of electrostatic instabilities associated with the CE distribution function by calculating the growth rate of the parallel CE bump-on-tail instability (Appendix D.3). Finally, in Appendix D.4, we show that the only electrostatic instabilities that can occur have a growth rate which is exponentially small in dimensionless parameters ![]() ${O}(\eta _s,\epsilon _s)$, for arbitrary frequencies. Thus, it follows that electrostatic instabilities generally have a small growth rate in comparison with electromagnetic instabilities for a CE plasma.
${O}(\eta _s,\epsilon _s)$, for arbitrary frequencies. Thus, it follows that electrostatic instabilities generally have a small growth rate in comparison with electromagnetic instabilities for a CE plasma.
D.1. The electrostatic hot-plasma dispersion relation
Beginning from the singular eigenvalue equation (2.73), viz.
we consider the electrostatic modes, for which ![]() $\widehat {\delta \boldsymbol {E}} = (\hat {\boldsymbol {k}} \boldsymbol {\cdot } \widehat {\delta \boldsymbol {E}}) \hat {\boldsymbol {k}}$. For them, the hot-plasma dispersion relation becomes
$\widehat {\delta \boldsymbol {E}} = (\hat {\boldsymbol {k}} \boldsymbol {\cdot } \widehat {\delta \boldsymbol {E}}) \hat {\boldsymbol {k}}$. For them, the hot-plasma dispersion relation becomes
Employing the expression (2.77) for the conductivity tensor, we calculate the longitudinal conductivity
 \begin{align} \hat{\boldsymbol{k}} \boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} \hat{\boldsymbol{k}} & ={-} \frac{\mathrm{i}}{4 {\rm \pi}\omega} \sum_s \omega_{{\rm p}s}^2 \left[ \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot})\right. \nonumber\\ & \left.\quad +\, \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\hat{\boldsymbol{k}}\boldsymbol{\cdot} \boldsymbol{\mathsf{R}}_{sn} \boldsymbol{\cdot} \hat{\boldsymbol{k}}}{\zeta_{sn} -\tilde{v}_{s\|}} \right] , \end{align}
\begin{align} \hat{\boldsymbol{k}} \boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} \hat{\boldsymbol{k}} & ={-} \frac{\mathrm{i}}{4 {\rm \pi}\omega} \sum_s \omega_{{\rm p}s}^2 \left[ \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot})\right. \nonumber\\ & \left.\quad +\, \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\hat{\boldsymbol{k}}\boldsymbol{\cdot} \boldsymbol{\mathsf{R}}_{sn} \boldsymbol{\cdot} \hat{\boldsymbol{k}}}{\zeta_{sn} -\tilde{v}_{s\|}} \right] , \end{align}where
 \begin{align} \hat{\boldsymbol{k}}\boldsymbol{\cdot} \boldsymbol{\mathsf{R}}_{sn} \boldsymbol{\cdot} \hat{\boldsymbol{k}} & = \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{k^2 \tilde{\rho}_s^2 \tilde{v}_{s\bot}^2} \left(n^2 + 2 n k_{\|} \tilde{\rho}_s \tilde{v}_{s\|} + k_{\|}^2 \tilde{\rho}_s^2 \tilde{v}_{s\|}^2 \right) \nonumber\\ & = \frac{k_{\|}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{k^2 \tilde{v}_{s\bot}^2} \left(\frac{n}{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}\right)^2 . \end{align}
\begin{align} \hat{\boldsymbol{k}}\boldsymbol{\cdot} \boldsymbol{\mathsf{R}}_{sn} \boldsymbol{\cdot} \hat{\boldsymbol{k}} & = \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{k^2 \tilde{\rho}_s^2 \tilde{v}_{s\bot}^2} \left(n^2 + 2 n k_{\|} \tilde{\rho}_s \tilde{v}_{s\|} + k_{\|}^2 \tilde{\rho}_s^2 \tilde{v}_{s\|}^2 \right) \nonumber\\ & = \frac{k_{\|}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{k^2 \tilde{v}_{s\bot}^2} \left(\frac{n}{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}\right)^2 . \end{align}By way of the identity
 \begin{equation} \sum_{n ={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \frac{\left(n/{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}\right)^2}{\zeta_{sn} -\tilde{v}_{s\|}} ={-}\tilde{v}_{s\|} + \tilde{\omega}_{s\|} \sum_{n ={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \frac{n/{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}}{\zeta_{sn} -\tilde{v}_{s\|}} , \end{equation}
\begin{equation} \sum_{n ={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \frac{\left(n/{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}\right)^2}{\zeta_{sn} -\tilde{v}_{s\|}} ={-}\tilde{v}_{s\|} + \tilde{\omega}_{s\|} \sum_{n ={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \frac{n/{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}}{\zeta_{sn} -\tilde{v}_{s\|}} , \end{equation}which follows directly from the Bessel-function identity
 \begin{equation} \sum_{n={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 = 1 , \end{equation}
\begin{equation} \sum_{n={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 = 1 , \end{equation}it follows that
 \begin{align} & \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\hat{\boldsymbol{k}}\boldsymbol{\cdot} \boldsymbol{\mathsf{R}}_{sn} \boldsymbol{\cdot} \hat{\boldsymbol{k}}}{\zeta_{sn}-\tilde{v}_{s\|}} \nonumber\\ &\quad ={-} \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \left[\frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} + \frac{\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot})}{\tilde{\omega}_{s\|}} \right] \nonumber\\ & \qquad + \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \frac{n/{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}}{\zeta_{sn} -\tilde{v}_{s\|}} \nonumber\\ & \qquad + \tilde{\omega}_{s\|}^2 \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \sum_{n ={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \frac{n/{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}}{\zeta_{sn} -\tilde{v}_{s\|}} \nonumber\\ &\quad ={-}\frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \nonumber\\ & \qquad + \frac{2 \tilde{\omega}_{s}^2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left(\tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}} + \frac{n}{k_{\|} \tilde{\rho}_s} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}}\right) \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \, , \end{align}
\begin{align} & \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\hat{\boldsymbol{k}}\boldsymbol{\cdot} \boldsymbol{\mathsf{R}}_{sn} \boldsymbol{\cdot} \hat{\boldsymbol{k}}}{\zeta_{sn}-\tilde{v}_{s\|}} \nonumber\\ &\quad ={-} \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \left[\frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} + \frac{\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot})}{\tilde{\omega}_{s\|}} \right] \nonumber\\ & \qquad + \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \frac{n/{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}}{\zeta_{sn} -\tilde{v}_{s\|}} \nonumber\\ & \qquad + \tilde{\omega}_{s\|}^2 \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \sum_{n ={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \frac{n/{k_{\|} \tilde{\rho}_s} + \tilde{v}_{s\|}}{\zeta_{sn} -\tilde{v}_{s\|}} \nonumber\\ &\quad ={-}\frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}^2}{k^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \nonumber\\ & \qquad + \frac{2 \tilde{\omega}_{s}^2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left(\tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}} + \frac{n}{k_{\|} \tilde{\rho}_s} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}}\right) \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \, , \end{align}
where ![]() $\tilde {\omega }_{s} \equiv \omega /k v_{\mathrm {th}s}$. We conclude that
$\tilde {\omega }_{s} \equiv \omega /k v_{\mathrm {th}s}$. We conclude that
 \begin{align} \hat{\boldsymbol{k}} \boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} \hat{\boldsymbol{k}} ={-} \frac{\mathrm{i}}{4 {\rm \pi}\omega} \sum_s \omega_{{\rm p}s}^2 \left[ \tilde{\omega}_{s}^2 \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \right] , \end{align}
\begin{align} \hat{\boldsymbol{k}} \boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} \hat{\boldsymbol{k}} ={-} \frac{\mathrm{i}}{4 {\rm \pi}\omega} \sum_s \omega_{{\rm p}s}^2 \left[ \tilde{\omega}_{s}^2 \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \right] , \end{align}where
 \begin{equation} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \equiv \tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}} + \frac{n}{k_{\|} \tilde{\rho}_s} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} . \end{equation}
\begin{equation} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \equiv \tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}} + \frac{n}{k_{\|} \tilde{\rho}_s} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} . \end{equation}The electrostatic component of the dielectric tensor is then
 \begin{equation} \mathfrak{E}_{33} = k^2 + \sum_s k_{{\rm D}s}^2 \left[ \frac{1}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \right] , \end{equation}
\begin{equation} \mathfrak{E}_{33} = k^2 + \sum_s k_{{\rm D}s}^2 \left[ \frac{1}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \right] , \end{equation}and the electrostatic hot-plasma dispersion relation (D2) becomes
 \begin{equation} k^2 + \sum_s k_{{\rm D}s}^2 \left[ \frac{1}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \right] = 0 , \end{equation}
\begin{equation} k^2 + \sum_s k_{{\rm D}s}^2 \left[ \frac{1}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \right] = 0 , \end{equation}
where the Debye wavenumber ![]() $k_{{\rm D}s}$ of species
$k_{{\rm D}s}$ of species ![]() $s$ is defined by
$s$ is defined by
D.2. The electrostatic dielectric response at low frequencies
In this appendix, we perform a Taylor expansion of the electrostatic component ![]() $\mathfrak {E}_{33}$ of the dielectric tensor (D10) in
$\mathfrak {E}_{33}$ of the dielectric tensor (D10) in ![]() $\tilde {\omega }_{s\|} \ll 1$. Before carrying out the expansion, we first substitute the identity
$\tilde {\omega }_{s\|} \ll 1$. Before carrying out the expansion, we first substitute the identity
into (D10), which then becomes
 \begin{align} \mathfrak{E}_{33} & = k^2 - \sum_s k_{{\rm D}s}^2 \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \nonumber\\ &\quad + \sum_s k_{{\rm D}s}^2 \left[ \frac{\tilde{\omega}_{s\|}}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \right] . \end{align}
\begin{align} \mathfrak{E}_{33} & = k^2 - \sum_s k_{{\rm D}s}^2 \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \nonumber\\ &\quad + \sum_s k_{{\rm D}s}^2 \left[ \frac{\tilde{\omega}_{s\|}}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\zeta_{sn} -\tilde{v}_{s\|}} \right] . \end{align}
Now carrying out the Taylor expansion in ![]() $\tilde {\omega }_{s\|} \ll 1$, we see that, to the leading order in this expansion,
$\tilde {\omega }_{s\|} \ll 1$, we see that, to the leading order in this expansion,
For the CE distribution
we have
where the term in the CE distribution function proportional to ![]() $\eta _s$ has vanished on account of having odd parity with respect to
$\eta _s$ has vanished on account of having odd parity with respect to ![]() $\tilde {v}_{s\|}$. We conclude that the non-Maxwellian contribution to (D17) is
$\tilde {v}_{s\|}$. We conclude that the non-Maxwellian contribution to (D17) is ![]() ${O}(\eta _s,\epsilon _s)$ in comparison with the Maxwellian contribution, and so the electrostatic component of the dielectric tensor for low-frequency fluctuations is just
${O}(\eta _s,\epsilon _s)$ in comparison with the Maxwellian contribution, and so the electrostatic component of the dielectric tensor for low-frequency fluctuations is just
or, writing (D18) explicitly in terms of ![]() $\tilde {\omega }_{s\|}$ and the plasma frequency
$\tilde {\omega }_{s\|}$ and the plasma frequency ![]() $\omega _{{\rm p}s}$ of species
$\omega _{{\rm p}s}$ of species ![]() $s$,
$s$,
 \begin{equation} \mathfrak{E}_{33} \approx k^2 + \sum_s \frac{\omega_{{\rm p}s}^2}{\omega^2} \frac{2 k_{\|}^2}{k^2} \tilde{\omega}_{s\|}^2 . \end{equation}
\begin{equation} \mathfrak{E}_{33} \approx k^2 + \sum_s \frac{\omega_{{\rm p}s}^2}{\omega^2} \frac{2 k_{\|}^2}{k^2} \tilde{\omega}_{s\|}^2 . \end{equation}
It follows that ![]() $\mathfrak {E}_{33}^{(0)}$ and
$\mathfrak {E}_{33}^{(0)}$ and ![]() $\mathfrak {E}_{33}^{(1)}$ defined by (2.99) are given by
$\mathfrak {E}_{33}^{(1)}$ defined by (2.99) are given by
 $$\begin{align}\mathfrak{E}_{33}^{(1)} &= \frac{\omega_{{\rm p}e}^2}{\omega^2} \sum_s \frac{Z_s T_e}{T_s} \frac{2 k_{\|}^2}{k^2} . \end{align}$$
$$\begin{align}\mathfrak{E}_{33}^{(1)} &= \frac{\omega_{{\rm p}e}^2}{\omega^2} \sum_s \frac{Z_s T_e}{T_s} \frac{2 k_{\|}^2}{k^2} . \end{align}$$
where we have neglected the displacement current term (![]() $k \ll k_{{\rm D}e}$), and the temperature of species
$k \ll k_{{\rm D}e}$), and the temperature of species ![]() $s$ is denoted by
$s$ is denoted by ![]() $T_s$.
$T_s$.
D.3. Existence of electrostatic instabilities for a CE plasma
That electrostatic instabilities can exist is most simply shown in the limit of purely parallel, high-frequency fluctuations: ![]() $k_{\bot } = 0$,
$k_{\bot } = 0$, ![]() $k_{\|} = k$,
$k_{\|} = k$, ![]() $\tilde {\omega }_{s} = \tilde {\omega }_{s\|}\gg 1$ and
$\tilde {\omega }_{s} = \tilde {\omega }_{s\|}\gg 1$ and
For purely parallel modes, the only non-zero term in the sum of Bessel functions in the electrostatic hot-plasma dispersion relation (D11) is the ![]() $n = 0$ term; thus, (D11) simplifies to
$n = 0$ term; thus, (D11) simplifies to
 \begin{equation} \mathfrak{E}_{33} = k^2 + \sum_s k_{{\rm D}s}^2 \left( \frac{1}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}} \frac{1}{\tilde{\omega}_{s} -\tilde{v}_{s\|}} \right) = 0 . \end{equation}
\begin{equation} \mathfrak{E}_{33} = k^2 + \sum_s k_{{\rm D}s}^2 \left( \frac{1}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}} \frac{1}{\tilde{\omega}_{s} -\tilde{v}_{s\|}} \right) = 0 . \end{equation}
Next, we expand (D22) around the real frequency ![]() $\varpi$, using (D21); this gives
$\varpi$, using (D21); this gives
Taking the imaginary part of (D23) allows for an expression for ![]() $\gamma$ to be derived in terms of
$\gamma$ to be derived in terms of ![]() $\varpi$:
$\varpi$:
To calculate ![]() $\gamma$, we use
$\gamma$, we use
 $$\begin{align} {\rm Re}{\,\mathfrak{E}_{33}(\varpi, k)} &= k^2 + \sum_s k_{{\rm D}s}^2 \left( \frac{1}{\sqrt{\rm \pi}} {P} \! \int \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}} \frac{1}{\tilde{\omega}_{s} -\tilde{v}_{s\|}} \right) , \end{align}$$
$$\begin{align} {\rm Re}{\,\mathfrak{E}_{33}(\varpi, k)} &= k^2 + \sum_s k_{{\rm D}s}^2 \left( \frac{1}{\sqrt{\rm \pi}} {P} \! \int \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}} \frac{1}{\tilde{\omega}_{s} -\tilde{v}_{s\|}} \right) , \end{align}$$ $$\begin{align}{\rm Im}{\,\mathfrak{E}_{33}(\varpi, k)} &={-}\sqrt{\rm \pi} k^{2} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}}\!\left(\tilde{\omega}_{s},\tilde{v}_{s\bot}\right) , \end{align}$$
$$\begin{align}{\rm Im}{\,\mathfrak{E}_{33}(\varpi, k)} &={-}\sqrt{\rm \pi} k^{2} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}}\!\left(\tilde{\omega}_{s},\tilde{v}_{s\bot}\right) , \end{align}$$
where, to the leading order, ![]() $\tilde {\omega }_{s} \approx \varpi /k v_{\mathrm {th}s}$. Now expanding (D25a) in
$\tilde {\omega }_{s} \approx \varpi /k v_{\mathrm {th}s}$. Now expanding (D25a) in ![]() $\tilde {\omega }_{s} \gg 1$, we find that
$\tilde {\omega }_{s} \gg 1$, we find that
 \begin{equation} {\rm Re}{\,\mathfrak{E}_{33}(\varpi, k)} \approx k^2 - \sum_s \frac{k_{{\rm D}s}^2}{\tilde{\omega}_{s}^2} \approx k^2 \left(1-\frac{\omega_{{\rm p}e}^2}{\varpi^2}\right) , \end{equation}
\begin{equation} {\rm Re}{\,\mathfrak{E}_{33}(\varpi, k)} \approx k^2 - \sum_s \frac{k_{{\rm D}s}^2}{\tilde{\omega}_{s}^2} \approx k^2 \left(1-\frac{\omega_{{\rm p}e}^2}{\varpi^2}\right) , \end{equation}where we have integrated (D25a) by parts, used identity
and neglected the small ion contribution to the dielectric tensor. We conclude that – as expected – the real frequency of such modes is simply the plasma frequency: ![]() $\varpi \approx \pm \omega _{{\rm p}e}$. This in turn implies that
$\varpi \approx \pm \omega _{{\rm p}e}$. This in turn implies that
In other words, electrostatic modes in this limit are simply plasma oscillations with wavelengths much greater than the Debye length.
We immediately deduce that if ![]() $\varpi \approx \omega _{{\rm p}e}$ (without loss of generality, we can consider the mode with
$\varpi \approx \omega _{{\rm p}e}$ (without loss of generality, we can consider the mode with ![]() $\varpi > 0$), then
$\varpi > 0$), then
which in turn implies that ![]() $\gamma$ is positive if and only if, for some
$\gamma$ is positive if and only if, for some ![]() $k$,
$k$,
For the electron CE distribution function (2.72), we have
 \begin{align} \frac{\partial \tilde{f}_{e0}}{\partial \tilde{v}_{e\|}} & ={-} \exp \left(-\tilde{v}_{e}^2\right) \left\{2 \tilde{v}_{e\|} + \eta_e \left[\left(2 \tilde{v}_{e\|}^2 - 1\right) A_e(\tilde{v}_e) - \frac{\tilde{v}_{e\|}^2}{\tilde{v}_e} A_e'(\tilde{v}_e) \right]\right. \nonumber\\ & \quad \left.+\, \epsilon_e \left[ 2 \tilde{v}_{e\|} C_e(\tilde{v}_e) \left(\tilde{v}_{e\|}^2-\frac{\tilde{v}_{e\bot}^2}{2}-1\right) - \frac{\tilde{v}_{e\|}}{\tilde{v}_e} \left(\tilde{v}_{e\|}^2-\frac{\tilde{v}_{e\bot}^2}{2}\right) C_e'(\tilde{v}_e) \right] \vphantom{\left[\left(2 \tilde{v}_{e\|}^2 - 1\right) A_e(\tilde{v}_e) - \frac{\tilde{v}_{e\|}^2}{\tilde{v}_e} A_e'(\tilde{v}_e) \right]}\right\} . \end{align}
\begin{align} \frac{\partial \tilde{f}_{e0}}{\partial \tilde{v}_{e\|}} & ={-} \exp \left(-\tilde{v}_{e}^2\right) \left\{2 \tilde{v}_{e\|} + \eta_e \left[\left(2 \tilde{v}_{e\|}^2 - 1\right) A_e(\tilde{v}_e) - \frac{\tilde{v}_{e\|}^2}{\tilde{v}_e} A_e'(\tilde{v}_e) \right]\right. \nonumber\\ & \quad \left.+\, \epsilon_e \left[ 2 \tilde{v}_{e\|} C_e(\tilde{v}_e) \left(\tilde{v}_{e\|}^2-\frac{\tilde{v}_{e\bot}^2}{2}-1\right) - \frac{\tilde{v}_{e\|}}{\tilde{v}_e} \left(\tilde{v}_{e\|}^2-\frac{\tilde{v}_{e\bot}^2}{2}\right) C_e'(\tilde{v}_e) \right] \vphantom{\left[\left(2 \tilde{v}_{e\|}^2 - 1\right) A_e(\tilde{v}_e) - \frac{\tilde{v}_{e\|}^2}{\tilde{v}_e} A_e'(\tilde{v}_e) \right]}\right\} . \end{align}
As shown in Appendix B.2.1, for a Krook collision operator it follows that (assuming ![]() $\eta _e^R = \eta _e^u = 0$)
$\eta _e^R = \eta _e^u = 0$)
We then see that
 \begin{align} {\rm Im}{\,\mathfrak{E}_{33}(\omega_{{\rm p}e}, k)} & = \sqrt{\rm \pi} k^2 \left[ \frac{k_{{{\rm D}}e}}{\sqrt{2} k} - \eta_e \left(\frac{k_{{\rm D}e}^2}{4 k^2} -\frac{3}{4} \right) \left(\frac{k_{{\rm D}e}^2}{k^2} - 1\right)\right. \nonumber\\ & \quad \left. -\, \epsilon_e \frac{k_{{\rm D}e}}{\sqrt{2} k} \left(\frac{k_{{\rm D}e}^2}{2 k^2}-\frac{3}{2}\right)\right] \exp \left(-\frac{k_{{\rm D}e}^2}{2 k^2}\right) . \end{align}
\begin{align} {\rm Im}{\,\mathfrak{E}_{33}(\omega_{{\rm p}e}, k)} & = \sqrt{\rm \pi} k^2 \left[ \frac{k_{{{\rm D}}e}}{\sqrt{2} k} - \eta_e \left(\frac{k_{{\rm D}e}^2}{4 k^2} -\frac{3}{4} \right) \left(\frac{k_{{\rm D}e}^2}{k^2} - 1\right)\right. \nonumber\\ & \quad \left. -\, \epsilon_e \frac{k_{{\rm D}e}}{\sqrt{2} k} \left(\frac{k_{{\rm D}e}^2}{2 k^2}-\frac{3}{2}\right)\right] \exp \left(-\frac{k_{{\rm D}e}^2}{2 k^2}\right) . \end{align}
This expression changes sign from negative to positive when ![]() $k \lesssim \eta _e^{1/3} k_{{\rm D}e}$, or
$k \lesssim \eta _e^{1/3} k_{{\rm D}e}$, or ![]() $k \lesssim \epsilon _e^{1/2} k_{{\rm D}e}$; thus, plasma waves with sufficiently long wavelengths are driven unstable by the non-Maxwellian component of the CE distribution function. Physically, this is the bump-on-tail instability; this arises because the distribution function is no longer monotonically decreasing at (parallel) particle velocities
$k \lesssim \epsilon _e^{1/2} k_{{\rm D}e}$; thus, plasma waves with sufficiently long wavelengths are driven unstable by the non-Maxwellian component of the CE distribution function. Physically, this is the bump-on-tail instability; this arises because the distribution function is no longer monotonically decreasing at (parallel) particle velocities ![]() $v_{\|} \gtrsim \eta _e^{-1/3} v_{\mathrm {th}e}$, or
$v_{\|} \gtrsim \eta _e^{-1/3} v_{\mathrm {th}e}$, or ![]() $v_{\|} \gtrsim \eta _e^{-1/3} v_{\mathrm {th}e}$, and so plasma waves can extract energy from particles via the Landau resonance.
$v_{\|} \gtrsim \eta _e^{-1/3} v_{\mathrm {th}e}$, and so plasma waves can extract energy from particles via the Landau resonance.
Substituting (D33) into (D24), the growth rate of instabilities satisfying ![]() $k \ll k_{{\rm D}e}$ becomes
$k \ll k_{{\rm D}e}$ becomes
Maximising this expression with respect to ![]() $k$, it can then be shown that the peak growth rate for CE electron-temperature-gradient-driven microinstabilities (
$k$, it can then be shown that the peak growth rate for CE electron-temperature-gradient-driven microinstabilities (![]() $\epsilon _e = 0$) is
$\epsilon _e = 0$) is
at the wavenumber
 \begin{equation} k_{\mathrm{peak}} \approx \frac{\eta_e^{1/3}}{\sqrt{2}} \left[1-\frac{\eta_e^{2/3}}{2} \right] k_{{\rm D}e} , \end{equation}
\begin{equation} k_{\mathrm{peak}} \approx \frac{\eta_e^{1/3}}{\sqrt{2}} \left[1-\frac{\eta_e^{2/3}}{2} \right] k_{{\rm D}e} , \end{equation}
whereas for CE electron-shear-driven microinstabilities (![]() $\eta _e = 0$)
$\eta _e = 0$)
at the wavenumber
 \begin{equation} k_{\mathrm{peak}} \approx \frac{\epsilon_e^{1/2}}{\sqrt{2}} \left[1-\frac{\epsilon_e}{2} \right] k_{{\rm D}e} . \end{equation}
\begin{equation} k_{\mathrm{peak}} \approx \frac{\epsilon_e^{1/2}}{\sqrt{2}} \left[1-\frac{\epsilon_e}{2} \right] k_{{\rm D}e} . \end{equation}D.4. Impossibility of electrostatic instabilities with ‘fast’ growth rates
The existence of electrostatic instabilities was demonstrated in Appendix (D.3); however, the growth rates of the exemplified instabilities were shown to be exponentially small in the parameters ![]() $\eta _e$ or
$\eta _e$ or ![]() $\epsilon _e$. In this appendix, we provide a proof that there cannot exist electrostatic instabilities whose growth rate scales algebraically with
$\epsilon _e$. In this appendix, we provide a proof that there cannot exist electrostatic instabilities whose growth rate scales algebraically with ![]() $\eta _s$ or
$\eta _s$ or ![]() $\epsilon _s$.
$\epsilon _s$.
To substantiate this claim properly, it is necessary to consider perturbations with frequencies ![]() $\omega$ satisfying
$\omega$ satisfying ![]() $\omega \ll k_{\|} v_{\mathrm {th}s}$ and
$\omega \ll k_{\|} v_{\mathrm {th}s}$ and ![]() $\omega \gtrsim k_{\|} v_{\mathrm {th}s}$ separately.
$\omega \gtrsim k_{\|} v_{\mathrm {th}s}$ separately.
D.4.1. Low-frequency electrostatic modes:  $\omega \ll k_{\|} v_{\mathrm {th}s}$
$\omega \ll k_{\|} v_{\mathrm {th}s}$
The impossibility of low-frequency electrostatic instabilities follows immediately from (D18), which shows that the leading-order term in the ![]() $\tilde {\omega }_{s\|} \ll 1$ expansion of the electrostatic component of the dielectric tensor is non-zero. It follows that the electrostatic component of the dielectric tensor is strictly positive at low frequencies. Since the electrostatic component of the dielectric tensor must vanish in order for the electrostatic dispersion relation (D11) to be satisfied, we conclude that there do not exist electrostatic modes with
$\tilde {\omega }_{s\|} \ll 1$ expansion of the electrostatic component of the dielectric tensor is non-zero. It follows that the electrostatic component of the dielectric tensor is strictly positive at low frequencies. Since the electrostatic component of the dielectric tensor must vanish in order for the electrostatic dispersion relation (D11) to be satisfied, we conclude that there do not exist electrostatic modes with ![]() $\omega \ll k_{\|} v_{\mathrm {th}s}$, let alone instabilities.
$\omega \ll k_{\|} v_{\mathrm {th}s}$, let alone instabilities.
D.4.2. Other electrostatic modes:  $\omega \gtrsim k_{\|} v_{\mathrm {th}s}$
$\omega \gtrsim k_{\|} v_{\mathrm {th}s}$
For all other electrostatic perturbations, we suppose that there exist microinstabilities with growth rates which scale algebraically with ![]() $\eta _s$,
$\eta _s$, ![]() $\epsilon _s$, and then prove that that such a supposition is incompatible with the hot-plasma electrostatic dispersion relation.
$\epsilon _s$, and then prove that that such a supposition is incompatible with the hot-plasma electrostatic dispersion relation.
Consider some unstable perturbation satisfying the electrostatic dispersion relation (D11), with complex frequency ![]() $\omega = \varpi + \mathrm {i} \gamma$, and
$\omega = \varpi + \mathrm {i} \gamma$, and ![]() $\gamma > 0$. We then define
$\gamma > 0$. We then define
so that ![]() $\tilde {\omega }_{s\|} = \tilde {\varpi }_{s\|} + \mathrm {i} \tilde {\gamma }_{s\|}$. For unstable perturbations satisfying (D11), it follows from the real and imaginary parts of the dispersion relation that
$\tilde {\omega }_{s\|} = \tilde {\varpi }_{s\|} + \mathrm {i} \tilde {\gamma }_{s\|}$. For unstable perturbations satisfying (D11), it follows from the real and imaginary parts of the dispersion relation that
 \begin{align} 0 & = k^2 - \sum_s k_{{\rm D}s}^2 \left\{ \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left[\vphantom{\frac{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right){J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot})\right.\right. \nonumber\\ & \quad \left.\left.\times\, \frac{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right){J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \right] \right\} , \end{align}
\begin{align} 0 & = k^2 - \sum_s k_{{\rm D}s}^2 \left\{ \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left[\vphantom{\frac{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right){J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot})\right.\right. \nonumber\\ & \quad \left.\left.\times\, \frac{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right){J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \right] \right\} , \end{align} \begin{align} 0 & = \gamma \sum_s k_{{\rm D}s}^2 \mu_s^{{-}1/2} \left\{ \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left[\vphantom{\frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} } \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot})\right.\right. \nonumber\\ & \quad \left.\left.\times\, \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \right] \right\} , \end{align}
\begin{align} 0 & = \gamma \sum_s k_{{\rm D}s}^2 \mu_s^{{-}1/2} \left\{ \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left[\vphantom{\frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} } \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot})\right.\right. \nonumber\\ & \quad \left.\left.\times\, \frac{{J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \right] \right\} , \end{align}
where ![]() $\mu _s \equiv m_e/m_s$, and we have utilised the fact that the Landau contour simplifies to the real line for unstable perturbations. Using (D40b), we can eliminate part of (D40a) to give
$\mu _s \equiv m_e/m_s$, and we have utilised the fact that the Landau contour simplifies to the real line for unstable perturbations. Using (D40b), we can eliminate part of (D40a) to give
 \begin{align} 0 & = k^2 - \sum_s k_{{\rm D}s}^2 \left\{ \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left[ \vphantom{\frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right){J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot})\right.\right. \nonumber\\ & \quad \left.\left.\times\, \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right){J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \right] \right\} . \end{align}
\begin{align} 0 & = k^2 - \sum_s k_{{\rm D}s}^2 \left\{ \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left[ \vphantom{\frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right){J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot})\right.\right. \nonumber\\ & \quad \left.\left.\times\, \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right){J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \right] \right\} . \end{align}
Next, we substitute for ![]() $\varPi _n(\tilde {v}_{s\|},\tilde {v}_{s\bot })$ using
$\varPi _n(\tilde {v}_{s\|},\tilde {v}_{s\bot })$ using
 \begin{equation} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) = \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) + \left(\tilde{v}_{s\|}+\frac{n}{k_{\|} \tilde{\rho}_s}\right) \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} , \end{equation}
\begin{equation} \varPi_n(\tilde{v}_{s\|},\tilde{v}_{s\bot}) = \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) + \left(\tilde{v}_{s\|}+\frac{n}{k_{\|} \tilde{\rho}_s}\right) \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} , \end{equation}to give
 \begin{align} 0 & = k^2 - \sum_s k_{{\rm D}s}^2 \left\{ \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left[\frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}\right.\right. \nonumber\\ & \quad \left.\left.+\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}\right] \right\} . \end{align}
\begin{align} 0 & = k^2 - \sum_s k_{{\rm D}s}^2 \left\{ \frac{1}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \sum_{n ={-}\infty}^{\infty} \left[\frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}\right.\right. \nonumber\\ & \quad \left.\left.+\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}\right] \right\} . \end{align}This expression is very helpful for contradicting the premise of the existence of unstable electrostatic modes. We illustrate this claim with a simple example – a pure Maxwellian distribution function – before considering the CE distribution.
For a Maxwellian distribution for which ![]() $\varLambda _s(\tilde {v}_{s\|},\tilde {v}_{s\bot }) = 0$, and
$\varLambda _s(\tilde {v}_{s\|},\tilde {v}_{s\bot }) = 0$, and
(D43) becomes
 \begin{align} 0 & = k^2 + \sum_s k_{{\rm D}s}^2 \left[ \vphantom{\sum_{n ={-}\infty}^{\infty} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}} \frac{2}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \right. \nonumber\\ & \quad \left.\times\, \sum_{n ={-}\infty}^{\infty} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \right] . \end{align}
\begin{align} 0 & = k^2 + \sum_s k_{{\rm D}s}^2 \left[ \vphantom{\sum_{n ={-}\infty}^{\infty} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2}} \frac{2}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \right. \nonumber\\ & \quad \left.\times\, \sum_{n ={-}\infty}^{\infty} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \right] . \end{align}The integrand on the right-hand side of (D45) is strictly positive – a contradiction. Therefore, we recover the standard result that there cannot exist unstable perturbations if the underlying distribution is Maxwellian.
We now consider the CE distribution (2.72). In order for an instability to arise, it is clear that the integrand on the right-hand side of (D43) has to be positive – and further, the contribution of the integrand from that interval has to dominate all other (negative) contributions to the total integral. To prove that these conditions cannot be satisfied for the CE distribution function, we consider the two terms in the integrand on the right-hand side of (D43) separately.
For the first term
 \begin{equation} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} > 0\end{equation}
\begin{equation} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} > 0\end{equation}if and only if
For the CE distribution function (2.72),
 \begin{align} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} & ={-} \tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \left\{2 + \eta_s \left[2 \tilde{v}_{s\|} A_s(\tilde{v}_s) - \frac{\tilde{v}_{s\|}}{\tilde{v}_s} A_s'(\tilde{v}_s) \right]\right. \nonumber\\ & \left.\quad +\, \epsilon_s \left[ 2 C_s(\tilde{v}_s) \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}+\frac{1}{2}\right) - \frac{1}{\tilde{v}_s} \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}\right) C_s'(\tilde{v}_s) \right] \right\} . \end{align}
\begin{align} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} & ={-} \tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \left\{2 + \eta_s \left[2 \tilde{v}_{s\|} A_s(\tilde{v}_s) - \frac{\tilde{v}_{s\|}}{\tilde{v}_s} A_s'(\tilde{v}_s) \right]\right. \nonumber\\ & \left.\quad +\, \epsilon_s \left[ 2 C_s(\tilde{v}_s) \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}+\frac{1}{2}\right) - \frac{1}{\tilde{v}_s} \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}\right) C_s'(\tilde{v}_s) \right] \right\} . \end{align}
Thus, for ![]() $\tilde {v}_{s\bot } \lesssim 1$ and
$\tilde {v}_{s\bot } \lesssim 1$ and ![]() $\tilde {v}_{s\|} \lesssim 1$, we see that
$\tilde {v}_{s\|} \lesssim 1$, we see that ![]() ${\partial \tilde {f}_{s0}}/{\partial \tilde {v}_{s\bot }} < 0$, because
${\partial \tilde {f}_{s0}}/{\partial \tilde {v}_{s\bot }} < 0$, because ![]() $\eta _s, \epsilon _s \ll 1$. The only values of
$\eta _s, \epsilon _s \ll 1$. The only values of ![]() $\tilde {v}_{s}$ where this inequality could be reversed are large:
$\tilde {v}_{s}$ where this inequality could be reversed are large: ![]() $\tilde {v}_{s} \gg 1$. Assuming that
$\tilde {v}_{s} \gg 1$. Assuming that ![]() $A_s(\tilde {v}_{s}) \sim \tilde {v}_{s}^{\iota _\eta }$ and
$A_s(\tilde {v}_{s}) \sim \tilde {v}_{s}^{\iota _\eta }$ and ![]() $C_s(\tilde {v}_{s}) \sim \tilde {v}_{s}^{\iota _\epsilon }$ for
$C_s(\tilde {v}_{s}) \sim \tilde {v}_{s}^{\iota _\epsilon }$ for ![]() $\tilde {v}_{s} \gg 1$, where
$\tilde {v}_{s} \gg 1$, where ![]() ${\iota _\eta }$ and
${\iota _\eta }$ and ![]() ${\iota _\epsilon }$ are constants, it follows that, for
${\iota _\epsilon }$ are constants, it follows that, for
the non-Maxwellian terms are comparable to the Maxwellian ones. However, for such ![]() $\tilde {v}_{s}$
$\tilde {v}_{s}$
while
 \begin{equation} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \lesssim \frac{\tilde{\varpi}_{s\|}^2}{\tilde{\gamma}_{s\|}^2}, \end{equation}
\begin{equation} \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \lesssim \frac{\tilde{\varpi}_{s\|}^2}{\tilde{\gamma}_{s\|}^2}, \end{equation}
if it is assumed that ![]() $|\varpi | \gg |\gamma |$. Since we assumed that
$|\varpi | \gg |\gamma |$. Since we assumed that ![]() $\tilde {\gamma }_{s\|}$ is only algebraically small in
$\tilde {\gamma }_{s\|}$ is only algebraically small in ![]() $\epsilon _s$ and/or
$\epsilon _s$ and/or ![]() $\eta _s$, we conclude that the contribution to the integrand on the right-hand side of (D43) from
$\eta _s$, we conclude that the contribution to the integrand on the right-hand side of (D43) from ![]() $\tilde {v}_{s}$ satisfying (D49a,b) is asymptotically small compared with other contributions, and thus cannot change the sign of the total integral.
$\tilde {v}_{s}$ satisfying (D49a,b) is asymptotically small compared with other contributions, and thus cannot change the sign of the total integral.
For the second term, we consider the ![]() $n$th term of the sum independently. Recalling from (2.92) that
$n$th term of the sum independently. Recalling from (2.92) that
it follows that for ![]() $\tilde {v}_{s} \sim 1$
$\tilde {v}_{s} \sim 1$
Thus, for ![]() $\tilde {v}_{s} \sim 1$, the non-Maxwellian term is only comparable to the Maxwellian one for
$\tilde {v}_{s} \sim 1$, the non-Maxwellian term is only comparable to the Maxwellian one for ![]() $|\tilde {v}_{s\|} + n/k_{\|} \tilde {\rho }_s| \lesssim \eta _s, \epsilon _s$. However, this non-Maxwellian contribution is in fact always smaller than other non-Maxwellian contributions, which by (D53) are in turn smaller than the equivalent Maxwellian contributions.
$|\tilde {v}_{s\|} + n/k_{\|} \tilde {\rho }_s| \lesssim \eta _s, \epsilon _s$. However, this non-Maxwellian contribution is in fact always smaller than other non-Maxwellian contributions, which by (D53) are in turn smaller than the equivalent Maxwellian contributions.
Depending on the magnitude of ![]() $|n/k_{\|} \tilde {\rho }_s|$, this claim is justified in two different ways.
$|n/k_{\|} \tilde {\rho }_s|$, this claim is justified in two different ways.
(i)
 $\underline{|n/k_{\|} \tilde {\rho }_s| \lesssim 1}$: in this case, let the interval of non-dimensionalised parallel velocities
$\underline{|n/k_{\|} \tilde {\rho }_s| \lesssim 1}$: in this case, let the interval of non-dimensionalised parallel velocities  $\tilde {v}_{s\|}$ satisfying
$\tilde {v}_{s\|}$ satisfying  $|\tilde {v}_{s\|} + n/k_{\|} \tilde {\rho }_s| \lesssim \eta _s, \epsilon _s$ be denoted by
$|\tilde {v}_{s\|} + n/k_{\|} \tilde {\rho }_s| \lesssim \eta _s, \epsilon _s$ be denoted by  $\mathcal {I}$. Then, there exists another finite interval of
$\mathcal {I}$. Then, there exists another finite interval of  $\tilde {v}_{s\|} \sim 1$ such that
$\tilde {v}_{s\|} \sim 1$ such that  $|\tilde {v}_{s\|} + n/k_{\|} \tilde {\rho }_s| \sim 1$. It therefore follows that
(D54)where we have assumed that
$|\tilde {v}_{s\|} + n/k_{\|} \tilde {\rho }_s| \sim 1$. It therefore follows that
(D54)where we have assumed that \begin{align} &\int_{\mathcal{I}} \mathrm{d} \tilde{v}_{s\|} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \nonumber\\ &\quad \sim \eta_s^2 \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|}\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} , \end{align}
\begin{align} &\int_{\mathcal{I}} \mathrm{d} \tilde{v}_{s\|} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} \nonumber\\ &\quad \sim \eta_s^2 \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|}\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \frac{\left(\tilde{v}_{s\|} + n/k_{\|} \tilde{\rho}_s\right) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{\left(\tilde{v}_{s\|} - \tilde{\varpi}_{s\|} + n/k_{\|} \tilde{\rho}_s\right)^2 + \tilde{\gamma}_{s\|}^2} , \end{align} $|\tilde {\varpi }_{s\|}| \gg |\tilde {\gamma }_{s\|}|$ (and also
$|\tilde {\varpi }_{s\|}| \gg |\tilde {\gamma }_{s\|}|$ (and also  $|\tilde {\varpi }_{s\|}| \gtrsim 1$). The claim immediately follows.
$|\tilde {\varpi }_{s\|}| \gtrsim 1$). The claim immediately follows.(ii)
 $\underline{|n/k_{\|} \tilde {\rho }_s| \gg 1}$: in this case, it follows immediately that
$\underline{|n/k_{\|} \tilde {\rho }_s| \gg 1}$: in this case, it follows immediately that  $|\tilde {v}_{s\|} + n/k_{\|} \tilde {\rho }_s| \lesssim \eta _s, \epsilon _s$ if and only if
$|\tilde {v}_{s\|} + n/k_{\|} \tilde {\rho }_s| \lesssim \eta _s, \epsilon _s$ if and only if  $\tilde {v}_{s\|} \gg 1$. Via a similar argument to that presented for large
$\tilde {v}_{s\|} \gg 1$. Via a similar argument to that presented for large  $\tilde {v}_{s\|}$ for the first term in the integrand on the right-hand side of (D43), contributions to the total integral will be exponentially small in
$\tilde {v}_{s\|}$ for the first term in the integrand on the right-hand side of (D43), contributions to the total integral will be exponentially small in  $\eta _s, \epsilon _s$, and thus are unable to reverse the sign of the total integral.
$\eta _s, \epsilon _s$, and thus are unable to reverse the sign of the total integral.
Thus, we have confirmed that there cannot exist electrostatic instabilities with growth rates which are algebraic in small parameters ![]() $\eta _s, \epsilon _s$.
$\eta _s, \epsilon _s$.
Appendix E. Weak growth of high-frequency perturbations
In this appendix, we present an argument that all perturbations in a CE plasma with complex frequency ![]() $\omega = \varpi +\mathrm {i}\gamma$ satisfying the ‘high-frequency’ conditions
$\omega = \varpi +\mathrm {i}\gamma$ satisfying the ‘high-frequency’ conditions ![]() $|\omega | \gtrsim k_{\|} v_{\mathrm {th}s}$ and
$|\omega | \gtrsim k_{\|} v_{\mathrm {th}s}$ and ![]() $|\varpi | \gg |\gamma |$ for all particle species have a growth rate that is at most exponentially small in
$|\varpi | \gg |\gamma |$ for all particle species have a growth rate that is at most exponentially small in ![]() $\eta _s$, and
$\eta _s$, and ![]() $\epsilon _s$. This argument does not prove that all perturbations satisfying
$\epsilon _s$. This argument does not prove that all perturbations satisfying ![]() $|\omega | \gtrsim k_{\|} v_{\mathrm {th}s}$ in a CE plasma are stable, in that it does not apply to perturbations whose damping or growth rate is not small compared with their frequency.
$|\omega | \gtrsim k_{\|} v_{\mathrm {th}s}$ in a CE plasma are stable, in that it does not apply to perturbations whose damping or growth rate is not small compared with their frequency.
E.1. Deriving conditions for stability
We begin with the result that for any linear electromagnetic perturbation with real frequency ![]() $\varpi > 0$, growth rate
$\varpi > 0$, growth rate ![]() $\gamma$, wavevector
$\gamma$, wavevector ![]() $\boldsymbol {k}$ and electric-field perturbation
$\boldsymbol {k}$ and electric-field perturbation
the dissipation rate ![]() $\mathfrak {Q}$ of the perturbation is related to the anti-Hermitian part of the plasma dielectric tensor evaluated at the perturbation's real frequency (Pitaevskii & Lifshitz Reference Pitaevskii and Lifshitz1981):
$\mathfrak {Q}$ of the perturbation is related to the anti-Hermitian part of the plasma dielectric tensor evaluated at the perturbation's real frequency (Pitaevskii & Lifshitz Reference Pitaevskii and Lifshitz1981):
where the anti-Hermitian part ![]() $\boldsymbol {\mathfrak {E}}^{A}$ is defined by
$\boldsymbol {\mathfrak {E}}^{A}$ is defined by
with ![]() $\boldsymbol {\mathfrak {E}}^{{\dagger} }$ representing the conjugate transpose of
$\boldsymbol {\mathfrak {E}}^{{\dagger} }$ representing the conjugate transpose of ![]() $\boldsymbol {\mathfrak {E}}$. If the mode is damped, then the dissipation rate is positive:
$\boldsymbol {\mathfrak {E}}$. If the mode is damped, then the dissipation rate is positive: ![]() $\mathfrak {Q} > 0$. Since
$\mathfrak {Q} > 0$. Since ![]() $\boldsymbol {\mathfrak {E}}^{A}$ is anti-Hermitian, it is diagonalisable in some orthonormal basis
$\boldsymbol {\mathfrak {E}}^{A}$ is anti-Hermitian, it is diagonalisable in some orthonormal basis ![]() $\{\hat {\boldsymbol {e}}_a,\hat {\boldsymbol {e}}_b,\hat {\boldsymbol {e}}_c\}$, with imaginary eigenvalues
$\{\hat {\boldsymbol {e}}_a,\hat {\boldsymbol {e}}_b,\hat {\boldsymbol {e}}_c\}$, with imaginary eigenvalues ![]() $(-\mathrm {i}\varsigma _{a},-\mathrm {i}\varsigma _{b},-\mathrm {i}\varsigma _{c})$, where
$(-\mathrm {i}\varsigma _{a},-\mathrm {i}\varsigma _{b},-\mathrm {i}\varsigma _{c})$, where ![]() $\varsigma _{a}$,
$\varsigma _{a}$, ![]() $\varsigma _{b}$ and
$\varsigma _{b}$ and ![]() $\varsigma _{c}$ are real numbers. The dissipation rate
$\varsigma _{c}$ are real numbers. The dissipation rate ![]() $\mathfrak {Q}$ can be written in terms of these eigenvectors as
$\mathfrak {Q}$ can be written in terms of these eigenvectors as
Thus, for unstable perturbations to exist, it must be the case that at least one of the numbers ![]() $\varsigma _{a}$,
$\varsigma _{a}$, ![]() $\varsigma _{b}$ and
$\varsigma _{b}$ and ![]() $\varsigma _{c}$ has to be negative (without loss of generality, we will assume
$\varsigma _{c}$ has to be negative (without loss of generality, we will assume ![]() $\varsigma _{a} < 0$); if this is the case, then the dissipation rate (and hence the growth rate) is a linear function of
$\varsigma _{a} < 0$); if this is the case, then the dissipation rate (and hence the growth rate) is a linear function of ![]() $\varsigma _{a}$. We will show that if
$\varsigma _{a}$. We will show that if ![]() $|\omega | \gtrsim k_{\|} v_{\mathrm {th}s}$,
$|\omega | \gtrsim k_{\|} v_{\mathrm {th}s}$, ![]() $\varsigma _{a}$,
$\varsigma _{a}$, ![]() $\varsigma _{b}$ and
$\varsigma _{b}$ and ![]() $\varsigma _{c}$ can only be negative if they are exponentially small in
$\varsigma _{c}$ can only be negative if they are exponentially small in ![]() $\eta _s$ and
$\eta _s$ and ![]() $\epsilon _s$.
$\epsilon _s$.
To prove this, consider the characteristic polynomial
of ![]() $\boldsymbol {\mathfrak {E}}^{A}$ evaluated at the real frequency
$\boldsymbol {\mathfrak {E}}^{A}$ evaluated at the real frequency ![]() $\varpi$ and wavevector
$\varpi$ and wavevector ![]() $\boldsymbol {k}$; it is a cubic, and thus can be written
$\boldsymbol {k}$; it is a cubic, and thus can be written
where ![]() $\varrho _0$,
$\varrho _0$, ![]() $\varrho _1$ and
$\varrho _1$ and ![]() $\varrho _2$ depend on
$\varrho _2$ depend on ![]() $\boldsymbol {\mathfrak {E}}^{A}$. Since
$\boldsymbol {\mathfrak {E}}^{A}$. Since ![]() $\boldsymbol {\mathfrak {E}}^{A}$ has eigenvalues
$\boldsymbol {\mathfrak {E}}^{A}$ has eigenvalues ![]() $(-\mathrm {i}\varsigma _{a},-\mathrm {i}\varsigma _{b},-\mathrm {i}\varsigma _{c})$, it follows that
$(-\mathrm {i}\varsigma _{a},-\mathrm {i}\varsigma _{b},-\mathrm {i}\varsigma _{c})$, it follows that
 \begin{align} \varrho(\varsigma) & ={-}\left(\varsigma+\mathrm{i}\varsigma_{a}\right) \left(\varsigma+\mathrm{i}\varsigma_{b}\right) \left(\varsigma+\mathrm{i}\varsigma_{c}\right) \nonumber\\ & ={-}\varsigma^3 - \mathrm{i} \varsigma^2 \left(\varsigma_{a}+\varsigma_{b}+\varsigma_{c}\right) + \varsigma \left(\varsigma_{a}\varsigma_{b}+\varsigma_{b}\varsigma_{c}+\varsigma_{c}\varsigma_{a}\right) + \mathrm{i} \varsigma_{a}\varsigma_{b} \varsigma_{c} , \end{align}
\begin{align} \varrho(\varsigma) & ={-}\left(\varsigma+\mathrm{i}\varsigma_{a}\right) \left(\varsigma+\mathrm{i}\varsigma_{b}\right) \left(\varsigma+\mathrm{i}\varsigma_{c}\right) \nonumber\\ & ={-}\varsigma^3 - \mathrm{i} \varsigma^2 \left(\varsigma_{a}+\varsigma_{b}+\varsigma_{c}\right) + \varsigma \left(\varsigma_{a}\varsigma_{b}+\varsigma_{b}\varsigma_{c}+\varsigma_{c}\varsigma_{a}\right) + \mathrm{i} \varsigma_{a}\varsigma_{b} \varsigma_{c} , \end{align}and so
This implies that ![]() $\varsigma _{a}$,
$\varsigma _{a}$, ![]() $\varsigma _{b}$ and
$\varsigma _{b}$ and ![]() $\varsigma _{c}$ are positive if
$\varsigma _{c}$ are positive if ![]() $\varrho _0$,
$\varrho _0$, ![]() $\varrho _1$ and
$\varrho _1$ and ![]() $\varrho _2$ are positive. Furthermore,
$\varrho _2$ are positive. Furthermore, ![]() $\varrho _0$,
$\varrho _0$, ![]() $\varrho _1$ and
$\varrho _1$ and ![]() $\varrho _2$ can be used to provide bounds for
$\varrho _2$ can be used to provide bounds for ![]() $\varsigma _{a}$,
$\varsigma _{a}$, ![]() $\varsigma _{b}$ and
$\varsigma _{b}$ and ![]() $\varsigma _{c}$ using an inequality discovered by Laguerre (Reference Laguerre1880):
$\varsigma _{c}$ using an inequality discovered by Laguerre (Reference Laguerre1880):
where
In particular, the expression (E10) for the root bounds implies that if ![]() $\varrho _1$ and
$\varrho _1$ and ![]() $\varrho _2$ are exponentially small in
$\varrho _2$ are exponentially small in ![]() $\eta _s$ and
$\eta _s$ and ![]() $\epsilon _s$, then so are
$\epsilon _s$, then so are ![]() $\varsigma _{a}$,
$\varsigma _{a}$, ![]() $\varsigma _{b}$ and
$\varsigma _{b}$ and ![]() $\varsigma _{c}$.
$\varsigma _{c}$.
We can also evaluate ![]() $\varrho (\varsigma )$ in terms of the components of
$\varrho (\varsigma )$ in terms of the components of ![]() $\boldsymbol {\mathfrak {E}}^{A}$ in the coordinate basis
$\boldsymbol {\mathfrak {E}}^{A}$ in the coordinate basis ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$:
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$:
 \begin{align} \varrho(\varsigma) & ={-}\varsigma^3 + \varsigma^2 \left(\mathfrak{E}_{xx}^{A}+\mathfrak{E}_{yy}^{A}+\mathfrak{E}_{zz}^{A}\right) \nonumber\\ &\quad - \varsigma \left(\mathfrak{E}_{xx}^{A} \mathfrak{E}_{yy}^{A} + \mathfrak{E}_{yy}^{A} \mathfrak{E}_{zz}^{A}+ \mathfrak{E}_{zz}^{A} \mathfrak{E}_{xx}^{A} + (\mathfrak{E}_{xy}^{A})^2 + (\mathfrak{E}_{yz}^{A})^2 + (\mathfrak{E}_{xz}^{A})^2\right) + \mbox{det}\,\boldsymbol{\mathfrak{E}}^{A} , \qquad \quad \end{align}
\begin{align} \varrho(\varsigma) & ={-}\varsigma^3 + \varsigma^2 \left(\mathfrak{E}_{xx}^{A}+\mathfrak{E}_{yy}^{A}+\mathfrak{E}_{zz}^{A}\right) \nonumber\\ &\quad - \varsigma \left(\mathfrak{E}_{xx}^{A} \mathfrak{E}_{yy}^{A} + \mathfrak{E}_{yy}^{A} \mathfrak{E}_{zz}^{A}+ \mathfrak{E}_{zz}^{A} \mathfrak{E}_{xx}^{A} + (\mathfrak{E}_{xy}^{A})^2 + (\mathfrak{E}_{yz}^{A})^2 + (\mathfrak{E}_{xz}^{A})^2\right) + \mbox{det}\,\boldsymbol{\mathfrak{E}}^{A} , \qquad \quad \end{align}
where we have used the symmetries (2.87a–c) of the dielectric tensor to give ![]() $\varrho (\varsigma )$ in terms of only the (six) independent components of
$\varrho (\varsigma )$ in terms of only the (six) independent components of ![]() $\boldsymbol {\mathfrak {E}}^{A}$. (E11) gives
$\boldsymbol {\mathfrak {E}}^{A}$. (E11) gives
The anti-Hermiticity of ![]() $\boldsymbol {\mathfrak {E}}^{A}$ implies that
$\boldsymbol {\mathfrak {E}}^{A}$ implies that ![]() ${\rm Im}{\,\mathfrak {E}_{xx}^{A}} = - \mathrm {i} \mathfrak {E}_{xx}^{A}$,
${\rm Im}{\,\mathfrak {E}_{xx}^{A}} = - \mathrm {i} \mathfrak {E}_{xx}^{A}$, ![]() ${\rm Im}{\,\mathfrak {E}_{yy}^{A}} = - \mathrm {i} \mathfrak {E}_{yy}^{A}$,
${\rm Im}{\,\mathfrak {E}_{yy}^{A}} = - \mathrm {i} \mathfrak {E}_{yy}^{A}$, ![]() ${\rm Im}{\,\mathfrak {E}_{zz}^{A}} = - \mathrm {i} \mathfrak {E}_{zz}^{A}$ and
${\rm Im}{\,\mathfrak {E}_{zz}^{A}} = - \mathrm {i} \mathfrak {E}_{zz}^{A}$ and ![]() ${\rm Im}{\,\mathfrak {E}_{xz}^{A}} = - \mathrm {i} \mathfrak {E}_{xz}^{A}$, while
${\rm Im}{\,\mathfrak {E}_{xz}^{A}} = - \mathrm {i} \mathfrak {E}_{xz}^{A}$, while ![]() ${\rm Re}{\,\mathfrak {E}_{xy}^{A}} = \mathfrak {E}_{xy}^{A}$ and
${\rm Re}{\,\mathfrak {E}_{xy}^{A}} = \mathfrak {E}_{xy}^{A}$ and ![]() ${\rm Re}{\,\mathfrak {E}_{yz}^{A}} = \mathfrak {E}_{yz}^{A}$, as is indeed necessary for
${\rm Re}{\,\mathfrak {E}_{yz}^{A}} = \mathfrak {E}_{yz}^{A}$, as is indeed necessary for ![]() $\varrho _0$,
$\varrho _0$, ![]() $\varrho _1$, and
$\varrho _1$, and ![]() $\varrho _2$ to be real numbers. Thus, in order to establish stability it is sufficient for our purposes to show that
$\varrho _2$ to be real numbers. Thus, in order to establish stability it is sufficient for our purposes to show that
When these inequalities are not strictly satisfied, then we can instead estimate the magnitude of (E12b) and (E12c) to determine bounds for ![]() $\varsigma _{a}$,
$\varsigma _{a}$, ![]() $\varsigma _{b}$ and
$\varsigma _{b}$ and ![]() $\varsigma _{c}$.
$\varsigma _{c}$.
E.2. Evaluating conditions for stability
Combining (2.74) with (2.77) gives an expression for the general plasma dielectric tensor (assuming ![]() $k_{\|} > 0$ without loss of generality):
$k_{\|} > 0$ without loss of generality):
 \begin{align} \boldsymbol{\mathfrak{E}} & = \boldsymbol{\mathsf{I}} + \sum_s \frac{\omega_{{\rm p}s}^2}{\omega^2} \left[ \vphantom{\sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{v}_{s\|}}} \frac{2}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \hat{\boldsymbol{z}} \hat{\boldsymbol{z}}\right. \nonumber\\ &\quad \left.+\, \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{v}_{s\|}} \right] , \end{align}
\begin{align} \boldsymbol{\mathfrak{E}} & = \boldsymbol{\mathsf{I}} + \sum_s \frac{\omega_{{\rm p}s}^2}{\omega^2} \left[ \vphantom{\sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{v}_{s\|}}} \frac{2}{\sqrt{\rm \pi}} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \hat{\boldsymbol{z}} \hat{\boldsymbol{z}}\right. \nonumber\\ &\quad \left.+\, \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{v}_{s\|}} \right] , \end{align}
where all salient quantities are defined in § 2.4.1. Now evaluating the anti-Hermitian part of (E14) for ![]() $\omega = \varpi$,
$\omega = \varpi$, ![]() $\tilde {\omega }_{s\|} = \tilde {\varpi }_{s\|}$, we find
$\tilde {\omega }_{s\|} = \tilde {\varpi }_{s\|}$, we find
 \begin{equation} \boldsymbol{\mathfrak{E}}^A ={-}\mathrm{i} \sum_s \frac{\omega_{{\rm p}s}^2}{\varpi^2} \left[2\sqrt{\rm \pi} \tilde{\varpi}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \tilde{v}_{s\bot}^2 \sum_{n ={-}\infty}^{\infty} \varXi_s(\zeta_{sn},\tilde{v}_{s\bot}) \boldsymbol{\mathsf{R}}_{sn}(\zeta_{sn},\tilde{v}_{s\bot}) \right] . \end{equation}
\begin{equation} \boldsymbol{\mathfrak{E}}^A ={-}\mathrm{i} \sum_s \frac{\omega_{{\rm p}s}^2}{\varpi^2} \left[2\sqrt{\rm \pi} \tilde{\varpi}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \tilde{v}_{s\bot}^2 \sum_{n ={-}\infty}^{\infty} \varXi_s(\zeta_{sn},\tilde{v}_{s\bot}) \boldsymbol{\mathsf{R}}_{sn}(\zeta_{sn},\tilde{v}_{s\bot}) \right] . \end{equation}We now consider stability conditions (E13) in turn.
First evaluating (E13c), it can be shown that
 \begin{align} \mathrm{i} \left(\mathfrak{E}_{xx}^{A} + \mathfrak{E}_{yy}^{A} + \mathfrak{E}_{zz}^{A}\right) &= 2\sqrt{\rm \pi} \sum_s \frac{\omega_{{\rm p}s}^2}{\varpi^2} \tilde{\varpi}_{s\|} \sum_{n ={-}\infty}^{\infty} \left\{\int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot}^2 \varXi_s(\zeta_{sn},\tilde{v}_{s\bot})\right. \nonumber\\ & \quad \left.\times\, \left[\frac{n^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{k_{\bot}^2 \tilde{\rho}_s^2 \tilde{v}_{s\bot}^2} + {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2+ \frac{\zeta_{sn}^2}{\tilde{v}_{s\bot}^2} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2\right] \vphantom{\int_0^{\infty} \mathrm{d}} \right\} . \end{align}
\begin{align} \mathrm{i} \left(\mathfrak{E}_{xx}^{A} + \mathfrak{E}_{yy}^{A} + \mathfrak{E}_{zz}^{A}\right) &= 2\sqrt{\rm \pi} \sum_s \frac{\omega_{{\rm p}s}^2}{\varpi^2} \tilde{\varpi}_{s\|} \sum_{n ={-}\infty}^{\infty} \left\{\int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot}^2 \varXi_s(\zeta_{sn},\tilde{v}_{s\bot})\right. \nonumber\\ & \quad \left.\times\, \left[\frac{n^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2}{k_{\bot}^2 \tilde{\rho}_s^2 \tilde{v}_{s\bot}^2} + {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2+ \frac{\zeta_{sn}^2}{\tilde{v}_{s\bot}^2} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2\right] \vphantom{\int_0^{\infty} \mathrm{d}} \right\} . \end{align}It is clear that the right-hand side (E16) is negative if
For a Maxwellian distribution,
and thus ![]() $\mathrm {i} (\mathfrak {E}_{xx}^{A}+\mathfrak {E}_{yy}^{A}+\mathfrak {E}_{zz}^{A}) < 0$, as required. For the CE distribution (2.72)
$\mathrm {i} (\mathfrak {E}_{xx}^{A}+\mathfrak {E}_{yy}^{A}+\mathfrak {E}_{zz}^{A}) < 0$, as required. For the CE distribution (2.72)
 \begin{align} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) & ={-} \tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \left\{2 + \eta_s \left[2 \tilde{v}_{s\|} A_s(\tilde{v}_s) - \frac{\tilde{v}_{s\|}}{\tilde{v}_s} A_s'(\tilde{v}_s) \right]\right. \nonumber\\ &\quad \left. +\, \epsilon_s \left[ 2 C_s(\tilde{v}_s) \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}+\frac{1}{2}\right) - \frac{1}{\tilde{v}_s} \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}\right)C_s'(\tilde{v}_s) \right] \right\} \nonumber\\ &\quad - \frac{\tilde{v}_{s\bot}}{ \tilde{\omega}_{s\|}} \exp \left(-\tilde{v}_{s}^2\right) \left[\eta_s A_s(\tilde{v}_s) - 3 \epsilon_s C_s(\tilde{v}_s) \tilde{v}_{s\|} \right] . \end{align}
\begin{align} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) & ={-} \tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \left\{2 + \eta_s \left[2 \tilde{v}_{s\|} A_s(\tilde{v}_s) - \frac{\tilde{v}_{s\|}}{\tilde{v}_s} A_s'(\tilde{v}_s) \right]\right. \nonumber\\ &\quad \left. +\, \epsilon_s \left[ 2 C_s(\tilde{v}_s) \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}+\frac{1}{2}\right) - \frac{1}{\tilde{v}_s} \left(\tilde{v}_{s\|}^2-\frac{\tilde{v}_{s\bot}^2}{2}\right)C_s'(\tilde{v}_s) \right] \right\} \nonumber\\ &\quad - \frac{\tilde{v}_{s\bot}}{ \tilde{\omega}_{s\|}} \exp \left(-\tilde{v}_{s}^2\right) \left[\eta_s A_s(\tilde{v}_s) - 3 \epsilon_s C_s(\tilde{v}_s) \tilde{v}_{s\|} \right] . \end{align}
For ![]() $|\tilde {\omega }_{s\|}| \gtrsim 1$, it is clear for
$|\tilde {\omega }_{s\|}| \gtrsim 1$, it is clear for ![]() $\tilde {v}_s \lesssim 1$ that the largest contribution to
$\tilde {v}_s \lesssim 1$ that the largest contribution to ![]() $\varXi _s(\tilde {v}_{s\|},\tilde {v}_{s\bot })$ comes from the Maxwellian term; the non-Maxwellian terms are
$\varXi _s(\tilde {v}_{s\|},\tilde {v}_{s\bot })$ comes from the Maxwellian term; the non-Maxwellian terms are ![]() ${O}(\eta _s,\epsilon _s)$. Thus, for
${O}(\eta _s,\epsilon _s)$. Thus, for ![]() $\zeta _{sn}, \tilde {v}_{s\bot } \lesssim 1$,
$\zeta _{sn}, \tilde {v}_{s\bot } \lesssim 1$, ![]() $\varXi _s(\zeta _{sn},\tilde {v}_{s\bot }) < 0$. As discussed in Appendix (D.4.2), for
$\varXi _s(\zeta _{sn},\tilde {v}_{s\bot }) < 0$. As discussed in Appendix (D.4.2), for ![]() $\zeta _{sn} \gg 1$, the sign of
$\zeta _{sn} \gg 1$, the sign of ![]() $\varXi _s(\zeta _{sn},\tilde {v}_{s\bot }) < 0$ can, in principle, be reversed. However, the magnitude of
$\varXi _s(\zeta _{sn},\tilde {v}_{s\bot }) < 0$ can, in principle, be reversed. However, the magnitude of ![]() $\varXi _s(\zeta _{sn},\tilde {v}_{s\bot })$ is exponentially small for such
$\varXi _s(\zeta _{sn},\tilde {v}_{s\bot })$ is exponentially small for such ![]() $\zeta _{sn}$, and thus so is
$\zeta _{sn}$, and thus so is ![]() $\varrho _2$.
$\varrho _2$.
The remaining conditions (E13a) and (E13b) are much more tedious to treat; thus for simplicity, we explicitly consider only the case when a single particle species provides the dominant contribution to the dielectric tensor. Under this assumption, it can be shown that
 \begin{align} &\mathfrak{E}_{xx}^{A} \mathfrak{E}_{yy}^{A} + \mathfrak{E}_{yy}^{A} \mathfrak{E}_{zz}^{A} + \mathfrak{E}_{zz}^{A} \mathfrak{E}_{xx}^{A} + (\mathfrak{E}_{xy}^{A})^2+(\mathfrak{E}_{yz}^{A})^2 + (\mathfrak{E}_{xz}^{A})^2 \nonumber\\ &\quad = 2 {\rm \pi}\frac{\omega_{{\rm p}s}^4}{\varpi^4} \tilde{\varpi}_{s\|}^2 \sum_{m ={-}\infty}^{\infty} \sum_{n ={-}\infty}^{\infty} \bigg\{ \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(1)} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(2)} \, \tilde{v}_{s\bot}^{(1)} \tilde{v}_{s\bot}^{(2)} \nonumber\\ & \qquad \left.\times \left[ \varXi_s(\zeta_{sm},\tilde{v}_{s\bot}^{(1)}) \varXi_s(\zeta_{sn},\tilde{v}_{s\bot}^{(2)}) \mathfrak{A}_{mn} \, (\alpha_s, \tilde{v}_{s\bot}^{(1)},\tilde{v}_{s\bot}^{(2)}) \right] \right\} , \end{align}
\begin{align} &\mathfrak{E}_{xx}^{A} \mathfrak{E}_{yy}^{A} + \mathfrak{E}_{yy}^{A} \mathfrak{E}_{zz}^{A} + \mathfrak{E}_{zz}^{A} \mathfrak{E}_{xx}^{A} + (\mathfrak{E}_{xy}^{A})^2+(\mathfrak{E}_{yz}^{A})^2 + (\mathfrak{E}_{xz}^{A})^2 \nonumber\\ &\quad = 2 {\rm \pi}\frac{\omega_{{\rm p}s}^4}{\varpi^4} \tilde{\varpi}_{s\|}^2 \sum_{m ={-}\infty}^{\infty} \sum_{n ={-}\infty}^{\infty} \bigg\{ \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(1)} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(2)} \, \tilde{v}_{s\bot}^{(1)} \tilde{v}_{s\bot}^{(2)} \nonumber\\ & \qquad \left.\times \left[ \varXi_s(\zeta_{sm},\tilde{v}_{s\bot}^{(1)}) \varXi_s(\zeta_{sn},\tilde{v}_{s\bot}^{(2)}) \mathfrak{A}_{mn} \, (\alpha_s, \tilde{v}_{s\bot}^{(1)},\tilde{v}_{s\bot}^{(2)}) \right] \right\} , \end{align}
where ![]() $\alpha _s \equiv k_{\bot } \tilde {\rho }_s$ and
$\alpha _s \equiv k_{\bot } \tilde {\rho }_s$ and
 \begin{align} &\mathfrak{A}_{mn}(\alpha_s,\tilde{v}_{s\bot}^{(1)},\tilde{v}_{s\bot}^{(2)}) \nonumber\\ &\quad \equiv \frac{1}{\alpha_s^2} \left[m \tilde{v}_{s\bot}^{(2)} {J}_m(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(2)}) - n \tilde{v}_{s\bot}^{(1)} {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n(\alpha_s \tilde{v}_{s\bot}^{(2)}) \right]^2 \nonumber\\ &\qquad + \frac{1}{\alpha_s^2} \left[m \zeta_{sn} \tilde{v}_{s\bot}^{(2)} {J}_m(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(2)}) - n \zeta_{sm} \tilde{v}_{s\bot}^{(1)} {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n(\alpha_s \tilde{v}_{s\bot}^{(2)}) \right]^2 \nonumber\\ &\qquad + \left[\zeta_{sn} \tilde{v}_{s\bot}^{(2)} {J}_m(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(2)}) - \zeta_{sm} \tilde{v}_{s\bot}^{(1)} {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n(\alpha_s \tilde{v}_{s\bot}^{(2)}) \right]^2 . \end{align}
\begin{align} &\mathfrak{A}_{mn}(\alpha_s,\tilde{v}_{s\bot}^{(1)},\tilde{v}_{s\bot}^{(2)}) \nonumber\\ &\quad \equiv \frac{1}{\alpha_s^2} \left[m \tilde{v}_{s\bot}^{(2)} {J}_m(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(2)}) - n \tilde{v}_{s\bot}^{(1)} {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n(\alpha_s \tilde{v}_{s\bot}^{(2)}) \right]^2 \nonumber\\ &\qquad + \frac{1}{\alpha_s^2} \left[m \zeta_{sn} \tilde{v}_{s\bot}^{(2)} {J}_m(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(2)}) - n \zeta_{sm} \tilde{v}_{s\bot}^{(1)} {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n(\alpha_s \tilde{v}_{s\bot}^{(2)}) \right]^2 \nonumber\\ &\qquad + \left[\zeta_{sn} \tilde{v}_{s\bot}^{(2)} {J}_m(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(2)}) - \zeta_{sm} \tilde{v}_{s\bot}^{(1)} {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(1)}) {J}_n(\alpha_s \tilde{v}_{s\bot}^{(2)}) \right]^2 . \end{align}
Being a sum of positive terms, ![]() $\mathfrak {A}_{mn}$ is positive for all
$\mathfrak {A}_{mn}$ is positive for all ![]() $n$ and
$n$ and ![]() $m$, and thus we again conclude that the integrand on the right-hand side of (E20) is negative if
$m$, and thus we again conclude that the integrand on the right-hand side of (E20) is negative if ![]() $\varXi _s(\zeta _{sm},\tilde {v}_{s\bot }) < 0$ and
$\varXi _s(\zeta _{sm},\tilde {v}_{s\bot }) < 0$ and ![]() $\varXi _s(\zeta _{sn},\tilde {v}_{s\bot }) < 0$. Via similar reasoning to that applied to
$\varXi _s(\zeta _{sn},\tilde {v}_{s\bot }) < 0$. Via similar reasoning to that applied to ![]() $\varrho _2$ in the previous paragraph, it follows that for the CE distribution function, the only way in which this condition can be violated is for either
$\varrho _2$ in the previous paragraph, it follows that for the CE distribution function, the only way in which this condition can be violated is for either ![]() $\zeta _{sm} \gg 1$ or
$\zeta _{sm} \gg 1$ or ![]() $\zeta _{sn} \gg 1$ – both of which give rise to exponentially small terms. Thus, either
$\zeta _{sn} \gg 1$ – both of which give rise to exponentially small terms. Thus, either ![]() $\varrho _1 > 0$ or
$\varrho _1 > 0$ or ![]() $\varrho _1$ is exponentially small in
$\varrho _1$ is exponentially small in ![]() $\eta _s$ and
$\eta _s$ and ![]() $\epsilon _s$.
$\epsilon _s$.
Finally, for (E13a), it is necessary to evaluate ![]() $\mbox {det}\, \boldsymbol {\mathfrak {E}}^{A}$; this becomes (after much tedious algebra)
$\mbox {det}\, \boldsymbol {\mathfrak {E}}^{A}$; this becomes (after much tedious algebra)
 \begin{align} \mbox{det}\,\boldsymbol{\mathfrak{E}}^{A}& ={-}\frac{4}{3} \mathrm{i} {\rm \pi}^{3/2} \frac{\omega_{{\rm p}s}^6}{\varpi^6} \tilde{\varpi}_{s\|}^3 \nonumber\\ &\quad \times \sum_{m ={-}\infty}^{\infty} \sum_{n ={-}\infty}^{\infty} \sum_{l ={-}\infty}^{\infty} \left\{ \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(1)} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(2)} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(3)} \, \tilde{v}_{s\bot}^{(1)} \tilde{v}_{s\bot}^{(2)} \tilde{v}_{s\bot}^{(3)}\right. \nonumber\\ &\quad \left.\times\, \left[\varXi_s(\zeta_{sm},\tilde{v}_{s\bot}^{(1)}) \varXi_s(\zeta_{sn},\tilde{v}_{s\bot}^{(2)}) \varXi_s(\zeta_{sl},\tilde{v}_{s\bot}^{(3)}) \mathfrak{B}_{mnl} \, (\alpha_s,\tilde{v}_{s\bot}^{(1)},\tilde{v}_{s\bot}^{(2)},\tilde{v}_{s\bot}^{(3)}) \right] \vphantom{\int_0^{\infty} \mathrm{d} }\right\}, \end{align}
\begin{align} \mbox{det}\,\boldsymbol{\mathfrak{E}}^{A}& ={-}\frac{4}{3} \mathrm{i} {\rm \pi}^{3/2} \frac{\omega_{{\rm p}s}^6}{\varpi^6} \tilde{\varpi}_{s\|}^3 \nonumber\\ &\quad \times \sum_{m ={-}\infty}^{\infty} \sum_{n ={-}\infty}^{\infty} \sum_{l ={-}\infty}^{\infty} \left\{ \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(1)} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(2)} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}^{(3)} \, \tilde{v}_{s\bot}^{(1)} \tilde{v}_{s\bot}^{(2)} \tilde{v}_{s\bot}^{(3)}\right. \nonumber\\ &\quad \left.\times\, \left[\varXi_s(\zeta_{sm},\tilde{v}_{s\bot}^{(1)}) \varXi_s(\zeta_{sn},\tilde{v}_{s\bot}^{(2)}) \varXi_s(\zeta_{sl},\tilde{v}_{s\bot}^{(3)}) \mathfrak{B}_{mnl} \, (\alpha_s,\tilde{v}_{s\bot}^{(1)},\tilde{v}_{s\bot}^{(2)},\tilde{v}_{s\bot}^{(3)}) \right] \vphantom{\int_0^{\infty} \mathrm{d} }\right\}, \end{align}where
 \begin{align} &\mathfrak{B}_{mnl}(\alpha_s,\tilde{v}_{s\bot}^{(1)},\tilde{v}_{s\bot}^{(2)},\tilde{v}_{s\bot}^{(3)}) \nonumber\\ &\quad \equiv \left\{m {J}_m(\alpha_s \tilde{v}_{s\bot}^{(1)})\left[\tilde{v}_{s\bot}^{(1)} \zeta_{sn} {J}_n(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_l'(\alpha_s \tilde{v}_{s\bot}^{(3)}) - \tilde{v}_{s\bot}^{(3)} \zeta_{sl} {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_l(\alpha_s \tilde{v}_{s\bot}^{(3)}) \right]\right. \nonumber\\ &\qquad + n {J}_n(\alpha_s \tilde{v}_{s\bot}^{(1)})\left[\tilde{v}_{s\bot}^{(2)} \zeta_{sl} {J}_l(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(3)}) - \tilde{v}_{s\bot}^{(1)} \zeta_{sm} {J}_l'(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_m(\alpha_s \tilde{v}_{s\bot}^{(3)}) \right] \nonumber\\ & \qquad\left. +\, l {J}_l(\alpha_s \tilde{v}_{s\bot}^{(1)})\left[\tilde{v}_{s\bot}^{(3)} \zeta_{sm} {J}_m(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(3)}) - \tilde{v}_{s\bot}^{(2)} \zeta_{sn} {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_n(\alpha_s \tilde{v}_{s\bot}^{(3)}) \right] \right\}^2 . \end{align}
\begin{align} &\mathfrak{B}_{mnl}(\alpha_s,\tilde{v}_{s\bot}^{(1)},\tilde{v}_{s\bot}^{(2)},\tilde{v}_{s\bot}^{(3)}) \nonumber\\ &\quad \equiv \left\{m {J}_m(\alpha_s \tilde{v}_{s\bot}^{(1)})\left[\tilde{v}_{s\bot}^{(1)} \zeta_{sn} {J}_n(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_l'(\alpha_s \tilde{v}_{s\bot}^{(3)}) - \tilde{v}_{s\bot}^{(3)} \zeta_{sl} {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_l(\alpha_s \tilde{v}_{s\bot}^{(3)}) \right]\right. \nonumber\\ &\qquad + n {J}_n(\alpha_s \tilde{v}_{s\bot}^{(1)})\left[\tilde{v}_{s\bot}^{(2)} \zeta_{sl} {J}_l(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(3)}) - \tilde{v}_{s\bot}^{(1)} \zeta_{sm} {J}_l'(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_m(\alpha_s \tilde{v}_{s\bot}^{(3)}) \right] \nonumber\\ & \qquad\left. +\, l {J}_l(\alpha_s \tilde{v}_{s\bot}^{(1)})\left[\tilde{v}_{s\bot}^{(3)} \zeta_{sm} {J}_m(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_n'(\alpha_s \tilde{v}_{s\bot}^{(3)}) - \tilde{v}_{s\bot}^{(2)} \zeta_{sn} {J}_m'(\alpha_s \tilde{v}_{s\bot}^{(2)}) {J}_n(\alpha_s \tilde{v}_{s\bot}^{(3)}) \right] \right\}^2 . \end{align}
Similarly to ![]() $\mathfrak {A}_{mn}$,
$\mathfrak {A}_{mn}$, ![]() $\mathfrak {B}_{mnl}$ is strictly positive for all
$\mathfrak {B}_{mnl}$ is strictly positive for all ![]() $m$,
$m$, ![]() $n$ and
$n$ and ![]() $l$, meaning that the integrand on the right-hand side of (E22) is negative if
$l$, meaning that the integrand on the right-hand side of (E22) is negative if ![]() $\varXi _s(\zeta _{sm},\tilde {v}_{s\bot }) < 0$,
$\varXi _s(\zeta _{sm},\tilde {v}_{s\bot }) < 0$, ![]() $\varXi _s(\zeta _{sn},\tilde {v}_{s\bot }) < 0$ and
$\varXi _s(\zeta _{sn},\tilde {v}_{s\bot }) < 0$ and ![]() $\varXi _s(\zeta _{sl},\tilde {v}_{s\bot }) < 0$. For the CE distribution, exactly the same argument as before applies to show that either
$\varXi _s(\zeta _{sl},\tilde {v}_{s\bot }) < 0$. For the CE distribution, exactly the same argument as before applies to show that either ![]() $\varrho _0 > 0$ or it is exponentially small.
$\varrho _0 > 0$ or it is exponentially small.
In summary, we have now verified that the only situation in which the stability conditions (E13) are not satisfied are those for which ![]() $\varrho _0$,
$\varrho _0$, ![]() $\varrho _1$ and
$\varrho _1$ and ![]() $\varrho _2$ are exponentially small in
$\varrho _2$ are exponentially small in ![]() $\eta _s$ and
$\eta _s$ and ![]() $\epsilon _s$. In the latter case, considerations of bounds (E9a–c) and (E10) implies that
$\epsilon _s$. In the latter case, considerations of bounds (E9a–c) and (E10) implies that ![]() $\varsigma _a$,
$\varsigma _a$, ![]() $\varsigma _b$, and
$\varsigma _b$, and ![]() $\varsigma _c$ are also all exponentially small in
$\varsigma _c$ are also all exponentially small in ![]() $\eta _s$ and
$\eta _s$ and ![]() $\epsilon _s$. The claim of the appendix follows.
$\epsilon _s$. The claim of the appendix follows.
Appendix F. Properties of leading-order expansion  $\boldsymbol {\mathfrak {E}}^{(0)}$ of dielectric tensor (2.74) in
$\boldsymbol {\mathfrak {E}}^{(0)}$ of dielectric tensor (2.74) in  $\tilde {\omega }_{s\|} \ll 1$ for a weakly anisotropic distribution function
$\tilde {\omega }_{s\|} \ll 1$ for a weakly anisotropic distribution function
F.1. Symmetries of  $\boldsymbol {\mathfrak {E}}_s^{(0)}$ in coordinate basis
$\boldsymbol {\mathfrak {E}}_s^{(0)}$ in coordinate basis  $\{\hat {x},\hat {y},\hat {z}\}$
$\{\hat {x},\hat {y},\hat {z}\}$
In this appendix, we show that the leading-order expansion ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$ (cf. (2.100a)) of the dielectric tensor
$\boldsymbol {\mathfrak {E}}_s^{(0)}$ (cf. (2.100a)) of the dielectric tensor ![]() $\boldsymbol {\mathfrak {E}}_s$ of species
$\boldsymbol {\mathfrak {E}}_s$ of species ![]() $s$ (cf. (2.96)) in
$s$ (cf. (2.96)) in ![]() $\tilde {\omega }_{s\|} \ll 1$ arising in a non-relativistic plasma with only weak anisotropy of its particle distribution function obeys additional symmetries (2.101), viz.
$\tilde {\omega }_{s\|} \ll 1$ arising in a non-relativistic plasma with only weak anisotropy of its particle distribution function obeys additional symmetries (2.101), viz.
 $$\begin{gather}(\boldsymbol{\mathfrak{E}}_s^{(0)})_{zz} = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} , \end{gather}$$
$$\begin{gather}(\boldsymbol{\mathfrak{E}}_s^{(0)})_{zz} = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} , \end{gather}$$
when ![]() $k \rho _s \sim 1$. The term ‘weak anisotropy’ means that the magnitude of angular anisotropy – mathematically represented by the function
$k \rho _s \sim 1$. The term ‘weak anisotropy’ means that the magnitude of angular anisotropy – mathematically represented by the function ![]() $\varLambda _s$ defined by (2.84) – satisfies
$\varLambda _s$ defined by (2.84) – satisfies ![]() $\varLambda _s \lesssim \tilde {\omega }_{s\|}$ for all particle species when
$\varLambda _s \lesssim \tilde {\omega }_{s\|}$ for all particle species when ![]() $\tilde {v}_s \sim 1$.
$\tilde {v}_s \sim 1$.
We begin the proof by substituting (2.77) into (2.96) to give
 \begin{align} \boldsymbol{\mathfrak{E}}_s & \equiv \frac{\omega_{{\rm p}s}^2}{\omega^2} \left[ \vphantom{\sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{v}_{s\|}}} \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}}{|k_{\|}|} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \hat{\boldsymbol{z}} \hat{\boldsymbol{z}}\right. \nonumber\\ &\quad \left.+\, \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{v}_{s\|}} \right] . \end{align}
\begin{align} \boldsymbol{\mathfrak{E}}_s & \equiv \frac{\omega_{{\rm p}s}^2}{\omega^2} \left[ \vphantom{\sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{v}_{s\|}}} \frac{2}{\sqrt{\rm \pi}} \frac{k_{\|}}{|k_{\|}|} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \hat{\boldsymbol{z}} \hat{\boldsymbol{z}}\right. \nonumber\\ &\quad \left.+\, \tilde{\omega}_{s\|} \frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n ={-}\infty}^{\infty} \frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn} -\tilde{v}_{s\|}} \right] . \end{align}
Then, under the assumed ordering ![]() $\tilde {\omega }_{s\|} \sim \varLambda _s$, the function
$\tilde {\omega }_{s\|} \sim \varLambda _s$, the function ![]() $\varXi _s$ defined by (2.85) satisfies
$\varXi _s$ defined by (2.85) satisfies ![]() $\varXi _s \sim 1$ for
$\varXi _s \sim 1$ for ![]() $\tilde {v}_s \sim 1$; therefore,
$\tilde {v}_s \sim 1$; therefore, ![]() $\boldsymbol {\mathfrak {E}}_s$ has order-unity elements as
$\boldsymbol {\mathfrak {E}}_s$ has order-unity elements as ![]() $\tilde {\omega }_{s\|} \rightarrow 0$. Let us expand
$\tilde {\omega }_{s\|} \rightarrow 0$. Let us expand ![]() $\boldsymbol {\mathfrak {E}}_s$ in a Taylor series around
$\boldsymbol {\mathfrak {E}}_s$ in a Taylor series around ![]() $\tilde {\omega }_{s\|} = 0$:
$\tilde {\omega }_{s\|} = 0$:
where ![]() $\delta \boldsymbol {\mathfrak {E}}_s = {O}(\tilde {\omega }_{s\|}^2)$, and the matrix elements of
$\delta \boldsymbol {\mathfrak {E}}_s = {O}(\tilde {\omega }_{s\|}^2)$, and the matrix elements of ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$ are given below:
$\boldsymbol {\mathfrak {E}}_s^{(0)}$ are given below:
 \begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{xx} & \equiv{-}\frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s}\right. \nonumber\\ & \quad \times \left. \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right] , \end{align}
\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{xx} & \equiv{-}\frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s}\right. \nonumber\\ & \quad \times \left. \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right] , \end{align} \begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{xy} & \equiv{-}\frac{2 \mathrm{i} \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}|\tilde{\rho}_s} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \right] , \end{align}
\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{xy} & \equiv{-}\frac{2 \mathrm{i} \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}|\tilde{\rho}_s} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \right] , \end{align} \begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{xz} & \equiv{-}\frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \,\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s}\right. \nonumber\\ & \quad \left. \times\, \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right], \end{align}
\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{xz} & \equiv{-}\frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \,\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s}\right. \nonumber\\ & \quad \left. \times\, \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\, \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right], \end{align} \begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{yy} & \equiv{-}\frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s}\right. \nonumber\\ & \quad \left.\times\, \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right] , \end{align}
\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{yy} & \equiv{-}\frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s}\right. \nonumber\\ & \quad \left.\times\, \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right] , \end{align} \begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{yz} & \equiv{-}\frac{2 \mathrm{i} \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}\,\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \right] , \end{align}
\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{yz} & \equiv{-}\frac{2 \mathrm{i} \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}\,\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \right] , \end{align} \begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{zz} & \equiv \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \tilde{\omega}_{s\|} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \,\tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \nonumber\\ & \quad - \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \int_{C_L} \frac{\tilde{v}_{s\|}^2 \,\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 . \end{align}
\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)} )_{zz} & \equiv \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \tilde{\omega}_{s\|} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \,\tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \nonumber\\ & \quad - \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \int_{C_L} \frac{\tilde{v}_{s\|}^2 \,\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 . \end{align}Next, noting that
as well as
 \begin{equation} \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 = 0, \end{equation}
\begin{equation} \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 = 0, \end{equation}we see that the double integral in (F4c) can be rearranged to give
 \begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xz} & = \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{ |k_{\|}| k_{\bot} \tilde{\rho}_s^2}\int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s}\right. \nonumber\\ & \quad \left.\times\, \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right] ,\nonumber\\ & ={-}\frac{k_{\bot}}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} . \end{align}
\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xz} & = \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{ |k_{\|}| k_{\bot} \tilde{\rho}_s^2}\int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s}\right. \nonumber\\ & \quad \left.\times\, \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}\,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right] ,\nonumber\\ & ={-}\frac{k_{\bot}}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} . \end{align}Similarly, it can be shown that
 \begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{yz} & = \frac{2 \mathrm{i} \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{|k_{\|}| \tilde{\rho}_s} \int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \right] , \nonumber\\ & = \frac{k_{\bot}}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} . \end{align}
\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{yz} & = \frac{2 \mathrm{i} \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{|k_{\|}| \tilde{\rho}_s} \int_{C_L} \frac{\mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} \varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \right] , \nonumber\\ & = \frac{k_{\bot}}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} . \end{align}
Finally, ![]() $(\boldsymbol {\mathfrak {E}}_s^{(0)})_{zz}$ can also be written in terms of
$(\boldsymbol {\mathfrak {E}}_s^{(0)})_{zz}$ can also be written in terms of ![]() $(\boldsymbol {\mathfrak {E}}_s^{(0)})_{xx}$: because
$(\boldsymbol {\mathfrak {E}}_s^{(0)})_{xx}$: because
 \begin{equation} \frac{\tilde{v}_{s\|}^2}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} = \tilde{v}_{s\|} - \frac{n}{|k_{\|}| \tilde{\rho}_s} + \frac{n^2}{|k_{\|}| ^2\tilde{\rho}_s^2} \frac{1}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} , \end{equation}
\begin{equation} \frac{\tilde{v}_{s\|}^2}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} = \tilde{v}_{s\|} - \frac{n}{|k_{\|}| \tilde{\rho}_s} + \frac{n^2}{|k_{\|}| ^2\tilde{\rho}_s^2} \frac{1}{\tilde{v}_{s\|}+n/|k_{\|}| \tilde{\rho}_s} , \end{equation}it follows that
 \begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{zz} & = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} +\frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \tilde{\omega}_{s\|} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \,\tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \nonumber\\ & \quad - \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \int_{-\infty}^{\infty} \tilde{v}_{s\|} \,\mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \nonumber\\ & \quad + \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \nonumber\\ & = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} - \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\|} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \nonumber\\ & \quad + \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \tilde{\omega}_{s\|} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \,\tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \left[1-\sum_{n={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right] \nonumber\\ & = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} + \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) , \end{align}
\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{zz} & = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} +\frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \tilde{\omega}_{s\|} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \,\tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \nonumber\\ & \quad - \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \int_{-\infty}^{\infty} \tilde{v}_{s\|} \,\mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \nonumber\\ & \quad + \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \nonumber\\ & = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} - \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\|} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} \nonumber\\ & \quad + \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \tilde{\omega}_{s\|} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \,\tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \left[1-\sum_{n={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \right] \nonumber\\ & = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} + \frac{2 \omega_{{\rm p}s}^2}{\sqrt{\rm \pi} \omega^2} \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) , \end{align}where we have used the identity
 \begin{equation} \sum_{n={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 = 1 . \end{equation}
\begin{equation} \sum_{n={-}\infty}^{\infty} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 = 1 . \end{equation}Thus, we conclude that since the anisotropy is assumed small,
 \begin{equation} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{zz} = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} + {O}(\tilde{\omega}_{s\|}) , \end{equation}
\begin{equation} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{zz} = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} + {O}(\tilde{\omega}_{s\|}) , \end{equation}completing the proof.
F.2. Evaluating the dielectric tensor in coordinate basis  $\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$
$\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$
To demonstrate that the components of the dielectric tensor ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$ are given by (2.104), viz.
$\boldsymbol {\mathfrak {E}}_s^{(0)}$ are given by (2.104), viz.
 $$\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{11} &= \frac{k^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} , \end{align}$$
$$\begin{align} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{11} &= \frac{k^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} , \end{align}$$
we use (F1) to express ![]() $\boldsymbol {\mathfrak {E}_s}^{\!(0)}$ in the form
$\boldsymbol {\mathfrak {E}_s}^{\!(0)}$ in the form
 \begin{align} \boldsymbol{\mathfrak{E}}_s^{(0)} & = (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \hat{\boldsymbol{x}} \hat{\boldsymbol{x}} + (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} \left(\hat{\boldsymbol{x}} \hat{\boldsymbol{y}} -\hat{\boldsymbol{y}} \hat{\boldsymbol{x}}\right) + (\boldsymbol{\mathfrak{E}}_s^{(0)})_{yy} \hat{\boldsymbol{y}} \hat{\boldsymbol{y}} \nonumber\\ &\quad - \frac{k_{\bot}}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \left(\hat{\boldsymbol{x}} \hat{\boldsymbol{z}} +\hat{\boldsymbol{z}} \hat{\boldsymbol{x}}\right) + \frac{k_{\bot}}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} \left(\hat{\boldsymbol{y}} \hat{\boldsymbol{z}} -\hat{\boldsymbol{z}} \hat{\boldsymbol{y}}\right) + \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \hat{\boldsymbol{z}} \hat{\boldsymbol{z}} . \end{align}
\begin{align} \boldsymbol{\mathfrak{E}}_s^{(0)} & = (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \hat{\boldsymbol{x}} \hat{\boldsymbol{x}} + (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} \left(\hat{\boldsymbol{x}} \hat{\boldsymbol{y}} -\hat{\boldsymbol{y}} \hat{\boldsymbol{x}}\right) + (\boldsymbol{\mathfrak{E}}_s^{(0)})_{yy} \hat{\boldsymbol{y}} \hat{\boldsymbol{y}} \nonumber\\ &\quad - \frac{k_{\bot}}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \left(\hat{\boldsymbol{x}} \hat{\boldsymbol{z}} +\hat{\boldsymbol{z}} \hat{\boldsymbol{x}}\right) + \frac{k_{\bot}}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} \left(\hat{\boldsymbol{y}} \hat{\boldsymbol{z}} -\hat{\boldsymbol{z}} \hat{\boldsymbol{y}}\right) + \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \hat{\boldsymbol{z}} \hat{\boldsymbol{z}} . \end{align}Noting that
we can rewrite (F14) as
 \begin{align} \boldsymbol{\mathfrak{E}}_s^{(0)} & = \frac{k^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \left(\hat{\boldsymbol{y}} \times \hat{\boldsymbol{k}}\right)\left(\hat{\boldsymbol{y}} \times \hat{\boldsymbol{k}}\right) \nonumber\\ &\quad + \frac{k}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} \left[ \left(\hat{\boldsymbol{y}} \times \hat{\boldsymbol{k}}\right)\hat{\boldsymbol{y}} -\hat{\boldsymbol{y}} \left(\hat{\boldsymbol{y}} \times \hat{\boldsymbol{k}}\right)\right] + (\boldsymbol{\mathfrak{E}}_s^{(0)})_{yy}\hat{\boldsymbol{y}} \hat{\boldsymbol{y}} \end{align}
\begin{align} \boldsymbol{\mathfrak{E}}_s^{(0)} & = \frac{k^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \left(\hat{\boldsymbol{y}} \times \hat{\boldsymbol{k}}\right)\left(\hat{\boldsymbol{y}} \times \hat{\boldsymbol{k}}\right) \nonumber\\ &\quad + \frac{k}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} \left[ \left(\hat{\boldsymbol{y}} \times \hat{\boldsymbol{k}}\right)\hat{\boldsymbol{y}} -\hat{\boldsymbol{y}} \left(\hat{\boldsymbol{y}} \times \hat{\boldsymbol{k}}\right)\right] + (\boldsymbol{\mathfrak{E}}_s^{(0)})_{yy}\hat{\boldsymbol{y}} \hat{\boldsymbol{y}} \end{align} \begin{align} & = \frac{k^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \boldsymbol{e}_1 \boldsymbol{e}_1 + \frac{k}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} \left(\boldsymbol{e}_1 \boldsymbol{e}_2 - \boldsymbol{e}_2 \boldsymbol{e}_1 \right) + (\boldsymbol{\mathfrak{E}}_s^{(0)})_{yy} \boldsymbol{e}_2 \boldsymbol{e}_2 , \end{align}
\begin{align} & = \frac{k^2}{k_{\|}^2} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xx} \boldsymbol{e}_1 \boldsymbol{e}_1 + \frac{k}{|k_{\|}|} (\boldsymbol{\mathfrak{E}}_s^{(0)})_{xy} \left(\boldsymbol{e}_1 \boldsymbol{e}_2 - \boldsymbol{e}_2 \boldsymbol{e}_1 \right) + (\boldsymbol{\mathfrak{E}}_s^{(0)})_{yy} \boldsymbol{e}_2 \boldsymbol{e}_2 , \end{align}
leading to the desired results (F13). In addition, we see that ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)} \cdot \hat {\boldsymbol {k}} = 0$; thus, the results (2.105) claiming that certain components of
$\boldsymbol {\mathfrak {E}}_s^{(0)} \cdot \hat {\boldsymbol {k}} = 0$; thus, the results (2.105) claiming that certain components of ![]() $\boldsymbol {\mathfrak {E}}_s$ are small in
$\boldsymbol {\mathfrak {E}}_s$ are small in ![]() $\tilde {\omega }_{s\|}$ are justified.
$\tilde {\omega }_{s\|}$ are justified.
Appendix G. Dielectric tensor components for the CE distribution function (2.8)
In this appendix, we calculate the components of the dielectric tensor arising from the CE distribution function (2.8), with isotropic functions ![]() $A_e^T(\tilde {v}_e)$,
$A_e^T(\tilde {v}_e)$, ![]() $A_e^R(\tilde {v}_e)$,
$A_e^R(\tilde {v}_e)$, ![]() $A_e^u(\tilde {v}_e)$,
$A_e^u(\tilde {v}_e)$, ![]() $C_e(\tilde {v}_e)$,
$C_e(\tilde {v}_e)$, ![]() $A_i(\tilde {v}_i)$ and
$A_i(\tilde {v}_i)$ and ![]() $C_i(\tilde {v}_i)$ chosen as appropriate for a Krook collision operator (see Appendix B.2.1), viz.
$C_i(\tilde {v}_i)$ chosen as appropriate for a Krook collision operator (see Appendix B.2.1), viz.
This, via (2.108), allows for the dielectric tensor ![]() $\boldsymbol {\mathfrak {E}}_s$ to be calculated order by order in
$\boldsymbol {\mathfrak {E}}_s$ to be calculated order by order in ![]() $\tilde {\omega }_{s\|}$. We carry out these calculations in the case of non-relativistic fluctuations, and so
$\tilde {\omega }_{s\|}$. We carry out these calculations in the case of non-relativistic fluctuations, and so
where we remind the reader that (cf. (F2))
 $$\begin{align}
\boldsymbol{\mathfrak{E}}_s &= \frac{\omega_{{\rm
p}s}^2}{\omega^2} \left[ \vphantom{\sum_{n
={-}\infty}^{\infty}
\frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn}
-\tilde{v}_{s\|}} } \frac{2}{\sqrt{\rm \pi}}
\frac{k_{\|}}{|k_{\|}|} \int_{-\infty}^{\infty} \mathrm{d}
\tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty}
\mathrm{d} \tilde{v}_{s\bot}
\,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot})
\hat{\boldsymbol{z}} \hat{\boldsymbol{z}}\right.
\nonumber\\ &\quad \left.+ \tilde{\omega}_{s\|}
\frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|}
\int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}
\,\tilde{v}_{s\bot}^2
\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n
={-}\infty}^{\infty}
\frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn}
-\tilde{v}_{s\|}} \right] ,
\end{align}$$
$$\begin{align}
\boldsymbol{\mathfrak{E}}_s &= \frac{\omega_{{\rm
p}s}^2}{\omega^2} \left[ \vphantom{\sum_{n
={-}\infty}^{\infty}
\frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn}
-\tilde{v}_{s\|}} } \frac{2}{\sqrt{\rm \pi}}
\frac{k_{\|}}{|k_{\|}|} \int_{-\infty}^{\infty} \mathrm{d}
\tilde{v}_{s\|} \, \tilde{v}_{s\|} \int_0^{\infty}
\mathrm{d} \tilde{v}_{s\bot}
\,\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot})
\hat{\boldsymbol{z}} \hat{\boldsymbol{z}}\right.
\nonumber\\ &\quad \left.+ \tilde{\omega}_{s\|}
\frac{2}{\sqrt{\rm \pi}} \int_{C_L} \mathrm{d} \tilde{v}_{s\|}
\int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot}
\,\tilde{v}_{s\bot}^2
\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \sum_{n
={-}\infty}^{\infty}
\frac{\boldsymbol{\mathsf{R}}_{sn}}{\zeta_{sn}
-\tilde{v}_{s\|}} \right] ,
\end{align}$$ $$\begin{gather}\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \equiv \tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}}-\tilde{v}_{s\|} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} , \end{gather}$$
$$\begin{gather}\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \equiv \tilde{v}_{s\bot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\|}}-\tilde{v}_{s\|} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} , \end{gather}$$ $$\begin{gather}\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \equiv \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} + \frac{\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot})}{\tilde{\omega}_{s\|}} , \end{gather}$$
$$\begin{gather}\varXi_s(\tilde{v}_{s\|},\tilde{v}_{s\bot}) \equiv \frac{\partial \tilde{f}_{s0}}{\partial \tilde{v}_{s\bot}} + \frac{\varLambda_s(\tilde{v}_{s\|},\tilde{v}_{s\bot})}{\tilde{\omega}_{s\|}} , \end{gather}$$and
 $$\begin{align}(\boldsymbol{\mathsf{R}}_{sn} )_{zz} &\equiv \frac{\tilde{v}_{s\|}^2}{\tilde{v}_{s\bot}^2} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 . \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{R}}_{sn} )_{zz} &\equiv \frac{\tilde{v}_{s\|}^2}{\tilde{v}_{s\bot}^2} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 . \end{align}$$
The components of the dielectric tensor ![]() $\boldsymbol {\mathfrak {E}}_s$ in coordinate basis
$\boldsymbol {\mathfrak {E}}_s$ in coordinate basis ![]() $\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$ are related to the components in coordinate basis
$\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$ are related to the components in coordinate basis ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ by
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ by
 $$\begin{align}(\boldsymbol{\mathfrak{E}}_s)_{13} &= \frac{k_{\|} k_{\bot}}{k^2} \left[(\boldsymbol{\mathfrak{E}}_s)_{xx} - (\boldsymbol{\mathfrak{E}}_s)_{zz}\right] + \left(\frac{k_{\|}^2}{k^2}- \frac{k_{\bot}^2}{k^2}\right) (\boldsymbol{\mathfrak{E}}_s)_{xz} , \end{align}$$
$$\begin{align}(\boldsymbol{\mathfrak{E}}_s)_{13} &= \frac{k_{\|} k_{\bot}}{k^2} \left[(\boldsymbol{\mathfrak{E}}_s)_{xx} - (\boldsymbol{\mathfrak{E}}_s)_{zz}\right] + \left(\frac{k_{\|}^2}{k^2}- \frac{k_{\bot}^2}{k^2}\right) (\boldsymbol{\mathfrak{E}}_s)_{xz} , \end{align}$$
For clarity, we calculate separately the Maxwellian contribution ![]() $\boldsymbol{\mathsf{M}}_s$ of the total CE distribution function and the non-Maxwellian contribution
$\boldsymbol{\mathsf{M}}_s$ of the total CE distribution function and the non-Maxwellian contribution ![]() $\boldsymbol{\mathsf{P}}_s$ associated with the CE electron friction, temperature-gradient and shear terms to
$\boldsymbol{\mathsf{P}}_s$ associated with the CE electron friction, temperature-gradient and shear terms to ![]() $\boldsymbol {\mathfrak {E}}_s$ – viz. we decompose
$\boldsymbol {\mathfrak {E}}_s$ – viz. we decompose ![]() $\boldsymbol {\mathfrak {E}}_s$ as follows (cf. (2.97)):
$\boldsymbol {\mathfrak {E}}_s$ as follows (cf. (2.97)):
G.1. Maxwellian distribution
G.1.1. General dielectric tensor
Consider a non-dimensionalised Maxwellian distribution function
The Maxwellian is isotropic, so (G6) gives
while (G7) becomes
Substituting this into (G3) gives
 \begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} & = \frac{4}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} & = \frac{4}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{xy} & = \frac{4 \mathrm{i}}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xy} & = \frac{4 \mathrm{i}}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{xz} & = \frac{4}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}\right. \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xz} & = \frac{4}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}\right. \end{align} \begin{align} & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] , \end{align}
\begin{align} & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} & = \frac{4}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^3 {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} & = \frac{4}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^3 {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} & ={-}\frac{4 \mathrm{i}}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} & ={-}\frac{4 \mathrm{i}}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{zz} & = \frac{4}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] . \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{zz} & = \frac{4}{\sqrt{\rm \pi}} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] . \end{align}Using the integral identities
involving the plasma dispersion function, and the identities
 \begin{align} \int_0^{\infty}
\mathrm{d} t \, t^3 {J}_n'(\alpha t)^2 \exp
\left({-}t^2\right) &= \frac{1}{4} \exp
\left(-\frac{\alpha^2}{2}\right)\left\{\frac{2n^2}{\alpha^2}
{I}_n\!\left(\frac{\alpha^2}{2}\right) \right.
\nonumber\\ &\left. \quad - \alpha^2 \left[{I}_n'\!\left(\frac{\alpha^2}{2}\right)-{I}_n\!\left(\frac{\alpha^2}{2}\right)\right] \right\} ,
\end{align}
\begin{align} \int_0^{\infty}
\mathrm{d} t \, t^3 {J}_n'(\alpha t)^2 \exp
\left({-}t^2\right) &= \frac{1}{4} \exp
\left(-\frac{\alpha^2}{2}\right)\left\{\frac{2n^2}{\alpha^2}
{I}_n\!\left(\frac{\alpha^2}{2}\right) \right.
\nonumber\\ &\left. \quad - \alpha^2 \left[{I}_n'\!\left(\frac{\alpha^2}{2}\right)-{I}_n\!\left(\frac{\alpha^2}{2}\right)\right] \right\} ,
\end{align}
involving Bessel functions (here ![]() $\alpha$ is a real number), we obtain expressions for the dielectric components (G14) in terms of special functions:
$\alpha$ is a real number), we obtain expressions for the dielectric components (G14) in terms of special functions:
 $$\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} &= 2\tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} Z\!\left(\zeta_{sn}\right) \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} &= 2\tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} Z\!\left(\zeta_{sn}\right) \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$ $$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xy} &= \mathrm{i} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} n Z\!\left(\zeta_{sn}\right) \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xy} &= \mathrm{i} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} n Z\!\left(\zeta_{sn}\right) \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}$$ $$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xz} &= 2 \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xz} &= 2 \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$ \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} &= \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} Z\!\left(\zeta_{sn}\right) \nonumber\\ &\quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} &= \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} Z\!\left(\zeta_{sn}\right) \nonumber\\ &\quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} & ={-}\mathrm{i} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} & ={-}\mathrm{i} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} $$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{zz} &= 2 \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \zeta_{sn} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{zz} &= 2 \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \zeta_{sn} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align}$$
The components of the dielectric tensor (G10) in coordinate basis ![]() $\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$ then follow from (G9), although we do not write these out explicitly.
$\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$ then follow from (G9), although we do not write these out explicitly.
G.1.2. Dielectric tensor in low-frequency limit,  $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ coordinate frame
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$ coordinate frame
Now, to consider the low-frequency limit ![]() $\tilde {\omega }_{s\|} \ll 1$, we Taylor expand (G17) in
$\tilde {\omega }_{s\|} \ll 1$, we Taylor expand (G17) in ![]() $\tilde {\omega }_{s\|}$. Noting that
$\tilde {\omega }_{s\|}$. Noting that ![]() $\tilde {\omega }_{s\|}$ only appears via the argument
$\tilde {\omega }_{s\|}$ only appears via the argument ![]() $\zeta _{sn} = \tilde {\omega }_{s\|} - n/|k_{\|}| \tilde {\rho }_s$, we use the differential identity
$\zeta _{sn} = \tilde {\omega }_{s\|} - n/|k_{\|}| \tilde {\rho }_s$, we use the differential identity ![]() $Z'(z) = -2[1 + z Z(z)]$ to obtain the expansions
$Z'(z) = -2[1 + z Z(z)]$ to obtain the expansions
 \begin{align} 1+ \zeta_{sn} Z\!\left(\zeta_{sn}\right) & = 1 -\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \nonumber\\ &\quad + \tilde{\omega}_{s\|} \left[\left(1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)+ \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \right] + {O}(\tilde{\omega}_{s\|}^2) , \end{align}
\begin{align} 1+ \zeta_{sn} Z\!\left(\zeta_{sn}\right) & = 1 -\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \nonumber\\ &\quad + \tilde{\omega}_{s\|} \left[\left(1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)+ \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \right] + {O}(\tilde{\omega}_{s\|}^2) , \end{align} \begin{align} \zeta_{sn} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] & ={-} \frac{n}{|k_{\|}| \tilde{\rho}_s} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] + \tilde{\omega}_{s\|} \left[1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right. \nonumber\\ & \left. \quad - \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \left(1- \frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] + {O}(\tilde{\omega}_{s\|}^2) . \end{align}
\begin{align} \zeta_{sn} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] & ={-} \frac{n}{|k_{\|}| \tilde{\rho}_s} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] + \tilde{\omega}_{s\|} \left[1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right. \nonumber\\ & \left. \quad - \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \left(1- \frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] + {O}(\tilde{\omega}_{s\|}^2) . \end{align}Then, expanding the dielectric tensor as
we have
 \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} &= 2 \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} &= 2 \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xy} & = \mathrm{i} \sum_{n={-}\infty}^{\infty} n Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xy} & = \mathrm{i} \sum_{n={-}\infty}^{\infty} n Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xz} & = 2 \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \left[1 -\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xz} & = 2 \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \left[1 -\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{yy} & = \sum_{n={-}\infty}^{\infty} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{yy} & = \sum_{n={-}\infty}^{\infty} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{yz} & = \mathrm{i} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \left[1 -\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{yz} & = \mathrm{i} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \left[1 -\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{zz} & ={-}2 \sum_{n={-}\infty}^{\infty} \frac{n}{|k_{\|}| \tilde{\rho}_s} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}|\tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{zz} & ={-}2 \sum_{n={-}\infty}^{\infty} \frac{n}{|k_{\|}| \tilde{\rho}_s} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}|\tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}and
 \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} & ={-}4 \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} & ={-}4 \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xy} & ={-}2\mathrm{i} \sum_{n={-}\infty}^{\infty} n \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right], \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xy} & ={-}2\mathrm{i} \sum_{n={-}\infty}^{\infty} n \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right], \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} & = 2 \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \left[\left(1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) + \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} & = 2 \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \left[\left(1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) + \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yy} & ={-}2 \sum_{n={-}\infty}^{\infty} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad\times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yy} & ={-}2 \sum_{n={-}\infty}^{\infty} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad\times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yz} & ={-}\mathrm{i} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s\left[\left(1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) + \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yz} & ={-}\mathrm{i} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s\left[\left(1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) + \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{zz} & = 2 \sum_{n={-}\infty}^{\infty} \left[1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \left(1- \frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{zz} & = 2 \sum_{n={-}\infty}^{\infty} \left[1- \frac{2 n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - \frac{2 n}{|k_{\|}| \tilde{\rho}_s} \left(1- \frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right)Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align} These expressions can be simplified somewhat using two further types of algebraic manipulation. First, for ![]() $z$ a real number, we can split the plasma dispersion into real and imaginary parts as
$z$ a real number, we can split the plasma dispersion into real and imaginary parts as
 \begin{align} Z\!\left(z\right) & = \frac{1}{\sqrt{\rm \pi}} \mathcal{P} \int_{-\infty}^{\infty} \frac{\exp{\left({-}u^2\right)} \,\mathrm{d}u}{u-z} + \mathrm{i} \sqrt{\rm \pi} \exp{\left({-}z^2\right)} \nonumber\\ & = {\rm Re}{\,Z\!\left(z\right)} + \mathrm{i} \sqrt{\rm \pi} \exp{\left({-}z^2\right)} . \end{align}
\begin{align} Z\!\left(z\right) & = \frac{1}{\sqrt{\rm \pi}} \mathcal{P} \int_{-\infty}^{\infty} \frac{\exp{\left({-}u^2\right)} \,\mathrm{d}u}{u-z} + \mathrm{i} \sqrt{\rm \pi} \exp{\left({-}z^2\right)} \nonumber\\ & = {\rm Re}{\,Z\!\left(z\right)} + \mathrm{i} \sqrt{\rm \pi} \exp{\left({-}z^2\right)} . \end{align}
Thus, we see that the real part of ![]() $Z(z)$ is an odd function for real
$Z(z)$ is an odd function for real ![]() $z$, while the imaginary part is an even function. As a consequence, only one of the real or imaginary parts of the plasma dispersion function will enter into the summations in (G20) and (G21). Secondly, we utilise the generating function of the modified Bessel function, viz.
$z$, while the imaginary part is an even function. As a consequence, only one of the real or imaginary parts of the plasma dispersion function will enter into the summations in (G20) and (G21). Secondly, we utilise the generating function of the modified Bessel function, viz.
 \begin{equation} \sum_{n ={-}\infty}^{\infty} {I}_n\!\left(\alpha\right) t^{n} = \exp{\left[\frac{\alpha}{2}\left(t+\frac{1}{t}\right)\right]} , \end{equation}
\begin{equation} \sum_{n ={-}\infty}^{\infty} {I}_n\!\left(\alpha\right) t^{n} = \exp{\left[\frac{\alpha}{2}\left(t+\frac{1}{t}\right)\right]} , \end{equation}to deduce the following identities:
 $$\begin{gather} \sum_{n ={-}\infty}^{\infty} {I}_n\!\left(\alpha\right) = \exp{\left(\alpha\right)} , \end{gather}$$
$$\begin{gather} \sum_{n ={-}\infty}^{\infty} {I}_n\!\left(\alpha\right) = \exp{\left(\alpha\right)} , \end{gather}$$ $$\begin{gather}\sum_{n ={-}\infty}^{\infty} n^2 {I}_n\!\left(\alpha\right) = \alpha \exp{\left(\alpha\right)} , \end{gather}$$
$$\begin{gather}\sum_{n ={-}\infty}^{\infty} n^2 {I}_n\!\left(\alpha\right) = \alpha \exp{\left(\alpha\right)} , \end{gather}$$ $$\begin{gather}\sum_{n ={-}\infty}^{\infty} \left[ {I}_n'\!\left(\alpha\right) - {I}_n\!\left(\alpha\right) \right] = 0 , \end{gather}$$
$$\begin{gather}\sum_{n ={-}\infty}^{\infty} \left[ {I}_n'\!\left(\alpha\right) - {I}_n\!\left(\alpha\right) \right] = 0 , \end{gather}$$ $$\begin{gather}\sum_{n ={-}\infty}^{\infty} n^2 \left[{I}_n'\!\left(\alpha\right)- {I}_n\!\left(\alpha\right)\right] = \exp{\left(\alpha\right)} . \end{gather}$$
$$\begin{gather}\sum_{n ={-}\infty}^{\infty} n^2 \left[{I}_n'\!\left(\alpha\right)- {I}_n\!\left(\alpha\right)\right] = \exp{\left(\alpha\right)} . \end{gather}$$
Combining these results, we obtain from (G20) and (G21) the following expressions for the components of ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ and
$\boldsymbol{\mathsf{M}}_s^{(0)}$ and ![]() $\boldsymbol{\mathsf{M}}_s^{(1)}$:
$\boldsymbol{\mathsf{M}}_s^{(1)}$:
 \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} & = 4 \mathrm{i} \sqrt{\rm \pi} \sum_{m=1}^{\infty} \frac{m^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & = \mathrm{i} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} & = 4 \mathrm{i} \sqrt{\rm \pi} \sum_{m=1}^{\infty} \frac{m^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & = \mathrm{i} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xy} & ={-}\mathrm{i} \sum_{m={-}\infty}^{\infty} m \, {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\mathrm{i} G\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xy} & ={-}\mathrm{i} \sum_{m={-}\infty}^{\infty} m \, {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\mathrm{i} G\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xz} & ={-}4 \mathrm{i} \sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} \frac{m^2}{k_{\bot} |k_{\|}| \tilde{\rho}_s^2} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & ={-}\frac{\mathrm{i} k_{\bot}}{|k_{\|}|} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xz} & ={-}4 \mathrm{i} \sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} \frac{m^2}{k_{\bot} |k_{\|}| \tilde{\rho}_s^2} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & ={-}\frac{\mathrm{i} k_{\bot}}{|k_{\|}|} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{yy} & = \mathrm{i} \sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ &\quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2m^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & = \mathrm{i}H\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{yy} & = \mathrm{i} \sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ &\quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2m^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & = \mathrm{i}H\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{yz} & ={-}\mathrm{i} \sum_{m={-}\infty}^{\infty} \frac{m k_{\bot}}{|k_{\|}|} \, {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\frac{\mathrm{i} k_{\bot}}{|k_{\|}|} G\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{yz} & ={-}\mathrm{i} \sum_{m={-}\infty}^{\infty} \frac{m k_{\bot}}{|k_{\|}|} \, {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\frac{\mathrm{i} k_{\bot}}{|k_{\|}|} G\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{zz} & = 4 \mathrm{i} \sqrt{\rm \pi} \sum_{m=1}^{\infty} \frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & = \frac{\mathrm{i} k_{\bot}^2 }{k_{\|}^2} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{zz} & = 4 \mathrm{i} \sqrt{\rm \pi} \sum_{m=1}^{\infty} \frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & = \frac{\mathrm{i} k_{\bot}^2 }{k_{\|}^2} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}and
 \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} & ={-}2 \left\{1 + \sum_{m={-}\infty}^{\infty} \frac{2m^3}{|k_{\|}| k_{\bot}^2 \tilde{\rho}_s^3} {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]}\exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\vphantom{\sum_{m={-}\infty}^{\infty}} \right\} \nonumber\\ &={-}\frac{4}{3} W\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} & ={-}2 \left\{1 + \sum_{m={-}\infty}^{\infty} \frac{2m^3}{|k_{\|}| k_{\bot}^2 \tilde{\rho}_s^3} {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]}\exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\vphantom{\sum_{m={-}\infty}^{\infty}} \right\} \nonumber\\ &={-}\frac{4}{3} W\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xy} & = 4 \sqrt{\rm \pi} \sum_{m=1}^{\infty} \frac{m^2}{|k_{\|}| \tilde{\rho}_s} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xy} & = 4 \sqrt{\rm \pi} \sum_{m=1}^{\infty} \frac{m^2}{|k_{\|}| \tilde{\rho}_s} \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} & = 2 \left\{\frac{k_{\bot}}{|k_{\|}|} + \sum_{m={-}\infty}^{\infty} \left(\frac{2m^3}{|k_{\|}|^2 k_{\bot} \tilde{\rho}_s^3} -\frac{m}{k_{\bot} \tilde{\rho}_s}\right){\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \right. \nonumber\\ & \left. \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\vphantom{\sum_{m={-}\infty}^{\infty}} \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} & = 2 \left\{\frac{k_{\bot}}{|k_{\|}|} + \sum_{m={-}\infty}^{\infty} \left(\frac{2m^3}{|k_{\|}|^2 k_{\bot} \tilde{\rho}_s^3} -\frac{m}{k_{\bot} \tilde{\rho}_s}\right){\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \right. \nonumber\\ & \left. \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\vphantom{\sum_{m={-}\infty}^{\infty}} \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yy} & ={-}2 \left\{ 1 + \sum_{m={-}\infty}^{\infty} \frac{m}{|k_{\|}| \tilde{\rho}_s} {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \right. \nonumber\\ &\quad \times \left. \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2m^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \vphantom{\sum_{m={-}\infty}^{\infty}}\right\} \nonumber\\ &={-}\frac{4}{3} Y\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yy} & ={-}2 \left\{ 1 + \sum_{m={-}\infty}^{\infty} \frac{m}{|k_{\|}| \tilde{\rho}_s} {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \right. \nonumber\\ &\quad \times \left. \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2m^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \vphantom{\sum_{m={-}\infty}^{\infty}}\right\} \nonumber\\ &={-}\frac{4}{3} Y\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yz} & ={-}\sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \left(1-\frac{2m^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right) \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yz} & ={-}\sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \left(1-\frac{2m^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right) \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{zz} & = 2 \left\{1 - \frac{k_{\bot}^2}{k_{\|}^2} + \sum_{m={-}\infty}^{\infty} \frac{2m}{|k_{\|}| \tilde{\rho}_s} \left(1- \frac{m^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right){\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \right. \nonumber\\ & \left. \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \vphantom{\sum_{m={-}\infty}^{\infty}}\right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{zz} & = 2 \left\{1 - \frac{k_{\bot}^2}{k_{\|}^2} + \sum_{m={-}\infty}^{\infty} \frac{2m}{|k_{\|}| \tilde{\rho}_s} \left(1- \frac{m^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right){\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \right. \nonumber\\ & \left. \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \vphantom{\sum_{m={-}\infty}^{\infty}}\right\} , \end{align}
where we have reintroduced the special functions ![]() $F(x,y)$,
$F(x,y)$, ![]() $G(x,y)$ and
$G(x,y)$ and ![]() $H(x,y)$ defined by (2.122), as well as
$H(x,y)$ defined by (2.122), as well as ![]() $W(x,y)$ and
$W(x,y)$ and ![]() ${Y}(x,y)$ defined by (G97). As anticipated from the arguments presented in Appendix F,
${Y}(x,y)$ defined by (G97). As anticipated from the arguments presented in Appendix F, ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ obeys the symmetries
$\boldsymbol{\mathsf{M}}_s^{(0)}$ obeys the symmetries
 $$\begin{gather}(\boldsymbol{\mathsf{M}}_s^{(0)})_{zz} = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} . \end{gather}$$
$$\begin{gather}(\boldsymbol{\mathsf{M}}_s^{(0)})_{zz} = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} . \end{gather}$$G.1.3. Dielectric tensor in low-frequency limit,  $\{{e}_1,{e}_2,{e}_3\}$ coordinate frame
$\{{e}_1,{e}_2,{e}_3\}$ coordinate frame
Having evaluated the first- and second-order terms in the expansion for components of the dielectric tensor in the coordinate basis ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$, we can use (G9) to find equivalent expressions in the coordinate basis
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$, we can use (G9) to find equivalent expressions in the coordinate basis ![]() $\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$. Explicitly, we have the following transformations for
$\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$. Explicitly, we have the following transformations for ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$:
$\boldsymbol{\mathsf{M}}_s^{(0)}$:
 $$\begin{align}(\boldsymbol{\mathsf{M}}_s^{(0)})_{13} &= \frac{k_{\|} k_{\bot}}{k^2} \left[(\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} - (\boldsymbol{\mathsf{M}}_s^{(0)})_{zz}\right] + \left(\frac{k_{\|}^2}{k^2}- \frac{k_{\bot}^2}{k^2}\right) (\boldsymbol{\mathsf{M}}_s^{(0)})_{xz} , \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s^{(0)})_{13} &= \frac{k_{\|} k_{\bot}}{k^2} \left[(\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} - (\boldsymbol{\mathsf{M}}_s^{(0)})_{zz}\right] + \left(\frac{k_{\|}^2}{k^2}- \frac{k_{\bot}^2}{k^2}\right) (\boldsymbol{\mathsf{M}}_s^{(0)})_{xz} , \end{align}$$
and similarly for ![]() $\boldsymbol{\mathsf{M}}_s^{(1)}$.
$\boldsymbol{\mathsf{M}}_s^{(1)}$.
On account of the symmetries derived in Appendix G.1.2, we find for ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ that
$\boldsymbol{\mathsf{M}}_s^{(0)}$ that
 $$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{11} &= \frac{k^2}{k_{\|}^2}(\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{11} &= \frac{k^2}{k_{\|}^2}(\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} , \end{align}$$with all other components vanishing. This agrees with (2.104) stated in the main text. On substitution of identities (G25), (2.121) are recovered.
As for ![]() $\boldsymbol{\mathsf{M}}_s^{(1)}$, from the results (G26) derived in Appendix G.1.2, we have the following identities:
$\boldsymbol{\mathsf{M}}_s^{(1)}$, from the results (G26) derived in Appendix G.1.2, we have the following identities:
 \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} + \frac{k_{\bot}}{k_{\|}} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} & ={-}2 \sum_{m={-}\infty}^{\infty} \frac{m}{k_{\bot} \tilde{\rho}_s} {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} + \frac{k_{\bot}}{k_{\|}} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} & ={-}2 \sum_{m={-}\infty}^{\infty} \frac{m}{k_{\bot} \tilde{\rho}_s} {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yz} - \frac{k_{\bot}}{k_{\|}} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xy} & ={-}\sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{yz} - \frac{k_{\bot}}{k_{\|}} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xy} & ={-}\sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{zz} + \frac{k_{\bot}}{k_{\|}} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} & = 2 \left\{1 + \sum_{m={-}\infty}^{\infty} \frac{m}{|k_{\|}| \tilde{\rho}_s} {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \right. \nonumber\\ & \left. \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \vphantom{\sum_{m={-}\infty}^{\infty}}\right\} . \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{zz} + \frac{k_{\bot}}{k_{\|}} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} & = 2 \left\{1 + \sum_{m={-}\infty}^{\infty} \frac{m}{|k_{\|}| \tilde{\rho}_s} {\rm Re}{\left[Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \right. \nonumber\\ & \left. \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \vphantom{\sum_{m={-}\infty}^{\infty}}\right\} . \end{align}
Thus, we can decompose the dielectric components ![]() $(\boldsymbol{\mathsf{M}}_s^{(1)})_{xz}$,
$(\boldsymbol{\mathsf{M}}_s^{(1)})_{xz}$, ![]() $(\boldsymbol{\mathsf{M}}_s^{(1)})_{yz}$ and
$(\boldsymbol{\mathsf{M}}_s^{(1)})_{yz}$ and ![]() $(\boldsymbol{\mathsf{M}}_s^{(1)})_{zz}$ in terms of the remaining components of
$(\boldsymbol{\mathsf{M}}_s^{(1)})_{zz}$ in terms of the remaining components of ![]() $\boldsymbol{\mathsf{M}}_s^{(1)}$ as follows:
$\boldsymbol{\mathsf{M}}_s^{(1)}$ as follows:
 $$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{zz} & ={-}\frac{k_{\bot}}{k_{\|}} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} + \left[2 + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] \nonumber\\ & = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} + 2\left[1 + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{zz} & ={-}\frac{k_{\bot}}{k_{\|}} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xz} + \left[2 + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] \nonumber\\ & = \frac{k_{\bot}^2}{k_{\|}^2} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} + 2\left[1 + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] , \end{align}$$
where the special functions ![]() $L(x,y)$ and
$L(x,y)$ and ![]() $N(x,y)$ are defined by
$N(x,y)$ are defined by
 $$\begin{align} L\!\left(x,y\right) &\equiv \sum_{m={-}\infty}^{\infty} \frac{2m}{y} {\rm Re}{\,Z\!\left(\frac{m}{x}\right)} \exp \left(-\frac{y^2}{2}\right) {I}_m\!\left(\frac{y^2}{2}\right) , \end{align}$$
$$\begin{align} L\!\left(x,y\right) &\equiv \sum_{m={-}\infty}^{\infty} \frac{2m}{y} {\rm Re}{\,Z\!\left(\frac{m}{x}\right)} \exp \left(-\frac{y^2}{2}\right) {I}_m\!\left(\frac{y^2}{2}\right) , \end{align}$$ $$\begin{align}N\!\left(x,y\right) &\equiv \sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} y \exp{\left(-\frac{m^2}{x^2}\right)} \exp \left(-\frac{y^2}{2}\right) \left[{I}_m'\!\left(\frac{y^2}{2}\right)-{I}_m\!\left(\frac{y^2}{2}\right) \right] . \end{align}$$
$$\begin{align}N\!\left(x,y\right) &\equiv \sqrt{\rm \pi} \sum_{m={-}\infty}^{\infty} y \exp{\left(-\frac{m^2}{x^2}\right)} \exp \left(-\frac{y^2}{2}\right) \left[{I}_m'\!\left(\frac{y^2}{2}\right)-{I}_m\!\left(\frac{y^2}{2}\right) \right] . \end{align}$$This leads to the following expressions:
 $$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{11} &= \frac{k^2} {k_{\|}^2} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} + 2 \left[\frac{k_{\bot}^2}{k^2} + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(1)})_{11} &= \frac{k^2} {k_{\|}^2} (\boldsymbol{\mathsf{M}}_s^{(1)})_{xx} + 2 \left[\frac{k_{\bot}^2}{k^2} + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] , \end{align}$$
We note that ![]() $\boldsymbol{\mathsf{M}}_s^{(1)}$ does not possess the same symmetry properties as
$\boldsymbol{\mathsf{M}}_s^{(1)}$ does not possess the same symmetry properties as ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$.
$\boldsymbol{\mathsf{M}}_s^{(0)}$.
G.1.4. Asymptotic forms of  $\boldsymbol{\mathsf{M}}_s^{(0)}$ and
$\boldsymbol{\mathsf{M}}_s^{(0)}$ and  $\boldsymbol{\mathsf{M}}_s^{(1)}$
$\boldsymbol{\mathsf{M}}_s^{(1)}$
In this appendix, we write down asymptotic forms at small and large ![]() $x$ and
$x$ and ![]() $y$ for the special functions
$y$ for the special functions ![]() $F(x,y)$,
$F(x,y)$, ![]() $G(x,y)$,
$G(x,y)$, ![]() $H(x,y)$,
$H(x,y)$, ![]() $L(x,y)$ and
$L(x,y)$ and ![]() $N(x,y)$ defined by (2.122) and (G32), respectively. Physically, this corresponds via (2.121) to considering the dielectric response associated with
$N(x,y)$ defined by (2.122) and (G32), respectively. Physically, this corresponds via (2.121) to considering the dielectric response associated with ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ and
$\boldsymbol{\mathsf{M}}_s^{(0)}$ and ![]() $\boldsymbol{\mathsf{M}}_s^{(1)}$ for modes with parallel and perpendicular wavenumbers very small (or very large) with respect to the inverse Larmor radius of species
$\boldsymbol{\mathsf{M}}_s^{(1)}$ for modes with parallel and perpendicular wavenumbers very small (or very large) with respect to the inverse Larmor radius of species ![]() $s$. Detailed derivations are left as an exercise to keen readers (and can be verified numerically).
$s$. Detailed derivations are left as an exercise to keen readers (and can be verified numerically).
Proceeding systematically through various limits, we have the following results:
(i)
 $x \sim 1$,
$x \sim 1$,  $y \ll 1$
(G34a)
$y \ll 1$
(G34a) $$\begin{align} F\!\left(x,y\right) &= \sqrt{\rm \pi} \exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G34b)
$$\begin{align} F\!\left(x,y\right) &= \sqrt{\rm \pi} \exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G34b) $$\begin{align}G\!\left(x,y\right) &= {\rm Re}{\left[Z\left(\frac{1}{x}\right)\right]} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G34c)
$$\begin{align}G\!\left(x,y\right) &= {\rm Re}{\left[Z\left(\frac{1}{x}\right)\right]} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G34c) $$\begin{align}H\!\left(x,y\right) &= \sqrt{\rm \pi} \exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G34d)
$$\begin{align}H\!\left(x,y\right) &= \sqrt{\rm \pi} \exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G34d) $$\begin{align}L\!\left(x,y\right) &= y \,{\rm Re}{\left[Z\left(\frac{1}{x}\right)\right]} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G34e)
$$\begin{align}L\!\left(x,y\right) &= y \,{\rm Re}{\left[Z\left(\frac{1}{x}\right)\right]} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G34e) $$\begin{align}N\!\left(x,y\right) &= \sqrt{\rm \pi} y \left[2 \exp{\left(-\frac{1}{x^2}\right)} - 1 \right] \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] . \end{align}$$
$$\begin{align}N\!\left(x,y\right) &= \sqrt{\rm \pi} y \left[2 \exp{\left(-\frac{1}{x^2}\right)} - 1 \right] \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] . \end{align}$$(ii)
 $x, y \gg 1$
(G35a)
$x, y \gg 1$
(G35a) $$\begin{align} F\!\left(x,y\right) &= \frac{\sqrt{\rm \pi} x^3}{\left(x^2+y^2\right)^{3/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G35b)
$$\begin{align} F\!\left(x,y\right) &= \frac{\sqrt{\rm \pi} x^3}{\left(x^2+y^2\right)^{3/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G35b) $$\begin{align}G\!\left(x,y\right) &={-}\frac{2 x^3}{\left(x^2+y^2\right)^{2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G35c)
$$\begin{align}G\!\left(x,y\right) &={-}\frac{2 x^3}{\left(x^2+y^2\right)^{2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G35c) $$\begin{align}H\!\left(x,y\right) &= \frac{\sqrt{\rm \pi} x}{\left(x^2+y^2\right)^{1/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G35d)
$$\begin{align}H\!\left(x,y\right) &= \frac{\sqrt{\rm \pi} x}{\left(x^2+y^2\right)^{1/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G35d) $$\begin{align}L\!\left(x,y\right) &={-}\frac{2 x y}{x^2+y^2} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G35e)We observe that the asymptotic forms (G35) are in fact valid even for
$$\begin{align}L\!\left(x,y\right) &={-}\frac{2 x y}{x^2+y^2} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G35e)We observe that the asymptotic forms (G35) are in fact valid even for $$\begin{align}N\!\left(x,y\right) &= \frac{\sqrt{\rm \pi} x}{y \left(x^2+y^2\right)^{1/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] . \end{align}$$
$$\begin{align}N\!\left(x,y\right) &= \frac{\sqrt{\rm \pi} x}{y \left(x^2+y^2\right)^{1/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] . \end{align}$$ $y \lesssim 1$.
$y \lesssim 1$.(iii)
 $x \ll 1$,
$x \ll 1$,  $y \sim 1$
(G36a)
$y \sim 1$
(G36a) $$\begin{align} F\!\left(x,y\right) &= \frac{4 \sqrt{\rm \pi}}{y^2} \exp{\left(-\frac{y^2}{2}\right)} {I}_1\!\left(\frac{y^2}{2}\right)\exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)} \right] \right\} , \end{align}$$(G36b)
$$\begin{align} F\!\left(x,y\right) &= \frac{4 \sqrt{\rm \pi}}{y^2} \exp{\left(-\frac{y^2}{2}\right)} {I}_1\!\left(\frac{y^2}{2}\right)\exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)} \right] \right\} , \end{align}$$(G36b) $$\begin{align}G\!\left(x,y\right) &={-}x \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)- {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}$$(G36c)
$$\begin{align}G\!\left(x,y\right) &={-}x \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)- {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}$$(G36c) $$\begin{align}H\!\left(x,y\right) &= \sqrt{\rm \pi} y^2 \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)- {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}$$(G36d)
$$\begin{align}H\!\left(x,y\right) &= \sqrt{\rm \pi} y^2 \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)- {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}$$(G36d) $$\begin{align}L\!\left(x,y\right) &={-}\frac{2 x}{y} \left[1-\exp \left(-\frac{y^2}{2}\right) {I}_0\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}$$(G36e)
$$\begin{align}L\!\left(x,y\right) &={-}\frac{2 x}{y} \left[1-\exp \left(-\frac{y^2}{2}\right) {I}_0\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}$$(G36e) $$\begin{align}N\!\left(x,y\right) &={-}\sqrt{\rm \pi} y \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)- {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] . \end{align}$$
$$\begin{align}N\!\left(x,y\right) &={-}\sqrt{\rm \pi} y \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)- {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] . \end{align}$$(iv)
 $x, y \ll 1$
(G37a)
$x, y \ll 1$
(G37a) \begin{align} F\!\left(x,y\right) &= \sqrt{\rm \pi} \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)},y^2 \right] \right\} , \end{align}(G37b)
\begin{align} F\!\left(x,y\right) &= \sqrt{\rm \pi} \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)},y^2 \right] \right\} , \end{align}(G37b) \begin{align} G\!\left(x,y\right) & ={-}x \left[1 - \left(\frac{3}{4}y^2 - \frac{1}{2} x^2\right) \right. \nonumber\\ & \left. \quad + \left(\frac{3}{4} x^4-\frac{15}{32} x^2 y^2 + \frac{5}{16}y^4\right) \right] \left[1+{O}\!\left(x^6, x^4 y^2, x^2 y^4, y^6\right) \right] , \end{align}(G37c)
\begin{align} G\!\left(x,y\right) & ={-}x \left[1 - \left(\frac{3}{4}y^2 - \frac{1}{2} x^2\right) \right. \nonumber\\ & \left. \quad + \left(\frac{3}{4} x^4-\frac{15}{32} x^2 y^2 + \frac{5}{16}y^4\right) \right] \left[1+{O}\!\left(x^6, x^4 y^2, x^2 y^4, y^6\right) \right] , \end{align}(G37c) \begin{align} H\!\left(x,y\right) & = \sqrt{\rm \pi} y^2 \left[ 1 - \left(\frac{3}{4}y^2 - \frac{1}{2} x^2\right) \right. \nonumber\\ & \left. \quad + \left(\frac{3}{4} x^4-\frac{15}{32} x^2 y^2 + \frac{5}{16}y^4\right) \right] \left[1+{O}\!\left(x^6, x^4 y^2, x^2 y^4, y^6\right) \right] , \end{align}(G37d)
\begin{align} H\!\left(x,y\right) & = \sqrt{\rm \pi} y^2 \left[ 1 - \left(\frac{3}{4}y^2 - \frac{1}{2} x^2\right) \right. \nonumber\\ & \left. \quad + \left(\frac{3}{4} x^4-\frac{15}{32} x^2 y^2 + \frac{5}{16}y^4\right) \right] \left[1+{O}\!\left(x^6, x^4 y^2, x^2 y^4, y^6\right) \right] , \end{align}(G37d) \begin{align} L\!\left(x,y\right) &={-}x y \left[1+{O}\!\left(x^2, y^2\right) \right] , \end{align}(G37e)
\begin{align} L\!\left(x,y\right) &={-}x y \left[1+{O}\!\left(x^2, y^2\right) \right] , \end{align}(G37e) \begin{align} N\!\left(x,y\right) &={-}\sqrt{\rm \pi} y \left[1+{O}\!\left(x^2\right) \right] \left[1+{O}\!\left(x^2, y^2\right) \right] . \end{align}
\begin{align} N\!\left(x,y\right) &={-}\sqrt{\rm \pi} y \left[1+{O}\!\left(x^2\right) \right] \left[1+{O}\!\left(x^2, y^2\right) \right] . \end{align}(v)
 $x \ll 1$,
$x \ll 1$,  $y \gg 1$
(G38a)
$y \gg 1$
(G38a) $$\begin{align} F\!\left(x,y\right) &= \frac{4}{y^3} \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)}, \frac{1}{y^2} \right] \right\} , \end{align}$$(G38b)
$$\begin{align} F\!\left(x,y\right) &= \frac{4}{y^3} \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)}, \frac{1}{y^2} \right] \right\} , \end{align}$$(G38b) $$\begin{align}G\!\left(x,y\right) &={-}\frac{x}{\sqrt{\rm \pi} y^3} \left[1+{O}\!\left(\frac{1}{y^2}\right) \right] , \end{align}$$(G38c)
$$\begin{align}G\!\left(x,y\right) &={-}\frac{x}{\sqrt{\rm \pi} y^3} \left[1+{O}\!\left(\frac{1}{y^2}\right) \right] , \end{align}$$(G38c) $$\begin{align}H\!\left(x,y\right) &= \frac{1}{y} \left[1+{O}\!\left(\frac{1}{y^2}\right) \right] , \end{align}$$(G38d)
$$\begin{align}H\!\left(x,y\right) &= \frac{1}{y} \left[1+{O}\!\left(\frac{1}{y^2}\right) \right] , \end{align}$$(G38d) $$\begin{align}L\!\left(x,y\right) &={-}\frac{2 x}{y} \left[1-\frac{1}{\sqrt{\rm \pi} y}\right]\left[1+{O}\!\left(x^2,\frac{1}{y^3}\right) \right] , \end{align}$$(G38e)
$$\begin{align}L\!\left(x,y\right) &={-}\frac{2 x}{y} \left[1-\frac{1}{\sqrt{\rm \pi} y}\right]\left[1+{O}\!\left(x^2,\frac{1}{y^3}\right) \right] , \end{align}$$(G38e) $$\begin{align}N\!\left(x,y\right) &={-}\frac{1}{y^2} \left[1+{O}\!\left(\frac{1}{y^2}\right) \right] . \end{align}$$
$$\begin{align}N\!\left(x,y\right) &={-}\frac{1}{y^2} \left[1+{O}\!\left(\frac{1}{y^2}\right) \right] . \end{align}$$
G.1.5. Unmagnetised Maxwellian dielectric response
In this paper, we consider microinstabilities over a wide range of scales, from ![]() $k \rho _i \ll 1$ to sub-electron-scale microinstabilities with
$k \rho _i \ll 1$ to sub-electron-scale microinstabilities with ![]() $k \rho _e \gg 1$. Therefore, the ordering
$k \rho _e \gg 1$. Therefore, the ordering ![]() $k \rho _s \sim 1$ assumed in § 2.5.3 for the derivation of the low-frequency dielectric tensor in a magnetised plasma cannot hold for both ions and electrons (as was noted in § 2.5.5 and discussed in § 2.5.6). While the derivation of the dielectric tensor in a strongly magnetised plasma (
$k \rho _s \sim 1$ assumed in § 2.5.3 for the derivation of the low-frequency dielectric tensor in a magnetised plasma cannot hold for both ions and electrons (as was noted in § 2.5.5 and discussed in § 2.5.6). While the derivation of the dielectric tensor in a strongly magnetised plasma (![]() $k \rho _s \ll 1$) is straightforwardly performed by asymptotic analysis applied directly to the hot, magnetised plasma conductivity tensor (2.77), the equivalent calculation for
$k \rho _s \ll 1$) is straightforwardly performed by asymptotic analysis applied directly to the hot, magnetised plasma conductivity tensor (2.77), the equivalent calculation for ![]() $k \rho _s \gg 1$ is most easily done by direct analysis of the Vlasov equation with
$k \rho _s \gg 1$ is most easily done by direct analysis of the Vlasov equation with ![]() $\boldsymbol {B}_0 = 0$. In this appendix, we present such a calculation.
$\boldsymbol {B}_0 = 0$. In this appendix, we present such a calculation.
We begin from (C8), but with ![]() $\tilde {\varOmega }_s = 0$ (and ignoring the displacement current):
$\tilde {\varOmega }_s = 0$ (and ignoring the displacement current):
As with the magnetised case, we substitute the perturbed distribution function (G39c) into the current (G39b):
 \begin{equation} \widehat{\delta \boldsymbol{j}} ={-}\mathrm{i} \sum_s \frac{Z_s^2 e^2}{m_s} \int \mathrm{d}^3 \boldsymbol{v} \, \frac{\boldsymbol{v} }{\omega - \boldsymbol{k} \boldsymbol{\cdot} \boldsymbol{v}} \left[\widehat{\delta \boldsymbol{E}} + \frac{k}{\omega} \boldsymbol{v} \times \left(\hat{\boldsymbol{k}} \times \widehat{\delta \boldsymbol{E}}\right)\right] \boldsymbol{\cdot} \frac{\partial f_{s0}}{\partial \boldsymbol{v}} . \end{equation}
\begin{equation} \widehat{\delta \boldsymbol{j}} ={-}\mathrm{i} \sum_s \frac{Z_s^2 e^2}{m_s} \int \mathrm{d}^3 \boldsymbol{v} \, \frac{\boldsymbol{v} }{\omega - \boldsymbol{k} \boldsymbol{\cdot} \boldsymbol{v}} \left[\widehat{\delta \boldsymbol{E}} + \frac{k}{\omega} \boldsymbol{v} \times \left(\hat{\boldsymbol{k}} \times \widehat{\delta \boldsymbol{E}}\right)\right] \boldsymbol{\cdot} \frac{\partial f_{s0}}{\partial \boldsymbol{v}} . \end{equation}Non-dimensionalising the distribution function via
we obtain
 \begin{equation} \widehat{\delta \boldsymbol{j}} ={-}\frac{\mathrm{i}}{4 {\rm \pi}\omega} \sum_s \omega_{{\rm p}s}^2 \frac{\tilde{\omega}_s}{{\rm \pi}^{3/2}} \int \mathrm{d}^3 \widetilde{\boldsymbol{v}_s} \, \frac{ \widetilde{\boldsymbol{v}_s}}{\tilde{\omega}_s - \widehat{ \boldsymbol{k}} \boldsymbol{\cdot} \tilde{\boldsymbol{v}}_s} \left[\widehat{\delta \boldsymbol{E}} + \frac{1}{\tilde{\omega}_s} \tilde{\boldsymbol{v}}_s \times \left(\hat{\boldsymbol{k}} \times \widehat{\delta \boldsymbol{E}}\right)\right] \boldsymbol{\cdot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{\boldsymbol{v}}_s} , \end{equation}
\begin{equation} \widehat{\delta \boldsymbol{j}} ={-}\frac{\mathrm{i}}{4 {\rm \pi}\omega} \sum_s \omega_{{\rm p}s}^2 \frac{\tilde{\omega}_s}{{\rm \pi}^{3/2}} \int \mathrm{d}^3 \widetilde{\boldsymbol{v}_s} \, \frac{ \widetilde{\boldsymbol{v}_s}}{\tilde{\omega}_s - \widehat{ \boldsymbol{k}} \boldsymbol{\cdot} \tilde{\boldsymbol{v}}_s} \left[\widehat{\delta \boldsymbol{E}} + \frac{1}{\tilde{\omega}_s} \tilde{\boldsymbol{v}}_s \times \left(\hat{\boldsymbol{k}} \times \widehat{\delta \boldsymbol{E}}\right)\right] \boldsymbol{\cdot} \frac{\partial \tilde{f}_{s0}}{\partial \tilde{\boldsymbol{v}}_s} , \end{equation}
where ![]() $\tilde {\omega }_s = \omega /k v_{\mathrm {th}s}$. For a Maxwellian distribution, with
$\tilde {\omega }_s = \omega /k v_{\mathrm {th}s}$. For a Maxwellian distribution, with
the second term in (G42) vanishes, leaving
where the conductivity tensor is
The integral can be evaluated to give
The dielectric tensor in an unmagnetised Maxwellian plasma for general ![]() $\tilde {\omega }_s$ is, therefore,
$\tilde {\omega }_s$ is, therefore,
 \begin{equation} \boldsymbol{\mathfrak{E}}^{\rm (UM)} = \sum_s \frac{\omega_{{\rm p}s}^2}{\omega^2} \tilde{\omega}_s \left\{Z\!\left(\tilde{\omega}_s\right) \left(\boldsymbol{\mathsf{I}}-\hat{\boldsymbol{k}}\hat{\boldsymbol{k}}\right) + 2 \left[\tilde{\omega}_s + \tilde{\omega}_s^2 Z\!\left(\tilde{\omega}_s\right) \right]\hat{\boldsymbol{k}}\hat{\boldsymbol{k}}\right\} . \end{equation}
\begin{equation} \boldsymbol{\mathfrak{E}}^{\rm (UM)} = \sum_s \frac{\omega_{{\rm p}s}^2}{\omega^2} \tilde{\omega}_s \left\{Z\!\left(\tilde{\omega}_s\right) \left(\boldsymbol{\mathsf{I}}-\hat{\boldsymbol{k}}\hat{\boldsymbol{k}}\right) + 2 \left[\tilde{\omega}_s + \tilde{\omega}_s^2 Z\!\left(\tilde{\omega}_s\right) \right]\hat{\boldsymbol{k}}\hat{\boldsymbol{k}}\right\} . \end{equation}
Note that it follows from (G39) that ![]() $\boldsymbol {\mathfrak {E}} \boldsymbol {\cdot } \hat {\boldsymbol {k}} = 0$, so we conclude that for non-zero fluctuations, either
$\boldsymbol {\mathfrak {E}} \boldsymbol {\cdot } \hat {\boldsymbol {k}} = 0$, so we conclude that for non-zero fluctuations, either ![]() $\hat {\boldsymbol {k}} \boldsymbol {\cdot } \widehat {\delta \boldsymbol {E}} = 0$ or
$\hat {\boldsymbol {k}} \boldsymbol {\cdot } \widehat {\delta \boldsymbol {E}} = 0$ or ![]() $1 + \tilde {\omega }_s Z(\tilde {\omega }_s) = 0$. We do not find the conventional longitudinal plasma waves because we have neglected the displacement current in Maxwell's equations. The only modes that satisfy
$1 + \tilde {\omega }_s Z(\tilde {\omega }_s) = 0$. We do not find the conventional longitudinal plasma waves because we have neglected the displacement current in Maxwell's equations. The only modes that satisfy ![]() $1 + \tilde {\omega }_s Z(\tilde {\omega }_s) = 0$ are strongly damped, with
$1 + \tilde {\omega }_s Z(\tilde {\omega }_s) = 0$ are strongly damped, with ![]() $\tilde {\omega }_s \sim 1$. Thus, all modes satisfying
$\tilde {\omega }_s \sim 1$. Thus, all modes satisfying ![]() $\tilde {\omega }_s \ll 1$ must be purely transverse.
$\tilde {\omega }_s \ll 1$ must be purely transverse.
For ![]() $\tilde {\omega }_s \ll 1$, the unmagnetised dielectric response therefore simplifies to
$\tilde {\omega }_s \ll 1$, the unmagnetised dielectric response therefore simplifies to
 \begin{equation} \boldsymbol{\mathfrak{E}}^{\rm (UM)} = \mathrm{i} \sqrt{\rm \pi} \left(\boldsymbol{\mathsf{I}}-\hat{\boldsymbol{k}}\hat{\boldsymbol{k}}\right) \sum_s \frac{\omega_{{\rm p}s}^2}{\omega^2} \tilde{\omega}_s \left[1+{O}\!\left(\tilde{\omega}_s \right) \right] . \end{equation}
\begin{equation} \boldsymbol{\mathfrak{E}}^{\rm (UM)} = \mathrm{i} \sqrt{\rm \pi} \left(\boldsymbol{\mathsf{I}}-\hat{\boldsymbol{k}}\hat{\boldsymbol{k}}\right) \sum_s \frac{\omega_{{\rm p}s}^2}{\omega^2} \tilde{\omega}_s \left[1+{O}\!\left(\tilde{\omega}_s \right) \right] . \end{equation}G.1.6. Validity of approximation  $\boldsymbol{\mathsf{M}}_s \approx \boldsymbol{\mathsf{M}}_s^{(0)}$ for large or small
$\boldsymbol{\mathsf{M}}_s \approx \boldsymbol{\mathsf{M}}_s^{(0)}$ for large or small  $k_{\|} \rho _s$ and
$k_{\|} \rho _s$ and  $k_{\bot } \rho _s$
$k_{\bot } \rho _s$
In carrying out the expansion of the Maxwellian dielectric tensor (G17) in ![]() $\tilde {\omega }_{s\|}$, we assumed that
$\tilde {\omega }_{s\|}$, we assumed that ![]() $k \rho _s \sim 1$; however, in general, we will wish to consider microinstabilities that exist at typical wavenumbers
$k \rho _s \sim 1$; however, in general, we will wish to consider microinstabilities that exist at typical wavenumbers ![]() $k \rho _s \ll 1$ or
$k \rho _s \ll 1$ or ![]() $k \rho _s \gg 1$. Indeed, since the mass ratio
$k \rho _s \gg 1$. Indeed, since the mass ratio ![]() $\mu _e = m_e/m_i$ is very small, if we wish to consider the combined response of both species, it is inevitable that for one of them,
$\mu _e = m_e/m_i$ is very small, if we wish to consider the combined response of both species, it is inevitable that for one of them, ![]() $k \rho _s \ll 1$ or
$k \rho _s \ll 1$ or ![]() $k \rho _s \gg 1$. Thus, it remains to assess when the approximation
$k \rho _s \gg 1$. Thus, it remains to assess when the approximation ![]() $\boldsymbol{\mathsf{M}}_s \approx \boldsymbol{\mathsf{M}}_s^{(0)}$ is valid in these limits. We show in this appendix that this approximation is appropriate in the limit
$\boldsymbol{\mathsf{M}}_s \approx \boldsymbol{\mathsf{M}}_s^{(0)}$ is valid in these limits. We show in this appendix that this approximation is appropriate in the limit ![]() $k_{\|} \rho _s \gg 1$, for arbitrary
$k_{\|} \rho _s \gg 1$, for arbitrary ![]() $k_{\bot } \rho _s$; however, for
$k_{\bot } \rho _s$; however, for ![]() $k_{\|} \rho _s \ll 1$, the approximation breaks down for some dielectric components – indeed, in the limit
$k_{\|} \rho _s \ll 1$, the approximation breaks down for some dielectric components – indeed, in the limit ![]() $k_\| \rho _s, k_\bot \rho _s \ll 1$, it breaks down for all but two components. For these instances, an alternative expression for the dielectric tensor is derived below.
$k_\| \rho _s, k_\bot \rho _s \ll 1$, it breaks down for all but two components. For these instances, an alternative expression for the dielectric tensor is derived below.
The validity of the ![]() $k_{\|} \rho _s \gg 1$ limit is most simply demonstrated by comparing the components of
$k_{\|} \rho _s \gg 1$ limit is most simply demonstrated by comparing the components of ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ with the unmagnetised dielectric response (G48). Recalling that
$\boldsymbol{\mathsf{M}}_s^{(0)}$ with the unmagnetised dielectric response (G48). Recalling that
 $$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{11} &= \mathrm{i} \tilde{\omega}_{s\|} \frac{k^2}{k_{\|}^2} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{11} &= \mathrm{i} \tilde{\omega}_{s\|} \frac{k^2}{k_{\|}^2} F\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}$$and applying the asymptotic results (G35), we find
We note these expressions are valid for arbitrary ![]() $k_{\bot } \rho _s$. The equivalent components of the unmagnetised (normalised) dielectric tensor
$k_{\bot } \rho _s$. The equivalent components of the unmagnetised (normalised) dielectric tensor ![]() $\boldsymbol{\mathsf{M}}_s \approx \omega ^2 \boldsymbol {\mathfrak {E}}_s^{\rm (UM)}/\omega _{{\rm p}s}^2$ are
$\boldsymbol{\mathsf{M}}_s \approx \omega ^2 \boldsymbol {\mathfrak {E}}_s^{\rm (UM)}/\omega _{{\rm p}s}^2$ are
Noting that ![]() $\tilde {\omega }_{s} = \tilde {\omega }_{s\|} k_{\|}/k$, we see that the diagonal terms are identical, while the non-zero
$\tilde {\omega }_{s} = \tilde {\omega }_{s\|} k_{\|}/k$, we see that the diagonal terms are identical, while the non-zero ![]() $\boldsymbol {e}_1 \boldsymbol {e}_2$ term present in the
$\boldsymbol {e}_1 \boldsymbol {e}_2$ term present in the ![]() $k \rho _s \gg 1$ limit of
$k \rho _s \gg 1$ limit of ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ becomes asymptotically small in
$\boldsymbol{\mathsf{M}}_s^{(0)}$ becomes asymptotically small in ![]() $1/k \rho _s \ll 1$.
$1/k \rho _s \ll 1$.
To demonstrate that the approximation ![]() $\boldsymbol{\mathsf{M}}_s \approx \boldsymbol{\mathsf{M}}_s^{(0)}$ is not accurate in the limit
$\boldsymbol{\mathsf{M}}_s \approx \boldsymbol{\mathsf{M}}_s^{(0)}$ is not accurate in the limit ![]() $k_{\|} \rho _s \ll 1$, we consider the full Maxwellian dielectric tensor assuming
$k_{\|} \rho _s \ll 1$, we consider the full Maxwellian dielectric tensor assuming ![]() $\tilde {\omega }_{s\|} \lesssim 1$ and
$\tilde {\omega }_{s\|} \lesssim 1$ and ![]() $k_{\|} \rho _s \ll 1$. If this long-wavenumber dielectric tensor subsequently evaluated at low frequencies
$k_{\|} \rho _s \ll 1$. If this long-wavenumber dielectric tensor subsequently evaluated at low frequencies ![]() $\tilde {\omega }_{s\|} \ll 1$ gives the same result as
$\tilde {\omega }_{s\|} \ll 1$ gives the same result as ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ for any particular component of
$\boldsymbol{\mathsf{M}}_s^{(0)}$ for any particular component of ![]() $\boldsymbol{\mathsf{M}}_s$, then the approximation for that component is reasonable; otherwise, the approximation has to be modified at sufficiently small
$\boldsymbol{\mathsf{M}}_s$, then the approximation for that component is reasonable; otherwise, the approximation has to be modified at sufficiently small ![]() $k_{\|} \rho _s \ll 1$.
$k_{\|} \rho _s \ll 1$.
If ![]() $k_{\|} \rho _s \ll 1$ and
$k_{\|} \rho _s \ll 1$ and ![]() $\tilde {\omega }_{s\|} \lesssim 1$, it follows that, for
$\tilde {\omega }_{s\|} \lesssim 1$, it follows that, for ![]() $n \neq 0$,
$n \neq 0$,
In this case, we can simplify the plasma dispersion function via a large-argument expansion
The long-wavelength dielectric tensor is then
 $$\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} &\approx{-}2 \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n^2}{ \zeta_{sn} k_{\bot}^2 \tilde{\rho}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} &\approx{-}2 \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n^2}{ \zeta_{sn} k_{\bot}^2 \tilde{\rho}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$ $$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xy} &\approx{-}\mathrm{i} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xy} &\approx{-}\mathrm{i} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}$$ $$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xz} &\approx{-} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n}{\zeta_{sn}^2 k_{\bot} \tilde{\rho}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xz} &\approx{-} \tilde{\omega}_{s\|} \sum_{n={-}\infty}^{\infty} \frac{n}{\zeta_{sn}^2 k_{\bot} \tilde{\rho}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$ \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} &\approx{-} \tilde{\omega}_{s\|}\left[ \sum_{n \in \mathbb{Z}^{{\neq}}} \left\{\frac{1}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right.\right. \nonumber\\ &\quad \left.\times\, \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\}\nonumber\\ &\quad \left. -\, Z\!\left(\tilde{\omega}_{s\|}\right) k_{\bot}^2 \tilde{\rho}_s^2 \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \vphantom{\sum_{n \in \mathbb{Z}^{{\neq}}} \left\{\frac{1}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}}\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} &\approx{-} \tilde{\omega}_{s\|}\left[ \sum_{n \in \mathbb{Z}^{{\neq}}} \left\{\frac{1}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right.\right. \nonumber\\ &\quad \left.\times\, \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\}\nonumber\\ &\quad \left. -\, Z\!\left(\tilde{\omega}_{s\|}\right) k_{\bot}^2 \tilde{\rho}_s^2 \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \vphantom{\sum_{n \in \mathbb{Z}^{{\neq}}} \left\{\frac{1}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}}\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} &\approx \mathrm{i} \tilde{\omega}_{s\|} \left[ \sum_{n \in \mathbb{Z}^{{\neq}}} \left\{ \frac{1}{2 \zeta_{sn}^2} k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\}\right. \nonumber\\ &\quad \left.+\, \left[1+ \tilde{\omega}_{s\|} Z\!\left(\tilde{\omega}_{s\|}\right) \right] k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}\vphantom{\sum_{n \in \mathbb{Z}^{{\neq}}} \left\{ \frac{1}{2 \zeta_{sn}^2} k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\}}\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} &\approx \mathrm{i} \tilde{\omega}_{s\|} \left[ \sum_{n \in \mathbb{Z}^{{\neq}}} \left\{ \frac{1}{2 \zeta_{sn}^2} k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\}\right. \nonumber\\ &\quad \left.+\, \left[1+ \tilde{\omega}_{s\|} Z\!\left(\tilde{\omega}_{s\|}\right) \right] k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}\vphantom{\sum_{n \in \mathbb{Z}^{{\neq}}} \left\{ \frac{1}{2 \zeta_{sn}^2} k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\}}\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{zz} &\approx{-} \tilde{\omega}_{s\|} \left[ \sum_{n \in \mathbb{Z}^{{\neq}}} \left\{ \frac{1}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right\} \right. \nonumber\\ &\quad \left.-\, 2 \tilde{\omega}_{s\|} \left[1+ \tilde{\omega}_{s\|} Z\!\left(\tilde{\omega}_{s\|}\right) \right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \vphantom{\sum_{n \in \mathbb{Z}^{{\neq}}} \left\{ \frac{1}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right\}} \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{zz} &\approx{-} \tilde{\omega}_{s\|} \left[ \sum_{n \in \mathbb{Z}^{{\neq}}} \left\{ \frac{1}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right\} \right. \nonumber\\ &\quad \left.-\, 2 \tilde{\omega}_{s\|} \left[1+ \tilde{\omega}_{s\|} Z\!\left(\tilde{\omega}_{s\|}\right) \right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \vphantom{\sum_{n \in \mathbb{Z}^{{\neq}}} \left\{ \frac{1}{\zeta_{sn}} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right\}} \right] , \end{align}
where ![]() $\mathbb {Z}^{\neq }$ denotes non-zero integers. We note that the error associated with neglecting higher-order terms in
$\mathbb {Z}^{\neq }$ denotes non-zero integers. We note that the error associated with neglecting higher-order terms in ![]() $\zeta _{sn}$ is
$\zeta _{sn}$ is ![]() ${O}(k_{\|}^2 \rho _s^2)$. Next, using
${O}(k_{\|}^2 \rho _s^2)$. Next, using
we can isolate the dependence of each dielectric tensor component on ![]() $\tilde {\omega }_{s\|}$. It is clear that any sum involving an odd power of
$\tilde {\omega }_{s\|}$. It is clear that any sum involving an odd power of ![]() $n$ vanishes, meaning that the leading-order contributions in
$n$ vanishes, meaning that the leading-order contributions in ![]() $k_{\|} \tilde {\rho }_s$ from the summation terms arise from the highest power of
$k_{\|} \tilde {\rho }_s$ from the summation terms arise from the highest power of ![]() $\tilde {\omega }_{s\|}$ gives an even power of
$\tilde {\omega }_{s\|}$ gives an even power of ![]() $n$. The resulting approximate expressions are
$n$. The resulting approximate expressions are
 $$\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} &\approx \frac{2 k_{\|}^2}{k_{\bot}^2} \tilde{\omega}_{s\|}^2 \left[1-\exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} &\approx \frac{2 k_{\|}^2}{k_{\bot}^2} \tilde{\omega}_{s\|}^2 \left[1-\exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] , \end{align}$$ $$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xz} &\approx{-}4 k_{\|}^2 \tilde{\rho}_s^2 \frac{k_{\|}}{k_{\bot}} \tilde{\omega}_{s\|}^2 \sum_{n =1}^{\infty} \frac{1}{n^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xz} &\approx{-}4 k_{\|}^2 \tilde{\rho}_s^2 \frac{k_{\|}}{k_{\bot}} \tilde{\omega}_{s\|}^2 \sum_{n =1}^{\infty} \frac{1}{n^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$ \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} &\approx \tilde{\omega}_{s\|} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{\vphantom{\sum_{n =1}^{\infty} \left[\left( \frac{2}{k_{\bot}^2 \tilde{\rho}_s^2}+\frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - \frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]} Z\!\left(\tilde{\omega}_{s\|}\right) k_{\bot}^2 \tilde{\rho}_s^2 \left[{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]\right. \nonumber\\ &\quad \left.+\, 2 \tilde{\omega}_{s\|} k_{\|}^2 \tilde{\rho}_s^2 \sum_{n =1}^{\infty} \left[\left( \frac{2}{k_{\bot}^2 \tilde{\rho}_s^2}+\frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - \frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} &\approx \tilde{\omega}_{s\|} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{\vphantom{\sum_{n =1}^{\infty} \left[\left( \frac{2}{k_{\bot}^2 \tilde{\rho}_s^2}+\frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - \frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]} Z\!\left(\tilde{\omega}_{s\|}\right) k_{\bot}^2 \tilde{\rho}_s^2 \left[{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]\right. \nonumber\\ &\quad \left.+\, 2 \tilde{\omega}_{s\|} k_{\|}^2 \tilde{\rho}_s^2 \sum_{n =1}^{\infty} \left[\left( \frac{2}{k_{\bot}^2 \tilde{\rho}_s^2}+\frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - \frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} &\approx \mathrm{i} \tilde{\omega}_{s\|} \left[1+ \tilde{\omega}_{s\|} Z\!\left(\tilde{\omega}_{s\|}\right) \right] \nonumber\\ &\quad \times k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} &\approx \mathrm{i} \tilde{\omega}_{s\|} \left[1+ \tilde{\omega}_{s\|} Z\!\left(\tilde{\omega}_{s\|}\right) \right] \nonumber\\ &\quad \times k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
where we have again used the sum identities (G24). Note that we have retained a term in ![]() $(\boldsymbol{\mathsf{M}}_s)_{yy}$ which is quadratic in
$(\boldsymbol{\mathsf{M}}_s)_{yy}$ which is quadratic in ![]() $k_{\|} \tilde {\rho }_s$, even though there exists another term which is independent of
$k_{\|} \tilde {\rho }_s$, even though there exists another term which is independent of ![]() $k_{\|} \tilde {\rho }_s$. This is because the latter term becomes arbitrarily small in the limit
$k_{\|} \tilde {\rho }_s$. This is because the latter term becomes arbitrarily small in the limit ![]() $k_{\bot } \rho _s \ll 1$, whereas the former is independent of
$k_{\bot } \rho _s \ll 1$, whereas the former is independent of ![]() $k_{\bot } \rho _s$; hence, if
$k_{\bot } \rho _s$; hence, if ![]() $k_{\bot } \rho _s \ll k_{\|} \rho _s$, the latter term can become dominant.
$k_{\bot } \rho _s \ll k_{\|} \rho _s$, the latter term can become dominant.
Now considering the limit ![]() $\tilde {\omega }_{s\|} \ll 1$, while holding
$\tilde {\omega }_{s\|} \ll 1$, while holding ![]() $k_{\|} \rho _s \ll 1$ at some fixed value, the plasma dispersion function can now be approximated by its small-argument expansion
$k_{\|} \rho _s \ll 1$ at some fixed value, the plasma dispersion function can now be approximated by its small-argument expansion
to give
 $$\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} &\approx \frac{2 k_{\|}^2}{k_{\bot}^2} \tilde{\omega}_{s\|}^2 \left[1-\exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_s)_{xx} &\approx \frac{2 k_{\|}^2}{k_{\bot}^2} \tilde{\omega}_{s\|}^2 \left[1-\exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] , \end{align}$$ $$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xz} &\approx{-}4 k_{\|}^2 \tilde{\rho}_s^2 \frac{k_{\|}}{k_{\bot}} \tilde{\omega}_{s\|}^2 \sum_{n =1}^{\infty} \frac{1}{n^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s)_{xz} &\approx{-}4 k_{\|}^2 \tilde{\rho}_s^2 \frac{k_{\|}}{k_{\bot}} \tilde{\omega}_{s\|}^2 \sum_{n =1}^{\infty} \frac{1}{n^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$ \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} &\approx \tilde{\omega}_{s\|} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{\vphantom{\sum_{n =1}^{\infty} \left[\left( \frac{2}{k_{\bot}^2 \tilde{\rho}_s^2}+\frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - \frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]} \mathrm{i} \sqrt{\rm \pi} k_{\bot}^2 \tilde{\rho}_s^2 \left[{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]\right. \nonumber\\ &\quad \left. +\, 2 \tilde{\omega}_{s\|}^2 k_{\|}^2 \tilde{\rho}_s^2 \sum_{n =1}^{\infty} \left[\left( \frac{2}{k_{\bot}^2 \tilde{\rho}_s^2}+\frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - \frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yy} &\approx \tilde{\omega}_{s\|} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{\vphantom{\sum_{n =1}^{\infty} \left[\left( \frac{2}{k_{\bot}^2 \tilde{\rho}_s^2}+\frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - \frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]} \mathrm{i} \sqrt{\rm \pi} k_{\bot}^2 \tilde{\rho}_s^2 \left[{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]\right. \nonumber\\ &\quad \left. +\, 2 \tilde{\omega}_{s\|}^2 k_{\|}^2 \tilde{\rho}_s^2 \sum_{n =1}^{\infty} \left[\left( \frac{2}{k_{\bot}^2 \tilde{\rho}_s^2}+\frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - \frac{k_{\bot}^2 \tilde{\rho}_s^2}{n^2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} &\approx \mathrm{i} \tilde{\omega}_{s\|} \left[1+ \mathrm{i} \sqrt{\rm \pi} \tilde{\omega}_{s\|} \right] \nonumber\\ &\quad \times k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{M}}_s)_{yz} &\approx \mathrm{i} \tilde{\omega}_{s\|} \left[1+ \mathrm{i} \sqrt{\rm \pi} \tilde{\omega}_{s\|} \right] \nonumber\\ &\quad \times k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
For comparison, we state below the long-wavelength limit of ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ using asymptotic expressions (G36):
$\boldsymbol{\mathsf{M}}_s^{(0)}$ using asymptotic expressions (G36):
 $$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} &= 4 \mathrm{i} \sqrt{\rm \pi} \frac{\tilde{\omega}_{s\|} }{k_{\bot}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{1}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_s^{(0)})_{xx} &= 4 \mathrm{i} \sqrt{\rm \pi} \frac{\tilde{\omega}_{s\|} }{k_{\bot}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{1}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$ $$\begin{align}(\boldsymbol{\mathsf{M}}_s^{(0)})_{xz} &={-}4 \mathrm{i} \sqrt{\rm \pi} \frac{\tilde{\omega}_{s\|} }{k_{\bot} k_{\|} \tilde{\rho}_s^2} \exp{\left(-\frac{1}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s^{(0)})_{xz} &={-}4 \mathrm{i} \sqrt{\rm \pi} \frac{\tilde{\omega}_{s\|} }{k_{\bot} k_{\|} \tilde{\rho}_s^2} \exp{\left(-\frac{1}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}$$ $$\begin{align}(\boldsymbol{\mathsf{M}}_s^{(0)})_{zz} &= 4 \mathrm{i} \sqrt{\rm \pi} \frac{\tilde{\omega}_{s\|}}{k_{\|}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{1}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{M}}_s^{(0)})_{zz} &= 4 \mathrm{i} \sqrt{\rm \pi} \frac{\tilde{\omega}_{s\|}}{k_{\|}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{1}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_1\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align}$$
Assuming ![]() $k_{\bot } \rho _s \sim 1$, we observe that, while three of the six unique dielectric tensor components are identical for both
$k_{\bot } \rho _s \sim 1$, we observe that, while three of the six unique dielectric tensor components are identical for both ![]() $\tilde {\omega }_{s\|} \rightarrow 0$,
$\tilde {\omega }_{s\|} \rightarrow 0$, ![]() $k_{\|} \rho _s \ll 1$ fixed, and
$k_{\|} \rho _s \ll 1$ fixed, and ![]() $k_{\|} \rho _s \rightarrow 0$,
$k_{\|} \rho _s \rightarrow 0$, ![]() $\tilde {\omega }_{s\|} \ll 1$ fixed [
$\tilde {\omega }_{s\|} \ll 1$ fixed [![]() $(\boldsymbol{\mathsf{M}}_s)_{xy}$,
$(\boldsymbol{\mathsf{M}}_s)_{xy}$, ![]() $(\boldsymbol{\mathsf{M}}_s)_{yy}$, and
$(\boldsymbol{\mathsf{M}}_s)_{yy}$, and ![]() $(\boldsymbol{\mathsf{M}}_s)_{yz}$], the other three [
$(\boldsymbol{\mathsf{M}}_s)_{yz}$], the other three [![]() $(\boldsymbol{\mathsf{M}}_s)_{xx}$,
$(\boldsymbol{\mathsf{M}}_s)_{xx}$, ![]() $(\boldsymbol{\mathsf{M}}_s)_{xz}$ and
$(\boldsymbol{\mathsf{M}}_s)_{xz}$ and ![]() $(\boldsymbol{\mathsf{M}}_s)_{zz}$] are not. Instead, the dominant terms are the quadratic terms
$(\boldsymbol{\mathsf{M}}_s)_{zz}$] are not. Instead, the dominant terms are the quadratic terms ![]() $(\boldsymbol{\mathsf{M}}_s^{(1)})_{xx}$,
$(\boldsymbol{\mathsf{M}}_s^{(1)})_{xx}$, ![]() $(\boldsymbol{\mathsf{M}}_s^{(1)})_{xz}$ and
$(\boldsymbol{\mathsf{M}}_s^{(1)})_{xz}$ and ![]() $(\boldsymbol{\mathsf{M}}_s^{(1)})_{zz}$ in the
$(\boldsymbol{\mathsf{M}}_s^{(1)})_{zz}$ in the ![]() $\tilde {\omega }_{s\|} \ll 1$ expansion. In the limit
$\tilde {\omega }_{s\|} \ll 1$ expansion. In the limit ![]() $k_{\bot } \rho _s \ll 1$,
$k_{\bot } \rho _s \ll 1$, ![]() $(\boldsymbol{\mathsf{M}}_s)_{yy}$ also departs from the approximation
$(\boldsymbol{\mathsf{M}}_s)_{yy}$ also departs from the approximation ![]() $(\boldsymbol{\mathsf{M}}_s^{(0)})_{yy}$ for sufficiently small
$(\boldsymbol{\mathsf{M}}_s^{(0)})_{yy}$ for sufficiently small ![]() $k_{\bot } \rho _s$ as compared with
$k_{\bot } \rho _s$ as compared with ![]() $k_{\|} \rho _s$, instead being accurately described by
$k_{\|} \rho _s$, instead being accurately described by ![]() $(\boldsymbol{\mathsf{M}}_s^{(1)})_{yy}$.
$(\boldsymbol{\mathsf{M}}_s^{(1)})_{yy}$.
As a consequence, we must assess the conditions under which one approximation or the other is valid. This is most simply answered by observing that the expressions for ![]() $(\boldsymbol{\mathsf{M}}_s^{(0)})_{xx}$,
$(\boldsymbol{\mathsf{M}}_s^{(0)})_{xx}$, ![]() $(\boldsymbol{\mathsf{M}}_s^{(0)})_{xz}$ and
$(\boldsymbol{\mathsf{M}}_s^{(0)})_{xz}$ and ![]() $(\boldsymbol{\mathsf{M}}_s^{(0)})_{zz}$ from (G59a), (G59c) and (G59f) are exponentially small; thus, for
$(\boldsymbol{\mathsf{M}}_s^{(0)})_{zz}$ from (G59a), (G59c) and (G59f) are exponentially small; thus, for ![]() $k_{\|} \rho _s \ll 1/\log {(1/\tilde {\omega }_{s\|})}$, we must use approximations (G58a), (G58c), (G58e) for
$k_{\|} \rho _s \ll 1/\log {(1/\tilde {\omega }_{s\|})}$, we must use approximations (G58a), (G58c), (G58e) for ![]() $(\boldsymbol{\mathsf{M}}_s)_{xx}$,
$(\boldsymbol{\mathsf{M}}_s)_{xx}$, ![]() $(\boldsymbol{\mathsf{M}}_s)_{xz}$ and
$(\boldsymbol{\mathsf{M}}_s)_{xz}$ and ![]() $(\boldsymbol{\mathsf{M}}_s)_{zz}$. In addition, if
$(\boldsymbol{\mathsf{M}}_s)_{zz}$. In addition, if ![]() $k_{\bot }^2 \rho _s^2 \ll \tilde {\omega }_{s\|} k_{\|}^2 \rho _s^2 \ll 1$, then
$k_{\bot }^2 \rho _s^2 \ll \tilde {\omega }_{s\|} k_{\|}^2 \rho _s^2 \ll 1$, then
becomes the appropriate approximation for ![]() $(\boldsymbol{\mathsf{M}}_s)_{yy}$.
$(\boldsymbol{\mathsf{M}}_s)_{yy}$.
G.1.7. Calculation of second-order corrections to dispersion relation
In this appendix, we justify the relations (K20) used in Appendix K – that is, for ![]() $k_{\|} \rho _s \ll 1$,
$k_{\|} \rho _s \ll 1$,
 $$\begin{align} \frac{\left[(\boldsymbol{\mathsf{M}}_{s})_{13}\right]^2}{(\boldsymbol{\mathsf{M}}_s^{(1)})_{33}} &\lesssim (\boldsymbol{\mathsf{M}}_{s})_{11} , \end{align}$$
$$\begin{align} \frac{\left[(\boldsymbol{\mathsf{M}}_{s})_{13}\right]^2}{(\boldsymbol{\mathsf{M}}_s^{(1)})_{33}} &\lesssim (\boldsymbol{\mathsf{M}}_{s})_{11} , \end{align}$$ $$\begin{align}\frac{\left[(\boldsymbol{\mathsf{M}}_{s})_{23}\right]^2}{(\boldsymbol{\mathsf{M}}_s^{(1)})_{33}} &\lesssim \tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{s})_{22} \ll (\boldsymbol{\mathsf{M}}_{s})_{22} . \end{align}$$
$$\begin{align}\frac{\left[(\boldsymbol{\mathsf{M}}_{s})_{23}\right]^2}{(\boldsymbol{\mathsf{M}}_s^{(1)})_{33}} &\lesssim \tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{s})_{22} \ll (\boldsymbol{\mathsf{M}}_{s})_{22} . \end{align}$$We also prove the identity (K25), or
 \begin{equation} (\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} - \frac{\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}\right]^2}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} ={-}\frac{4}{3} W_e - \frac{4}{3} W_i - \frac{1}{4} \left(L_e + L_i\right)^2 ,\end{equation}
\begin{equation} (\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} - \frac{\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}\right]^2}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} ={-}\frac{4}{3} W_e - \frac{4}{3} W_i - \frac{1}{4} \left(L_e + L_i\right)^2 ,\end{equation}
used to derive the dispersion relation (K23). We have introduced the notation ![]() $W_e = W(k_{\|} \tilde {\rho }_e,k_{\bot } \tilde {\rho }_e )$,
$W_e = W(k_{\|} \tilde {\rho }_e,k_{\bot } \tilde {\rho }_e )$, ![]() $W_i = L(k_{\|} \rho _i,k_{\bot } \rho _i )$,
$W_i = L(k_{\|} \rho _i,k_{\bot } \rho _i )$, ![]() $L_e = L(k_{\|} \tilde {\rho }_e,k_{\bot } \tilde {\rho }_e )$ and
$L_e = L(k_{\|} \tilde {\rho }_e,k_{\bot } \tilde {\rho }_e )$ and ![]() $L_i = L(k_{\|} \rho _i,k_{\bot } \rho _i )$, for the sake of brevity.
$L_i = L(k_{\|} \rho _i,k_{\bot } \rho _i )$, for the sake of brevity.
To complete the first task, we begin with the expressions (K16) for the dielectric components, and substitute (G26a), (G25b), (G25d) and (G26d) for ![]() $(\boldsymbol{\mathsf{M}}_{s}^{(1)})_{xx}$,
$(\boldsymbol{\mathsf{M}}_{s}^{(1)})_{xx}$, ![]() $(\boldsymbol{\mathsf{M}}_{s}^{(0)})_{xy}$,
$(\boldsymbol{\mathsf{M}}_{s}^{(0)})_{xy}$, ![]() $(\boldsymbol{\mathsf{M}}_{s}^{(0)})_{xy}$,
$(\boldsymbol{\mathsf{M}}_{s}^{(0)})_{xy}$, ![]() $(\boldsymbol{\mathsf{M}}_{s}^{(0)})_{yy}$ and
$(\boldsymbol{\mathsf{M}}_{s}^{(0)})_{yy}$ and ![]() $(\boldsymbol{\mathsf{M}}_{s}^{(1)})_{xy}$, respectively. This gives (K16) directly in terms of special functions
$(\boldsymbol{\mathsf{M}}_{s}^{(1)})_{xy}$, respectively. This gives (K16) directly in terms of special functions ![]() $G(x,y)$,
$G(x,y)$, ![]() $H(x,y)$,
$H(x,y)$, ![]() $L(x,y)$,
$L(x,y)$, ![]() $N(x,y)$,
$N(x,y)$, ![]() $W(x,y)$ and
$W(x,y)$ and ![]() ${Y}(x,y)$:
${Y}(x,y)$:
 $$\begin{align} (\boldsymbol{\mathsf{M}}_{s})_{11} &\approx{-}\frac{4 k^2} {3 k_{\|}^2} \tilde{\omega}_{s\|}^2 W\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right) + 2 \tilde{\omega}_{s\|}^2 \left[\frac{k_{\bot}^2}{k^2} + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_{s})_{11} &\approx{-}\frac{4 k^2} {3 k_{\|}^2} \tilde{\omega}_{s\|}^2 W\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right) + 2 \tilde{\omega}_{s\|}^2 \left[\frac{k_{\bot}^2}{k^2} + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] , \end{align}$$
We then apply the ![]() $k_{\|} \rho _s \ll 1$ limits of the aforementioned special functions using Appendices G.1.4 and G.4.2 – in particular, (G36b), (G36c), (G36d), (G36e), (G100a) and (G101c):
$k_{\|} \rho _s \ll 1$ limits of the aforementioned special functions using Appendices G.1.4 and G.4.2 – in particular, (G36b), (G36c), (G36d), (G36e), (G100a) and (G101c):
We can now make the relevant comparisons presented in (G61), and obtain the desired results
where we used the inequalities
valid for arbitrary values of ![]() $k_{\bot } \tilde {\rho }_s$.
$k_{\bot } \tilde {\rho }_s$.
To derive (G62), we use (G63a), (G63b) and (G63f) to derive the following expressions:
 $$\begin{align} (\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} &= \frac{k^2} {k_{\|}^2}\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)})_{xx} + (\boldsymbol{\mathsf{M}}_{i}^{(1)})_{xx} \right] + 2 \left[\frac{2 k_{\bot}^2}{k^2} + \frac{k_{\bot}}{k_{\|}} \left( L_e + L_i \right)\right], \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} &= \frac{k^2} {k_{\|}^2}\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)})_{xx} + (\boldsymbol{\mathsf{M}}_{i}^{(1)})_{xx} \right] + 2 \left[\frac{2 k_{\bot}^2}{k^2} + \frac{k_{\bot}}{k_{\|}} \left( L_e + L_i \right)\right], \end{align}$$Then
 \begin{equation} \frac{\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}\right]^2}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} = \left[\frac{2 k_{\bot}}{k} + \frac{k}{2 k_{\|}} \left( L_e + L_i\right) \right]^2 , \end{equation}
\begin{equation} \frac{\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}\right]^2}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} = \left[\frac{2 k_{\bot}}{k} + \frac{k}{2 k_{\|}} \left( L_e + L_i\right) \right]^2 , \end{equation}which in turn gives
 \begin{equation} (\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} - \frac{\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}\right]^2}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} = \frac{k^2} {k_{\|}^2}\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)})_{xx} + (\boldsymbol{\mathsf{M}}_{i}^{(1)})_{xx} - \frac{1}{4} \left(L_e + L_i\right)^2\right] . \end{equation}
\begin{equation} (\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} - \frac{\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}\right]^2}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} = \frac{k^2} {k_{\|}^2}\left[(\boldsymbol{\mathsf{M}}_{e}^{(1)})_{xx} + (\boldsymbol{\mathsf{M}}_{i}^{(1)})_{xx} - \frac{1}{4} \left(L_e + L_i\right)^2\right] . \end{equation}G.2. The CE electron-friction term
For an electron distribution of the form
with ![]() $\eta _s^{R} \ll 1$ a constant, it follows that
$\eta _s^{R} \ll 1$ a constant, it follows that
while
Since
when ![]() $\varLambda _e(\tilde {v}_{e\|},\tilde {v}_{e\bot })$ is given by (G71), the function
$\varLambda _e(\tilde {v}_{e\|},\tilde {v}_{e\bot })$ is given by (G71), the function ![]() $\varXi _e(\tilde {v}_{e\|},\tilde {v}_{e\bot })$ is just proportional to that arising for a Maxwellian distribution (cf. (G13)), and so the dielectric response associated with the CE electron-friction term is
$\varXi _e(\tilde {v}_{e\|},\tilde {v}_{e\bot })$ is just proportional to that arising for a Maxwellian distribution (cf. (G13)), and so the dielectric response associated with the CE electron-friction term is
G.3. The CE temperature-gradient-driven terms
For the CE temperature-gradient-driven term arising from a Krook operator, which takes the form
it follows (assuming ![]() $\eta _e^R = 0$) that
$\eta _e^R = 0$) that
and
Then, to leading order in ![]() $\eta _s$,
$\eta _s$,
 \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xx} & = \frac{2}{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}\right]}\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xx} & = \frac{2}{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}\right]}\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xy} & = \frac{2 \mathrm{i}}{\sqrt{\rm \pi}} \eta_s\sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right)\left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xy} & = \frac{2 \mathrm{i}}{\sqrt{\rm \pi}} \eta_s\sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right)\left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xz} & = \frac{2}{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xz} & = \frac{2}{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \end{align} \begin{align} & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}} \right] , \end{align}
\begin{align} & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}} \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{yy} & = \frac{2}{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^3 {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} } \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{yy} & = \frac{2}{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^3 {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} } \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{yz} & ={-}\frac{2 \mathrm{i} }{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \quad \left. \times\, \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} } \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{yz} & ={-}\frac{2 \mathrm{i} }{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \quad \left. \times\, \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right) \vphantom{\int_{C_L} \frac{\exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} } \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{zz} & = \frac{2 }{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right)\vphantom{\int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}} \right] . \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{zz} & = \frac{2 }{\sqrt{\rm \pi}} \eta_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \left(\tilde{v}_{s}^2 - \frac{5}{2}\right)\vphantom{\int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}} \right] . \end{align}In addition to the plasma-dispersion-function identities (G15) and Bessel-function identities (G16), we use
and
 \begin{align} \int_0^{\infty} \mathrm{d} t \, t^3 {J}_n(\alpha t)^2 \exp \left({-}t^2\right)& = \frac{1}{2} \exp \left(-\frac{\alpha^2}{2}\right) \left\{{I}_n\!\left(\frac{\alpha^2}{2}\right) \right. \nonumber\\ & \left.\quad +\, \frac{\alpha^2}{2} \left[{I}_n'\!\left(\frac{\alpha^2}{2}\right) - {I}_n\! \left(\frac{\alpha^2}{2}\right)\right]\right\} , \end{align}
\begin{align} \int_0^{\infty} \mathrm{d} t \, t^3 {J}_n(\alpha t)^2 \exp \left({-}t^2\right)& = \frac{1}{2} \exp \left(-\frac{\alpha^2}{2}\right) \left\{{I}_n\!\left(\frac{\alpha^2}{2}\right) \right. \nonumber\\ & \left.\quad +\, \frac{\alpha^2}{2} \left[{I}_n'\!\left(\frac{\alpha^2}{2}\right) - {I}_n\! \left(\frac{\alpha^2}{2}\right)\right]\right\} , \end{align} \begin{align} \int_0^{\infty} \mathrm{d} t^4 \, t^2 {J}_n(\alpha t) {J}_n'(\alpha t) \exp \left({-}t^2\right) & = \frac{\alpha}{4} \exp \left(-\frac{\alpha^2}{2}\right) \left[ \left(\alpha^2-2 + \frac{2 n^2}{\alpha^2} \right) {I}_n\!\left(\frac{\alpha^2}{2}\right)\right. \nonumber\\ & \quad \left. +\, \left(1-\alpha^2 \right) {I}_n'\!\left(\frac{\alpha^2}{2}\right) \right] , \end{align}
\begin{align} \int_0^{\infty} \mathrm{d} t^4 \, t^2 {J}_n(\alpha t) {J}_n'(\alpha t) \exp \left({-}t^2\right) & = \frac{\alpha}{4} \exp \left(-\frac{\alpha^2}{2}\right) \left[ \left(\alpha^2-2 + \frac{2 n^2}{\alpha^2} \right) {I}_n\!\left(\frac{\alpha^2}{2}\right)\right. \nonumber\\ & \quad \left. +\, \left(1-\alpha^2 \right) {I}_n'\!\left(\frac{\alpha^2}{2}\right) \right] , \end{align} \begin{align} \int_0^{\infty} \mathrm{d} t^5 \, t^3 {J}_n'(\alpha t)^2 \exp \left({-}t^2\right) & = \frac{1}{2} \exp \left(-\frac{\alpha^2}{2}\right) \nonumber\\ & \quad \times \left\{\left[\frac{3 \alpha^2 }{2} - \frac{\alpha^4}{2} + n^2 \left(\frac{1}{\alpha^2} -\frac{3}{2}\right) \right] {I}_n\!\left(\frac{\alpha^2}{2}\right)\right. \nonumber\\ & \quad +\left. \left( \frac{\alpha^4}{2} + \frac{n^2}{2} - \alpha^2 \right) {I}_n'\!\left(\frac{\alpha^2}{2}\right) \right\} , \end{align}
\begin{align} \int_0^{\infty} \mathrm{d} t^5 \, t^3 {J}_n'(\alpha t)^2 \exp \left({-}t^2\right) & = \frac{1}{2} \exp \left(-\frac{\alpha^2}{2}\right) \nonumber\\ & \quad \times \left\{\left[\frac{3 \alpha^2 }{2} - \frac{\alpha^4}{2} + n^2 \left(\frac{1}{\alpha^2} -\frac{3}{2}\right) \right] {I}_n\!\left(\frac{\alpha^2}{2}\right)\right. \nonumber\\ & \quad +\left. \left( \frac{\alpha^4}{2} + \frac{n^2}{2} - \alpha^2 \right) {I}_n'\!\left(\frac{\alpha^2}{2}\right) \right\} , \end{align}to obtain again the expressions for the dielectric components (G78) in terms of special mathematical functions (a tedious, but elementary calculation):
 \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xx} & = \eta_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} Z\!\left(\zeta_{sn}\right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \left.\quad +\, \left[\zeta_{sn} + Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xx} & = \eta_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} Z\!\left(\zeta_{sn}\right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \left.\quad +\, \left[\zeta_{sn} + Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xy} & = \frac{\mathrm{i} \eta_s}{2} \sum_{n={-}\infty}^{\infty} n \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \left[ \zeta_{sn} + Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \left.\quad +\, \left[Z\!\left(\zeta_{sn}\right) \left(\frac{1}{2} +\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}-\zeta_{sn}^2 \right) -\zeta_{sn} \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xy} & = \frac{\mathrm{i} \eta_s}{2} \sum_{n={-}\infty}^{\infty} n \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \left[ \zeta_{sn} + Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \left.\quad +\, \left[Z\!\left(\zeta_{sn}\right) \left(\frac{1}{2} +\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}-\zeta_{sn}^2 \right) -\zeta_{sn} \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xz} & = \eta_s \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \left[1 + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\left.\quad +\, \left[\zeta_{sn}^2 - 1 -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xz} & = \eta_s \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \left[1 + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\left.\quad +\, \left[\zeta_{sn}^2 - 1 -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{yy} & = \eta_s \sum_{n={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \left[ \left(\frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \right)\zeta_{sn}\right.\right. \nonumber\\ &\quad \left.\left. + Z\!\left(\zeta_{sn}\right)\left(\frac{n^2 \zeta_{sn}^2}{k_{\bot}^2 \tilde{\rho}_s^2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2 \zeta_{sn}^2}{2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{4} - \frac{k_{\bot}^4 \tilde{\rho}_s^4}{2} - \frac{3 n^2}{2} - \frac{3 n^2}{2 k_{\bot}^2 \tilde{\rho}_s^2} \right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ &\quad + \left[Z\!\left(\zeta_{sn}\right) \left(\frac{1}{2} + k_{\bot}^2 \tilde{\rho}_s^2 + \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \zeta_{sn}^2 \right) - \zeta_{sn} \right] \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{yy} & = \eta_s \sum_{n={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \left[ \left(\frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \right)\zeta_{sn}\right.\right. \nonumber\\ &\quad \left.\left. + Z\!\left(\zeta_{sn}\right)\left(\frac{n^2 \zeta_{sn}^2}{k_{\bot}^2 \tilde{\rho}_s^2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2 \zeta_{sn}^2}{2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{4} - \frac{k_{\bot}^4 \tilde{\rho}_s^4}{2} - \frac{3 n^2}{2} - \frac{3 n^2}{2 k_{\bot}^2 \tilde{\rho}_s^2} \right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ &\quad + \left[Z\!\left(\zeta_{sn}\right) \left(\frac{1}{2} + k_{\bot}^2 \tilde{\rho}_s^2 + \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \zeta_{sn}^2 \right) - \zeta_{sn} \right] \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{yz} & ={-}\frac{\mathrm{i} \eta_s}{2} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\nonumber\\ &\quad \times \left\{ \left[k_{\bot}^2 \tilde{\rho}_s^2 + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \zeta_{sn}^2 + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \left(k_{\bot}^2 \tilde{\rho}_s^2 + \frac{1}{2} + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \zeta_{sn}^2\right)\right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad \left. +\, \left[\zeta_{sn}^2 -1 - k_{\bot}^2 \tilde{\rho}_s^2 + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} - k_{\bot}^2 \tilde{\rho}_s^2\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{yz} & ={-}\frac{\mathrm{i} \eta_s}{2} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\nonumber\\ &\quad \times \left\{ \left[k_{\bot}^2 \tilde{\rho}_s^2 + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \zeta_{sn}^2 + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \left(k_{\bot}^2 \tilde{\rho}_s^2 + \frac{1}{2} + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \zeta_{sn}^2\right)\right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad \left. +\, \left[\zeta_{sn}^2 -1 - k_{\bot}^2 \tilde{\rho}_s^2 + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} - k_{\bot}^2 \tilde{\rho}_s^2\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{zz} & = \eta_s \sum_{n={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \zeta_{sn} \left[1 + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad \left.+\, \left[\zeta_{sn}^3 - \zeta_{sn} -\frac{k_{\bot}^2 \tilde{\rho}_s^2 \zeta_{sn}}{2} + \zeta_{sn}^2 Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right\} . \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{zz} & = \eta_s \sum_{n={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \zeta_{sn} \left[1 + \zeta_{sn} Z\!\left(\zeta_{sn}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad \left.+\, \left[\zeta_{sn}^3 - \zeta_{sn} -\frac{k_{\bot}^2 \tilde{\rho}_s^2 \zeta_{sn}}{2} + \zeta_{sn}^2 Z\!\left(\zeta_{sn}\right) \left(\zeta_{sn}^2 - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right\} . \end{align}G.3.1. Dielectric tensor in low-frequency limit
In the low-frequency limit ![]() $\tilde {\omega }_{s\|} \ll 1$ under the ordering
$\tilde {\omega }_{s\|} \ll 1$ under the ordering ![]() $k_{\|} \rho _s \sim k_{\bot } \rho _s \sim 1$, the expressions (G81) can be approximated by the leading-order term of the expansion of
$k_{\|} \rho _s \sim k_{\bot } \rho _s \sim 1$, the expressions (G81) can be approximated by the leading-order term of the expansion of ![]() $\boldsymbol{\mathsf{P}}_s$, that is
$\boldsymbol{\mathsf{P}}_s$, that is
where
 \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xx} & = \eta_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad \left. +\, \left[-\frac{n}{|k_{\|}| \tilde{\rho}_s} + Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}, \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xx} & = \eta_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad \left. +\, \left[-\frac{n}{|k_{\|}| \tilde{\rho}_s} + Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}, \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xy} & = \frac{\mathrm{i} \eta_s}{2} \sum_{n={-}\infty}^{\infty} n \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ &\quad \times \left\{ \left[Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{1}{2} +\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}-\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right) + \frac{n}{|k_{\|}| \tilde{\rho}_s}\right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad \left. +\, \left[ -\frac{n}{|k_{\|}| \tilde{\rho}_s} + Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xy} & = \frac{\mathrm{i} \eta_s}{2} \sum_{n={-}\infty}^{\infty} n \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ &\quad \times \left\{ \left[Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{1}{2} +\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}-\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} \right) + \frac{n}{|k_{\|}| \tilde{\rho}_s}\right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad \left. +\, \left[ -\frac{n}{|k_{\|}| \tilde{\rho}_s} + Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xz} & = \eta_s \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \left[1 -\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad + {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - 1 -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right. \nonumber\\ & \quad \left.\left.-\,\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xz} & = \eta_s \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \left[1 -\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad + {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - 1 -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right. \nonumber\\ & \quad \left.\left.-\,\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{|k_{\|}|^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yy} & = \eta_s \sum_{n={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \left[ -\left(\frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \right)\frac{n}{|k_{\|}| \tilde{\rho}_s}\right.\right. \nonumber\\ & \quad + Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\left(\frac{n^4}{k_{\bot}^2 k_{\|}^2 \tilde{\rho}_s^4} + \frac{n^2 k_{\bot}^2}{k_{\|}^2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{4} - \frac{k_{\bot}^4 \tilde{\rho}_s^4}{2} \right. \nonumber \\ & \quad \left.\left. - \frac{3 n^2}{2} - \frac{3 n^2}{2 k_{\bot}^2 \tilde{\rho}_s^2} \right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & \quad \left.\times\, \left[Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{1}{2} + k_{\bot}^2 \tilde{\rho}_s^2 + \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} -\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \right) +\frac{n}{|k_{\|}| \tilde{\rho}_s} \right] \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yy} & = \eta_s \sum_{n={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ \left[ -\left(\frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} \right)\frac{n}{|k_{\|}| \tilde{\rho}_s}\right.\right. \nonumber\\ & \quad + Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\left(\frac{n^4}{k_{\bot}^2 k_{\|}^2 \tilde{\rho}_s^4} + \frac{n^2 k_{\bot}^2}{k_{\|}^2} + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{4} - \frac{k_{\bot}^4 \tilde{\rho}_s^4}{2} \right. \nonumber \\ & \quad \left.\left. - \frac{3 n^2}{2} - \frac{3 n^2}{2 k_{\bot}^2 \tilde{\rho}_s^2} \right) \right] {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & \quad \left.\times\, \left[Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{1}{2} + k_{\bot}^2 \tilde{\rho}_s^2 + \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} -\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \right) +\frac{n}{|k_{\|}| \tilde{\rho}_s} \right] \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yz} & ={-}\frac{\mathrm{i} \eta_s}{2} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & \quad \times \left\{ {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[k_{\bot}^2 \tilde{\rho}_s^2 + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} -\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right.\right.\nonumber\\ & \quad \left.-\,\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(k_{\bot}^2 \tilde{\rho}_s^2 + \frac{1}{2} + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)\right]\nonumber\\ & \quad + {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} -1 - k_{\bot}^2 \tilde{\rho}_s^2 \right. \nonumber\\ & \left.\left.\quad -\,\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} - k_{\bot}^2 \tilde{\rho}_s^2\right) \right] \right\} , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yz} & ={-}\frac{\mathrm{i} \eta_s}{2} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & \quad \times \left\{ {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[k_{\bot}^2 \tilde{\rho}_s^2 + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} -\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right.\right.\nonumber\\ & \quad \left.-\,\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(k_{\bot}^2 \tilde{\rho}_s^2 + \frac{1}{2} + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)\right]\nonumber\\ & \quad + {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} -1 - k_{\bot}^2 \tilde{\rho}_s^2 \right. \nonumber\\ & \left.\left.\quad -\,\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} - k_{\bot}^2 \tilde{\rho}_s^2\right) \right] \right\} , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{zz} & = \eta_s \sum_{n={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ -\frac{n k_{\bot}^2 \tilde{\rho}_s}{2 |k_{\|}|} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad + {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\frac{n}{|k_{\|}| \tilde{\rho}_s} -\frac{n^3}{|k_{\|}|^3 \tilde{\rho}_s^3} +\frac{n k_{\bot}^2 \tilde{\rho}_s}{2 |k_{\|}|}\right. \nonumber\\ &\quad\left.\left. + \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} Z\!\left( - \frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\} . \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{zz} & = \eta_s \sum_{n={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left\{ -\frac{n k_{\bot}^2 \tilde{\rho}_s}{2 |k_{\|}|} \left[1 - \frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ &\quad + {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\frac{n}{|k_{\|}| \tilde{\rho}_s} -\frac{n^3}{|k_{\|}|^3 \tilde{\rho}_s^3} +\frac{n k_{\bot}^2 \tilde{\rho}_s}{2 |k_{\|}|}\right. \nonumber\\ &\quad\left.\left. + \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} Z\!\left( - \frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \right\} . \end{align}
In this limit, we have utilised the approximation ![]() $\zeta _{sn} \approx - n/|k_{\|}| \tilde {\rho }_s$. Similarly to the Maxwellian case, we can use the Bessel-function-summation identities (G24) and the symmetry properties of the plasma dispersion function with a real argument to show that
$\zeta _{sn} \approx - n/|k_{\|}| \tilde {\rho }_s$. Similarly to the Maxwellian case, we can use the Bessel-function-summation identities (G24) and the symmetry properties of the plasma dispersion function with a real argument to show that
 \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xx} & = 2 \mathrm{i} \sqrt{\rm \pi} \eta_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n=1}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \left[\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right){I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] \nonumber\\ & = \mathrm{i} \eta_s {I}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xx} & = 2 \mathrm{i} \sqrt{\rm \pi} \eta_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n=1}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \left[\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right){I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] \nonumber\\ & = \mathrm{i} \eta_s {I}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xy} & ={-}\mathrm{i} \eta_s \left\{\frac{1}{2 |k_{\|}| \tilde{\rho}_s} + \frac{1}{2} \sum_{n={-}\infty}^{\infty} n \, {\rm Re}{\left[Z\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \times \left\{\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} - k_{\bot}^2 \tilde{\rho}_s^2 \right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad\left. +\left(\frac{1}{2} + k_{\bot}^2 \tilde{\rho}_s^2 + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}\nonumber\\ & ={-}\mathrm{i} \eta_s {J}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) ,\end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xy} & ={-}\mathrm{i} \eta_s \left\{\frac{1}{2 |k_{\|}| \tilde{\rho}_s} + \frac{1}{2} \sum_{n={-}\infty}^{\infty} n \, {\rm Re}{\left[Z\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \times \left\{\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} - k_{\bot}^2 \tilde{\rho}_s^2 \right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad\left. +\left(\frac{1}{2} + k_{\bot}^2 \tilde{\rho}_s^2 + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}\nonumber\\ & ={-}\mathrm{i} \eta_s {J}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) ,\end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xz} & ={-}2 \mathrm{i} \sqrt{\rm \pi} \eta_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n=1}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{n^2}{|k_{\|}| k_{\bot} \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \left[\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right){I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] \nonumber\\ & ={-}\frac{\mathrm{i} k_{\bot}}{|k_{\|}|} \eta_s {I}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xz} & ={-}2 \mathrm{i} \sqrt{\rm \pi} \eta_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n=1}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{n^2}{|k_{\|}| k_{\bot} \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \left[\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right){I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] \nonumber\\ & ={-}\frac{\mathrm{i} k_{\bot}}{|k_{\|}|} \eta_s {I}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yy} & = \frac{\mathrm{i} \sqrt{\rm \pi}}{2} \eta_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \left\{\left(n^2 + \frac{1}{2} k_{\bot}^2 \tilde{\rho}_s^2 + k_{\bot}^4 \tilde{\rho}_s^4 - \frac{n^2 k_{\bot}^2}{k_{\|}^2}\right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \left.+\,\left(\frac{2 n^4}{k_{\|}^2 k_{\bot}^2 \tilde{\rho}_s^4} - \frac{3 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - 3 n^2 + \frac{1}{2} k_{\bot}^2 \tilde{\rho}_s^2 - k_{\bot}^4 \tilde{\rho}_s^4 + \frac{n^2 k_{\bot}^2}{k_{\|}^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ & = \mathrm{i} \eta_s {K}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yy} & = \frac{\mathrm{i} \sqrt{\rm \pi}}{2} \eta_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \left\{\left(n^2 + \frac{1}{2} k_{\bot}^2 \tilde{\rho}_s^2 + k_{\bot}^4 \tilde{\rho}_s^4 - \frac{n^2 k_{\bot}^2}{k_{\|}^2}\right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \left.+\,\left(\frac{2 n^4}{k_{\|}^2 k_{\bot}^2 \tilde{\rho}_s^4} - \frac{3 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - 3 n^2 + \frac{1}{2} k_{\bot}^2 \tilde{\rho}_s^2 - k_{\bot}^4 \tilde{\rho}_s^4 + \frac{n^2 k_{\bot}^2}{k_{\|}^2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ & = \mathrm{i} \eta_s {K}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yz} & ={-}\mathrm{i} \eta_s \left\{\frac{k_{\bot}}{2 k_{\|}^2 \tilde{\rho}_s} + \frac{1}{2} \sum_{n={-}\infty}^{\infty} \frac{n k_{\bot}}{|k_{\|}|} \, {\rm Re}{\left[Z\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \times \left\{\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} - k_{\bot}^2 \tilde{\rho}_s^2 \right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \left. +\left(\frac{1}{2} + k_{\bot}^2 \tilde{\rho}_s^2 + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}\nonumber\\ & ={-}\frac{\mathrm{i} k_{\bot}}{|k_{\|}|} \eta_s {J}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yz} & ={-}\mathrm{i} \eta_s \left\{\frac{k_{\bot}}{2 k_{\|}^2 \tilde{\rho}_s} + \frac{1}{2} \sum_{n={-}\infty}^{\infty} \frac{n k_{\bot}}{|k_{\|}|} \, {\rm Re}{\left[Z\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right]} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \times \left\{\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} - k_{\bot}^2 \tilde{\rho}_s^2 \right) {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \left. +\left(\frac{1}{2} + k_{\bot}^2 \tilde{\rho}_s^2 + \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2} - \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\}\nonumber\\ & ={-}\frac{\mathrm{i} k_{\bot}}{|k_{\|}|} \eta_s {J}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{zz} & = 2 \mathrm{i} \sqrt{\rm \pi} \eta_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n=1}^{\infty} \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \left[\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right){I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] \nonumber\\ & = \frac{\mathrm{i} k_{\bot}^2}{k_{\|}^2} \eta_s {I}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{zz} & = 2 \mathrm{i} \sqrt{\rm \pi} \eta_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n=1}^{\infty} \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \left[\left(\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} - \frac{3}{2} -\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right){I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) + \frac{k_{\bot}^2 \tilde{\rho}_s^2}{2} {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right] \nonumber\\ & = \frac{\mathrm{i} k_{\bot}^2}{k_{\|}^2} \eta_s {I}\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}
where the functions ![]() ${I}(x,y)$,
${I}(x,y)$, ![]() ${J}(x,y)$ and
${J}(x,y)$ and ![]() ${K}(x,y)$ are defined by
${K}(x,y)$ are defined by
 \begin{align} {I}\!\left(x,y\right) & \equiv \frac{2 \sqrt{\rm \pi}}{y^2} \exp{\left(-\frac{y^2}{2}\right)} \nonumber\\ & \quad \times \sum_{m=1}^{\infty} m^2 \exp{\left(-\frac{m^2}{x^2}\right)} \left[\frac{y^2}{2} {I}_m'\!\left(\frac{y^2}{2}\right)+ \left(\frac{m^2}{x^2}-\frac{3+y^2}{2}\right){I}_m\!\left(\frac{y^2}{2}\right)\right] ,\end{align}
\begin{align} {I}\!\left(x,y\right) & \equiv \frac{2 \sqrt{\rm \pi}}{y^2} \exp{\left(-\frac{y^2}{2}\right)} \nonumber\\ & \quad \times \sum_{m=1}^{\infty} m^2 \exp{\left(-\frac{m^2}{x^2}\right)} \left[\frac{y^2}{2} {I}_m'\!\left(\frac{y^2}{2}\right)+ \left(\frac{m^2}{x^2}-\frac{3+y^2}{2}\right){I}_m\!\left(\frac{y^2}{2}\right)\right] ,\end{align} \begin{align} {J}\!\left(x,y\right) & \equiv \frac{1}{2x} + \frac{1}{2} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} \left\{ m \, {\rm Re}{\,Z\!\left(\frac{m}{x}\right)} \left[\left(\frac{m^2}{x^2} - \frac{3}{2} - y^2\right) {I}_m'\!\left(\frac{y^2}{2}\right) \right.\right. \nonumber\\ &\quad \left. \left. + \left(\frac{1}{2}+y^2 +\frac{2m^2}{y^2}-\frac{m^2}{x^2}\right){I}_m\!\left(\frac{y^2}{2}\right)\right] \right\} , \end{align}
\begin{align} {J}\!\left(x,y\right) & \equiv \frac{1}{2x} + \frac{1}{2} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} \left\{ m \, {\rm Re}{\,Z\!\left(\frac{m}{x}\right)} \left[\left(\frac{m^2}{x^2} - \frac{3}{2} - y^2\right) {I}_m'\!\left(\frac{y^2}{2}\right) \right.\right. \nonumber\\ &\quad \left. \left. + \left(\frac{1}{2}+y^2 +\frac{2m^2}{y^2}-\frac{m^2}{x^2}\right){I}_m\!\left(\frac{y^2}{2}\right)\right] \right\} , \end{align} \begin{align} {K}\!\left(x,y\right) & \equiv \frac{\sqrt{\rm \pi}}{2} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} \left\{\exp{\left(-\frac{m^2}{x^2}\right)} \left[\left(m^2 + \frac{1}{2}y^2 +y^4 - \frac{m^2 y^2}{x^2}\right) {I}_m'\!\left(\frac{y^2}{2}\right) \right. \right. \nonumber\\ &\quad \left. \left. + \left(\frac{2m^4}{x^2 y^2} - \frac{3~m^2}{y^2}-3~m^2+\frac{1}{2}y^2 - y^4 + \frac{m^2 y^2}{x^2}\right){I}_m\!\left(\frac{y^2}{2}\right)\right] \right\} . \end{align}
\begin{align} {K}\!\left(x,y\right) & \equiv \frac{\sqrt{\rm \pi}}{2} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} \left\{\exp{\left(-\frac{m^2}{x^2}\right)} \left[\left(m^2 + \frac{1}{2}y^2 +y^4 - \frac{m^2 y^2}{x^2}\right) {I}_m'\!\left(\frac{y^2}{2}\right) \right. \right. \nonumber\\ &\quad \left. \left. + \left(\frac{2m^4}{x^2 y^2} - \frac{3~m^2}{y^2}-3~m^2+\frac{1}{2}y^2 - y^4 + \frac{m^2 y^2}{x^2}\right){I}_m\!\left(\frac{y^2}{2}\right)\right] \right\} . \end{align}G.3.2. Asymptotic limits of  $\boldsymbol{\mathsf{P}}_s^{(0)}$
$\boldsymbol{\mathsf{P}}_s^{(0)}$
In this appendix, we give simplified expressions in the limits of small and large ![]() $x$ and
$x$ and ![]() $y$ for the special functions
$y$ for the special functions ![]() ${I}(x,y)$,
${I}(x,y)$, ![]() ${J}(x,y)$ and
${J}(x,y)$ and ![]() ${K}(x,y)$ defined by (G85). Physically, this corresponds, via (J2), to considering the dielectric response associated with
${K}(x,y)$ defined by (G85). Physically, this corresponds, via (J2), to considering the dielectric response associated with ![]() $\boldsymbol{\mathsf{P}}_s^{(0)}$ for modes with parallel and perpendicular wavenumbers that are very small or very large with respect to the inverse Larmor radius of species
$\boldsymbol{\mathsf{P}}_s^{(0)}$ for modes with parallel and perpendicular wavenumbers that are very small or very large with respect to the inverse Larmor radius of species ![]() $s$.
$s$.
Proceeding systematically through various limits, we have the following results:
(i)
 $x \sim 1$,
$x \sim 1$,  $y \ll 1$
(G86a)
$y \ll 1$
(G86a) $$\begin{align} {I}\!\left(x,y\right) &= \frac{\sqrt{\rm \pi}}{2} \left(\frac{1}{x^2}-\frac{1}{2}\right)\exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G86b)
$$\begin{align} {I}\!\left(x,y\right) &= \frac{\sqrt{\rm \pi}}{2} \left(\frac{1}{x^2}-\frac{1}{2}\right)\exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G86b) $$\begin{align}{J}\!\left(x,y\right) &= \left[\left(\frac{1}{4}-\frac{1}{2 x^2}\right){\rm Re}{\,Z\left(\frac{1}{x}\right)} + \frac{1}{2 x} \right] \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G86c)
$$\begin{align}{J}\!\left(x,y\right) &= \left[\left(\frac{1}{4}-\frac{1}{2 x^2}\right){\rm Re}{\,Z\left(\frac{1}{x}\right)} + \frac{1}{2 x} \right] \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{align}$$(G86c) $$\begin{align}{K}\!\left(x,y\right) &= \frac{\sqrt{\rm \pi}}{2} \left(\frac{1}{x^2}-\frac{1}{2}\right)\exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] . \end{align}$$
$$\begin{align}{K}\!\left(x,y\right) &= \frac{\sqrt{\rm \pi}}{2} \left(\frac{1}{x^2}-\frac{1}{2}\right)\exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] . \end{align}$$(ii)
 $x, y \gg 1$
(G87a)
$x, y \gg 1$
(G87a) $$\begin{align} {I}\!\left(x,y\right) &={-}\frac{\sqrt{\rm \pi} x^3}{4 \left(x^2+y^2\right)^{3/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G87b)
$$\begin{align} {I}\!\left(x,y\right) &={-}\frac{\sqrt{\rm \pi} x^3}{4 \left(x^2+y^2\right)^{3/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G87b) $$\begin{align}{J}\!\left(x,y\right) &={-}\frac{x^3}{\left(x^2+y^2\right)^{2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G87c)
$$\begin{align}{J}\!\left(x,y\right) &={-}\frac{x^3}{\left(x^2+y^2\right)^{2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G87c) $$\begin{align}{K}\!\left(x,y\right) &={-}\frac{\sqrt{\rm \pi} x}{4 \left(x^2+y^2\right)^{1/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] . \end{align}$$
$$\begin{align}{K}\!\left(x,y\right) &={-}\frac{\sqrt{\rm \pi} x}{4 \left(x^2+y^2\right)^{1/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] . \end{align}$$(iii)
 $x \ll 1, y \sim 1$
(G88a)
$x \ll 1, y \sim 1$
(G88a) \begin{align} {I}\!\left(x,y\right) &= \frac{2 \sqrt{\rm \pi}}{x^2 y^2} \exp{\left(-\frac{y^2}{2}-\frac{1 }{x^2}\right)} {I}_1\!\left(\frac{y^2}{2}\right) \left[1+{O}\!\left(x^2\right) \right] , \end{align}(G88b)
\begin{align} {I}\!\left(x,y\right) &= \frac{2 \sqrt{\rm \pi}}{x^2 y^2} \exp{\left(-\frac{y^2}{2}-\frac{1 }{x^2}\right)} {I}_1\!\left(\frac{y^2}{2}\right) \left[1+{O}\!\left(x^2\right) \right] , \end{align}(G88b) \begin{align} {J}\!\left(x,y\right) & ={-}\frac{x}{2} \exp{\left(-\frac{y^2}{2}\right)} \nonumber\\ & \quad \times \left[y^2\left({I}_0\!\left(\frac{y^2}{2}\right)-{I}_1\!\left(\frac{y^2}{2}\right)\right) - {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}(G88c)
\begin{align} {J}\!\left(x,y\right) & ={-}\frac{x}{2} \exp{\left(-\frac{y^2}{2}\right)} \nonumber\\ & \quad \times \left[y^2\left({I}_0\!\left(\frac{y^2}{2}\right)-{I}_1\!\left(\frac{y^2}{2}\right)\right) - {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}(G88c) \begin{align} {K}\!\left(x,y\right) & = \frac{\sqrt{\rm \pi}}{2} \exp{\left(-\frac{y^2}{2}\right)} \left[\left(\frac{1}{2}y^2 -y^4 \right) {I}_0\!\left(\frac{y^2}{2}\right)\right. \nonumber\\ & \quad \left.+\,\left(\frac{1}{2}y^2 +y^4 \right) {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] . \end{align}
\begin{align} {K}\!\left(x,y\right) & = \frac{\sqrt{\rm \pi}}{2} \exp{\left(-\frac{y^2}{2}\right)} \left[\left(\frac{1}{2}y^2 -y^4 \right) {I}_0\!\left(\frac{y^2}{2}\right)\right. \nonumber\\ & \quad \left.+\,\left(\frac{1}{2}y^2 +y^4 \right) {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] . \end{align}(iv)
 $x, y \ll 1$
(G89a)
$x, y \ll 1$
(G89a) $$\begin{align} {I}\!\left(x,y\right) &= \frac{\sqrt{\rm \pi}}{2 x^2} \exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\exp{\left(-\frac{3}{x^2}\right)},y^2 \right) \right] , \end{align}$$(G89b)
$$\begin{align} {I}\!\left(x,y\right) &= \frac{\sqrt{\rm \pi}}{2 x^2} \exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\exp{\left(-\frac{3}{x^2}\right)},y^2 \right) \right] , \end{align}$$(G89b) $$\begin{align}{J}\!\left(x,y\right) &={-}x \left(\frac{3}{8}y^2 - \frac{1}{4} x^2 \right) \left[1+{O}\!\left(x^4, x^2 y^2, y^4\right) \right] , \end{align}$$(G89c)
$$\begin{align}{J}\!\left(x,y\right) &={-}x \left(\frac{3}{8}y^2 - \frac{1}{4} x^2 \right) \left[1+{O}\!\left(x^4, x^2 y^2, y^4\right) \right] , \end{align}$$(G89c) $$\begin{align}{K}\!\left(x,y\right) &= \frac{\sqrt{\rm \pi}}{4} y^2 \left[1+{O}\!\left(x^2, y^2\right) \right] . \end{align}$$
$$\begin{align}{K}\!\left(x,y\right) &= \frac{\sqrt{\rm \pi}}{4} y^2 \left[1+{O}\!\left(x^2, y^2\right) \right] . \end{align}$$
G.4. The CE shear terms
For a CE shear term of the form
we have
This gives
 \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xx} & = \frac{6}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xx} & = \frac{6}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2}\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} }\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xy} & = \frac{6 \mathrm{i}}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} } \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xy} & = \frac{6 \mathrm{i}}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s} \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} } \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xz} & = \frac{6}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xz} & = \frac{6}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \end{align} \begin{align} & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}} \right] , \end{align}
\begin{align} & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\frac{n}{k_{\bot} \tilde{\rho}_s}\int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}} \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{yy} & = \frac{6}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^3 {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}} \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{yy} & = \frac{6}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^3 {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\tilde{v}_{s\|} \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}} \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{yz} & ={-}\frac{6 \mathrm{i}}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{ \int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{yz} & ={-}\frac{6 \mathrm{i}}{\sqrt{\rm \pi}} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot}^2 {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) {J}_n'(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot}) \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{ \int_{C_L} \frac{\tilde{v}_{s\|}^2 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{zz} & = \frac{6}{\sqrt{\rm \pi}} \epsilon_s \left\{ \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}^3 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right.\right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\tilde{v}_{s\|}^3 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] \nonumber\\ & \quad \left.-\, \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|}^2 \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \vphantom{\sum_{n={-}\infty}^{\infty}} \right\} . \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{zz} & = \frac{6}{\sqrt{\rm \pi}} \epsilon_s \left\{ \sum_{n={-}\infty}^{\infty} \left[ \int_{C_L} \frac{\tilde{v}_{s\|}^3 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}} \right.\right. \nonumber\\ & \left. \quad \times \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \, \tilde{v}_{s\bot} {J}_n(k_{\bot} \tilde{\rho}_s \tilde{v}_{s\bot})^2 \exp \left(-\tilde{v}_{s\bot}^2\right) \vphantom{\int_{C_L} \frac{\tilde{v}_{s\|}^3 \exp \left(-\tilde{v}_{s\|}^2\right) \mathrm{d} \tilde{v}_{s\|}}{\tilde{v}_{s\|}-\zeta_{sn}}}\right] \nonumber\\ & \quad \left.-\, \int_{-\infty}^{\infty} \mathrm{d} \tilde{v}_{s\|} \, \tilde{v}_{s\|}^2 \int_0^{\infty} \mathrm{d} \tilde{v}_{s\bot} \,\tilde{v}_{s\bot} \exp \left(-\tilde{v}_{s}^2\right) \vphantom{\sum_{n={-}\infty}^{\infty}} \right\} . \end{align}Again using the Bessel-function identities (G16), and the identities (G15) and (G79a) applicable to the plasma dispersion function, the dielectric tensor's elements become
 \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xx} &= 3\epsilon_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xx} &= 3\epsilon_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xy} & = \frac{3 \mathrm{i}\epsilon_s}{2} \sum_{n={-}\infty}^{\infty} n \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xy} & = \frac{3 \mathrm{i}\epsilon_s}{2} \sum_{n={-}\infty}^{\infty} n \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{xz} &= 3 \epsilon_s \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \zeta_{sn} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{xz} &= 3 \epsilon_s \sum_{n={-}\infty}^{\infty} \frac{n}{k_{\bot} \tilde{\rho}_s} \zeta_{sn} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{yy} & = \frac{3}{2} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ 1+ \zeta_{sn} Z\!\left(\zeta_{sn}\right) \right] \nonumber\\ &\quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{yy} & = \frac{3}{2} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[ 1+ \zeta_{sn} Z\!\left(\zeta_{sn}\right) \right] \nonumber\\ &\quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s)_{yz} & ={-}\frac{3 \mathrm{i}\epsilon_s }{2} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \zeta_{sn} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s)_{yz} & ={-}\frac{3 \mathrm{i}\epsilon_s }{2} \sum_{n={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \zeta_{sn} \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} $$\begin{align}(\boldsymbol{\mathsf{P}}_s)_{zz} &= 3 \epsilon_s \sum_{n={-}\infty}^{\infty} \zeta_{sn}^2 \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{P}}_s)_{zz} &= 3 \epsilon_s \sum_{n={-}\infty}^{\infty} \zeta_{sn}^2 \left[1+\zeta_{sn} Z\!\left(\zeta_{sn}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align}$$G.4.1. Dielectric tensor in low-frequency limit
As with the CE temperature-gradient term, under the ordering ![]() $k_{\|} \rho _s \sim k_{\bot } \rho _s \sim 1$, the expressions (G81) can be approximated by the leading-order term of the expansion of
$k_{\|} \rho _s \sim k_{\bot } \rho _s \sim 1$, the expressions (G81) can be approximated by the leading-order term of the expansion of ![]() $\boldsymbol{\mathsf{P}}_s$ in the low-frequency limit
$\boldsymbol{\mathsf{P}}_s$ in the low-frequency limit ![]() $\tilde {\omega }_{s\|} \ll 1$. Namely, we have
$\tilde {\omega }_{s\|} \ll 1$. Namely, we have
where
 \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xx} & = 3 \epsilon_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xx} & = 3 \epsilon_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot}^2 \tilde{\rho}_s^2} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xy} & = \frac{3 \mathrm{i} \epsilon_s }{2} \sum_{n={-}\infty}^{\infty} n \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xy} & = \frac{3 \mathrm{i} \epsilon_s }{2} \sum_{n={-}\infty}^{\infty} n \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xz} & ={-}3 \epsilon_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot} |k_{\|}| \tilde{\rho}_s^2} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s}Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xz} & ={-}3 \epsilon_s \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\bot} |k_{\|}| \tilde{\rho}_s^2} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s}Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yy} & = \frac{3}{2} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] \nonumber\\ &\quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yy} & = \frac{3}{2} \epsilon_s \sum_{n={-}\infty}^{\infty} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] \nonumber\\ &\quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[\left( \frac{2 n^2}{k_{\bot}^2 \tilde{\rho}_s^2}+k_{\bot}^2 \tilde{\rho}_s^2\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - k_{\bot}^2 \tilde{\rho}_s^2 {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yz} & = \frac{3 \mathrm{i} \epsilon_s}{2} \sum_{n={-}\infty}^{\infty} \frac{n k_{\bot}}{|k_{\|}|} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yz} & = \frac{3 \mathrm{i} \epsilon_s}{2} \sum_{n={-}\infty}^{\infty} \frac{n k_{\bot}}{|k_{\|}|} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] , \end{align} \begin{align}(\boldsymbol{\mathsf{P}}_s^{(0)})_{zz} &= 3 \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align}
\begin{align}(\boldsymbol{\mathsf{P}}_s^{(0)})_{zz} &= 3 \sum_{n={-}\infty}^{\infty} \frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2} \left[1-\frac{n}{|k_{\|}| \tilde{\rho}_s} Z\!\left(-\frac{n}{|k_{\|}| \tilde{\rho}_s}\right)\right] \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) . \end{align}
In this calculation, we have utilised the approximation ![]() $\zeta _{sn} \approx - n/|k_{\|}| \tilde {\rho }_s$. Similarly to the Maxwellian case, we can use the Bessel-function-summation identities (G24) and the symmetry properties of the plasma dispersion function with a real argument to show that
$\zeta _{sn} \approx - n/|k_{\|}| \tilde {\rho }_s$. Similarly to the Maxwellian case, we can use the Bessel-function-summation identities (G24) and the symmetry properties of the plasma dispersion function with a real argument to show that
 \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xx} & = 3 \epsilon_s \left\{ \frac{1}{2} + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{n^3}{|k_{\|}| k_{\bot}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ & = \epsilon_s W(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xx} & = 3 \epsilon_s \left\{ \frac{1}{2} + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{n^3}{|k_{\|}| k_{\bot}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ & = \epsilon_s W(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xy} & = 3 \sqrt{\rm \pi} \epsilon_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & \quad \times \sum_{n=1}^{\infty}\frac{n^2}{|k_{\|}| \tilde{\rho}_s} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\epsilon_s X(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xy} & = 3 \sqrt{\rm \pi} \epsilon_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & \quad \times \sum_{n=1}^{\infty}\frac{n^2}{|k_{\|}| \tilde{\rho}_s} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\epsilon_s X(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xz} & ={-}3 \epsilon_s \left\{ \vphantom{\sum_{n={-}\infty}^{\infty} \frac{n^3}{k_{\bot} k_{\|}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)} \frac{k_{\bot}}{2 |k_{\|}|} + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \left. \times\, \sum_{n={-}\infty}^{\infty} \frac{n^3}{k_{\bot} k_{\|}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ & ={-}\frac{k_{\bot}}{|k_{\|}|} \epsilon_s W(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{xz} & ={-}3 \epsilon_s \left\{ \vphantom{\sum_{n={-}\infty}^{\infty} \frac{n^3}{k_{\bot} k_{\|}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)} \frac{k_{\bot}}{2 |k_{\|}|} + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)\right. \nonumber\\ & \quad \left. \times\, \sum_{n={-}\infty}^{\infty} \frac{n^3}{k_{\bot} k_{\|}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ & ={-}\frac{k_{\bot}}{|k_{\|}|} \epsilon_s W(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yy} & = \frac{3}{2} \epsilon_s \left\{ 1 + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{2 n^3}{|k_{\|}| k_{\bot}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right. \nonumber\\ & \quad + k_{\bot}^2 \tilde{\rho}_s^2 \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{n}{|k_{\|}| \tilde{\rho}_s} \nonumber\\ & \quad \left.\times\, {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } \left[ {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \vphantom{1 + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{2 n^3}{|k_{\|}| k_{\bot}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) } \right\} , \nonumber\\ & = \epsilon_s {Y}(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yy} & = \frac{3}{2} \epsilon_s \left\{ 1 + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{2 n^3}{|k_{\|}| k_{\bot}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right. \nonumber\\ & \quad + k_{\bot}^2 \tilde{\rho}_s^2 \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{n}{|k_{\|}| \tilde{\rho}_s} \nonumber\\ & \quad \left.\times\, {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } \left[ {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) - {I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \vphantom{1 + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{2 n^3}{|k_{\|}| k_{\bot}^2 \tilde{\rho}_s^3} {\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) } \right\} , \nonumber\\ & = \epsilon_s {Y}(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yz} & = 3 \sqrt{\rm \pi} \epsilon_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & \quad \times \sum_{n=1}^{\infty}\frac{k_{\bot} n^2}{k_{\|}^2 \tilde{\rho}_s} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\frac{k_{\bot}}{|k_{\|}|} \epsilon_s X(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{yz} & = 3 \sqrt{\rm \pi} \epsilon_s \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \nonumber\\ & \quad \times \sum_{n=1}^{\infty}\frac{k_{\bot} n^2}{k_{\|}^2 \tilde{\rho}_s} \exp{\left(-\frac{n^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \left[{I}_n'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\frac{k_{\bot}}{|k_{\|}|} \epsilon_s X(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align} \begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{zz} & = 3 \epsilon_s \left\{ \frac{k_{\bot}^2}{2 k_{\|}^2} + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{n^3}{|k_{\|}|^3 \tilde{\rho}_s^3}{\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ & = \frac{k_{\bot}^2}{k_{\|}^2} \epsilon_s W(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align}
\begin{align} (\boldsymbol{\mathsf{P}}_s^{(0)})_{zz} & = 3 \epsilon_s \left\{ \frac{k_{\bot}^2}{2 k_{\|}^2} + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \sum_{n={-}\infty}^{\infty} \frac{n^3}{|k_{\|}|^3 \tilde{\rho}_s^3}{\rm Re}{\left[ Z\!\left(\frac{n}{|k_{\|}| \tilde{\rho}_s}\right) \right] } {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right\} \nonumber\\ & = \frac{k_{\bot}^2}{k_{\|}^2} \epsilon_s W(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s) , \end{align}
where the functions ![]() $W(x,y)$,
$W(x,y)$, ![]() ${Y}(x,y)$ and
${Y}(x,y)$ and ![]() $X(x,y)$ are defined by
$X(x,y)$ are defined by
 $$\begin{align} W\!\left(x,y\right) &\equiv \frac{3}{2} + \frac{3}{xy^2} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} m^3 \, {\rm Re}{\,Z\!\left(\frac{m}{x}\right)} {I}_m\!\left(\frac{y^2}{2}\right) , \end{align}$$
$$\begin{align} W\!\left(x,y\right) &\equiv \frac{3}{2} + \frac{3}{xy^2} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m ={-}\infty}^{\infty} m^3 \, {\rm Re}{\,Z\!\left(\frac{m}{x}\right)} {I}_m\!\left(\frac{y^2}{2}\right) , \end{align}$$ $$\begin{align}X\!\left(x,y\right) &\equiv \frac{3 \sqrt{\rm \pi}}{x} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m=1}^{\infty} m^2 \left[ {I}_m\!\left(\frac{y^2}{2}\right)- {I}_m'\!\left(\frac{y^2}{2}\right)\right] \exp{\left(-\frac{m^2}{x^2}\right)} , \end{align}$$
$$\begin{align}X\!\left(x,y\right) &\equiv \frac{3 \sqrt{\rm \pi}}{x} \exp{\left(-\frac{y^2}{2}\right)} \sum_{m=1}^{\infty} m^2 \left[ {I}_m\!\left(\frac{y^2}{2}\right)- {I}_m'\!\left(\frac{y^2}{2}\right)\right] \exp{\left(-\frac{m^2}{x^2}\right)} , \end{align}$$G.4.2. Asymptotic limits of  $\boldsymbol{\mathsf{P}}_s^{\,(0)}$
$\boldsymbol{\mathsf{P}}_s^{\,(0)}$
As we have done for the other special functions defined in this paper, in this appendix we provide asymptotic expressions in the limits where ![]() $x$ and
$x$ and ![]() $y$ are very small or large for the special functions
$y$ are very small or large for the special functions ![]() $W(x,y)$,
$W(x,y)$, ![]() $X(x,y)$ and
$X(x,y)$ and ![]() ${Y}(x,y)$ defined in (G97). These limits again correspond to parallel and perpendicular wavenumbers that are very small or very large with respect to the inverse Larmor radius of species
${Y}(x,y)$ defined in (G97). These limits again correspond to parallel and perpendicular wavenumbers that are very small or very large with respect to the inverse Larmor radius of species ![]() $s$.
$s$.
Considering various asymptotic limits in a systematic fashion, we find
(i)
 $x \sim 1$,
$x \sim 1$,  $y \ll 1$
(G98a)
$y \ll 1$
(G98a) $$\begin{gather} W\!\left(x,y\right) = \left[\frac{3}{2} +\frac{3}{2 x} {\rm Re}{\,Z\left(\frac{1}{x}\right)} \right] \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{gather}$$(G98b)
$$\begin{gather} W\!\left(x,y\right) = \left[\frac{3}{2} +\frac{3}{2 x} {\rm Re}{\,Z\left(\frac{1}{x}\right)} \right] \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{gather}$$(G98b) $$\begin{gather}X\!\left(x,y\right) ={-}\frac{3 \sqrt{\rm \pi}}{2 x} \exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{gather}$$(G98c)
$$\begin{gather}X\!\left(x,y\right) ={-}\frac{3 \sqrt{\rm \pi}}{2 x} \exp{\left(-\frac{1}{x^2}\right)} \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] , \end{gather}$$(G98c) $$\begin{gather}Y\!\left(x,y\right) = \left[\frac{3}{2} +\frac{3}{2 x} {\rm Re}{\,Z\left(\frac{1}{x}\right)} \right] \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] . \end{gather}$$
$$\begin{gather}Y\!\left(x,y\right) = \left[\frac{3}{2} +\frac{3}{2 x} {\rm Re}{\,Z\left(\frac{1}{x}\right)} \right] \left[1+{O}\!\left(\kern0.7pt y^2\right) \right] . \end{gather}$$(ii)
 $x, y \gg 1$
(G99a)
$x, y \gg 1$
(G99a) $$\begin{align} W\!\left(x,y\right) &= \frac{3 x^2 \left(x^2-y^2\right)}{2 \left(x^2+y^2\right)^2} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G99b)
$$\begin{align} W\!\left(x,y\right) &= \frac{3 x^2 \left(x^2-y^2\right)}{2 \left(x^2+y^2\right)^2} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G99b) $$\begin{align}X\!\left(x,y\right) &= \frac{3 \sqrt{\rm \pi} x^2 \left(\kern0.7pt y^2-2 x^2\right)}{4 \left(x^2+y^2\right)^{5/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G99c)
$$\begin{align}X\!\left(x,y\right) &= \frac{3 \sqrt{\rm \pi} x^2 \left(\kern0.7pt y^2-2 x^2\right)}{4 \left(x^2+y^2\right)^{5/2}} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] , \end{align}$$(G99c) $$\begin{align}Y\!\left(x,y\right) &= \frac{3 x^2}{2\left(x^2 + y^2\right)} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] . \end{align}$$
$$\begin{align}Y\!\left(x,y\right) &= \frac{3 x^2}{2\left(x^2 + y^2\right)} \left[1+{O}\!\left(\frac{1}{x^2+y^2}\right) \right] . \end{align}$$(iii)
 $x \ll 1$,
$x \ll 1$,  $y \sim 1$
(G100a)
$y \sim 1$
(G100a) \begin{align} W\!\left(x,y\right) &={-}\frac{3 x^2}{2 y^2} \left[1-\exp \left(-\frac{y^2}{2}\right) {I}_0\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}(G100b)
\begin{align} W\!\left(x,y\right) &={-}\frac{3 x^2}{2 y^2} \left[1-\exp \left(-\frac{y^2}{2}\right) {I}_0\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] , \end{align}(G100b) \begin{align} X\!\left(x,y\right) & = \frac{3 \sqrt{\rm \pi}}{x} \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)-{I}_1\!\left(\frac{y^2}{2}\right)\right] \nonumber\\ & \quad \times \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)} \right] \right\} , \end{align}(G100c)
\begin{align} X\!\left(x,y\right) & = \frac{3 \sqrt{\rm \pi}}{x} \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)-{I}_1\!\left(\frac{y^2}{2}\right)\right] \nonumber\\ & \quad \times \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)} \right] \right\} , \end{align}(G100c) \begin{align} Y\!\left(x,y\right) &= \frac{3}{2} y^2 \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)- {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] . \end{align}
\begin{align} Y\!\left(x,y\right) &= \frac{3}{2} y^2 \exp{\left(-\frac{y^2}{2}\right)} \left[{I}_0\!\left(\frac{y^2}{2}\right)- {I}_1\!\left(\frac{y^2}{2}\right)\right] \left[1+{O}\!\left(x^2\right) \right] . \end{align}(iv)
 $x, y \ll 1$
(G101a)
$x, y \ll 1$
(G101a) $$\begin{align} W\!\left(x,y\right) &={-}\tfrac{3}{4}x^2 \left[1+{O}\!\left(x^2,y^2 \right) \right] , \end{align}$$(G101b)
$$\begin{align} W\!\left(x,y\right) &={-}\tfrac{3}{4}x^2 \left[1+{O}\!\left(x^2,y^2 \right) \right] , \end{align}$$(G101b) $$\begin{align}X\!\left(x,y\right) &= \frac{3 \sqrt{\rm \pi}}{x} \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\! \left[\exp{\left(-\frac{3}{x^2}\right)},y^2 \right] \right\} , \end{align}$$(G101c)
$$\begin{align}X\!\left(x,y\right) &= \frac{3 \sqrt{\rm \pi}}{x} \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\! \left[\exp{\left(-\frac{3}{x^2}\right)},y^2 \right] \right\} , \end{align}$$(G101c) \begin{align} Y\!\left(x,y\right) & = \left[\tfrac{3}{2} y^2 -\tfrac{3}{4} x^2 - \tfrac{9}{8}\left(x^4- \tfrac{2}{3} x^2 y^2 + y^4\right) \right] \nonumber\\ & \quad \times \left[1+{O}\!\left(x^6, x^4 y^2, x^2 y^4, y^6 \right) \right] . \end{align}
\begin{align} Y\!\left(x,y\right) & = \left[\tfrac{3}{2} y^2 -\tfrac{3}{4} x^2 - \tfrac{9}{8}\left(x^4- \tfrac{2}{3} x^2 y^2 + y^4\right) \right] \nonumber\\ & \quad \times \left[1+{O}\!\left(x^6, x^4 y^2, x^2 y^4, y^6 \right) \right] . \end{align}(v)
 $x \ll 1$,
$x \ll 1$,  $y \gg 1$
(G102a)
$y \gg 1$
(G102a) $$\begin{align} W\!\left(x,y\right) &={-}\frac{3 x^2}{2 y^2} \left[1+{O}\!\left(x^2,\frac{1}{y^2}\right) \right] , \end{align}$$(G102b)
$$\begin{align} W\!\left(x,y\right) &={-}\frac{3 x^2}{2 y^2} \left[1+{O}\!\left(x^2,\frac{1}{y^2}\right) \right] , \end{align}$$(G102b) $$\begin{align}X\!\left(x,y\right) &= \frac{3}{x y^3} \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)},\frac{1}{y^2} \right] \right\} , \end{align}$$(G102c)
$$\begin{align}X\!\left(x,y\right) &= \frac{3}{x y^3} \exp{\left(-\frac{1}{x^2}\right)} \left\{1+{O}\!\left[\exp{\left(-\frac{3}{x^2}\right)},\frac{1}{y^2} \right] \right\} , \end{align}$$(G102c) $$\begin{align}Y\!\left(x,y\right) &= \frac{3}{2 \sqrt{\rm \pi} y} \left[1+{O}\!\left(x^2,\frac{1}{y^2}\right) \right] . \end{align}$$
$$\begin{align}Y\!\left(x,y\right) &= \frac{3}{2 \sqrt{\rm \pi} y} \left[1+{O}\!\left(x^2,\frac{1}{y^2}\right) \right] . \end{align}$$
Appendix H. Density perturbations for low-frequency modes
In this appendix, we derive an expression for the (Fourier-transformed) perturbation of number density ![]() $\hat {\delta n}_s$ of species
$\hat {\delta n}_s$ of species ![]() $s$ associated with a low-frequency mode, in terms of the expanded terms of the dielectric tensor
$s$ associated with a low-frequency mode, in terms of the expanded terms of the dielectric tensor ![]() $\boldsymbol {\mathfrak {E}}_s = \tilde {\omega }_{s\|}\boldsymbol {\mathfrak {E}}_s^{(0)} + \tilde {\omega }_{s\|}^2 \boldsymbol {\mathfrak {E}}_s^{(1)} + \ldots$ of species
$\boldsymbol {\mathfrak {E}}_s = \tilde {\omega }_{s\|}\boldsymbol {\mathfrak {E}}_s^{(0)} + \tilde {\omega }_{s\|}^2 \boldsymbol {\mathfrak {E}}_s^{(1)} + \ldots$ of species ![]() $s$ and the perturbed electric field,
$s$ and the perturbed electric field, ![]() $\widehat {\delta \boldsymbol {E}}$; we will show that
$\widehat {\delta \boldsymbol {E}}$; we will show that ![]() $\hat {\delta n}_s$ is, in fact, independent of
$\hat {\delta n}_s$ is, in fact, independent of ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$. We then derive an expression for the perturbed density of all sub-ion-Larmor scale (
$\boldsymbol {\mathfrak {E}}_s^{(0)}$. We then derive an expression for the perturbed density of all sub-ion-Larmor scale (![]() $k \rho _i \gg 1$), low-frequency modes.
$k \rho _i \gg 1$), low-frequency modes.
H.1. Derivation of general expressions
We begin with the continuity equation (2.4a), which describes the time evolution of the density of species ![]() $s$ in terms of itself and the bulk velocity of the same species. For any small-scale, small-amplitude perturbed density
$s$ in terms of itself and the bulk velocity of the same species. For any small-scale, small-amplitude perturbed density ![]() $\delta n_s$ and bulk velocity
$\delta n_s$ and bulk velocity ![]() $\delta \boldsymbol {V}_s$ of some (much more slowly evolving, much larger-scale) quasi-equilibrium state with mean density
$\delta \boldsymbol {V}_s$ of some (much more slowly evolving, much larger-scale) quasi-equilibrium state with mean density ![]() $n_{s0} \gg \delta n_s$ and bulk velocity
$n_{s0} \gg \delta n_s$ and bulk velocity ![]() $\boldsymbol {V}_{s0} \gg \delta \boldsymbol {V}_s$, viz.
$\boldsymbol {V}_{s0} \gg \delta \boldsymbol {V}_s$, viz.
the continuity equation governing that perturbation is
where we have neglected all terms that are quadratic in the perturbation amplitude, and also the terms that are proportional to gradients of the equilibrium state, which by assumption are much smaller than the remaining terms. Assuming the perturbation has the form
we deduce from (H2) that
The perturbed velocity ![]() $\widehat {\delta \boldsymbol {V}}_s$ can be written in terms of the dielectric tensor of species
$\widehat {\delta \boldsymbol {V}}_s$ can be written in terms of the dielectric tensor of species ![]() $s$ using Ohm's law (C13) and (2.96):
$s$ using Ohm's law (C13) and (2.96):
whence, by way of (H4),
Finally, we note that the symmetries (2.102) of ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$ imply that it does not contribute to the right-hand side of (H6), which implies in turn that
$\boldsymbol {\mathfrak {E}}_s^{(0)}$ imply that it does not contribute to the right-hand side of (H6), which implies in turn that
Thus, for low-frequency modes, ![]() $\widehat {\delta n}_s$ is a function of the electric field and
$\widehat {\delta n}_s$ is a function of the electric field and ![]() $\boldsymbol {\mathfrak {E}}_s^{(1)}$, but not of
$\boldsymbol {\mathfrak {E}}_s^{(1)}$, but not of ![]() $\boldsymbol {\mathfrak {E}}_s^{(0)}$.
$\boldsymbol {\mathfrak {E}}_s^{(0)}$.
We note that the condition (2.109) implies that, for low-frequency modes, quasi-neutrality is maintained:
Thus, in a two-species plasma, the ion number density associated with a perturbation can be calculated if the electron number density is known, and vice versa.
H.2. Special case: sub-ion-Larmor-scale modes in a two-species plasma
In the special case of a two-species plasma whose characteristic parallel wavenumber satisfies ![]() $k_{\|} \rho _i \gg 1$, a particularly simple expression for the perturbed number densities of ions (and electrons) can be derived: the Boltzmann response. This arises because the ion dielectric tensor
$k_{\|} \rho _i \gg 1$, a particularly simple expression for the perturbed number densities of ions (and electrons) can be derived: the Boltzmann response. This arises because the ion dielectric tensor ![]() $\boldsymbol {\mathfrak {E}}_i$ is unmagnetised, and so takes the simple form (valid for arbitrary
$\boldsymbol {\mathfrak {E}}_i$ is unmagnetised, and so takes the simple form (valid for arbitrary ![]() $\tilde {\omega }_i = \omega /k v_{\mathrm {th}i}$) that was derived in Appendix G.1.5:
$\tilde {\omega }_i = \omega /k v_{\mathrm {th}i}$) that was derived in Appendix G.1.5:
It follows that
Now assuming that ![]() $\tilde {\omega }_i \ll 1$, it follows that
$\tilde {\omega }_i \ll 1$, it follows that
Expression (H7) with ![]() $s = i$ then gives
$s = i$ then gives
Finally, introducing the electrostatic potential ![]() $\varphi$, whose Fourier transform is related to the electrostatic component of the electric field via
$\varphi$, whose Fourier transform is related to the electrostatic component of the electric field via
we deduce that
and
where we have used the quasi-neutrality relation ![]() $n_{e0} = Z_i n_{i0}$ for the equilibrium state.
$n_{e0} = Z_i n_{i0}$ for the equilibrium state.
Appendix I. Calculating the electrostatic field from the transverse electric field
In Appendix G.1.3, it was shown that, for any distribution function with a small anisotropy,
which implies that the leading-order terms (in ![]() $\tilde {\omega }_{s\|} \ll 1$) of the dielectric tensor are insufficient to determine the electrostatic field. To do this, we must go to the next order in
$\tilde {\omega }_{s\|} \ll 1$) of the dielectric tensor are insufficient to determine the electrostatic field. To do this, we must go to the next order in ![]() $\tilde {\omega }_{s\|} \ll 1$. To illustrate how such a calculation is done, in this appendix, we derive an expression for the electrostatic field component
$\tilde {\omega }_{s\|} \ll 1$. To illustrate how such a calculation is done, in this appendix, we derive an expression for the electrostatic field component ![]() $\hat {\boldsymbol {k}} \boldsymbol {\cdot } \widehat {\delta \boldsymbol {E}}$ in terms of the transverse electric field
$\hat {\boldsymbol {k}} \boldsymbol {\cdot } \widehat {\delta \boldsymbol {E}}$ in terms of the transverse electric field ![]() $\widehat {\delta \boldsymbol {E}}_{T}$ and special functions when the underlying particle distribution function is Maxwellian.
$\widehat {\delta \boldsymbol {E}}_{T}$ and special functions when the underlying particle distribution function is Maxwellian.
To achieve this aim, we first derive a relation between the components of the electric field in the coordinate basis ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$. We begin with the consistency condition (2.110) appropriate for non-relativistic electromagnetic fluctuations
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$. We begin with the consistency condition (2.110) appropriate for non-relativistic electromagnetic fluctuations
Writing ![]() $\hat {\boldsymbol {k}}$,
$\hat {\boldsymbol {k}}$, ![]() $\boldsymbol {\mathfrak {E}}$ and
$\boldsymbol {\mathfrak {E}}$ and ![]() $\widehat {\delta \boldsymbol {E}}$ in the basis
$\widehat {\delta \boldsymbol {E}}$ in the basis ![]() $\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$, this becomes
$\{\hat {\boldsymbol {x}},\hat {\boldsymbol {y}},\hat {\boldsymbol {z}}\}$, this becomes
Now considering the case of fluctuations that satisfy ![]() $\tilde {\omega }_{s\|} \ll 1$ for all particle species
$\tilde {\omega }_{s\|} \ll 1$ for all particle species ![]() $s$, and expanding the components of the dielectric in
$s$, and expanding the components of the dielectric in ![]() $\tilde {\omega }_{s\|} \ll 1$, we find
$\tilde {\omega }_{s\|} \ll 1$, we find
where
From (G26), we have
 \begin{align} k_{\bot} \mathfrak{E}_{xx}^{(1)} + k_{\|} \mathfrak{E}_{xz}^{(1)} & ={-} \sum_s \frac{2 k_{\|} \omega_{{\rm p}s}^2 \tilde{\omega}_{s\|}^2}{\omega^2} \sum_{m={-}\infty}^{\infty} \frac{m}{k_{\bot} \tilde{\rho}_s}{\rm Re}{\,Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align}
\begin{align} k_{\bot} \mathfrak{E}_{xx}^{(1)} + k_{\|} \mathfrak{E}_{xz}^{(1)} & ={-} \sum_s \frac{2 k_{\|} \omega_{{\rm p}s}^2 \tilde{\omega}_{s\|}^2}{\omega^2} \sum_{m={-}\infty}^{\infty} \frac{m}{k_{\bot} \tilde{\rho}_s}{\rm Re}{\,Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) , \end{align} \begin{align} k_{\bot} \mathfrak{E}_{xy}^{(1)} - k_{\|} \mathfrak{E}_{yz}^{(1)} & = \sum_s \frac{\sqrt{\rm \pi} k_{\|} \omega_{{\rm p}s}^2 \tilde{\omega}_{s\|}^2}{\omega^2} \sum_{m={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\! \left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right], \end{align}
\begin{align} k_{\bot} \mathfrak{E}_{xy}^{(1)} - k_{\|} \mathfrak{E}_{yz}^{(1)} & = \sum_s \frac{\sqrt{\rm \pi} k_{\|} \omega_{{\rm p}s}^2 \tilde{\omega}_{s\|}^2}{\omega^2} \sum_{m={-}\infty}^{\infty} k_{\bot} \tilde{\rho}_s \exp{\left(-\frac{m^2}{k_{\|}^2 \tilde{\rho}_s^2}\right)} \nonumber\\ & \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \left[{I}_m'\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right)-{I}_m\! \left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right], \end{align} \begin{align} k_{\bot} \mathfrak{E}_{xz}^{(1)} + k_{\|} \mathfrak{E}_{zz}^{(1)} & = \sum_s \frac{2 k_{\|} \omega_{{\rm p}s}^2 \tilde{\omega}_{s\|}^2}{\omega^2} \left[1 + \sum_{m={-}\infty}^{\infty} \frac{m}{|k_{\|}| \tilde{\rho}_s} {\rm Re}{\,Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)} \right. \nonumber\\ & \left. \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \vphantom{\sum_{m={-}\infty}^{\infty} \frac{m}{|k_{\|}| \tilde{\rho}_s} {\rm Re}{\,Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)}} \right] . \end{align}
\begin{align} k_{\bot} \mathfrak{E}_{xz}^{(1)} + k_{\|} \mathfrak{E}_{zz}^{(1)} & = \sum_s \frac{2 k_{\|} \omega_{{\rm p}s}^2 \tilde{\omega}_{s\|}^2}{\omega^2} \left[1 + \sum_{m={-}\infty}^{\infty} \frac{m}{|k_{\|}| \tilde{\rho}_s} {\rm Re}{\,Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)} \right. \nonumber\\ & \left. \quad \times \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_m\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \vphantom{\sum_{m={-}\infty}^{\infty} \frac{m}{|k_{\|}| \tilde{\rho}_s} {\rm Re}{\,Z\left(\frac{m}{|k_{\|}| \tilde{\rho}_s}\right)}} \right] . \end{align}
Thus, we have the following relationship between ![]() $\widehat {\delta E}_{x}$,
$\widehat {\delta E}_{x}$, ![]() $\widehat {\delta E}_{y}$ and
$\widehat {\delta E}_{y}$ and ![]() $\widehat {\delta E}_{z}$:
$\widehat {\delta E}_{z}$:
 \begin{align} &\sum_s \frac{k_{{\rm D}s}^2}{2 k_{\|}^2} \left\{\vphantom{\left[2+\frac{k_{\bot}}{k_{\|}} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right)\right]} -L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) \widehat{\delta E}_{x} + N\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) \widehat{\delta E}_{y}\right. \nonumber\\ &\quad + \left. \left[2+\frac{k_{\bot}}{k_{\|}} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right)\right] \widehat{\delta E}_{z} \right\} = 0 , \end{align}
\begin{align} &\sum_s \frac{k_{{\rm D}s}^2}{2 k_{\|}^2} \left\{\vphantom{\left[2+\frac{k_{\bot}}{k_{\|}} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right)\right]} -L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) \widehat{\delta E}_{x} + N\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) \widehat{\delta E}_{y}\right. \nonumber\\ &\quad + \left. \left[2+\frac{k_{\bot}}{k_{\|}} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right)\right] \widehat{\delta E}_{z} \right\} = 0 , \end{align}
where ![]() $k_{{\rm D}s}$ is the Debye wavenumber (D12), and
$k_{{\rm D}s}$ is the Debye wavenumber (D12), and ![]() $L(x,y)$ and
$L(x,y)$ and ![]() $N(x,y)$ were defined previously by (G32). Using the identities
$N(x,y)$ were defined previously by (G32). Using the identities
we can rearrange (I7) to give
 \begin{align} \frac{1}{k_{\|} k}\left(\sum_s k_{{\rm D}s}^2 \right) \widehat{\delta E}_{3} & = \sum_s \frac{k_{{\rm D}s}^2}{2 k_{\|}^2} \left\{ \left[\frac{k}{k_{\|}} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) + 2 \frac{k_{\bot}}{k} \right] \widehat{\delta E}_{1}\right. \nonumber\\ & \quad \left.-\, N\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) \widehat{\delta E}_{2} \vphantom{\left[\frac{k}{k_{\|}} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) + 2 \frac{k_{\bot}}{k} \right]} \right\} . \end{align}
\begin{align} \frac{1}{k_{\|} k}\left(\sum_s k_{{\rm D}s}^2 \right) \widehat{\delta E}_{3} & = \sum_s \frac{k_{{\rm D}s}^2}{2 k_{\|}^2} \left\{ \left[\frac{k}{k_{\|}} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) + 2 \frac{k_{\bot}}{k} \right] \widehat{\delta E}_{1}\right. \nonumber\\ & \quad \left.-\, N\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) \widehat{\delta E}_{2} \vphantom{\left[\frac{k}{k_{\|}} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) + 2 \frac{k_{\bot}}{k} \right]} \right\} . \end{align}Thus, the electrostatic field is related to the transverse field by
 \begin{align} \hat{\boldsymbol{k}} \boldsymbol{\cdot} \widehat{\delta \boldsymbol{E}} & = \left(\sum_s \frac{Z_s T_e}{T_s} \right)^{{-}1} \sum_s \frac{Z_s T_e}{T_s} \left\{ \left[\frac{k^2}{2 k_{\|}^2} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) + \frac{k_{\bot}}{k_{\|}} \right] \widehat{\delta E}_{1} \right. \nonumber\\ & \quad \left.-\, \frac{k}{2 k_{\|}} N\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) \widehat{\delta E}_{2} \vphantom{\left[\frac{k^2}{2 k_{\|}^2} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) + \frac{k_{\bot}}{k_{\|}} \right] }\right\} . \end{align}
\begin{align} \hat{\boldsymbol{k}} \boldsymbol{\cdot} \widehat{\delta \boldsymbol{E}} & = \left(\sum_s \frac{Z_s T_e}{T_s} \right)^{{-}1} \sum_s \frac{Z_s T_e}{T_s} \left\{ \left[\frac{k^2}{2 k_{\|}^2} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) + \frac{k_{\bot}}{k_{\|}} \right] \widehat{\delta E}_{1} \right. \nonumber\\ & \quad \left.-\, \frac{k}{2 k_{\|}} N\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) \widehat{\delta E}_{2} \vphantom{\left[\frac{k^2}{2 k_{\|}^2} L\!\left(|k_{\|}| \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) + \frac{k_{\bot}}{k_{\|}} \right] }\right\} . \end{align}Appendix J. Methodology for characterising CET microinstabilities
In this appendix, we describe our method for calculating the real frequencies and growth rates of microinstabilities driven by the CE electron- and ion-temperature-gradient, and electron-friction terms when the Krook collision operator is assumed. The method follows that outlined in § 2.5: that is, motivated by the considerations of § 2.3.4, we assume that all significant CET microinstabilities are low frequency (![]() $\omega \ll k_{\|} v_{\mathrm {th}s}$ for at least one particle species), and derive algebraic dispersion relations of such microinstabilities (a particular example of which is given by (2.118)). The growth rate of CET microinstabilities (and, therefore, the stability of the electron and ion CE distribution functions (3.1a) and (3.1b)) as a function of their parallel and perpendicular wavenumbers
$\omega \ll k_{\|} v_{\mathrm {th}s}$ for at least one particle species), and derive algebraic dispersion relations of such microinstabilities (a particular example of which is given by (2.118)). The growth rate of CET microinstabilities (and, therefore, the stability of the electron and ion CE distribution functions (3.1a) and (3.1b)) as a function of their parallel and perpendicular wavenumbers ![]() $k_{\|}$ and
$k_{\|}$ and ![]() $k_{\perp }$ is assessed by solving this dispersion relation for the complex frequency
$k_{\perp }$ is assessed by solving this dispersion relation for the complex frequency ![]() $\omega$, and then evaluating its imaginary part.
$\omega$, and then evaluating its imaginary part.
As we explained in § 2.5, to construct the algebraic, low-frequency dispersion relation for particular forms of CE distribution function for each particle species ![]() $s$, we must evaluate its (leading-order) non-Maxwellian contribution to the dielectric tensor,
$s$, we must evaluate its (leading-order) non-Maxwellian contribution to the dielectric tensor, ![]() $\boldsymbol{\mathsf{P}}_{s} \approx \boldsymbol{\mathsf{P}}_{s}^{(0)}$ (see (2.97) and (G10) for the precise relation of this quantity to the dielectric tensor
$\boldsymbol{\mathsf{P}}_{s} \approx \boldsymbol{\mathsf{P}}_{s}^{(0)}$ (see (2.97) and (G10) for the precise relation of this quantity to the dielectric tensor ![]() $\boldsymbol {\mathfrak {E}}_s$). This is done for the CE electron-friction term in Appendix J.1, and for the CE temperature-gradient terms in Appendix J.2. We then deduce the algebraic dispersion relations of CE electron-temperature-gradient-driven microinstabilities in Appendix J.3, and of CE ion-temperature-gradient-driven microinstabilities in Appendix J.4. Within these two appendices, respectively, we also present derivations of the (further) simplified dispersion relations for the parallel CET whistler instability (Appendix J.3.1), the parallel CET slow-hydromagnetic-wave instability (Appendix J.4.1), and the CET long-wavelength KAW instability (Appendix J.4.2), from which the frequencies and growth rates of these instabilities that are stated in § 3.3 are calculated.
$\boldsymbol {\mathfrak {E}}_s$). This is done for the CE electron-friction term in Appendix J.1, and for the CE temperature-gradient terms in Appendix J.2. We then deduce the algebraic dispersion relations of CE electron-temperature-gradient-driven microinstabilities in Appendix J.3, and of CE ion-temperature-gradient-driven microinstabilities in Appendix J.4. Within these two appendices, respectively, we also present derivations of the (further) simplified dispersion relations for the parallel CET whistler instability (Appendix J.3.1), the parallel CET slow-hydromagnetic-wave instability (Appendix J.4.1), and the CET long-wavelength KAW instability (Appendix J.4.2), from which the frequencies and growth rates of these instabilities that are stated in § 3.3 are calculated.
J.1. Dielectric response of CE electron-friction term
We first consider the CE electron-friction term when evaluating ![]() $\boldsymbol{\mathsf{P}}_{e}^{(0)}$, defined in (2.97). We showed in Appendix G.2 that, when a Krook collision operator was assumed, if
$\boldsymbol{\mathsf{P}}_{e}^{(0)}$, defined in (2.97). We showed in Appendix G.2 that, when a Krook collision operator was assumed, if ![]() $\eta _e^T = \eta _i = 0$, then (see (G74))
$\eta _e^T = \eta _i = 0$, then (see (G74))
It follows that the dispersion relation of all plasma modes is identical to that in a Maxwellian plasma, only with shifted complex frequencies ![]() $\tilde {\omega }_{e\|}^{*} \equiv \tilde {\omega }_{e\|} + \eta _e^R/2$. Since
$\tilde {\omega }_{e\|}^{*} \equiv \tilde {\omega }_{e\|} + \eta _e^R/2$. Since ![]() ${\rm Im}{(\tilde {\omega }_{e\|})} < 0$ for all modes in a Maxwellian plasma, we conclude that
${\rm Im}{(\tilde {\omega }_{e\|})} < 0$ for all modes in a Maxwellian plasma, we conclude that ![]() ${\rm Im}{(\tilde {\omega }_{e\|}^{*})} < 0$ also, and hence the CE electron-friction term cannot drive any microinstabilities when a Krook collision operator is employed: instead, it merely modifies the real frequency of the waves. Thus, when characterising CET microinstabilities, we henceforth ignore the CE electron-friction term, as well as the electron–ion-drift term (viz.
${\rm Im}{(\tilde {\omega }_{e\|}^{*})} < 0$ also, and hence the CE electron-friction term cannot drive any microinstabilities when a Krook collision operator is employed: instead, it merely modifies the real frequency of the waves. Thus, when characterising CET microinstabilities, we henceforth ignore the CE electron-friction term, as well as the electron–ion-drift term (viz. ![]() $\eta _e^R = \eta _e^u = 0$).
$\eta _e^R = \eta _e^u = 0$).
J.2. Dielectric response of CE temperature-gradient terms
Now consider the CE temperature-gradient terms. It is shown in Appendix G.3 that ![]() $\boldsymbol{\mathsf{P}}_{s}^{(0)}$ is given by
$\boldsymbol{\mathsf{P}}_{s}^{(0)}$ is given by
 $$\begin{align} (\boldsymbol{\mathsf{P}}_{e}^{(0)})_{11} &= \mathrm{i} \eta_e^T \frac{k^2}{k_{\|}^2} {I}\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{P}}_{e}^{(0)})_{11} &= \mathrm{i} \eta_e^T \frac{k^2}{k_{\|}^2} {I}\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) , \end{align}$$
where the special functions ![]() ${I}(x,y)$,
${I}(x,y)$, ![]() ${J}(x,y)$ and
${J}(x,y)$ and ![]() ${K}(x,y)$ are defined by (G85). Note that
${K}(x,y)$ are defined by (G85). Note that ![]() $\tilde {\rho }_e < 0$, by definition. The contribution
$\tilde {\rho }_e < 0$, by definition. The contribution ![]() $\boldsymbol{\mathsf{P}}_{i}^{(0)}$ associated with the CE ion-temperature-gradient terms is given by
$\boldsymbol{\mathsf{P}}_{i}^{(0)}$ associated with the CE ion-temperature-gradient terms is given by
 $$\begin{align} (\boldsymbol{\mathsf{P}}_{i}^{(0)})_{11} &= \mathrm{i} \eta_i \frac{k^2}{k_{\|}^2} {I}\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{P}}_{i}^{(0)})_{11} &= \mathrm{i} \eta_i \frac{k^2}{k_{\|}^2} {I}\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) , \end{align}$$J.3. Approximate dispersion relation of CE electron-temperature-gradient-driven microinstabilities
We first consider microinstabilities for which ![]() $\tilde {\omega }_{e\|} = \omega /k_{\|} v_{\mathrm {th}e} \sim \eta _e^T$. It follows that
$\tilde {\omega }_{e\|} = \omega /k_{\|} v_{\mathrm {th}e} \sim \eta _e^T$. It follows that ![]() $\tilde {\omega }_{i\|} = \omega /k_{\|} v_{\mathrm {th}i} \sim \eta _e^T \mu _e^{-1/2} \gg \eta _i$. Therefore, the CE ion-temperature-gradient term is irrelevant for such instabilities, and we need consider only the electron-temperature-gradient term. We also assume that the Maxwellian contribution to the dielectric tensor,
$\tilde {\omega }_{i\|} = \omega /k_{\|} v_{\mathrm {th}i} \sim \eta _e^T \mu _e^{-1/2} \gg \eta _i$. Therefore, the CE ion-temperature-gradient term is irrelevant for such instabilities, and we need consider only the electron-temperature-gradient term. We also assume that the Maxwellian contribution to the dielectric tensor, ![]() $\boldsymbol{\mathsf{M}}_{i}$, can be ignored for such microinstabilities – the validity of this assumption is discussed at the end of this section.
$\boldsymbol{\mathsf{M}}_{i}$, can be ignored for such microinstabilities – the validity of this assumption is discussed at the end of this section.
The dispersion relation for microinstabilities under the ordering ![]() $\tilde {\omega }_{e\|} \sim \eta _e^T \sim 1/\beta _e$ is then given by (2.118), with
$\tilde {\omega }_{e\|} \sim \eta _e^T \sim 1/\beta _e$ is then given by (2.118), with ![]() $\boldsymbol{\mathsf{M}}_{e}^{(0)}$ and
$\boldsymbol{\mathsf{M}}_{e}^{(0)}$ and ![]() $\boldsymbol{\mathsf{P}}_{e}^{(0)}$ substituted for by (2.121) and (J2), respectively,
$\boldsymbol{\mathsf{P}}_{e}^{(0)}$ substituted for by (2.121) and (J2), respectively,
 \begin{align} &\left[\tilde{\omega}_{e\|} F\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) + \eta_e^T {I}\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right)+ \mathrm{i} k_{\|}^2 d_e^2\right] \nonumber\\ &\quad \times \left[\tilde{\omega}_{e\|} H\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) + \eta_e^T {K}\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) +\mathrm{i} k^2 d_e^2\right] \nonumber\\ &\quad + \left[\tilde{\omega}_{e\|} G\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) + \eta_e^T {J}\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right)\right]^2 = 0 . \end{align}
\begin{align} &\left[\tilde{\omega}_{e\|} F\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) + \eta_e^T {I}\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right)+ \mathrm{i} k_{\|}^2 d_e^2\right] \nonumber\\ &\quad \times \left[\tilde{\omega}_{e\|} H\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) + \eta_e^T {K}\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) +\mathrm{i} k^2 d_e^2\right] \nonumber\\ &\quad + \left[\tilde{\omega}_{e\|} G\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right) + \eta_e^T {J}\!\left(k_{\|} \tilde{\rho}_e,k_{\bot} \tilde{\rho}_e\right)\right]^2 = 0 . \end{align}
We remind the reader that we have ordered ![]() $k^2 d_e^2 \sim \eta _e^T$ and
$k^2 d_e^2 \sim \eta _e^T$ and ![]() $k \rho _e \sim 1$. Noting that
$k \rho _e \sim 1$. Noting that ![]() $\beta _e = \rho _e^2/d_e^2$, we can rewrite the skin-depth terms as follows:
$\beta _e = \rho _e^2/d_e^2$, we can rewrite the skin-depth terms as follows:
This allows for the dispersion relation (J4) to be arranged as a quadratic in the complex variable ![]() $\tilde {\omega }_{e\|} \beta _e$:
$\tilde {\omega }_{e\|} \beta _e$:
where
and ![]() $F_e \equiv F(k_{\|} \tilde {\rho }_e,k_{\bot } \tilde {\rho }_e)$,
$F_e \equiv F(k_{\|} \tilde {\rho }_e,k_{\bot } \tilde {\rho }_e)$, ![]() $G_e \equiv G(k_{\|} \tilde {\rho }_e,k_{\bot } \tilde {\rho }_e)$, etc. Solving (J6) gives two roots; restoring dimensions to the complex frequency, they are
$G_e \equiv G(k_{\|} \tilde {\rho }_e,k_{\bot } \tilde {\rho }_e)$, etc. Solving (J6) gives two roots; restoring dimensions to the complex frequency, they are
recovering (3.12). For a given wavenumber, we use (J10) to calculate the growth rates of the perturbations – and, in particular, to see if positive growth rates are present. If they are, it is anticipated that they will have typical size ![]() $\gamma \sim \varOmega _e/\beta _e \sim \eta _e^T \varOmega _e$ (or
$\gamma \sim \varOmega _e/\beta _e \sim \eta _e^T \varOmega _e$ (or ![]() $\tilde {\omega }_{e\|} \sim 1/\beta _e \sim \eta _e^T$).
$\tilde {\omega }_{e\|} \sim 1/\beta _e \sim \eta _e^T$).
When deriving (J10), we assumed that neglecting the Maxwellian ion response was legitimate. It is clear that if ![]() $\tilde {\omega }_{i\|} \gg 1$, then thermal ions are effectively static to electromagnetic perturbations, and so their contribution
$\tilde {\omega }_{i\|} \gg 1$, then thermal ions are effectively static to electromagnetic perturbations, and so their contribution ![]() $\boldsymbol{\mathsf{M}}_{i}$ to the dielectric tensor can be ignored. In terms of a condition on
$\boldsymbol{\mathsf{M}}_{i}$ to the dielectric tensor can be ignored. In terms of a condition on ![]() $\eta _e^{T}$, the scaling
$\eta _e^{T}$, the scaling ![]() $\eta _e^{T} \sim \tilde {\omega }_{e\|}$ gives
$\eta _e^{T} \sim \tilde {\omega }_{e\|}$ gives ![]() $\eta _e^{T} \gg \mu _e^{1/2}$, so this regime is valid for sufficiently large
$\eta _e^{T} \gg \mu _e^{1/2}$, so this regime is valid for sufficiently large ![]() $\eta _e^{T}$. For
$\eta _e^{T}$. For ![]() $\tilde {\omega }_{i\|} \lesssim 1$, it is not immediately clear in the same way that the ion contribution to the dielectric tensor is small. However, having deduced the typical magnitude of the complex frequency of perturbations whilst ignoring ion contributions, we are now able to confirm that our neglect of
$\tilde {\omega }_{i\|} \lesssim 1$, it is not immediately clear in the same way that the ion contribution to the dielectric tensor is small. However, having deduced the typical magnitude of the complex frequency of perturbations whilst ignoring ion contributions, we are now able to confirm that our neglect of ![]() $\boldsymbol{\mathsf{M}}_{i}$ was justified.
$\boldsymbol{\mathsf{M}}_{i}$ was justified.
Since ![]() $k \rho _e \sim 1$ under the ordering assumed when deriving (J4), we conclude that the Maxwellian ion response is unmagnetised:
$k \rho _e \sim 1$ under the ordering assumed when deriving (J4), we conclude that the Maxwellian ion response is unmagnetised: ![]() $k \rho _i \gg 1$. As a consequence, it can be shown (see Appendix G.1.5) that the transverse components of
$k \rho _i \gg 1$. As a consequence, it can be shown (see Appendix G.1.5) that the transverse components of ![]() $\boldsymbol{\mathsf{M}}_{i}$ are given by
$\boldsymbol{\mathsf{M}}_{i}$ are given by
where ![]() $\tilde {\omega }_i \equiv \omega /k v_{\mathrm {th}i} = k_{\|} \tilde {\omega }_{i\|}/k$. Then, estimating the size of the neglected Maxwellian ion contribution to the dielectric tensor (assuming
$\tilde {\omega }_i \equiv \omega /k v_{\mathrm {th}i} = k_{\|} \tilde {\omega }_{i\|}/k$. Then, estimating the size of the neglected Maxwellian ion contribution to the dielectric tensor (assuming ![]() $k_{\|} \sim k$) as compared with the equivalent electron contribution, we find
$k_{\|} \sim k$) as compared with the equivalent electron contribution, we find
where we have used ![]() $\boldsymbol {\mathfrak {E}}_i = \mu _e \boldsymbol{\mathsf{M}}_{i}$ and
$\boldsymbol {\mathfrak {E}}_i = \mu _e \boldsymbol{\mathsf{M}}_{i}$ and ![]() $\boldsymbol {\mathfrak {E}}_e^{(0)} = \tilde {\omega }_{e\|} \boldsymbol{\mathsf{M}}_{e}^{(0)} + \boldsymbol{\mathsf{P}}_{e}^{(0)}$ (see § 2.5.3). Since
$\boldsymbol {\mathfrak {E}}_e^{(0)} = \tilde {\omega }_{e\|} \boldsymbol{\mathsf{M}}_{e}^{(0)} + \boldsymbol{\mathsf{P}}_{e}^{(0)}$ (see § 2.5.3). Since ![]() $|Z(z)| \lesssim 1$ for all
$|Z(z)| \lesssim 1$ for all ![]() $z$ with positive imaginary part (Fried & Conte Reference Fried and Conte1961), we conclude that the ion contribution to the dielectric tensor is indeed small for unstable perturbations, irrespective of the value of
$z$ with positive imaginary part (Fried & Conte Reference Fried and Conte1961), we conclude that the ion contribution to the dielectric tensor is indeed small for unstable perturbations, irrespective of the value of ![]() $\tilde {\omega }_{i\|}$, and so its neglect was valid.
$\tilde {\omega }_{i\|}$, and so its neglect was valid.
J.3.1. Derivation of frequency and growth rate of the parallel CET whistler instability
The dispersion relation of unstable whistler waves with their wavevector parallel to ![]() $\boldsymbol {B}_0$ is obtained by taking the subsidiary limit
$\boldsymbol {B}_0$ is obtained by taking the subsidiary limit ![]() $k_\bot \rho _e \rightarrow 0$ in (J4), and substituting
$k_\bot \rho _e \rightarrow 0$ in (J4), and substituting ![]() $\tilde {\rho }_e = - \rho _e$:
$\tilde {\rho }_e = - \rho _e$:
 \begin{align} &\left[\tilde{\omega}_{e\|} \beta_e \sqrt{\rm \pi} \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} + \eta_e^T \beta_e \frac{\sqrt{\rm \pi}}{2} \left(\frac{1}{k_\|^2 \rho_e^2}-\frac{1}{2}\right) \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} + \mathrm{i} k_\|^2 \rho_e^2 \right]^2 \nonumber\\ &\quad+\left\{\tilde{\omega}_{e\|} \beta_e \, {\rm Re}{\,Z\!\left(\frac{1}{k_{\|} \rho_e}\right)} + \eta_e^T \beta_e \left[\frac{1}{2 k_{\|} \rho_e} + \left(\frac{1}{2 k_\|^2 \rho_e^2} - \frac{1}{4}\right) {\rm Re}{\,Z\!\left(\frac{1}{k_\| \rho_e}\right)}\right]\right\}^2 = 0 . \end{align}
\begin{align} &\left[\tilde{\omega}_{e\|} \beta_e \sqrt{\rm \pi} \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} + \eta_e^T \beta_e \frac{\sqrt{\rm \pi}}{2} \left(\frac{1}{k_\|^2 \rho_e^2}-\frac{1}{2}\right) \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} + \mathrm{i} k_\|^2 \rho_e^2 \right]^2 \nonumber\\ &\quad+\left\{\tilde{\omega}_{e\|} \beta_e \, {\rm Re}{\,Z\!\left(\frac{1}{k_{\|} \rho_e}\right)} + \eta_e^T \beta_e \left[\frac{1}{2 k_{\|} \rho_e} + \left(\frac{1}{2 k_\|^2 \rho_e^2} - \frac{1}{4}\right) {\rm Re}{\,Z\!\left(\frac{1}{k_\| \rho_e}\right)}\right]\right\}^2 = 0 . \end{align}
This can be factorised to give two roots; separating the complex frequency into real and imaginary parts via ![]() $\omega = \varpi + \mathrm {i} \gamma$, and defining
$\omega = \varpi + \mathrm {i} \gamma$, and defining
we have
 $$\begin{align} \tilde{\varpi}_{e\|} \beta_e &= \eta_e^T \beta_e \left(\frac{1}{2 k_\|^2 \rho_e^2}-\frac{1}{4}\right) + \frac{\left({\eta_e^T \beta_e}/{2 k_\| \rho_e} - k_\|^2 \rho_e^2\right) {\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)} }{\left[{\rm Re}{\, Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 + {\rm \pi}\exp{\left(-{2}/{k_\|^2 \rho_e^2}\right)}}, \end{align}$$
$$\begin{align} \tilde{\varpi}_{e\|} \beta_e &= \eta_e^T \beta_e \left(\frac{1}{2 k_\|^2 \rho_e^2}-\frac{1}{4}\right) + \frac{\left({\eta_e^T \beta_e}/{2 k_\| \rho_e} - k_\|^2 \rho_e^2\right) {\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)} }{\left[{\rm Re}{\, Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 + {\rm \pi}\exp{\left(-{2}/{k_\|^2 \rho_e^2}\right)}}, \end{align}$$ $$\begin{align}\tilde{\gamma}_{e\|} \beta_e &= \frac{\sqrt{\rm \pi}\left({\eta_e^T \beta_e}/{2 k_\| \rho_e} - k_\|^2 \rho_e^2\right) }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 \exp{\left({1}/{k_\|^2 \rho_e^2}\right)}+ {\rm \pi}\exp{\left(-{1}/{k_\|^2 \rho_e^2}\right)}} , \end{align}$$
$$\begin{align}\tilde{\gamma}_{e\|} \beta_e &= \frac{\sqrt{\rm \pi}\left({\eta_e^T \beta_e}/{2 k_\| \rho_e} - k_\|^2 \rho_e^2\right) }{\left[{\rm Re}{\,Z\!\left({1}/{k_\| \rho_e}\right)}\right]^2 \exp{\left({1}/{k_\|^2 \rho_e^2}\right)}+ {\rm \pi}\exp{\left(-{1}/{k_\|^2 \rho_e^2}\right)}} , \end{align}$$whence (3.5) follows immediately.
J.4. Approximate dispersion relation of CE ion-temperature-gradient-driven microinstabilities
We now explain the method used to characterise microinstabilities driven by the ion-temperature-gradient term. For these, we set the electron-temperature-gradient terms to zero, ![]() $\eta _e^T = 0$, assume the ordering
$\eta _e^T = 0$, assume the ordering ![]() $\tilde {\omega }_{i\|} \sim \eta _i$, and anticipate that such microinstabilities will occur on ion rather than electron scales, i.e.
$\tilde {\omega }_{i\|} \sim \eta _i$, and anticipate that such microinstabilities will occur on ion rather than electron scales, i.e. ![]() $k \rho _i \sim 1$. Under the ordering
$k \rho _i \sim 1$. Under the ordering ![]() $\tilde {\omega }_{i\|} \sim \eta _i \ll 1$, it follows that
$\tilde {\omega }_{i\|} \sim \eta _i \ll 1$, it follows that ![]() $\tilde {\omega }_{e\|} \sim \mu _e^{1/2} \tilde {\omega }_{i\|} \ll 1$; therefore, we can use (2.121) to quantity the contribution of Maxwellian electrons to the total dielectric tensor. However, since
$\tilde {\omega }_{e\|} \sim \mu _e^{1/2} \tilde {\omega }_{i\|} \ll 1$; therefore, we can use (2.121) to quantity the contribution of Maxwellian electrons to the total dielectric tensor. However, since ![]() $k \rho _i \sim 1$, we must consider the matrix
$k \rho _i \sim 1$, we must consider the matrix ![]() $\boldsymbol{\mathsf{M}}_{e}^{(0)}$ in the limit
$\boldsymbol{\mathsf{M}}_{e}^{(0)}$ in the limit ![]() $k_{\|} \rho _e \sim k_{\bot } \rho _e \sim \mu _e^{1/2} \ll 1$. Asymptotic forms of (2.121) appropriate for this limit are given by (G37), and lead toFootnote 11
$k_{\|} \rho _e \sim k_{\bot } \rho _e \sim \mu _e^{1/2} \ll 1$. Asymptotic forms of (2.121) appropriate for this limit are given by (G37), and lead toFootnote 11
 $$\begin{align} (\boldsymbol{\mathsf{M}}_{e}^{(0)})_{11} &= {O}\left[\exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)}\right] , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_{e}^{(0)})_{11} &= {O}\left[\exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)}\right] , \end{align}$$ We now combine (J16) with (2.121) for ![]() $\boldsymbol{\mathsf{M}}_i^{(0)}$ and (J3) for
$\boldsymbol{\mathsf{M}}_i^{(0)}$ and (J3) for ![]() $\boldsymbol{\mathsf{P}}_i^{(0)}$, and find the dispersion relation for CE ion-temperature-gradient-driven microinstabilities by substituting the dielectric tensor (2.108) into (2.117):
$\boldsymbol{\mathsf{P}}_i^{(0)}$, and find the dispersion relation for CE ion-temperature-gradient-driven microinstabilities by substituting the dielectric tensor (2.108) into (2.117):
 \begin{align} &\left[\tilde{\omega}_{i\|} F\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) + \eta_i {I}\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right)+ \mathrm{i} k_{\|}^2 d_i^2\right] \nonumber\\ &\quad\times \left[\tilde{\omega}_{i\|} H\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) + \eta_i {K}\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) +\mathrm{i} k^2 d_i^2\right] \nonumber\\ &\quad + \left[\tilde{\omega}_{i\|} \left[G\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) + k_{\|} \rho_i\right]+ \eta_i {J}\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right)\right]^2 = 0 , \end{align}
\begin{align} &\left[\tilde{\omega}_{i\|} F\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) + \eta_i {I}\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right)+ \mathrm{i} k_{\|}^2 d_i^2\right] \nonumber\\ &\quad\times \left[\tilde{\omega}_{i\|} H\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) + \eta_i {K}\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) +\mathrm{i} k^2 d_i^2\right] \nonumber\\ &\quad + \left[\tilde{\omega}_{i\|} \left[G\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right) + k_{\|} \rho_i\right]+ \eta_i {J}\!\left(k_{\|} \rho_i,k_{\bot} \rho_i\right)\right]^2 = 0 , \end{align}
where ![]() $d_i = c/\omega _{pi}$ is the ion inertial scale, and we have ordered
$d_i = c/\omega _{pi}$ is the ion inertial scale, and we have ordered ![]() $\eta _i \sim 1/\beta _i \sim k^2 d_i^2$. This dispersion relation is very similar to (J4), save for the addition of one term (the middle term in the third line of (J17)) providing a linear coupling between the
$\eta _i \sim 1/\beta _i \sim k^2 d_i^2$. This dispersion relation is very similar to (J4), save for the addition of one term (the middle term in the third line of (J17)) providing a linear coupling between the ![]() $\widehat {\delta \boldsymbol {E}}_1$ and
$\widehat {\delta \boldsymbol {E}}_1$ and ![]() $\widehat {\delta \boldsymbol {E}}_2$ components of the electric-field perturbation. Similarly to (J10), the dispersion relation (J17) can be written as a quadratic in
$\widehat {\delta \boldsymbol {E}}_2$ components of the electric-field perturbation. Similarly to (J10), the dispersion relation (J17) can be written as a quadratic in ![]() $\tilde {\omega }_{i\|} \beta _i$, which is then solved to give the following expression for the complex frequency:
$\tilde {\omega }_{i\|} \beta _i$, which is then solved to give the following expression for the complex frequency:
 \begin{equation} \omega = \frac{\varOmega_i}{\beta_i} k_{\|} \rho_i \frac{-\tilde{B}_{T} \pm \sqrt{\tilde{B}_{T}^2 + 4\tilde{A}_{\mathrm{T}}\tilde{C}_{T}}}{2 \tilde{A}_{T}} , \end{equation}
\begin{equation} \omega = \frac{\varOmega_i}{\beta_i} k_{\|} \rho_i \frac{-\tilde{B}_{T} \pm \sqrt{\tilde{B}_{T}^2 + 4\tilde{A}_{\mathrm{T}}\tilde{C}_{T}}}{2 \tilde{A}_{T}} , \end{equation}where
This expression is the one that is used to evaluate the real frequencies and growth rates of ion-scale CET microinstabilities in § 3.3.3.
J.4.1. Derivation of frequency and growth rate of the parallel CET slow-hydromagnetic-wave instability
We obtain the dispersion relation of the parallel slow-wave instability by considering the general dispersion relation (J17) of CE ion-temperature-gradient-driven instabilities in the limit ![]() $k_{\perp } \rightarrow 0$:
$k_{\perp } \rightarrow 0$:
 \begin{align} &\left[\tilde{\omega}_{i\|} \beta_i \sqrt{\rm \pi} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} + \eta_i \beta_i \frac{\sqrt{\rm \pi}}{2} \left(\frac{1}{k_\|^2 \rho_i^2}-\frac{1}{2}\right) \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} + \mathrm{i} k_\|^2 \rho_i^2 \right]^2 \nonumber\\ &\quad+ \left\{\tilde{\omega}_{i\|} \beta_i \, \left[{\rm Re}{\,Z\!\left(\frac{1}{k_\| \rho_i}\right)} + k_{\|} \rho_i\right] + \eta_i \beta_i \left[\frac{1}{2 k_{\|} \rho_i} + \left(\frac{1}{2 k_\|^2 \rho_i^2} - \frac{1}{4}\right) {\rm Re}{\,Z\!\left(\frac{1}{k_{\|} \rho_i}\right)}\right]\right\}^2 = 0 . \end{align}
\begin{align} &\left[\tilde{\omega}_{i\|} \beta_i \sqrt{\rm \pi} \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} + \eta_i \beta_i \frac{\sqrt{\rm \pi}}{2} \left(\frac{1}{k_\|^2 \rho_i^2}-\frac{1}{2}\right) \exp{\left(-\frac{1}{k_\|^2 \rho_i^2}\right)} + \mathrm{i} k_\|^2 \rho_i^2 \right]^2 \nonumber\\ &\quad+ \left\{\tilde{\omega}_{i\|} \beta_i \, \left[{\rm Re}{\,Z\!\left(\frac{1}{k_\| \rho_i}\right)} + k_{\|} \rho_i\right] + \eta_i \beta_i \left[\frac{1}{2 k_{\|} \rho_i} + \left(\frac{1}{2 k_\|^2 \rho_i^2} - \frac{1}{4}\right) {\rm Re}{\,Z\!\left(\frac{1}{k_{\|} \rho_i}\right)}\right]\right\}^2 = 0 . \end{align}
As before, this can be factorised to give two roots; for ![]() $\tilde {\omega }_{i\|} = \tilde {\varpi }_{i\|} + \mathrm {i} \tilde {\gamma }_{i\|}$ (cf. (J14a,b)), it follows that
$\tilde {\omega }_{i\|} = \tilde {\varpi }_{i\|} + \mathrm {i} \tilde {\gamma }_{i\|}$ (cf. (J14a,b)), it follows that
 $$\begin{gather} \tilde{\varpi}_{i\|} \beta_i = \eta_i \beta_i \left(\frac{1}{2 k_\|^2 \rho_i^2}-\frac{1}{4}\right) + \frac{k_{\|} \rho_i \left[{\rm Re}{\,Z\!\left(\dfrac{1}{k_\| \rho_i}\right)} + k_{\|} \rho_i\right] \left({\eta_i \beta_i}/{4} - k_\| \rho_i\right) }{\left[ {\rm Re}{\,Z\!\left(\dfrac{1}{k_\| \rho_i}\right)} + k_{\|} \rho_i\right]^2 + {\rm \pi}\exp{\left(-\dfrac{2}{k_\|^2 \rho_i^2}\right)}} , \end{gather}$$
$$\begin{gather} \tilde{\varpi}_{i\|} \beta_i = \eta_i \beta_i \left(\frac{1}{2 k_\|^2 \rho_i^2}-\frac{1}{4}\right) + \frac{k_{\|} \rho_i \left[{\rm Re}{\,Z\!\left(\dfrac{1}{k_\| \rho_i}\right)} + k_{\|} \rho_i\right] \left({\eta_i \beta_i}/{4} - k_\| \rho_i\right) }{\left[ {\rm Re}{\,Z\!\left(\dfrac{1}{k_\| \rho_i}\right)} + k_{\|} \rho_i\right]^2 + {\rm \pi}\exp{\left(-\dfrac{2}{k_\|^2 \rho_i^2}\right)}} , \end{gather}$$ $$\begin{gather}\tilde{\gamma}_{i\|} \beta_i = \frac{\sqrt{\rm \pi} k_{\|} \rho_i \left({\eta_i \beta_i}/{4} - k_\| \rho_i\right) }{\left[{\rm Re}{\,Z\!\left(\dfrac{1}{k_\| \rho_i}\right)} + k_{\|} \rho_i\right]^2 \exp{\left(\dfrac{1}{k_\|^2 \rho_i^2}\right)}+ {\rm \pi}\exp{\left(-\dfrac{1}{k_\|^2 \rho_i^2}\right)}} . \end{gather}$$
$$\begin{gather}\tilde{\gamma}_{i\|} \beta_i = \frac{\sqrt{\rm \pi} k_{\|} \rho_i \left({\eta_i \beta_i}/{4} - k_\| \rho_i\right) }{\left[{\rm Re}{\,Z\!\left(\dfrac{1}{k_\| \rho_i}\right)} + k_{\|} \rho_i\right]^2 \exp{\left(\dfrac{1}{k_\|^2 \rho_i^2}\right)}+ {\rm \pi}\exp{\left(-\dfrac{1}{k_\|^2 \rho_i^2}\right)}} . \end{gather}$$These can be rearranged to give (3.13).
J.4.2. Derivation of frequency and growth rate of the CET long-wavelength KAW instability
In the limit ![]() $k_{\|} \rho _i \ll 1$,
$k_{\|} \rho _i \ll 1$, ![]() $k_\perp \rho _i \sim 1$, the general dispersion relation (J17) of CE ion-temperature-gradient-driven instabilities becomes
$k_\perp \rho _i \sim 1$, the general dispersion relation (J17) of CE ion-temperature-gradient-driven instabilities becomes
 \begin{align} &\left[\tilde{\omega}_{i\|} (1 - \mathcal{F}_i ) - \frac{\eta_i}{2} \mathcal{G}_i \right]^2 \nonumber\\ &\quad + \frac{k_{{\perp}}^2 \rho_i^2}{\beta_i} \left[ \mathrm{i} \sqrt{\rm \pi} \left(\mathcal{F}_i + \sqrt{\frac{\mu_e Z^2}{\tau}}\right) \tilde{\omega}_{i\|} - \frac{1}{\beta_i} + \frac{\mathrm{i} \sqrt{\rm \pi} \eta_i}{2} \left( \mathcal{G}_i -\frac{1}{2} \mathcal{F}_i \right) \right] = 0 , \end{align}
\begin{align} &\left[\tilde{\omega}_{i\|} (1 - \mathcal{F}_i ) - \frac{\eta_i}{2} \mathcal{G}_i \right]^2 \nonumber\\ &\quad + \frac{k_{{\perp}}^2 \rho_i^2}{\beta_i} \left[ \mathrm{i} \sqrt{\rm \pi} \left(\mathcal{F}_i + \sqrt{\frac{\mu_e Z^2}{\tau}}\right) \tilde{\omega}_{i\|} - \frac{1}{\beta_i} + \frac{\mathrm{i} \sqrt{\rm \pi} \eta_i}{2} \left( \mathcal{G}_i -\frac{1}{2} \mathcal{F}_i \right) \right] = 0 , \end{align}
where we remind the reader that ![]() $\mathcal {F}_i = \mathcal {F}(k_{\perp } \rho _i)$,
$\mathcal {F}_i = \mathcal {F}(k_{\perp } \rho _i)$, ![]() $\mathcal {G}_i = \mathcal {G}(k_{\perp } \rho _i)$, with the functions
$\mathcal {G}_i = \mathcal {G}(k_{\perp } \rho _i)$, with the functions ![]() $\mathcal {F}(\alpha )$ and
$\mathcal {F}(\alpha )$ and ![]() $\mathcal {G}(\alpha )$ being defined by (3.24). Equation (3.22) for the complex frequency of the CET KAW modes in the main text is then derived by solving (J24) for
$\mathcal {G}(\alpha )$ being defined by (3.24). Equation (3.22) for the complex frequency of the CET KAW modes in the main text is then derived by solving (J24) for ![]() $\tilde {\omega }_{i\|} = {\omega }/{k_{\|} v_{\mathrm {th}i}}$.
$\tilde {\omega }_{i\|} = {\omega }/{k_{\|} v_{\mathrm {th}i}}$.
Appendix K. Methodology for characterising CES microinstabilities
This appendix outlines the method used to determine the growth rates of microinstabilities driven by the CE electron- and ion-shear terms. Once again (cf. Appendix J), § 2.5 presents the general framework of our approach: determine a simplified algebraic dispersion relation satisfied by the (complex) frequencies ![]() $\omega$ of CES microinstabilities with parallel and perpendicular wavenumber
$\omega$ of CES microinstabilities with parallel and perpendicular wavenumber ![]() $k_{\|}$ and
$k_{\|}$ and ![]() $k_{\perp }$ under the assumption that they are low frequency (viz.
$k_{\perp }$ under the assumption that they are low frequency (viz. ![]() $\omega \ll k_{\|} v_{\mathrm {th}s}$; cf. (2.94)), solve for
$\omega \ll k_{\|} v_{\mathrm {th}s}$; cf. (2.94)), solve for ![]() $\omega$, then calculate the growth rate
$\omega$, then calculate the growth rate ![]() $\gamma$ from its imaginary part (and the real frequency
$\gamma$ from its imaginary part (and the real frequency ![]() $\varpi$ from its real part). To construct the dispersion relation, we first need to know the tensor
$\varpi$ from its real part). To construct the dispersion relation, we first need to know the tensor ![]() $\boldsymbol{\mathsf{P}}_{s}^{(0)}$ for a CE distribution function of the form (4.1); this result is given in Appendix K.1. Then, in Appendix K.2.1, we determine an approximate quadratic dispersion relation for CES microinstabilities, show in Appendix K.2.2 how that dispersion relation can be used in certain cases to evaluate the CES instability thresholds semi-analytically, then demonstrate the significant shortcomings of the quadratic approximation in Appendix K.2.3. In Appendix K.3.1, we address these shortcomings by constructing a revised quartic dispersion relation for CES microinstabilities. This quartic dispersion relation is then used to derive simplified dispersion relations for the various different CES microinstabilities discussed in the main text: the mirror instability in Appendix K.3.2, the parallel (CES) whistler instability in Appendix K.3.3, the transverse instability in Appendix K.3.4, the electron mirror instability in Appendix K.3.5, the parallel, oblique and critical-line firehose instabilities in Appendices K.3.6, K.3.7 and K.3.8, the parallel and oblique electron firehose instabilities in Appendices K.3.9 and K.3.10, the EST instability in Appendix K.3.11 and the whisper instability in Appendix K.3.12. Finally, in Appendix K.3.13, we derive the dispersion relation of the CET ordinary-mode instability – the one CES (or CET) microinstability that does not satisfy
$\boldsymbol{\mathsf{P}}_{s}^{(0)}$ for a CE distribution function of the form (4.1); this result is given in Appendix K.1. Then, in Appendix K.2.1, we determine an approximate quadratic dispersion relation for CES microinstabilities, show in Appendix K.2.2 how that dispersion relation can be used in certain cases to evaluate the CES instability thresholds semi-analytically, then demonstrate the significant shortcomings of the quadratic approximation in Appendix K.2.3. In Appendix K.3.1, we address these shortcomings by constructing a revised quartic dispersion relation for CES microinstabilities. This quartic dispersion relation is then used to derive simplified dispersion relations for the various different CES microinstabilities discussed in the main text: the mirror instability in Appendix K.3.2, the parallel (CES) whistler instability in Appendix K.3.3, the transverse instability in Appendix K.3.4, the electron mirror instability in Appendix K.3.5, the parallel, oblique and critical-line firehose instabilities in Appendices K.3.6, K.3.7 and K.3.8, the parallel and oblique electron firehose instabilities in Appendices K.3.9 and K.3.10, the EST instability in Appendix K.3.11 and the whisper instability in Appendix K.3.12. Finally, in Appendix K.3.13, we derive the dispersion relation of the CET ordinary-mode instability – the one CES (or CET) microinstability that does not satisfy ![]() $\omega \ll k_{\|} v_{\mathrm {th}s}$ for either electrons or ions (see § 2.5.8) – directly from the hot-plasma dispersion relation.
$\omega \ll k_{\|} v_{\mathrm {th}s}$ for either electrons or ions (see § 2.5.8) – directly from the hot-plasma dispersion relation.
K.1. Dielectric response of CE shear terms
First, we evaluate the elements of ![]() $\boldsymbol{\mathsf{P}}_{s}^{(0)}$:
$\boldsymbol{\mathsf{P}}_{s}^{(0)}$:
 $$\begin{align} (\boldsymbol{\mathsf{P}}_{s}^{(0)})_{11} &= \epsilon_s \frac{k^2}{k_{\|}^2} W\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{P}}_{s}^{(0)})_{11} &= \epsilon_s \frac{k^2}{k_{\|}^2} W\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s\right) , \end{align}$$
where the special functions ![]() $W(x,y)$,
$W(x,y)$, ![]() ${Y}(x,y)$ and
${Y}(x,y)$ and ![]() $X(x,y)$ are defined by (G97). These results are derived in Appendix G.4.
$X(x,y)$ are defined by (G97). These results are derived in Appendix G.4.
K.2. Quadratic approximation to dispersion relation of CE shear-driven microinstabilities
K.2.1. Derivation
Considering the relative magnitude of ![]() $\tilde {\omega }_{i\|} = \omega /k_{\|} v_{\mathrm {th}i}$ and
$\tilde {\omega }_{i\|} = \omega /k_{\|} v_{\mathrm {th}i}$ and ![]() $\tilde {\omega }_{e\|} = \omega /k_{\|} v_{\mathrm {th}e} \ll \tilde {\omega }_{i\|}$, we observe that, unlike CET microinstabilities, CES microinstabilities satisfy the low-frequency condition (2.94) for both electrons and ions. This claim holds because any microinstability involving the CE electron-shear term must satisfy
$\tilde {\omega }_{e\|} = \omega /k_{\|} v_{\mathrm {th}e} \ll \tilde {\omega }_{i\|}$, we observe that, unlike CET microinstabilities, CES microinstabilities satisfy the low-frequency condition (2.94) for both electrons and ions. This claim holds because any microinstability involving the CE electron-shear term must satisfy ![]() $\tilde {\omega }_{e\|} \sim \epsilon _e \ll (m_e/m_i)^{1/2}$, where the last inequality arises from the scaling relation
$\tilde {\omega }_{e\|} \sim \epsilon _e \ll (m_e/m_i)^{1/2}$, where the last inequality arises from the scaling relation ![]() $\epsilon _e \sim (m_e/m_i)^{1/2} \epsilon _i$ given by (2.42d); thus, from the scaling relation (2.106) with
$\epsilon _e \sim (m_e/m_i)^{1/2} \epsilon _i$ given by (2.42d); thus, from the scaling relation (2.106) with ![]() $T_e = T_i$, it follows that
$T_e = T_i$, it follows that ![]() $\tilde {\omega }_{i\|} \sim \epsilon _e (m_i/m_e)^{1/2} \sim \epsilon _i \ll 1$. Therefore, it is consistent to expand both the Maxwellian electron and ion terms in
$\tilde {\omega }_{i\|} \sim \epsilon _e (m_i/m_e)^{1/2} \sim \epsilon _i \ll 1$. Therefore, it is consistent to expand both the Maxwellian electron and ion terms in ![]() $\tilde {\omega }_{s\|} \ll 1$.
$\tilde {\omega }_{s\|} \ll 1$.
We therefore initially approximate ![]() $\boldsymbol {\mathfrak {E}}$ as follows:
$\boldsymbol {\mathfrak {E}}$ as follows:
 \begin{equation} \boldsymbol{\mathfrak{E}} \approx \tilde{\omega}_{e\|} \boldsymbol{\mathfrak{E}}^{(0)} = \frac{\omega_{{\rm p}e}^2}{\omega^2} \left(\sum_s \tilde{\omega}_{s\|} \mu_s \boldsymbol{\mathsf{M}}_s^{(0)} + \sum_s \mu_s \boldsymbol{\mathsf{P}}_s^{(0)} \right) , \end{equation}
\begin{equation} \boldsymbol{\mathfrak{E}} \approx \tilde{\omega}_{e\|} \boldsymbol{\mathfrak{E}}^{(0)} = \frac{\omega_{{\rm p}e}^2}{\omega^2} \left(\sum_s \tilde{\omega}_{s\|} \mu_s \boldsymbol{\mathsf{M}}_s^{(0)} + \sum_s \mu_s \boldsymbol{\mathsf{P}}_s^{(0)} \right) , \end{equation}
where the expansion of ![]() $\boldsymbol{\mathsf{M}}_s$ and
$\boldsymbol{\mathsf{M}}_s$ and ![]() $\boldsymbol{\mathsf{P}}_s$ in
$\boldsymbol{\mathsf{P}}_s$ in ![]() $\tilde {\omega }_{s\|}$, i.e.
$\tilde {\omega }_{s\|}$, i.e.
applies to both ion and electron species. By analogy to the derivation presented in § 2.5.5, this approximation gives rise to a simplified dispersion relation (cf. (2.117))
We emphasise that, here, each component of ![]() $\boldsymbol {\mathfrak {E}}^{(0)}$ has both electron and ion contributions. Expressing
$\boldsymbol {\mathfrak {E}}^{(0)}$ has both electron and ion contributions. Expressing ![]() $\tilde {\omega }_{i\|} = \tilde {\omega }_{e\|} \mu _e^{-1/2}$ in (K2), (K4) can be written as
$\tilde {\omega }_{i\|} = \tilde {\omega }_{e\|} \mu _e^{-1/2}$ in (K2), (K4) can be written as
 \begin{align} & \left[\tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{11} + (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{11} - k^2 d_e^2\right] \nonumber\\ & \quad \times \left[\tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{22} + (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{22} - k^2 d_e^2\right] \nonumber\\ & \quad + \left[ \tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{12} + (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{12} \right]^2 = 0 . \end{align}
\begin{align} & \left[\tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{11} + (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{11} - k^2 d_e^2\right] \nonumber\\ & \quad \times \left[\tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{22} + (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{22} - k^2 d_e^2\right] \nonumber\\ & \quad + \left[ \tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{12} + (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{12} \right]^2 = 0 . \end{align}
Combining the expressions (K1) for ![]() $\boldsymbol{\mathsf{P}}_s^{(0)}$ with (2.121) for
$\boldsymbol{\mathsf{P}}_s^{(0)}$ with (2.121) for ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ and substituting
$\boldsymbol{\mathsf{M}}_s^{(0)}$ and substituting ![]() $\boldsymbol{\mathsf{M}}_s^{(0)}$ and
$\boldsymbol{\mathsf{M}}_s^{(0)}$ and ![]() $\boldsymbol{\mathsf{P}}_s^{(0)}$ into (K5) gives
$\boldsymbol{\mathsf{P}}_s^{(0)}$ into (K5) gives
 \begin{align} & \left[\mathrm{i} \tilde{\omega}_{e\|} \left( F_e + \mu_e^{1/2} F_i \right) +\epsilon_e \left( W_e + \mu_e^{1/2} W_i \right)- k_{\|}^2 d_e^2\right] \nonumber\\ & \quad \times \left[ \mathrm{i} \tilde{\omega}_{e\|} \left( H_e + \mu_e^{1/2} H_i \right) + \epsilon_e \left( {Y}_e + \mu_e^{1/2} {Y}_i \right)- k^2 d_e^2\right] \nonumber\\ & \quad +\left[\mathrm{i} \tilde{\omega}_{e\|} \left( G_e + \mu_e^{1/2} G_i \right) + \epsilon_e \left( X_e + \mu_e^{1/2} X_i \right) \right]^2 = 0 , \end{align}
\begin{align} & \left[\mathrm{i} \tilde{\omega}_{e\|} \left( F_e + \mu_e^{1/2} F_i \right) +\epsilon_e \left( W_e + \mu_e^{1/2} W_i \right)- k_{\|}^2 d_e^2\right] \nonumber\\ & \quad \times \left[ \mathrm{i} \tilde{\omega}_{e\|} \left( H_e + \mu_e^{1/2} H_i \right) + \epsilon_e \left( {Y}_e + \mu_e^{1/2} {Y}_i \right)- k^2 d_e^2\right] \nonumber\\ & \quad +\left[\mathrm{i} \tilde{\omega}_{e\|} \left( G_e + \mu_e^{1/2} G_i \right) + \epsilon_e \left( X_e + \mu_e^{1/2} X_i \right) \right]^2 = 0 , \end{align}
where we have used ![]() $\epsilon _i = \epsilon _e \mu _e^{-1/2}$. For brevity of notation, we have also defined
$\epsilon _i = \epsilon _e \mu _e^{-1/2}$. For brevity of notation, we have also defined ![]() $F_s \equiv F(k_{\|} \tilde {\rho }_s,k_{\bot } \tilde {\rho }_s)$,
$F_s \equiv F(k_{\|} \tilde {\rho }_s,k_{\bot } \tilde {\rho }_s)$, ![]() $G_s \equiv G(k_{\|} \tilde {\rho }_s,k_{\bot } \tilde {\rho }_s)$ and so on.
$G_s \equiv G(k_{\|} \tilde {\rho }_s,k_{\bot } \tilde {\rho }_s)$ and so on.
Using (2.58b) for the terms ![]() $\propto d_e^2$ explicitly introduces a
$\propto d_e^2$ explicitly introduces a ![]() $\beta _e$ dependence into (K6). After some elementary manipulations, we obtain the quadratic
$\beta _e$ dependence into (K6). After some elementary manipulations, we obtain the quadratic
where
 \begin{align} B_{\mathrm{S}} & = \left(H_e+\mu_e^{1/2} H_i\right)\left[k_{\|}^2 \rho_e^2 - \epsilon_e \beta_e \left(W_e+\mu_e^{1/2} W_i\right)\right] - 2 \epsilon_e \beta_e \left(G_e+\mu_e^{1/2} G_i\right) \left(X_e+\mu_e^{1/2} X_i\right) \nonumber\\ &\quad +\left(F_e+\mu_e^{1/2} F_i\right)\left[k^2 \rho_e^2 - \epsilon_e \beta_e \left({Y}_e+\mu_e^{1/2} {Y}_i\right)\right] , \end{align}
\begin{align} B_{\mathrm{S}} & = \left(H_e+\mu_e^{1/2} H_i\right)\left[k_{\|}^2 \rho_e^2 - \epsilon_e \beta_e \left(W_e+\mu_e^{1/2} W_i\right)\right] - 2 \epsilon_e \beta_e \left(G_e+\mu_e^{1/2} G_i\right) \left(X_e+\mu_e^{1/2} X_i\right) \nonumber\\ &\quad +\left(F_e+\mu_e^{1/2} F_i\right)\left[k^2 \rho_e^2 - \epsilon_e \beta_e \left({Y}_e+\mu_e^{1/2} {Y}_i\right)\right] , \end{align} \begin{align} C_{S} & = \left[k_{\|}^2 \rho_e^2 - \epsilon_e \beta_e \left(W_e+\mu_e^{1/2} W_i\right)\right] \left[k^2 \rho_e^2 - \epsilon_e \beta_e \left({Y}_e+\mu_e^{1/2} {\rm Y}_i\right)\right] \nonumber\\ &\quad + \epsilon_e^2 \beta_e^2 \left(X_e+\mu_e^{1/2} X_i\right)^2 . \end{align}
\begin{align} C_{S} & = \left[k_{\|}^2 \rho_e^2 - \epsilon_e \beta_e \left(W_e+\mu_e^{1/2} W_i\right)\right] \left[k^2 \rho_e^2 - \epsilon_e \beta_e \left({Y}_e+\mu_e^{1/2} {\rm Y}_i\right)\right] \nonumber\\ &\quad + \epsilon_e^2 \beta_e^2 \left(X_e+\mu_e^{1/2} X_i\right)^2 . \end{align}As before, this can be solved explicitly for the complex frequency
From this expression, we can extract the real frequency ![]() $\varpi$ and the growth rate
$\varpi$ and the growth rate ![]() $\gamma$ explicitly. In the case when
$\gamma$ explicitly. In the case when ![]() $4A_{S}C_{S} > B_{S}^2$, we have two oppositely propagating modes with the same growth rate:
$4A_{S}C_{S} > B_{S}^2$, we have two oppositely propagating modes with the same growth rate:
For ![]() $4A_{S}C_{S} < B_{S}^2$, both modes are non-propagating, with distinct growth rates
$4A_{S}C_{S} < B_{S}^2$, both modes are non-propagating, with distinct growth rates
K.2.2. Semi-analytic estimates of CES instability thresholds using quadratic approximation
In the case of non-propagating modes whose growth rate is given by (K11), we can determine semi-analytic formulae for the thresholds of any instabilities. This is done by noting that, at marginal stability, ![]() $\tilde {\omega }_{e\|} = 0$. Therefore, it follows from (K7) that
$\tilde {\omega }_{e\|} = 0$. Therefore, it follows from (K7) that ![]() $C_{S} = 0$, or, equivalently,
$C_{S} = 0$, or, equivalently,
This is a quadratic in ![]() $\epsilon _e \beta _e$ which can be solved exactly to give the threshold value of
$\epsilon _e \beta _e$ which can be solved exactly to give the threshold value of ![]() $\epsilon _e \beta _e$ as a function of perpendicular and parallel wavenumber,
$\epsilon _e \beta _e$ as a function of perpendicular and parallel wavenumber,
 \begin{align} \epsilon_e \beta_e & = \tfrac{1}{2}\left[\left(W_e+\mu_e^{1/2} W_i\right) \left({Y}_e+\mu_e^{1/2} {Y}_i\right) + \left(X_e+\mu_e^{1/2} X_i\right)^2\right]^{{-}1} \nonumber\\ &\quad \times \left(\vphantom{\left[\left(W_e+\mu_e^{1/2} W_i\right) \left({Y}_e+\mu_e^{1/2} {Y}_i\right) + \left(X_e+\mu_e^{1/2} X_i\right)^2\right]}k^2 \rho_e^2 \left(W_e+\mu_e^{1/2} W_i\right) + k_{\|}^2 \rho_e^2 \left({Y}_e+\mu_e^{1/2} {Y}_i\right)\right. \nonumber\\ & \quad\pm\left\{\left[k^2 \rho_e^2 \left(W_e+\mu_e^{1/2} W_i\right) + k_{\|}^2 \rho_e^2 \left({Y}_e+\mu_e^{1/2} {Y}_i\right)\right]^2 \right. \nonumber\\ &\quad \left.\left. - 4 k_{\|}^2 k^2 \rho_e^4 \left[\left(W_e+\mu_e^{1/2} W_i\right) \left({Y}_e+\mu_e^{1/2} {Y}_i\right) + \left(X_e+\mu_e^{1/2} X_i\right)^2\right]\right\}^{1/2} \right) . \end{align}
\begin{align} \epsilon_e \beta_e & = \tfrac{1}{2}\left[\left(W_e+\mu_e^{1/2} W_i\right) \left({Y}_e+\mu_e^{1/2} {Y}_i\right) + \left(X_e+\mu_e^{1/2} X_i\right)^2\right]^{{-}1} \nonumber\\ &\quad \times \left(\vphantom{\left[\left(W_e+\mu_e^{1/2} W_i\right) \left({Y}_e+\mu_e^{1/2} {Y}_i\right) + \left(X_e+\mu_e^{1/2} X_i\right)^2\right]}k^2 \rho_e^2 \left(W_e+\mu_e^{1/2} W_i\right) + k_{\|}^2 \rho_e^2 \left({Y}_e+\mu_e^{1/2} {Y}_i\right)\right. \nonumber\\ & \quad\pm\left\{\left[k^2 \rho_e^2 \left(W_e+\mu_e^{1/2} W_i\right) + k_{\|}^2 \rho_e^2 \left({Y}_e+\mu_e^{1/2} {Y}_i\right)\right]^2 \right. \nonumber\\ &\quad \left.\left. - 4 k_{\|}^2 k^2 \rho_e^4 \left[\left(W_e+\mu_e^{1/2} W_i\right) \left({Y}_e+\mu_e^{1/2} {Y}_i\right) + \left(X_e+\mu_e^{1/2} X_i\right)^2\right]\right\}^{1/2} \right) . \end{align}Expression (K13) is used in §§ 4.4.1 and 4.4.7 to evaluate the wavevector-dependent thresholds of the CES ion and electron firehose instabilities, respectively.
K.2.3. Shortcomings of quadratic approximation
In contrast to quadratic approximations to the dispersion relations of CET microinstabilities being sufficient to characterise all instabilities of note (see, e.g. Appendix J.3), not all CES microinstabilities are captured by the quadratic dispersion relation (K7), because there are important microinstabilities whose correct description requires keeping higher-order terms in the ![]() $\tilde {\omega }_{s\|} \ll 1$ expansion. The mathematical reason for this is that some microinstabilities occur in wavenumber regimes where either
$\tilde {\omega }_{s\|} \ll 1$ expansion. The mathematical reason for this is that some microinstabilities occur in wavenumber regimes where either ![]() $k_{\|} \rho _i \ll 1$ and/or
$k_{\|} \rho _i \ll 1$ and/or ![]() $k_{\|} \rho _e \ll 1$. As a result, the issues raised in § 2.5.6 regarding the commutability of the
$k_{\|} \rho _e \ll 1$. As a result, the issues raised in § 2.5.6 regarding the commutability of the ![]() $\tilde {\omega }_{s\|} \ll 1$ and
$\tilde {\omega }_{s\|} \ll 1$ and ![]() $k_{\|} \rho _s \ll 1$ limits must be carefully resolved. In Appendix G.1.6, it is shown that, if
$k_{\|} \rho _s \ll 1$ limits must be carefully resolved. In Appendix G.1.6, it is shown that, if ![]() $k_{\|} \rho _s \ll 1/\log {(1/\tilde {\omega }_{s\|})}$, then the dominant contributions to
$k_{\|} \rho _s \ll 1/\log {(1/\tilde {\omega }_{s\|})}$, then the dominant contributions to ![]() $(\boldsymbol{\mathsf{M}}_s)_{xx}$,
$(\boldsymbol{\mathsf{M}}_s)_{xx}$, ![]() $(\boldsymbol{\mathsf{M}}_s)_{xz}$ and
$(\boldsymbol{\mathsf{M}}_s)_{xz}$ and ![]() $(\boldsymbol{\mathsf{M}}_s)_{zz}$ arise from the quadratic term in
$(\boldsymbol{\mathsf{M}}_s)_{zz}$ arise from the quadratic term in ![]() $\tilde {\omega }_{s\|} \ll 1$ expansion, namely
$\tilde {\omega }_{s\|} \ll 1$ expansion, namely
If ![]() $k_{\bot } \rho _s \ll k_{\|} \rho _s \tilde {\omega }_{s\|}^{1/2}$, then
$k_{\bot } \rho _s \ll k_{\|} \rho _s \tilde {\omega }_{s\|}^{1/2}$, then
In the ![]() $\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$ coordinate frame, this means that the dominant contributions to each component of
$\{\boldsymbol {e}_1,\boldsymbol {e}_2,\boldsymbol {e}_3\}$ coordinate frame, this means that the dominant contributions to each component of ![]() $\boldsymbol{\mathsf{M}}_{s}$ are (see Appendix G.1.3)
$\boldsymbol{\mathsf{M}}_{s}$ are (see Appendix G.1.3)
 $$\begin{align} (\boldsymbol{\mathsf{M}}_{s})_{11} &\approx \tilde{\omega}_{s\|}^2 (\boldsymbol{\mathsf{M}}_{s}^{(1)})_{11} = \frac{k^2} {k_{\|}^2} {\omega}_{s\|}^2 (\boldsymbol{\mathsf{M}}_{s}^{(1)})_{xx} + 2 \tilde{\omega}_{s\|}^2 \left[\frac{k_{\bot}^2}{k^2} + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] , \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_{s})_{11} &\approx \tilde{\omega}_{s\|}^2 (\boldsymbol{\mathsf{M}}_{s}^{(1)})_{11} = \frac{k^2} {k_{\|}^2} {\omega}_{s\|}^2 (\boldsymbol{\mathsf{M}}_{s}^{(1)})_{xx} + 2 \tilde{\omega}_{s\|}^2 \left[\frac{k_{\bot}^2}{k^2} + \frac{k_{\bot}}{k_{\|}} L\!\left(k_{\|} \tilde{\rho}_s,k_{\bot} \tilde{\rho}_s \right)\right] , \end{align}$$
where the special functions ![]() $L(x,y)$ and
$L(x,y)$ and ![]() $N(x,y)$ are given by (G32). The quadratic dispersion relation (K7) must, therefore, be revised to capture correctly all relevant microinstabilities.
$N(x,y)$ are given by (G32). The quadratic dispersion relation (K7) must, therefore, be revised to capture correctly all relevant microinstabilities.
K.3. Quartic approximation to dispersion relation of CE shear-driven microinstabilities
K.3.1. Derivation of general quartic CES dispersion relation
To assess how the new terms identified in § K.2.3 change the dispersion relation (K6), we now return to the full hot-plasma dispersion relation (2.75), which we write in the form
Reminding the reader that, for a two-species plasma,
 \begin{equation} \boldsymbol{\mathfrak{E}} = \sum_s \boldsymbol{\mathfrak{E}}_s = \frac{\omega_{{\rm p}e}^2}{\omega^2} \sum_s \mu_s \left(\boldsymbol{\mathsf{M}}_s + \boldsymbol{\mathsf{P}}_s \right) , \end{equation}
\begin{equation} \boldsymbol{\mathfrak{E}} = \sum_s \boldsymbol{\mathfrak{E}}_s = \frac{\omega_{{\rm p}e}^2}{\omega^2} \sum_s \mu_s \left(\boldsymbol{\mathsf{M}}_s + \boldsymbol{\mathsf{P}}_s \right) , \end{equation}
and also that the electrostatic component of the dielectric tensor is determined by the Maxwellian components only (which in turn are equal for electrons and ions when ![]() $T_i = T_e$ – see Appendix D.2), viz.
$T_i = T_e$ – see Appendix D.2), viz.
 \begin{equation} \mathfrak{E}_{33} \approx \tilde{\omega}_{e\|}^2 \mathfrak{E}_{33}^{(1)} = \frac{\omega_{{\rm p}e}^2}{\omega^2} \sum_s \mu_s \tilde{\omega}_{s\|}^2 (\boldsymbol{\mathsf{M}}_s^{(1)})_{33} = \frac{4 \omega_{{\rm p}e}^2}{\omega^2} \tilde{\omega}_{e\|}^2 \frac{k_{\|}^2}{k^2} , \end{equation}
\begin{equation} \mathfrak{E}_{33} \approx \tilde{\omega}_{e\|}^2 \mathfrak{E}_{33}^{(1)} = \frac{\omega_{{\rm p}e}^2}{\omega^2} \sum_s \mu_s \tilde{\omega}_{s\|}^2 (\boldsymbol{\mathsf{M}}_s^{(1)})_{33} = \frac{4 \omega_{{\rm p}e}^2}{\omega^2} \tilde{\omega}_{e\|}^2 \frac{k_{\|}^2}{k^2} , \end{equation}
we show in Appendix G.1.7 that, in the limit ![]() $k_{\|} \rho _s \ll 1$,
$k_{\|} \rho _s \ll 1$,
 $$\begin{align} \frac{\left[(\boldsymbol{\mathsf{M}}_{s})_{13}\right]^2}{(\boldsymbol{\mathsf{M}}_s^{(1)})_{33}} &\lesssim (\boldsymbol{\mathsf{M}}_{s})_{11} , \end{align}$$
$$\begin{align} \frac{\left[(\boldsymbol{\mathsf{M}}_{s})_{13}\right]^2}{(\boldsymbol{\mathsf{M}}_s^{(1)})_{33}} &\lesssim (\boldsymbol{\mathsf{M}}_{s})_{11} , \end{align}$$ $$\begin{align}\frac{\left[(\boldsymbol{\mathsf{M}}_{s})_{23}\right]^2}{(\boldsymbol{\mathsf{M}}_s^{(1)})_{33}} &\lesssim \tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{s})_{22} \ll (\boldsymbol{\mathsf{M}}_{s})_{22} . \end{align}$$
$$\begin{align}\frac{\left[(\boldsymbol{\mathsf{M}}_{s})_{23}\right]^2}{(\boldsymbol{\mathsf{M}}_s^{(1)})_{33}} &\lesssim \tilde{\omega}_{e\|} (\boldsymbol{\mathsf{M}}_{s})_{22} \ll (\boldsymbol{\mathsf{M}}_{s})_{22} . \end{align}$$
On the other hand, the shear-perturbation components ![]() $\boldsymbol{\mathsf{P}}_s$ satisfy
$\boldsymbol{\mathsf{P}}_s$ satisfy
Substituting for ![]() $\boldsymbol{\mathsf{M}}_{s}$ and
$\boldsymbol{\mathsf{M}}_{s}$ and ![]() $\boldsymbol{\mathsf{P}}_{s}$ in (K18) using (K16) and (K3b), respectively, and then substituting (K18) into (K17), we obtain the following quartic dispersion relation:
$\boldsymbol{\mathsf{P}}_{s}$ in (K18) using (K16) and (K3b), respectively, and then substituting (K18) into (K17), we obtain the following quartic dispersion relation:
 \begin{align} & \left\{\tilde{\omega}_{e\|}^2 \left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} - \frac{(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}^{2}}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} \right] + (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{11} - k^2 d_e^2\right\} \nonumber\\ & \quad \times \left\{\tilde{\omega}_{e\|}^2 \left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{22} \right] + \tilde{\omega}_{e\|} \left[(\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{22} \right]+ (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{22} - k^2 d_e^2\right\} \nonumber\\ & \quad + \tilde{\omega}_{e\|}^2 \left[(\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{12} \right]^2 = 0 . \end{align}
\begin{align} & \left\{\tilde{\omega}_{e\|}^2 \left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} - \frac{(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}^{2}}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} \right] + (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{11} - k^2 d_e^2\right\} \nonumber\\ & \quad \times \left\{\tilde{\omega}_{e\|}^2 \left[(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{22} \right] + \tilde{\omega}_{e\|} \left[(\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{22} \right]+ (\boldsymbol{\mathsf{P}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{P}}_{i}^{(0)})_{22} - k^2 d_e^2\right\} \nonumber\\ & \quad + \tilde{\omega}_{e\|}^2 \left[(\boldsymbol{\mathsf{M}}_{e}^{(0)} + \mu_e^{1/2} \boldsymbol{\mathsf{M}}_{i}^{(0)})_{12} \right]^2 = 0 . \end{align}
We have assumed ![]() $k \rho _e \ll k \rho _i \ll 1$ and so we now have additional quadratic terms for both electrons and ions, as explained in § K.2.3.
$k \rho _e \ll k \rho _i \ll 1$ and so we now have additional quadratic terms for both electrons and ions, as explained in § K.2.3.
We note that the dispersion relation (K22) is similar to (K6) except for the addition of two quadratic terms in ![]() $\tilde {\omega }_{e\|}$, and the absence of the linear terms
$\tilde {\omega }_{e\|}$, and the absence of the linear terms ![]() $\tilde {\omega }_{e\|} (\boldsymbol{\mathsf{M}}_{s}^{(0)})_{11}$ and
$\tilde {\omega }_{e\|} (\boldsymbol{\mathsf{M}}_{s}^{(0)})_{11}$ and ![]() $(\boldsymbol{\mathsf{P}}_{s}^{(0)})_{12}$. This motivates our approach to finding modes at arbitrary wavevectors: we solve a quartic dispersion relation that includes all the terms in (K22) and also those linear terms which were present in (K6), but absent in (K22). Explicitly, this dispersion relation is
$(\boldsymbol{\mathsf{P}}_{s}^{(0)})_{12}$. This motivates our approach to finding modes at arbitrary wavevectors: we solve a quartic dispersion relation that includes all the terms in (K22) and also those linear terms which were present in (K6), but absent in (K22). Explicitly, this dispersion relation is
 \begin{align} & \left\{-\tilde{\omega}_{e\|}^2 \left[\tfrac{4}{3} W_e + \tfrac{4}{3} W_i + \tfrac{1}{4} \left(L_e + L_i\right)^2\right] + \mathrm{i} \tilde{\omega}_{e\|} \left( F_e + \mu_e^{1/2} F_i \right) + \epsilon_e \left( W_e + \mu_e^{1/2} W_i \right)- k_{\|}^2 d_e^2\right\} \nonumber\\ & \quad \times \left[-\tilde{\omega}_{e\|}^2 \left(\tfrac{4}{3} {Y}_i + \tfrac{4}{3} {Y}_e \right)+ \mathrm{i} \tilde{\omega}_{e\|} \left( H_e + \mu_e^{1/2} H_i \right) + \epsilon_e \left( {Y}_e + \mu_e^{1/2} {Y}_i \right)- k^2 d_e^2\right] \nonumber\\ & \quad +\left[\mathrm{i} \tilde{\omega}_{e\|} \left( G_e + \mu_e^{1/2} G_i \right) + \epsilon_e \left( X_e + \mu_e^{1/2} X_i \right) \right]^2 = 0 , \end{align}
\begin{align} & \left\{-\tilde{\omega}_{e\|}^2 \left[\tfrac{4}{3} W_e + \tfrac{4}{3} W_i + \tfrac{1}{4} \left(L_e + L_i\right)^2\right] + \mathrm{i} \tilde{\omega}_{e\|} \left( F_e + \mu_e^{1/2} F_i \right) + \epsilon_e \left( W_e + \mu_e^{1/2} W_i \right)- k_{\|}^2 d_e^2\right\} \nonumber\\ & \quad \times \left[-\tilde{\omega}_{e\|}^2 \left(\tfrac{4}{3} {Y}_i + \tfrac{4}{3} {Y}_e \right)+ \mathrm{i} \tilde{\omega}_{e\|} \left( H_e + \mu_e^{1/2} H_i \right) + \epsilon_e \left( {Y}_e + \mu_e^{1/2} {Y}_i \right)- k^2 d_e^2\right] \nonumber\\ & \quad +\left[\mathrm{i} \tilde{\omega}_{e\|} \left( G_e + \mu_e^{1/2} G_i \right) + \epsilon_e \left( X_e + \mu_e^{1/2} X_i \right) \right]^2 = 0 , \end{align}
where ![]() $L_s \equiv L(k_{\|} \tilde {\rho }_s,k_{\bot } \tilde {\rho }_s)$. The special functions
$L_s \equiv L(k_{\|} \tilde {\rho }_s,k_{\bot } \tilde {\rho }_s)$. The special functions ![]() $W(x,y)$ and
$W(x,y)$ and ![]() ${Y}(x,y)$, defined in (G97), appear due to their relationship to the matrix
${Y}(x,y)$, defined in (G97), appear due to their relationship to the matrix ![]() $(\boldsymbol{\mathsf{M}}_{s}^{(1)})$ (derived in Appendix G.1.2)
$(\boldsymbol{\mathsf{M}}_{s}^{(1)})$ (derived in Appendix G.1.2)
combined with the identity
 \begin{equation} (\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} - \frac{(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}^2}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} ={-} \frac{k^2}{k_{\|}^2} \left[\frac{4}{3} W_e + \frac{4}{3} W_i + \frac{1}{4} \left(L_e + L_i\right)^2 \right] , \end{equation}
\begin{equation} (\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{11} - \frac{(\boldsymbol{\mathsf{M}}_{e}^{(1)} + \boldsymbol{\mathsf{M}}_{i}^{(1)})_{13}^2}{2 (\boldsymbol{\mathsf{M}}_{e}^{(1)})_{33}} ={-} \frac{k^2}{k_{\|}^2} \left[\frac{4}{3} W_e + \frac{4}{3} W_i + \frac{1}{4} \left(L_e + L_i\right)^2 \right] , \end{equation}proven in Appendix G.1.7.
The dispersion relation (K23) recovers all the roots of interest because it captures approximate values for all of the roots of the dispersion relations (K7) and (K22) in their respective wavenumber regions of validity. We note that, in situations when there are fewer than four physical modes (e.g. in the ![]() $k_{\|} \rho _e \gtrsim 1$ regime), solving (K23) will also return non-physical modes that are the result of the addition of higher-order terms in a regime where such terms are illegitimate. However, by construction, such modes can be distinguished by their large magnitude (
$k_{\|} \rho _e \gtrsim 1$ regime), solving (K23) will also return non-physical modes that are the result of the addition of higher-order terms in a regime where such terms are illegitimate. However, by construction, such modes can be distinguished by their large magnitude (![]() $\tilde {\omega }_{e\|} \sim 1$) as compared with the others. We acknowledge that our approach does not maintain consistent orderings: indeed, depending on the scale of a particular instability, there may be terms retained that are, in fact, smaller than other terms we have neglected when carrying out the
$\tilde {\omega }_{e\|} \sim 1$) as compared with the others. We acknowledge that our approach does not maintain consistent orderings: indeed, depending on the scale of a particular instability, there may be terms retained that are, in fact, smaller than other terms we have neglected when carrying out the ![]() $\tilde {\omega }_{i\|} \ll 1$ expansion. However, unlike the quadratic dispersion relation (K7), the quartic dispersion relation (K23) always captures the leading-order terms for arbitrary wavevectors, and so provides reasonable approximations to the complex frequency of all possible CES microinstabilities.
$\tilde {\omega }_{i\|} \ll 1$ expansion. However, unlike the quadratic dispersion relation (K7), the quartic dispersion relation (K23) always captures the leading-order terms for arbitrary wavevectors, and so provides reasonable approximations to the complex frequency of all possible CES microinstabilities.
K.3.2. Derivation of frequency and growth rate of the CES mirror instability
To derive the CES mirror instability's growth rate when it is close to marginality, we consider the dispersion relation (K23) under the orderings (4.6a,b), viz.
where ![]() $\varGamma _i = \Delta \beta _i-1$, and
$\varGamma _i = \Delta \beta _i-1$, and ![]() $\varDelta = \varDelta _i + \varDelta _e = 3(\epsilon _i+\epsilon _e)/2$. Using the asymptotic identities (G37) for the special functions
$\varDelta = \varDelta _i + \varDelta _e = 3(\epsilon _i+\epsilon _e)/2$. Using the asymptotic identities (G37) for the special functions ![]() $F_s$,
$F_s$, ![]() $G_s$,
$G_s$, ![]() $H_s$,
$H_s$, ![]() $L_s$ and
$L_s$ and ![]() $N_s$ and (G101) for
$N_s$ and (G101) for ![]() $W_s$,
$W_s$, ![]() $X_s$ and
$X_s$ and ![]() ${Y}_s$, (K23) becomes, after dropping terms that are asymptotically small under the ordering (K26a,b),
${Y}_s$, (K23) becomes, after dropping terms that are asymptotically small under the ordering (K26a,b),
which in turn can be rearranged to give (4.7) in § 4.3.1 and the subsequent results. We note that, save for the term ![]() $\propto G_e$, which cancels to leading order with its ion equivalent, and the term
$\propto G_e$, which cancels to leading order with its ion equivalent, and the term ![]() $\propto {Y}_e$, which we retain in order to capture correctly the mirror instability's exact stability threshold, the electron terms in (K23) are negligibly small under the ordering (K26a,b). We also observe that by assuming frequency ordering (K26a,b), we have removed the shear-Alfvén wave from the dispersion relation. As we demonstrate when characterising the growth rate of firehose-unstable shear-Alfvén waves (see § 4.4.3 and Appendix K.3.7), a different ordering is required to extract this mode (which is, in any case, stable for
$\propto {Y}_e$, which we retain in order to capture correctly the mirror instability's exact stability threshold, the electron terms in (K23) are negligibly small under the ordering (K26a,b). We also observe that by assuming frequency ordering (K26a,b), we have removed the shear-Alfvén wave from the dispersion relation. As we demonstrate when characterising the growth rate of firehose-unstable shear-Alfvén waves (see § 4.4.3 and Appendix K.3.7), a different ordering is required to extract this mode (which is, in any case, stable for ![]() $\varDelta _i > 0$).
$\varDelta _i > 0$).
To derive the growth rate of long-wavelength (![]() $k_{\|} \rho _i \sim k_{\perp } \rho _i \ll 1$) mirror modes away from marginality, when
$k_{\|} \rho _i \sim k_{\perp } \rho _i \ll 1$) mirror modes away from marginality, when ![]() $\varGamma _i \gtrsim 1$, we adopt the alternative ordering (4.9a,b), which is equivalent to
$\varGamma _i \gtrsim 1$, we adopt the alternative ordering (4.9a,b), which is equivalent to
Again using the identities (G37) and (G101) to evaludate the special functions, the dispersion relation (K23) is then
which, after some algebraic manipulation, gives (4.11) in § 4.3.1 and the subsequent results.
Finally, the expression (4.16) for the growth rate of sub-ion-Larmor scale mirror modes is derived by adopting the orderings (4.14a,b):
 \begin{equation} k_{\|} \rho_i \sim k_{{\perp}} \rho_i \sim (\varDelta_i \beta_i)^{1/2} \gg 1 , \quad \tilde{\omega}_{i\|} \sim \frac{\varDelta_i^{1/2}}{\beta_i^{1/2}} , \end{equation}
\begin{equation} k_{\|} \rho_i \sim k_{{\perp}} \rho_i \sim (\varDelta_i \beta_i)^{1/2} \gg 1 , \quad \tilde{\omega}_{i\|} \sim \frac{\varDelta_i^{1/2}}{\beta_i^{1/2}} , \end{equation}
and then using the asymptotic identities (G35) for evaluating ![]() $F_i$,
$F_i$, ![]() $G_i$,
$G_i$, ![]() $H_i$,
$H_i$, ![]() $L_i$ and
$L_i$ and ![]() $N_i$, (G37) for
$N_i$, (G37) for ![]() $F_e$,
$F_e$, ![]() $G_e$,
$G_e$, ![]() $H_e$,
$H_e$, ![]() $L_e$ and
$L_e$ and ![]() $N_e$, (G99) for
$N_e$, (G99) for ![]() $W_i$,
$W_i$, ![]() $X_i$ and
$X_i$ and ![]() ${Y}_i$ and (G101) for
${Y}_i$ and (G101) for ![]() $W_e$,
$W_e$, ![]() $X_e$ and
$X_e$ and ![]() ${Y}_e$. Once again neglecting small terms under the assumed ordering, the dispersion relation (K23) simplifies to a quadratic of the form (K6):
${Y}_e$. Once again neglecting small terms under the assumed ordering, the dispersion relation (K23) simplifies to a quadratic of the form (K6):
 \begin{equation} \left[-\frac{\varDelta_i}{2} \frac{2 k_{\|}^2 \left(k_{\|}^2- k_{\bot}^2\right)}{k^4} + \frac{k_{\|}^2 \rho_i^2}{\beta_i}\right] \left(-\varDelta_i \frac{k_{\|}^2}{k^2}+ \frac{k^2 \rho_i^2}{\beta_i}\right) -\tilde{\omega}_{i\|}^2 k_{\|}^2 \rho_i^2 = 0 \, , \end{equation}
\begin{equation} \left[-\frac{\varDelta_i}{2} \frac{2 k_{\|}^2 \left(k_{\|}^2- k_{\bot}^2\right)}{k^4} + \frac{k_{\|}^2 \rho_i^2}{\beta_i}\right] \left(-\varDelta_i \frac{k_{\|}^2}{k^2}+ \frac{k^2 \rho_i^2}{\beta_i}\right) -\tilde{\omega}_{i\|}^2 k_{\|}^2 \rho_i^2 = 0 \, , \end{equation}from which follow (4.16) and the subsequent results in § 4.3.1.
K.3.3. Derivation of frequency and growth rate of the parallel CES whistler instability
We derive the expressions (4.21) for the real frequency and growth rate of the parallel CES whistler instability by adopting the ordering (4.20a,b)
and evaluating ![]() $F_s$,
$F_s$, ![]() $G_s$,
$G_s$, ![]() $H_s$,
$H_s$, ![]() $L_s$ and
$L_s$ and ![]() $N_s$ via (G34), and
$N_s$ via (G34), and ![]() $W_s$,
$W_s$, ![]() $X_s$ and
$X_s$ and ![]() ${Y}_s$ via (G98). The special functions with
${Y}_s$ via (G98). The special functions with ![]() $s = i$ are simplified further by assuming additionally that
$s = i$ are simplified further by assuming additionally that ![]() $k_{\|} \rho _i \gg 1$. Under these assumptions and simplifications, the dispersion relation (K23) becomes
$k_{\|} \rho _i \gg 1$. Under these assumptions and simplifications, the dispersion relation (K23) becomes
 \begin{align} &\left\{\mathrm{i} \tilde{\omega}_{e\|} \sqrt{\rm \pi} \left[\exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} + \mu_e^{1/2} \right] +\varDelta_e \left[1+\frac{1}{k_{\|} \rho_e} {\rm Re}{\,Z\!\left(\frac{1}{k_{\|} \rho_e}\right)} + \mu_e^{1/2}\right] - \frac{k_\|^2 \rho_e^2}{\beta_e}\right\}^2 \nonumber\\ &\quad +\left\{\mathrm{i} \tilde{\omega}_{e\|} {\rm Re}{\,Z\!\left(\frac{1}{k_{\|} \rho_e}\right)} - \frac{\varDelta_e}{k_\| \rho_e} \left[\sqrt{\rm \pi} \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} + \mu_e \right] \right\}^2 = 0 , \end{align}
\begin{align} &\left\{\mathrm{i} \tilde{\omega}_{e\|} \sqrt{\rm \pi} \left[\exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} + \mu_e^{1/2} \right] +\varDelta_e \left[1+\frac{1}{k_{\|} \rho_e} {\rm Re}{\,Z\!\left(\frac{1}{k_{\|} \rho_e}\right)} + \mu_e^{1/2}\right] - \frac{k_\|^2 \rho_e^2}{\beta_e}\right\}^2 \nonumber\\ &\quad +\left\{\mathrm{i} \tilde{\omega}_{e\|} {\rm Re}{\,Z\!\left(\frac{1}{k_{\|} \rho_e}\right)} - \frac{\varDelta_e}{k_\| \rho_e} \left[\sqrt{\rm \pi} \exp{\left(-\frac{1}{k_\|^2 \rho_e^2}\right)} + \mu_e \right] \right\}^2 = 0 , \end{align}
where we have substituted ![]() $\tilde {\rho }_e = - \rho _e$, and the only ion terms that we retain – the terms proportional to
$\tilde {\rho }_e = - \rho _e$, and the only ion terms that we retain – the terms proportional to ![]() $\mu _e^{1/2}$ or
$\mu _e^{1/2}$ or ![]() $\mu _e$ – are those that we find to affect the dispersion relation qualitatively (as explained in the main text, these terms are formally small under the assumed ordering, but cannot be neglected in certain subsidiary limits, e.g.
$\mu _e$ – are those that we find to affect the dispersion relation qualitatively (as explained in the main text, these terms are formally small under the assumed ordering, but cannot be neglected in certain subsidiary limits, e.g. ![]() $k_{\|} \rho _e \ll 1$, which we will subsequently wish to explore). (K33) can then be factorised to give two complex roots, the real and imaginary parts of which become (4.21a) and (4.21b), respectively.
$k_{\|} \rho _e \ll 1$, which we will subsequently wish to explore). (K33) can then be factorised to give two complex roots, the real and imaginary parts of which become (4.21a) and (4.21b), respectively.
K.3.4. Derivation of frequency and growth rate of the CES transverse instability
To obtain the growth rate (4.29b) of the two CES transverse modes, we take directly the unmagnetised limit of the full CES dispersion relation (K23) under the orderings
and then employ asymptotic identities (G35) for ![]() $F_s$,
$F_s$, ![]() $G_s$,
$G_s$, ![]() $H_s$,
$H_s$, ![]() $L_s$ and
$L_s$ and ![]() $N_s$, and (G99) for
$N_s$, and (G99) for ![]() $W_s$,
$W_s$, ![]() $X_s$ and
$X_s$ and ![]() ${Y}_s$. We then obtain a dispersion relation similar to (K6), but with two separable roots:
${Y}_s$. We then obtain a dispersion relation similar to (K6), but with two separable roots:
 \begin{equation} \left[\mathrm{i} \tilde{\omega}_{e\|} \sqrt{\rm \pi} \frac{k_{\|}^3}{k^3} +\varDelta_e \frac{k_{\|}^2 (k_{\|}^2- k_{\bot}^2)}{k^4} - \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right] \left(\mathrm{i} \tilde{\omega}_{e\|} \sqrt{\rm \pi} \frac{k_{\|}}{k} +\varDelta_e \frac{k_{\|}^2}{k^2} - \frac{k^2 \rho_e^2}{\beta_e}\right) = 0 . \end{equation}
\begin{equation} \left[\mathrm{i} \tilde{\omega}_{e\|} \sqrt{\rm \pi} \frac{k_{\|}^3}{k^3} +\varDelta_e \frac{k_{\|}^2 (k_{\|}^2- k_{\bot}^2)}{k^4} - \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right] \left(\mathrm{i} \tilde{\omega}_{e\|} \sqrt{\rm \pi} \frac{k_{\|}}{k} +\varDelta_e \frac{k_{\|}^2}{k^2} - \frac{k^2 \rho_e^2}{\beta_e}\right) = 0 . \end{equation}When rearranged, the first bracket gives expression (4.29a), and the second bracket gives (4.29b).
K.3.5. Derivation of frequency and growth rate of the CES electron mirror instability
When its marginality parameter ![]() $\varGamma _e = \varDelta _e \beta _e -1$ is small, the growth rate (4.35) (and zero real frequency) of the CES electron mirror instability's can be derived from the dispersion relation (K23) by adopting the ordering (4.34), viz.
$\varGamma _e = \varDelta _e \beta _e -1$ is small, the growth rate (4.35) (and zero real frequency) of the CES electron mirror instability's can be derived from the dispersion relation (K23) by adopting the ordering (4.34), viz.
and assuming that ![]() $\varGamma _e \gg \mu _e^{1/2}$. This latter inequality implies that
$\varGamma _e \gg \mu _e^{1/2}$. This latter inequality implies that ![]() $1 \ll k_{\|} \rho _i \ll k_{\perp } \rho _i$, so we use the asymptotic identities (G35) to simplify
$1 \ll k_{\|} \rho _i \ll k_{\perp } \rho _i$, so we use the asymptotic identities (G35) to simplify ![]() $F_i$,
$F_i$, ![]() $G_i$,
$G_i$, ![]() $H_i$,
$H_i$, ![]() $L_i$ and
$L_i$ and ![]() $N_i$, (G99) to simplify
$N_i$, (G99) to simplify ![]() $W_i$,
$W_i$, ![]() $X_i$ and
$X_i$ and ![]() ${Y}_i$, (G37) for
${Y}_i$, (G37) for ![]() $F_e$,
$F_e$, ![]() $G_e$,
$G_e$, ![]() $H_e$,
$H_e$, ![]() $L_e$ and
$L_e$ and ![]() $N_e$, and (G101) for
$N_e$, and (G101) for ![]() $W_e$,
$W_e$, ![]() $X_e$ and
$X_e$ and ![]() ${Y}_e$. Collecting terms, using the identity
${Y}_e$. Collecting terms, using the identity ![]() $\varDelta _e = (1+\varGamma _e)/\beta _e$, and keeping only leading-order ones, the dispersion relation simplifies to
$\varDelta _e = (1+\varGamma _e)/\beta _e$, and keeping only leading-order ones, the dispersion relation simplifies to
Because the discriminant of the quadratic (K37) is negative, it follows that its solution satisfies ![]() $\omega = \mathrm {i} \gamma$, with
$\omega = \mathrm {i} \gamma$, with ![]() $\gamma$ being given by (4.35).
$\gamma$ being given by (4.35).
To derive the expression (4.39) for the complex frequency of long-wavelength electron mirror modes, we adopt the ordering (4.38),
and then consider the subsidiary limit ![]() $k_{\|} \rho _e \sim k_{\perp } \rho _e \sim \mu _e^{1/4} \ll 1$ of the dispersion relation (K23). Using the asymptotic identities (G35) for
$k_{\|} \rho _e \sim k_{\perp } \rho _e \sim \mu _e^{1/4} \ll 1$ of the dispersion relation (K23). Using the asymptotic identities (G35) for ![]() $F_i$,
$F_i$, ![]() $G_i$,
$G_i$, ![]() $H_i$,
$H_i$, ![]() $L_i$ and
$L_i$ and ![]() $N_i$, (G37) for
$N_i$, (G37) for ![]() $F_e$,
$F_e$, ![]() $G_e$,
$G_e$, ![]() $H_e$,
$H_e$, ![]() $L_e$ and
$L_e$ and ![]() $N_e$, (G99) for
$N_e$, (G99) for ![]() $W_i$,
$W_i$, ![]() $X_i$ and
$X_i$ and ![]() ${Y}_i$ and (G101) for
${Y}_i$ and (G101) for ![]() $W_e$,
$W_e$, ![]() $X_e$ and
$X_e$ and ![]() ${Y}_e$, we find that
${Y}_e$, we find that
 \begin{align} & \left\{\frac{\varDelta_e}{2} \left[ k_{\|}^2 \rho_e^2 - \mu_e^{1/2} \frac{2 k_{\|}^2 \left(k_{\|}^2- k_{\bot}^2\right)}{k^4} \right]+ \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right\} \nonumber\\ & \quad \times \left[ \frac{\varDelta_e}{2} \left( k_{\|}^2 \rho_e^2 - 2 k_{\bot}^2 \rho_e^2 - \mu_e^{1/2} \frac{2 k_{\|}^2}{k^2} \right)+ \frac{k^2 \rho_e^2}{\beta_e}\right] -\tilde{\omega}_{e\|}^2 k_{\|}^2 \rho_e^2 = 0 , \end{align}
\begin{align} & \left\{\frac{\varDelta_e}{2} \left[ k_{\|}^2 \rho_e^2 - \mu_e^{1/2} \frac{2 k_{\|}^2 \left(k_{\|}^2- k_{\bot}^2\right)}{k^4} \right]+ \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right\} \nonumber\\ & \quad \times \left[ \frac{\varDelta_e}{2} \left( k_{\|}^2 \rho_e^2 - 2 k_{\bot}^2 \rho_e^2 - \mu_e^{1/2} \frac{2 k_{\|}^2}{k^2} \right)+ \frac{k^2 \rho_e^2}{\beta_e}\right] -\tilde{\omega}_{e\|}^2 k_{\|}^2 \rho_e^2 = 0 , \end{align}
where both the CE ion- and electron-shear terms are kept on account of their equal size under the assumed ordering. Solving for ![]() $\omega$ gives (4.39).
$\omega$ gives (4.39).
K.3.6. Derivation of frequency and growth rate of the parallel CES firehose instability
The relevant orderings of parameters to adopt in order to derive the complex frequency (4.47) of the parallel CES firehose instability is (4.45), viz.
with an additional small wavenumber-angle condition ![]() $k_{\bot } \rho _i \ll \beta _i^{-3/4}$ (which we shall justify a posteriori). Under this ordering, the special functions
$k_{\bot } \rho _i \ll \beta _i^{-3/4}$ (which we shall justify a posteriori). Under this ordering, the special functions ![]() $F_s$,
$F_s$, ![]() $G_s$,
$G_s$, ![]() $H_s$,
$H_s$, ![]() $L_s$ and
$L_s$ and ![]() $N_s$ can be simplified using (G37), and
$N_s$ can be simplified using (G37), and ![]() $W_s$,
$W_s$, ![]() $X_s$ and
$X_s$ and ![]() ${Y}_s$ using (G101), and so the dispersion relation (K23) reduces to
${Y}_s$ using (G101), and so the dispersion relation (K23) reduces to
 \begin{equation} \left(\tilde{\omega}_{i\|}^2 - \frac{\varDelta_i}{2} - \frac{1}{\beta_i}\right)^2 - \frac{\tilde{\omega}_{i\|}^2}{4} k_{\|}^2 \rho_i^2 = 0 , \end{equation}
\begin{equation} \left(\tilde{\omega}_{i\|}^2 - \frac{\varDelta_i}{2} - \frac{1}{\beta_i}\right)^2 - \frac{\tilde{\omega}_{i\|}^2}{4} k_{\|}^2 \rho_i^2 = 0 , \end{equation}
where the only non-negligible electron term is the one ![]() $\propto \tilde {\omega }_{e\|} G_e$. Similarly to the CES mirror instability (see Appendix K.3.2), this term cancels to leading order with its ion equivalent, and the next-order electron term is much smaller than the equivalent ion term. This dispersion relation can be rearranged to give (4.47).
$\propto \tilde {\omega }_{e\|} G_e$. Similarly to the CES mirror instability (see Appendix K.3.2), this term cancels to leading order with its ion equivalent, and the next-order electron term is much smaller than the equivalent ion term. This dispersion relation can be rearranged to give (4.47).
We also note that, in deriving (K41) from (K23), we have assumed that the linear term ![]() $\propto \tilde {\omega }_{e\|} \mu _e^{1/2} H_i$ is much smaller than the quadratic term
$\propto \tilde {\omega }_{e\|} \mu _e^{1/2} H_i$ is much smaller than the quadratic term ![]() $\propto \tilde {\omega }_{e\|}^2 {Y}_i$; their relative magnitude is given by
$\propto \tilde {\omega }_{e\|}^2 {Y}_i$; their relative magnitude is given by
 \begin{equation} \frac{\tilde{\omega}_{e\|} \mu_e^{1/2} H_i}{\tilde{\omega}_{e\|}^2 {Y}_i} \sim \frac{k_{\bot}^2 \rho_i^2}{ \tilde{\omega}_{i\|} k_{\|}^2 \rho_i^2} \sim \beta_i^{3/2} k_{\bot}^2 \rho_i^2 . \end{equation}
\begin{equation} \frac{\tilde{\omega}_{e\|} \mu_e^{1/2} H_i}{\tilde{\omega}_{e\|}^2 {Y}_i} \sim \frac{k_{\bot}^2 \rho_i^2}{ \tilde{\omega}_{i\|} k_{\|}^2 \rho_i^2} \sim \beta_i^{3/2} k_{\bot}^2 \rho_i^2 . \end{equation}
Thus, this assumption (which it is necessary to make in order for there to be both left-handed and right-handed Alfvén modes in high-![]() $\beta$ plasma) is only justified if the small-angle condition
$\beta$ plasma) is only justified if the small-angle condition ![]() $k_{\bot } \rho _i \ll \beta _i^{-3/4} \ll 1$ holds true.
$k_{\bot } \rho _i \ll \beta _i^{-3/4} \ll 1$ holds true.
K.3.7. Derivation of frequency and growth rate of the oblique CES firehose instability
To derive the oblique firehose's growth rate (4.52), we use the ordering (4.51), viz.
Simplifying the special functions ![]() $F_s$,
$F_s$, ![]() $G_s$,
$G_s$, ![]() $H_s$,
$H_s$, ![]() $L_s$ and
$L_s$ and ![]() $N_s$ via (G37), and
$N_s$ via (G37), and ![]() $W_s$,
$W_s$, ![]() $X_s$ and
$X_s$ and ![]() ${Y}_s$ via (G101), the dispersion relation (K23) becomes
${Y}_s$ via (G101), the dispersion relation (K23) becomes
 \begin{equation} \mathrm{i} \sqrt{\rm \pi} \left(\tilde{\omega}_{i\|}^2 - \frac{\varDelta_i}{2} - \frac{1}{\beta_i}\right) k_{\bot}^2 \rho_i^2 \tilde{\omega}_{i\|} - \frac{\tilde{\omega}_{i\|}^2}{4} \left(k_{\|}^2 \rho_i^2 - \frac{3}{2} k_{\bot}^2 \rho_i^2 \right)^2 = 0 , \end{equation}
\begin{equation} \mathrm{i} \sqrt{\rm \pi} \left(\tilde{\omega}_{i\|}^2 - \frac{\varDelta_i}{2} - \frac{1}{\beta_i}\right) k_{\bot}^2 \rho_i^2 \tilde{\omega}_{i\|} - \frac{\tilde{\omega}_{i\|}^2}{4} \left(k_{\|}^2 \rho_i^2 - \frac{3}{2} k_{\bot}^2 \rho_i^2 \right)^2 = 0 , \end{equation}
where, in contrast to the quasi-parallel firehose, the linear term ![]() $\propto \tilde {\omega }_{e\|} \mu _e^{1/2} H_i$ in (K23) is larger than the quadratic term
$\propto \tilde {\omega }_{e\|} \mu _e^{1/2} H_i$ in (K23) is larger than the quadratic term ![]() $\propto \tilde {\omega }_{e\|}^2 {Y}_i$. (K44) can be solved to give two roots:
$\propto \tilde {\omega }_{e\|}^2 {Y}_i$. (K44) can be solved to give two roots: ![]() $\omega \approx 0$, corresponding to the stable slow mode (whose damping rate is asymptotically small under the assumed ordering), and the expression (4.52) for the complex frequency of the (sometimes firehose-unstable) shear-Alfvén mode.
$\omega \approx 0$, corresponding to the stable slow mode (whose damping rate is asymptotically small under the assumed ordering), and the expression (4.52) for the complex frequency of the (sometimes firehose-unstable) shear-Alfvén mode.
K.3.8. Derivation of frequency and growth rate of the critical-line CES firehose instability
To characterise the growth of the critical-line firehose when ![]() $\beta _i \gg 10^{6}$, we set
$\beta _i \gg 10^{6}$, we set ![]() $k_\perp = 2 k_{\|}/3$, and order
$k_\perp = 2 k_{\|}/3$, and order
 \begin{equation} \tilde{\omega}_{i\|} \sim \beta_i^{{-}3/5} \sim k_{\|}^6 \rho_i^6 \sim \left|\varDelta_i + \frac{2}{\beta_i}\right|^{1/2} . \end{equation}
\begin{equation} \tilde{\omega}_{i\|} \sim \beta_i^{{-}3/5} \sim k_{\|}^6 \rho_i^6 \sim \left|\varDelta_i + \frac{2}{\beta_i}\right|^{1/2} . \end{equation}
The dispersion relation (K23) transforms similarly to (K44) in this case, with two important exceptions: first, the term in (K23) ![]() $\propto \tilde {\omega }_{e\|} G_e + \mu _e^{1/2} \tilde {\omega }_{e\|} G_i$ is
$\propto \tilde {\omega }_{e\|} G_e + \mu _e^{1/2} \tilde {\omega }_{e\|} G_i$ is ![]() ${O}(k_\|^5 \rho _i^5)$ on the critical line, rather than
${O}(k_\|^5 \rho _i^5)$ on the critical line, rather than ![]() ${O}(k_{\|}^3 \rho _i^3)$; secondly, our choice of ordering requires that we retain
${O}(k_{\|}^3 \rho _i^3)$; secondly, our choice of ordering requires that we retain ![]() ${O}(k_\|^4 \rho _i^4)$. This gives
${O}(k_\|^4 \rho _i^4)$. This gives
To obtain the expression (4.57) for the critical-line firehose's growth rate in the limit ![]() $\beta _i \gg 10^6$ that is valid under the ordering (4.56), we consider the subsidiary limit
$\beta _i \gg 10^6$ that is valid under the ordering (4.56), we consider the subsidiary limit
in which case (K46) becomes
The expression (4.57) follows from solving (K48) for ![]() $\omega$ (and once again neglecting the
$\omega$ (and once again neglecting the ![]() $\omega \approx 0$ solution).
$\omega \approx 0$ solution).
The expression (4.61) for the growth of critical-line firehose modes when ![]() $\beta _i \simeq -2/\varDelta _i \gg 10^6$, can be deduced by considering the opposite subsidiary limit to (K47), viz.
$\beta _i \simeq -2/\varDelta _i \gg 10^6$, can be deduced by considering the opposite subsidiary limit to (K47), viz.
In this limit, (K46) simplifies to
Noting that the quadratic (K50) has a negative discriminant, we deduce that ![]() $\omega = \mathrm {i} \gamma$; then solving (K50) for
$\omega = \mathrm {i} \gamma$; then solving (K50) for ![]() $\gamma$ gives (4.61).
$\gamma$ gives (4.61).
When ![]() $\beta _i \ll 10^6$, the appropriate ordering to adopt in order to simplify the dispersion relation of critical-line is no longer (K51a,b), but instead
$\beta _i \ll 10^6$, the appropriate ordering to adopt in order to simplify the dispersion relation of critical-line is no longer (K51a,b), but instead
 \begin{equation} \tilde{\omega}_{i\|} \sim \frac{1}{\sqrt{\beta_i \log{\beta_i}}} \sim \left|\varDelta_i + \frac{2}{\beta_i}\right|^{1/2} , \quad k_{\|} \rho_i \sim \frac{1}{\sqrt{\log{\beta_i}}} . \end{equation}
\begin{equation} \tilde{\omega}_{i\|} \sim \frac{1}{\sqrt{\beta_i \log{\beta_i}}} \sim \left|\varDelta_i + \frac{2}{\beta_i}\right|^{1/2} , \quad k_{\|} \rho_i \sim \frac{1}{\sqrt{\log{\beta_i}}} . \end{equation}
Under this ordering, the term ![]() $\propto \mu _e^{1/2} \tilde {\omega }_{e\|} F_i$ in (K23) is retained, while the term
$\propto \mu _e^{1/2} \tilde {\omega }_{e\|} F_i$ in (K23) is retained, while the term ![]() $\propto \tilde {\omega }_{e\|} G_e + \mu _e^{1/2} \tilde {\omega }_{e\|} G_i$ is neglected. This gives
$\propto \tilde {\omega }_{e\|} G_e + \mu _e^{1/2} \tilde {\omega }_{e\|} G_i$ is neglected. This gives
 \begin{equation} \left[\tilde{\omega}_{i\|}^2 + \mathrm{i} \frac{\sqrt{\rm \pi}}{k_{\|}^2 \rho_i^2} \exp{\left(-\frac{1}{k_{\|}^2 \rho_i^2}\right)} \tilde{\omega}_{i\|} - \frac{1}{2} \varDelta_i- \frac{1}{\beta_i} - \frac{5}{8} \varDelta_i k_{\|}^{2} \rho_i^{2}\right] \tilde{\omega}_{i\|} = 0 . \end{equation}
\begin{equation} \left[\tilde{\omega}_{i\|}^2 + \mathrm{i} \frac{\sqrt{\rm \pi}}{k_{\|}^2 \rho_i^2} \exp{\left(-\frac{1}{k_{\|}^2 \rho_i^2}\right)} \tilde{\omega}_{i\|} - \frac{1}{2} \varDelta_i- \frac{1}{\beta_i} - \frac{5}{8} \varDelta_i k_{\|}^{2} \rho_i^{2}\right] \tilde{\omega}_{i\|} = 0 . \end{equation} To obtain the expression (4.65) for the critical-line firehose instability's growth rate in the case when ordering (4.64a,b) holds – that is, when ![]() $\varDelta _i \beta _i +2| \sim 1$, we consider the appropriate subsidiary limit of (K52)
$\varDelta _i \beta _i +2| \sim 1$, we consider the appropriate subsidiary limit of (K52)
In this case, the last term in the square brackets on the left-hand side of (K52) can be neglected, leaving the only non-trivial roots to satisfy
 \begin{equation} \tilde{\omega}_{i\|}^2 + \mathrm{i} \frac{\sqrt{\rm \pi}}{k_{\|}^2 \rho_i^2} \exp{\left(-\frac{1}{k_{\|}^2 \rho_i^2}\right)} \tilde{\omega}_{i\|} - \frac{\varDelta_i}{2} - \frac{1}{\beta_i} = 0 , \end{equation}
\begin{equation} \tilde{\omega}_{i\|}^2 + \mathrm{i} \frac{\sqrt{\rm \pi}}{k_{\|}^2 \rho_i^2} \exp{\left(-\frac{1}{k_{\|}^2 \rho_i^2}\right)} \tilde{\omega}_{i\|} - \frac{\varDelta_i}{2} - \frac{1}{\beta_i} = 0 , \end{equation}
whence (4.65) follows immediately. The case of growth when ![]() $\varDelta _i \simeq -2/\beta _i$ can be recovered from the opposite subsidiary limit
$\varDelta _i \simeq -2/\beta _i$ can be recovered from the opposite subsidiary limit
In this case, the dispersion relation of the critical-line firehose modes is
 \begin{equation} \tilde{\omega}_{i\|}^2 + \mathrm{i} \frac{\sqrt{\rm \pi}}{k_{\|}^2 \rho_i^2} \exp{\left(-\frac{1}{k_{\|}^2 \rho_i^2}\right)} \tilde{\omega}_{i\|} + \frac{5}{4 \beta_i} k_{\|}^2 \rho_i^2 = 0 , \end{equation}
\begin{equation} \tilde{\omega}_{i\|}^2 + \mathrm{i} \frac{\sqrt{\rm \pi}}{k_{\|}^2 \rho_i^2} \exp{\left(-\frac{1}{k_{\|}^2 \rho_i^2}\right)} \tilde{\omega}_{i\|} + \frac{5}{4 \beta_i} k_{\|}^2 \rho_i^2 = 0 , \end{equation}
which, when solved for the growth rate ![]() $\gamma = -{\rm i} \omega$, gives (4.68).
$\gamma = -{\rm i} \omega$, gives (4.68).
K.3.9. Derivation of frequency and growth rate of the CES parallel electron firehose instability
This derivation is identical to that given in Appendix K.3.3 for the frequency and growth rate of the parallel CES whistler instability, and the same expressions (4.21) are used in § 4.4.7.
K.3.10. Derivation of frequency and growth rate of the CES oblique electron firehose instability
The complex frequency (4.86) of the electron-firehose modes with ![]() $\mu _e^{1/2} \ll k_{\|} \rho _e \ll k_{\perp } \rho _e \sim 1$ is derived by applying the ordering
$\mu _e^{1/2} \ll k_{\|} \rho _e \ll k_{\perp } \rho _e \sim 1$ is derived by applying the ordering
to (K23) and using the asymptotic identities (G35) for ![]() $F_i$,
$F_i$, ![]() $G_i$,
$G_i$, ![]() $H_i$,
$H_i$, ![]() $L_i$ and
$L_i$ and ![]() $N_i$, (G36) for
$N_i$, (G36) for ![]() $F_e$,
$F_e$, ![]() $G_e$,
$G_e$, ![]() $H_e$,
$H_e$, ![]() $L_e$ and
$L_e$ and ![]() $N_e$, (G99) for
$N_e$, (G99) for ![]() $W_i$,
$W_i$, ![]() $X_i$ and
$X_i$ and ![]() ${Y}_i$ and (G100) for
${Y}_i$ and (G100) for ![]() $W_e$,
$W_e$, ![]() $X_e$ and
$X_e$ and ![]() ${Y}_e$. We obtain the simplified dispersion relation
${Y}_e$. We obtain the simplified dispersion relation
 \begin{align} & \left\{-\varDelta_e \frac{k_{\|}^2}{k_{\bot}^2} \left[1 - \exp \left(-\frac{k_{\bot}^2 \rho_e^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right)\right]- \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right\} \nonumber\\ & \quad \times \left\{\left(\mathrm{i} \sqrt{\rm \pi} \tilde{\omega}_{e\|} + \varDelta_e \right) k_{\bot}^2 \rho_e^2 \exp \left(-\frac{k_{\bot}^2 \rho_e^2}{2}\right) \left[{I}_0\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right) - {I}_1\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right) \right] - \frac{k^2 \rho_e^2}{\beta_e}\right\} \nonumber\\ & \quad - k_{\|}^2 \rho_e^2 \tilde{\omega}_{e\|}^2 \exp \left({-}k_{\bot}^2 \rho_e^2\right) \left[{I}_0\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right) - {I}_1\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right)\right]^2 = 0 . \end{align}
\begin{align} & \left\{-\varDelta_e \frac{k_{\|}^2}{k_{\bot}^2} \left[1 - \exp \left(-\frac{k_{\bot}^2 \rho_e^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right)\right]- \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right\} \nonumber\\ & \quad \times \left\{\left(\mathrm{i} \sqrt{\rm \pi} \tilde{\omega}_{e\|} + \varDelta_e \right) k_{\bot}^2 \rho_e^2 \exp \left(-\frac{k_{\bot}^2 \rho_e^2}{2}\right) \left[{I}_0\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right) - {I}_1\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right) \right] - \frac{k^2 \rho_e^2}{\beta_e}\right\} \nonumber\\ & \quad - k_{\|}^2 \rho_e^2 \tilde{\omega}_{e\|}^2 \exp \left({-}k_{\bot}^2 \rho_e^2\right) \left[{I}_0\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right) - {I}_1\!\left(\frac{k_{\bot}^2 \rho_e^2}{2}\right)\right]^2 = 0 . \end{align}
Introducing the special functions ![]() $\mathcal {F}(k_{\perp } \rho _e)$ and
$\mathcal {F}(k_{\perp } \rho _e)$ and ![]() $\mathcal {H}(k_{\perp } \rho _e)$ given by (4.89), and then rearranging (K58), leads to (4.86).
$\mathcal {H}(k_{\perp } \rho _e)$ given by (4.89), and then rearranging (K58), leads to (4.86).
K.3.11. Derivation of frequency and growth rate of the CES EST instability
To derive the expression (4.97) for the growth rate of the EST instability in the limits ![]() $\mu _e^{1/2} \ll k_{\|} \rho _e \ll 1 \ll k_{\bot } \rho _e \ll \beta _e^{1/7}$, and
$\mu _e^{1/2} \ll k_{\|} \rho _e \ll 1 \ll k_{\bot } \rho _e \ll \beta _e^{1/7}$, and ![]() $\varDelta _e \beta _e \gg 1$, we apply the orderings (4.96a–c), viz.
$\varDelta _e \beta _e \gg 1$, we apply the orderings (4.96a–c), viz.
to (K23). We then use the asymptotic identities (G35) for ![]() $F_i$,
$F_i$, ![]() $G_i$,
$G_i$, ![]() $H_i$,
$H_i$, ![]() $L_i$ and
$L_i$ and ![]() $N_i$, (G38) for
$N_i$, (G38) for ![]() $F_e$,
$F_e$, ![]() $G_e$,
$G_e$, ![]() $H_e$,
$H_e$, ![]() $L_e$ and
$L_e$ and ![]() $N_e$, (G99) for
$N_e$, (G99) for ![]() $W_i$,
$W_i$, ![]() $X_i$ and
$X_i$ and ![]() ${Y}_i$ and (G102) for
${Y}_i$ and (G102) for ![]() $W_e$,
$W_e$, ![]() $X_e$ and
$X_e$ and ![]() ${Y}_e$ to give
${Y}_e$ to give
 \begin{equation} \mathrm{i} \frac{\tilde{\omega}_{e\|}}{k_{\bot} \rho_e } \left\{\mathrm{i} \frac{\tilde{\omega}_{e\|}}{k_{\bot}^3 \rho_e^3} \left[4 \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} +\sqrt{\rm \pi} \mu_e^{1/2} k_{\|}^3 \rho_e^{3} \right]- \varDelta_e \frac{k_{\|}^2 \rho_e^2}{k_{\bot}^2 \rho_e^2} - \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right\} - \frac{k_{\|}^2 \rho_e^2 \tilde{\omega}_{e\|}^2}{{\rm \pi} k_{\bot}^6 \rho_i^6 } = 0 , \end{equation}
\begin{equation} \mathrm{i} \frac{\tilde{\omega}_{e\|}}{k_{\bot} \rho_e } \left\{\mathrm{i} \frac{\tilde{\omega}_{e\|}}{k_{\bot}^3 \rho_e^3} \left[4 \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} +\sqrt{\rm \pi} \mu_e^{1/2} k_{\|}^3 \rho_e^{3} \right]- \varDelta_e \frac{k_{\|}^2 \rho_e^2}{k_{\bot}^2 \rho_e^2} - \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right\} - \frac{k_{\|}^2 \rho_e^2 \tilde{\omega}_{e\|}^2}{{\rm \pi} k_{\bot}^6 \rho_i^6 } = 0 , \end{equation}
where the only ion contribution that is not always small, and thus cannot be neglected, is the term proportional to ![]() $\mu _e^{1/2}$. Solving for the frequency gives
$\mu _e^{1/2}$. Solving for the frequency gives ![]() $\omega \approx 0$ – corresponding to a damped mode whose frequency is asymptotically small under the assumed ordering (K59a–c) – and the EST mode, whose growth rate is given by (4.97).
$\omega \approx 0$ – corresponding to a damped mode whose frequency is asymptotically small under the assumed ordering (K59a–c) – and the EST mode, whose growth rate is given by (4.97).
K.3.12. Derivation of frequency and growth rate of the CES whisper instability
In the limits ![]() $\mu _e^{1/2} \ll k_{\|} \rho _e \ll 1 \gg k_{\bot } \rho _e$ and
$\mu _e^{1/2} \ll k_{\|} \rho _e \ll 1 \gg k_{\bot } \rho _e$ and ![]() $\varDelta _e \beta _e \gg 1$ under the orderings
$\varDelta _e \beta _e \gg 1$ under the orderings
the dispersion relation (K23) becomes
 \begin{equation} \mathrm{i} \frac{\tilde{\omega}_{e\|}}{k_{\bot} \rho_e } \left\{ \frac{k_{\|}^2 \rho_e^2}{k_{\bot}^2 \rho_e^2} \frac{4 \tilde{\omega}_{e\|}^2}{\sqrt{\rm \pi} k_{\bot} \rho_e} + \mathrm{i} \frac{4 \tilde{\omega}_{e\|}}{k_{\bot}^3 \rho_e^3} \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} - \varDelta_e \frac{k_{\|}^2 \rho_e^2}{k_{\bot}^2 \rho_e^2} - \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right\} - \frac{k_{\|}^2 \rho_e^2 \tilde{\omega}_{e\|}^2}{{\rm \pi} k_{\bot}^6 \rho_e^6 } = 0 , \quad \end{equation}
\begin{equation} \mathrm{i} \frac{\tilde{\omega}_{e\|}}{k_{\bot} \rho_e } \left\{ \frac{k_{\|}^2 \rho_e^2}{k_{\bot}^2 \rho_e^2} \frac{4 \tilde{\omega}_{e\|}^2}{\sqrt{\rm \pi} k_{\bot} \rho_e} + \mathrm{i} \frac{4 \tilde{\omega}_{e\|}}{k_{\bot}^3 \rho_e^3} \exp{\left(-\frac{1}{k_{\|}^2 \rho_e^2}\right)} - \varDelta_e \frac{k_{\|}^2 \rho_e^2}{k_{\bot}^2 \rho_e^2} - \frac{k_{\|}^2 \rho_e^2}{\beta_e}\right\} - \frac{k_{\|}^2 \rho_e^2 \tilde{\omega}_{e\|}^2}{{\rm \pi} k_{\bot}^6 \rho_e^6 } = 0 , \quad \end{equation}
where we have once again evaluated ![]() $F_i$,
$F_i$, ![]() $G_i$,
$G_i$, ![]() $H_i$,
$H_i$, ![]() $L_i$ and
$L_i$ and ![]() $N_i$ using (G35),
$N_i$ using (G35), ![]() $F_e$,
$F_e$, ![]() $G_e$,
$G_e$, ![]() $H_e$,
$H_e$, ![]() $L_e$ and
$L_e$ and ![]() $N_e$ using (G38),
$N_e$ using (G38), ![]() $W_i$,
$W_i$, ![]() $X_i$ and
$X_i$ and ![]() ${Y}_i$ using (G99) and
${Y}_i$ using (G99) and ![]() $W_e$,
$W_e$, ![]() $X_e$ and
$X_e$ and ![]() ${Y}_e$ using (G102), and neglected all terms that are small under the ordering (K61a,b). Solving for the non-trivial root of (K62) gives the expression (4.105) for the complex frequency of whisper waves.
${Y}_e$ using (G102), and neglected all terms that are small under the ordering (K61a,b). Solving for the non-trivial root of (K62) gives the expression (4.105) for the complex frequency of whisper waves.
K.3.13. Derivation of frequency and growth rate of the CES ordinary-mode instability
Because the low-frequency assumption ![]() $\tilde {\omega }_{e\|} \ll 1$ is broken in the regime of relevance to the CES ordinary-mode instability, the dispersion relation (K23) is not valid; to characterise these modes, we must instead return to considering the full hot-plasma dispersion relation.
$\tilde {\omega }_{e\|} \ll 1$ is broken in the regime of relevance to the CES ordinary-mode instability, the dispersion relation (K23) is not valid; to characterise these modes, we must instead return to considering the full hot-plasma dispersion relation.
We choose to categorise the ordinary-mode instability for modes with ![]() $k_{\|} = 0$. In this special case, the plasma dielectric tensor simplifies considerably, and has the convenient property that
$k_{\|} = 0$. In this special case, the plasma dielectric tensor simplifies considerably, and has the convenient property that
if the particle distribution functions have even parity with respect to the parallel velocity ![]() $v_{\|}$ (Davidson Reference Davidson1983) – a condition satisfied by the CE distribution functions (4.1). Thus, perturbations whose associated eigenmode satisfies
$v_{\|}$ (Davidson Reference Davidson1983) – a condition satisfied by the CE distribution functions (4.1). Thus, perturbations whose associated eigenmode satisfies ![]() $\widehat {\delta \boldsymbol {E}} = \widehat {\delta E}_z \hat {\boldsymbol {z}}$ decouple from other modes in the plasma. The dispersion relation for such modes follows from (2.4.1):
$\widehat {\delta \boldsymbol {E}} = \widehat {\delta E}_z \hat {\boldsymbol {z}}$ decouple from other modes in the plasma. The dispersion relation for such modes follows from (2.4.1):
In terms of matrices ![]() $\boldsymbol{\mathsf{M}}_{s}$ and
$\boldsymbol{\mathsf{M}}_{s}$ and ![]() $\boldsymbol{\mathsf{P}}_{s}$ defined by (2.97), this can be written
$\boldsymbol{\mathsf{P}}_{s}$ defined by (2.97), this can be written
For ![]() $k_{\|} = 0$, the matrix components
$k_{\|} = 0$, the matrix components ![]() $(\boldsymbol{\mathsf{M}}_{s})_{zz}$ and
$(\boldsymbol{\mathsf{M}}_{s})_{zz}$ and ![]() $(\boldsymbol{\mathsf{P}}_{s})_{zz}$ are given by (see (G17i) and (G93i))
$(\boldsymbol{\mathsf{P}}_{s})_{zz}$ are given by (see (G17i) and (G93i))
 $$\begin{align} (\boldsymbol{\mathsf{M}}_{s})_{zz} &={-} \sum_{n ={-}\infty}^{\infty} \frac{\omega}{\omega-n \tilde{\varOmega}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right), \end{align}$$
$$\begin{align} (\boldsymbol{\mathsf{M}}_{s})_{zz} &={-} \sum_{n ={-}\infty}^{\infty} \frac{\omega}{\omega-n \tilde{\varOmega}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right), \end{align}$$ $$\begin{align}(\boldsymbol{\mathsf{P}}_{s})_{zz} &={-} \frac{3 \epsilon_s}{2} \sum_{n ={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) ={-}\varDelta_s . \end{align}$$
$$\begin{align}(\boldsymbol{\mathsf{P}}_{s})_{zz} &={-} \frac{3 \epsilon_s}{2} \sum_{n ={-}\infty}^{\infty} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) ={-}\varDelta_s . \end{align}$$Therefore, the dispersion relation (K65) becomes
 \begin{align} k_{\bot}^2 d_e^2 & ={-}\sum_s \frac{m_e}{m_s} \left[\varDelta_s + \sum_{n ={-}\infty}^{\infty} \frac{\omega}{\omega-n \tilde{\varOmega}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\sum_s \frac{m_e}{m_s} \left[\varDelta_s + \sum_{n = 1}^{\infty} \frac{2 \omega^2}{\omega^2-n^2 \tilde{\varOmega}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]\, . \end{align}
\begin{align} k_{\bot}^2 d_e^2 & ={-}\sum_s \frac{m_e}{m_s} \left[\varDelta_s + \sum_{n ={-}\infty}^{\infty} \frac{\omega}{\omega-n \tilde{\varOmega}_s} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ & ={-}\sum_s \frac{m_e}{m_s} \left[\varDelta_s + \sum_{n = 1}^{\infty} \frac{2 \omega^2}{\omega^2-n^2 \tilde{\varOmega}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right]\, . \end{align}
Since the left-hand side of (K67) is real, and the imaginary part of the right-hand side is non-zero if and only if the complex frequency ![]() $\omega$ has non-zero real and imaginary parts, we conclude that all solutions must be either purely propagating, or purely growing modes. Looking for purely growing roots, we substitute
$\omega$ has non-zero real and imaginary parts, we conclude that all solutions must be either purely propagating, or purely growing modes. Looking for purely growing roots, we substitute ![]() $\omega = \mathrm {i} \gamma$ into (K67), and deduce that
$\omega = \mathrm {i} \gamma$ into (K67), and deduce that
 \begin{align} &\sum_s \frac{m_e}{m_s} \left[\sum_{n = 1}^{\infty} \frac{2 \gamma^2}{\gamma^2+n^2 \tilde{\varOmega}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ &\quad ={-} k_{\bot}^2 d_e^2 - \sum_s \frac{m_e}{m_s} \left[ \varDelta_s + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] . \end{align}
\begin{align} &\sum_s \frac{m_e}{m_s} \left[\sum_{n = 1}^{\infty} \frac{2 \gamma^2}{\gamma^2+n^2 \tilde{\varOmega}_s^2} \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_n\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] \nonumber\\ &\quad ={-} k_{\bot}^2 d_e^2 - \sum_s \frac{m_e}{m_s} \left[ \varDelta_s + \exp \left(-\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) {I}_0\!\left(\frac{k_{\bot}^2 \tilde{\rho}_s^2}{2}\right) \right] . \end{align}
Neglecting the ion contributions (which are smaller than the electron ones by a ![]() $(m_e/m_i)^{1/2}$ factor) and considering
$(m_e/m_i)^{1/2}$ factor) and considering ![]() $\varDelta _e < 0$, we arrive at (4.113).
$\varDelta _e < 0$, we arrive at (4.113).