List of symbols
d Grain diameter.
I Infiltration into the saturated layer.
k Intrinsic permeability.
k 11 Permeability parallel to the slope.
K 22 Permeability perpendicular to the slope.
k s Permeability of saturated layer.
l Inter-channel spacing.
L Length of flow through the saturated layer.
L Latent heat of fusion.
p c Capillary pressure.
q Flux in the saturated layer.
r Radius of largest circle which fits in a vein.
r p Radius of particle.
S w Liquid-water saturation, fraction of pore volume.
S wi Irreducible water saturation.
S * Effective water saturation, (S w-S wi)/(1-S wi).
t Time.
th Travel time for flow along layers.
t1 Travel time for flow perpendicular to layers.
T Temperature, °C.
T 0 Temperature of ice point, K.
u Volume flux of water, volume per unit area per unit time.
ω Width of a drain channel.
![]() Speed of propagation of value of u.
Speed of propagation of value of u.
α 5.47 × 106 m-1 s-I.
θ Ground slope.
dζ/dt Rate of propagation of wetting front.
ρ i Density of ice.
ρ s Dry density of snow.
ρ w Density of water.
σsg Solid-gas interfacial energy.
ϕ Porosity.
ϕc Effective porosity, ϕ(1–S wi).
Introduction
One of society's most significant interactions with snow and ice involves water run-off from melting glaciers and seasonal snow covers. There are many uses of water derived from snow and ice sources, including the generation of electricity, regeneration of soil moisture for agriculture and water supplies for communities. Often the water available to satisfy the competing users is not sufficient and a complicated system to apportion water among the users is necessary. Excessive water run-off also causes major problems when run-off from snow melt or glacial outbursts results in serious floods. Whether the immediate problem is too little or too much run-off, significant improvements can be made in our abilities to forecast, control, and use the world's snow and ice water resources.
One of the major features of water run-off from snow covers and glaciers is that the run-off is delayed. One example of the benefits of a snow cover occurs when snow falling on agricultural lands provides an insulating blanket which prevents excessive soil freezing and seed damage during the cold winter months. When air temperatures increase and snow-pack melting occurs, the soil can absorb much of the melt water for use during the growing season. Reference Dunne and BlackDunne and Black (1971) have shown that, even in hilly terrain, one-half of the melt water can move along sub-surface paths thus providing opportunity for recharging the ground-water and soil horizons.
The temporary storage of water in the form of a snow cover will be an increasingly important factor in the future. For example, the development of coal deposits in the Rocky Mountains states of the United States would require enormous quantities of water for the revegetation of land stripped of coal. The existing priorities for the use of snow-melt run-off will have to be restructured in order to facilitate development of the coal deposits without causing severe environmental damage. Of course, increasing the snowfall by weather modification is being considered (Reference WeisbeckerWeisbecker, 1974) .
Snow-cover run-off
Detailed studies of the surface-energy balance of a melting snow-pack were conducted in the 1950's and 1960's and resulted in a basic physical understanding of the snow-melt processes (e.g. Reference AndersonAnderson, 1968). The physical and mathematical description of snow melt on an hourly basis allows an accurate calculation of snow melt (Reference AndersonAnderson, 1976), which serves as the surface boundary condition for the calculation of water run-off. Although we have limited control over the timing of the snow melt, the most efficient utilization of the run-off depends upon our forecasting ability.
The development of methods for quickly and accurately assessing the water content of the areal snow cover at anyone time is a major problem and is receiving much attention from the remote-sensing community (e.g. Reference RangoRango, 1975). Other information which can best be obtained on the large scale includes the material properties of snow which are needed for hydrological forecasting. Snow depths and profiles of density, grain-size, and liquid-water content are the most important physical parameters of snow as a source of water and should be included in any hydrological forecasting scheme.
Hydrological practices
Hydrological forecasting has been characterized by the use of historical records as a basis for forecasting run-off. Theorization in the general field of hydrology intensified about 1950 (Reference ChowChow, 1964, p. 1-10) and has produced a tremendous amount of knowledge about the physical aspects of infiltration, ground-water, overland and open-channel flows. Snow and ice hydrology is still in its early stages of theorization and many benefits are yet to be realized. The study of water movement through snow is one example of recent advances made in snow hydrology, advances which are now being used to improve water run-off forecasting schemes. Reference AndersonAnderson's (1973) snow-melt run-off model uses the most advanced characterization of water flow through snow of any of the computerized forecasting schemes in operation. This characterization consists of attenuation, lag-time, and Iiquid-water-content relationships which were obtained from data on a mature* mountain snow-pack. No generalization of these relationships can be made to account for grain-size, layering, density, depth, antecedent moisture, etc., and yet these relationships work well for snow-packs similar to the one from which the data were taken. It is important to understand why and under what circumstances these relationships can result in accurate forecasts.
The rapid changes which occur following the introduction of liquid into a snow-pack a re called “melt metamorphism”. Prediction of water flow through snow during the period of melt metamorphism can only be accomplished through an understanding of the feed-back relationships between the flux of liquid water and the physical properties which control that flux. These feed-back relationships occur in both seasonal snow cover and glaciers, making their study among the most interesting in hydrology.
In snow, three processes occur which contribute to the “aging” of a snow cover. First, upon the introduction of liquid water, rapid grain growth occurs (Reference WakahamaWakahama, 1968) until grain diameters of about I mm are reached. During this period of rapid grain growth, the intrinsic permeability to flow can increase significantly because, as Reference ShimizuShimizu (1970) has shown, the intrinsic permeability increases as the square of the average grain diameter. Secondly, snow covers are generally stratified with distinct horizons separated by wind crusts or “ ice layers”. These thin dividers are fine-grained and considerably less permeable than the majority of the snow cover, hence they act as barriers to the downward percolation of the melt water, re-routing the flow in the down-slope direction (see Fig. 1). When liquid water moves into the snow-pack in large quantities, the permeability of the high-density layers increases rapidly (Reference GerdelGerdel, 1954). Thirdly, now generally densifies during melt metamorphism and, since permeability decreases rapidly with increasing density, the effect of density reduces the effects of grain growth and ice-layer decomposition.

Fig. 1. An idealized diagram showing the flow paths through a highly stratified snow-pack. The water moves laterally along ice layers and vertically through flow channels
Clearly the response of a snow cover to surface melting or rain-on-snow depends upon its history of exposure to liquid water. The maturing processes are highly variable from year to * In this context, a mature snow-pack is one which has experienced the grain growth, density increase and ice-layer decomposition which occurs upon the introduction of liquid water into the snow-pack. 574 year and location to location, a fact which complicates the application of a general flow theory to forecasting water run-off. In order to understand the relationship between the flow of water and the physical properties which are determined partly by the history of water movement, it is necessary to understand the basic characteristics of water flow through snow as a porous medium as well as the thermodynamics of the three phases of water in snow.
Flow in homogeneous snow
In spite of the layered nature of most snow covers, the most basic principles of water flow through snow can be best understood in terms of the principles governing flow through a homogeneous non-uniform matrix (see Reference Greenkorn and KesslerGreenkorn and Kessler (1969) for definitions of homogeneity, isotropy and uniformity). Basically, flow through a relatively homogeneous mature snow cover is similar to flow through any unsaturated large-grained medium. The study of flow through porous media is a highly developed speciality (e.g. Reference BearBear, 1972) in which snow can be considered as a particular case.
Snow has certain unique problems, such as rapidly changing density and grain-size upon the introduction of the liquid phase, but it also has some special advantages. Because of the rapid disappearance of the smaller grains and the highly unsaturated condition throughout most of a mature snow-pack, the role of pressure gradients is generally small and can be ignored (Reference WankiewiczWankiewicz, unpublished). With this simplification, the Darcian equation for the volume flux of water in the unsaturated portion of a snow-pack can be expressed as (Reference Colbeck and DavidsonColbeck and Davidson, 1973):
where α is a constant, k is the intrinsic permeability and S* is the effective water saturation. The effective water saturation is highly variable depending on both the magnitude of the surface flux and the permeability of the snow.
Reference ShimizuShimizu (1970) showed that
where both the grain size (d) and snow density (ρs) can change significantly during the lifetime of a snow cover.
For given conditions of the snow-pack, Equation (1) shows that the flux of water (volume per unit area per unit time) is uniquely related to the volume of water available to flow (S*). This flux-concentration relationship is combined with a continuity equation, a surface condition, and an initial condition to provide a description of the movement of water in time and 575 space. The nature of the flow is best described by the speed- flux equation (Reference ColbeckColbeck and Davidson, 1973)
This equation shows that the rate of movement of a value of flux is linearly related to ![]() whose magnitude can be determined from the grain-size and density of the homogeneous snow. Because of the cubic relation between flux and concentration as expressed by Equation (1), the speed of a value of flux (dz/dt|u) is linearly related to u ⅔ as expressed by Equation (3), therefore larger values of flux move much more rapidly through the snow than smaller values of flux.
whose magnitude can be determined from the grain-size and density of the homogeneous snow. Because of the cubic relation between flux and concentration as expressed by Equation (1), the speed of a value of flux (dz/dt|u) is linearly related to u ⅔ as expressed by Equation (3), therefore larger values of flux move much more rapidly through the snow than smaller values of flux.
The mode of flow of a wave of flux moving down through a snow-pack is an interesting example of wave movement controlled by a non-linear flux-concentration relationship. In Figure 2, an example of a calculated wave of melt water propagating downward in snow shows the important features of water movement. The wave of surface melt in this example is symmetrical but, as the melt water moves into the snow, the leading edge of the wave steepens and the trailing edge lengthens. At depth the flow of water is continuous because of the extended recession. The decreased peak, increased base flow, and skewed shape for flow at 4.3 m depth in are packed column of homogeneous snow are shown in Figure 3.

Fig. 2. A symmetrical wave of melt water introduced at the surface moves down through the snow. Its leading edge steepens as its trailing edge lengthens with depth (after Reference ColbeckColbeck, 1972).

Fig. 3. The computed and observed flows at 4.3 m. depth in homogeneous snow. The reduced peak flow, increased base flow and skewed shape arisefrom the non-linear flux-concentration relationship (after Reference ColbeckColheck and Davidson, 1973).
The success of the flow theory in repacked homogeneous snow shows that the basic physical ideas of multi-phase flow in porous media can be successfully applied to relatively homogeneous snow. However, the application of this theory to all natural snow covers cannot be assumed because many snow covers are highly anisotropic and heterogeneous. Accordingly, careful review of the properties of the layers, study of flow through layered media, and many field studies are necessary. The application of the homogeneous flow theory to three natural snow-packs is considered here:
(1) Reference SharpSharp ([1952]) observed the vertical descent of water through the firn of a glacier by collecting water in small interceptors at various locations. Sharp's results show melt-water wave features which are very similar to those observed in homogeneous snow and the analysis of his data shows that the homogeneous flow theory is useful at least in this deep glacial snow cover (Reference ColbeckColbeck, 1972). The validity of this test was limited by the fact that the water flowing at each depth was collected from such a small area. For purposes of hydrological forecasting, local variations in the flow field are ignored and averages over a large area are used. As a minimum, the flow field should be averaged on a scale equal to the thickness of the snow cover when water collection measurements are compared with theoretical predictions.
(2) Price (unpublished) successfully calculated both the surface-melt and the water movement rates on large study plots in the Canadian sub-Arctic. While the snow cover was atypical because of the relative absence of stratigraphic features, Price's results provided a general verification of the two-dimensional homogeneous flow theory. The question of the applicability of the theory in temperate regions was not resolved since most snow covers are highly stratified compared to the snow cover at this sub-Arctic site.
(3) At the Central Sierra Snow Laboratory in California, where the snow-pack is highly stratified, a large lysimeter (U.S. Army. Corps of Engineers, 1955) was used to collect melt water from an area of 55.7 m2• The surface flux* and measured run-off are shown in Figure 4 for 17 April 1954 when the snow depth was 1.57 m and the snow had been wet long enough to achieve a stable grain-size and density. The most straightforward way of judging the applicability of the homogeneous flow theory to the Sierra snow is by combining Equation (3) with the surface flow and run-off data for several days. The data points shown in Figure 5 are calculated from Equation (3) * The surface flux was calcula ted by Dr Eric Anderson of the National Weather Service from data reported by the V.S. Army. Corps of Engineers (1955) where dz/dt|u is simply the snow depth divided by the travel time for each value of u on the receding portions of the hydrographs. The fact that these data points can be represented by a straight line of slope k½ shows that Equation (3) can be used to calculate the recession portion of the hydrograph with a high degree of accuracy. The value of k½ϕe-1, the parameter which characterizes the snow-pack itself, is determined from Figure 5 and is used to construct an entire run-off hydrograph shown in Figure 4. The calculated and measured hydrographs compare favorably for that portion of the hydrograph following the measured peak but the calculated leading edge of the melt-water wave is not such a good representation of the observed wave-front.

Fig. 4. The calculated suiface melt, calculated run-off, and measured run-oil from the Central Sierra Snow Laboratory lysimeter on 17 April 1954. Snow depth was 1.57 m.
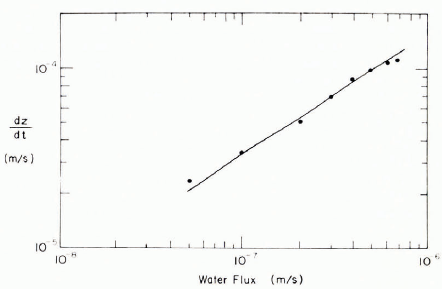
Fig. 5. The data points are calculated values of dz/dt|u for chosen values of u using the surface melt and measured run-off given in Figure 4. The straight line has a slope of ⅔ and represents Equation (3).
The theory described here involves very few mathematical difficulties because the pressure gradients were neglected during the formulation of Equation (I). The most important role of pressure gradients in unsaturated flow is to eliminate the shock front from the leading edge of the propagating wave by rounding the sharp corners and reducing the slope of the wave front. Thus by including the pressure gradients in the theory, the “goodness of fit” between the calculated and measured wave-fronts could be improved somewhat. However, as shown by more complete calculations of the wave-front (Reference ColbeckColbeck, 1974[a]), the inclusion of pressure gradients does not make a significant improvement.
Apparently the major cause for the dispersion of the wave-front is the stratified nature of the Sierra snow itself. This conclusion is reinforced by comparing the fronts of the melt-water waves in homogeneous (repacked) and natural snow-packs shown in Figures 3 and 4, respectively. Even at a depth of 4.3 m in repacked homogeneous snow, the wave-front rises rapidly to a peak, whereas, at a much shallower depth of 1.57 m in the Sierra snow, the front is dispersed in the same manner as the fronts observed in the glacial snow of upper Seward Glacier (Reference SharpSharp, [1952]). The apparent explanation for the early arrival of water to start the build-up of the wave-front is by-passing of water by the large-grained flow channels described by Reference GerdelGerdel (1954). No physical description has been made of the simultaneous flows through and between these channels partly because of the lack of quantitative information about their geometry and permeability, an important gap in our knowledge of snow covers.
Because the shock-front solution is not a good representation of the melt-water wave front in the Sierra snow cover, the peak flow is overestimated and consequently the lag time to the peak flow is underestimated. This weakness of the homogeneous flow theory is partly overcome by the fact that the procedure for routing the water through the saturated layer at the base of the snow cover averages the input from the unsaturated layer. Accordingly, the steep wave front of the calculated flow into the saturated layer will be smoothed and some of the difference between the calculated and measured flows in Figure 4 will disappear once the melt water is routed along the base of the snow cover.
In addition to the high degree of dispersion of the wave-front in most natural snow covers, the major problem with the use of the homogeneous flow theory is the evaluation of the parameter k½ϕe-1 This parameter can sometimes be calculated from knowledge of the snow density and grain-size, a procedure which worked well for the relatively homogeneous isotropic snow-pack studied by Price (unpublished). For the stratified snow covers typical of the more temperate regions, an equivalent value of k½ϕe-1 can be calculated from surface-melt and run-off data. During the early stages of snow melt, when rapid changes are taking place in the properties of the snow, this parameter must be updated frequently as the snow matures. However, the best procedure for doing this is not apparent at this time because of the lack of investigations of snow-melt run-off during the period of melt metamorphism.
Given the complexity of the processes acting on the snow cover during the period of melt metamorphism, perhaps it is too much to expect that a single parameter, k½ϕe-1, can represent the properties of the snow cover. For example, two independent values of permeability are required to describe flow through a sloping layered snow cover (Reference ColbeckColbeck, 1975); the permeabilities perpendicular and parallel to the slope must each be known to calculate k½ϕe-1 from measurements of the snow properties. The ideal method of determining this critical parameter would be to calculate it directly from large-scale measurements of grain-size, density, ice-layer extent, ete. In the next section some of the basic principles controlling these properties are described in the hope that they can be incorporated into a physical model of snow-melt run-off. Later, the validity of the concept of an “equivalent snow-pack”, i.e. choosing a single value of k½ϕe-1 to represent a highly stratified heterogeneous snow cover, is discussed.
Time-dependent and heterogeneous features if snow
The temperature at which the three phases of water in highly unsaturated snow are m equilibrium is given by (Reference ColbeckColbeck, 1973)
where the capillary pressure (pc) increases as the liquid saturation decreases and r p is the mean geometrical radius of the ice particles. For a given liquid saturation and capillary pressure, the temperature differences among particles of different radii cause heat flow to the smaller particles which disappear by melting. The rate at which the smaller particles disappear and the larger particles grow is determined in part by the degree of liquid saturation. At lower saturations the grain-effect on temperature is dominated by the capillary pressure effect and, with less area of liquid available for heat flow between the particles, the rate of grain growth decreases. In order successfully to model the grain-growth process in a snow cover, the history of liquid saturation of the snow cover will have to be considered.
The history of liquid saturation is also important regarding the degeneration of ice layers and the development of large-grained drainage channels. Upon the introduction of large quantities of liquid water in the snow cover, the small intercrystalline veins in ice layers melt out because their phase-equilibrium temperature decreases with size. Neglecting any gaseous phase, Equation (4) can be simplified to (Reference LanghamLangham, 1974)
where r is the largest circle which can fit inside the vein. As the veins increase in size, their permeability increases rapidly and water is capable of moving directly through them.
Clearly, a combination of flows occurs simultaneously during water movement through snow including flow down drainage channels, flow along and through ice layers, and flow through the relatively homogeneous snow of each layer. The homogeneous snow generally constitutes the bulk of the snow cover and yet the other features can dominate the flow. For example, the travel time for a value of flux in a layered snow cover is greater than the travel time as determined for homogeneous snow from Equation (3). The ratio of travel times for homogeneous (t h) and layered (t l) snows is (Reference ColbeckColbeck, 1975)
where k 11 is the permeability of the more or less homogeneous snow parallel to the slope and k 22 is the effective permeability perpendicular to the slope. In the presence of wind crusts or ice layers, kII is larger than k 22 and the run-off is delayed accordingly. Once the ice layers develop a high permeability in the presence of liquid water, k 22 is increased and the difference between t h and t l is reduced accordingly. The period when these changes occur should be a subject of intense study.
Time delays in water run-off
During the ripening and maturing of a snow cover, various mechanisms operate to delay water run-off. These mechanisms range in scale from the hourly delay associated with the propagation of melt-water waves to the longer seasonal delay of the snow-deposition- run-off cycle. One important mechanism is the propagation of a “wetting front” into dry snow. The most intense wetting fronts arise from heavy rains falling on a sub-freezing snow. Part of the infiltrating water freezes and releases the latent heat needed to raise the snow temperature to the melting temperature. Additional liquid is retained by capillary action, especially in fine-grained wind crusts. As the snow grains become rounded and grow during melt metamorphism, some of this capillary water is released and adds to the base flow. Another important mechanism, the impounding of flow by ice layers, delays the run-off by hours. In effect, the ice layers add a diffusion factor to the diurnal flow, whereas the temperature and capillary effects cause temporary storage lasting from days to months.
The forecasting of liquid infiltration into a dry snow cover is an important aspect of hydrological forecasting because of the wide variety of responses which can occur. Rain on dry snow produces everything from no run-off to serious flooding depending on many important factors. The liquid moves downward as a distinct “wetting front” (Reference YosidaYosida, 1973) at a speed given by (Reference ColbeckColbeck, 1976[a])
where u and S w are the water flux and saturation just above the wetting front. Often the first term in the denominator dominates the second term because most of the water supplied to the front is used to raise the saturation to the level necessary to satisfy the flux-concentration relation, whereas the thermal requirement is relatively small. This simplifies the use of Equation (7) so that the analysis of the movement of a uniform wetting front becomes straight-forward.
Even assuming a completely uniform frontal movement, it is easy to understand why rain on snow produces a wide variety of responses. The grain-size and intensity of rain are the most important parameters determining propagation through a homogeneous isotropic snow cover; however, the assumption of a uniform snow cover is generally unrealistic. Even for the relatively deep and homogeneous mountain snows, wetting-front advance follows distinct routes and leaves cold dry areas of snow behind (see fig. 1 or pl. 8-1 of U.S. Army. Corps of Engineers, 1956). This concentration of flow accelerates the movement of the wetting front by a factor of (1 + l/w) ½ where w is the width of a drain channel and l is the inter-channel spacing. Statistically significant samplings of channel geometries have not been made but they must vary significantly depending on the location, year and history of the snow cover.
For forecasting purposes, it may be adequate to assume values for wand l but, until detailed observations are made of the channel geometries, much uncertainty would be associated with the assumed values. Reference Hill and ParlangeHill and Parlange (1972) provided some insight into the formation of flow channels in stratified soils but this type of investigation has yet to be done for snow. Once the flow channels are established, their permeability increases rapidly because of grain growth and frictional melting, hence, they become preferential routes for subsequent flow. As the entire pack slowly imbibes liquid water and eliminates the isolated pockets of sub-freezing snow, ice-layer decomposition and grain growth tend to smooth the material properties such that deep snow-packs exhibit a fairly uniform flow field after their melt metamorphism is complete. As shown earlier for the case of the Sierra snow cover, once mature, a deep snow-pack responds very quickly to surface inputs and can be characterized as homogeneous with at least some accuracy. The most discouraging aspect of applying this information to snow-melt flood forecasting is simply the fact that shallow prairie snow covers are often the sources of the worst floods. Shallow snow cover s can disappear by melting long before melt metamorphism can homogenize the snow, and therefore cannot be so readily classified as homogeneous. Unlike deep mountain snow covers, shallow snow covers commonly experience diurnal freeze- thaw cycles throughout their entire depth, a fact which further complicates the application of predictive models (Reference Male and GrayMale and Gray, 1975)
Basal flow and water exchange with the ground
As in flow through the unsaturated layers, flow along the base of the snow cover has been treated in an idealistic way. Overland flow in the absence of a snow cover is normally described as sheet flow (Reference EaglesonEagleson, 1970, p. 325), where the flow concentrates into increasingly large streams. In the case of snow-covered terrain, these streams cause sub-surface melting due to frictional heating such that open channels develop and enlarge throughout the melt season. As the channels enlarge, they decrease the response time of the snow cover because flow through saturated snow is slower than flow in open channels. In spite of their obvious importance, there is almost a complete lack of information about the spread of the channels beneath the snow cover.
The mode of flow of the sheet of water moving through snow over ice or soil is significantly different than that of the upper unsaturated layers. This basal flow essentially integrates and smooths the waves of water arriving from the surface. The degree of smoothing depends upon the ground slope (θ) and length of run to an open stream (L). The lateral flux is given by (Reference ColbeckColbeck, 1974[b))

where the time period of integration, t L–t 0, is given by
where ϕ and k s are the porosity and permeability of the saturated layer.
Another important topic, the interaction between the soil and snow cover, has been widely recognized (Reference Dunne and BlackDunne and Black, 1971; Reference PeckPeck, 1974), but it is very difficult to include in forecasting schemes because of the variety of conditions which occur in different areas and in different years. The permeability of the upper soil layers depends on the soil type and temperatures which prevail throughout the period of snow cover. Northern areas are characterized by soil-water depletion because of the upward migration of water vapor (Reference Trabant and BensonTrabant and Benson, 1972), whereas some areas experience a net gain of soil water while snow-covered. Sometimes, heavy ice layers form at the soil surface, blocking infiltration and encouraging rapid run-off and snow-melt floods. During other years the soil absorbs most of the snow melt and smaller volumes of run-off occur. Little attempt has been made to combine the snow and ground-water regimes, although studies of the two as separate systems have been fairly successful. The need for combining these two elements of the hydrosphere is immediate.
Limitations of physical models in hydrological forecasting
Many of the problems with perfecting a physical model of snow run-off have been mentioned. We may not even have adequate techniques for identifying the areal extent, thickness and permeability of ice layers nor the size and distribution of under-snow channels. Until proven techniques are available, it may not be possible to follow the development of these or other features throughout the melt season and it may be very difficult to assign the critical values of k½ϕe-1 and L to a snow cover for forecasting purposes.
As described earlier, deep snow covers in temperate climates are often moist throughout the winter and are highly mature by the time the melt season begins. Under these circumstances, many properties of the snow throughout most of the melt season are similar to those of a stable homogeneous snow cover and run-off forecasts can be made using models which include physical relationships. While physical models do offer some advantages over the empiricallag and attenuation methods like the “Muskingham method”, it must be mentioned that these empirical techniques work rather well in a situation where the snow is stable thermodynamically and historical records are available to serve as a guide. The main advantages of models which include some physical aspects would occur in situations where the properties of the snow are undergoing rapid changes or are significantly unusual. Then, as long as the properties of the snow cover can be adequately represented, the effect of some particular parameter could be factored into the model to account for any deviation from the usual behavior.
In its simplest form, a physical model would treat a snow cover as “equivalent porous medium” which would be characterized by a single value of k½ϕe-1 While most ground-water or petroleum reservoir calculations are based on the concept of an equivalent medium, Reference FreezeFreeze (1975) has recently shown that, at least for ground-water, the validity of this concept is questionable. Accordingly, it must be determined when a snow cover can be represented by a model which does not account for the three-dimensional and temporal variations in its material properties. A meaningful test of the concept of an equivalent porous medium is difficult because of the lack of detailed knowledge about the structure and variability of snow covers. For example, the occurrence of ice layers and drainage channels appears to be partly stochastic and partly deterministic, but we have no knowledge of the frequency distribution in time and space of their size and permeability. For geological formations, the probability distribution function for permeability has been shown to be log normal, whereas that for porosity is normal (Reference FreezeFreeze, 1975). Much work needs to be done to establish these relationships for snow in both the fresh and mature states. Until the effect of the variability of the properties of a snow cover are established with a stochastic-conceptual model like Freeze's (1975), the use of any model for forecasting run-off from a snow cover undergoing rapid metamorphism would be risky.
One important step in developing a forecasting capability for a snow cover undergoing melt metamorphism is the construction of a multi-dimensional time-dependent model of a rapidly changing snow cover. Reference AndersonAnderson (1976) has begun this task with a one-dimensional model which accumulates and ablates the snow cover throughout the period of snowfall and 582 snow melt. To this model we must add the spatial variations which often control the flow field and, therefore, the timing of the snow-melt run-off.
Glacial run-off
Many important aspects of glacial run-off have already been covered because of the similarities between snow and glacial hydrology. First, glaciers are snow-covered most of the year so water flow through snow is an integral part of glacial hydrology. Secondly, many similarities exist between the problems of the flows through snow and ice. The majority of the flow through ice appears to be through conduits which enlarge by frictional heating and/or hydrostatic pressure differences and are analogous to the drainage channels and under-snow channels which sometimes dominate the flow through snow. The basal flow over glacial bedrock occurs both in sheets and open conduits whose geometry is not well understood. Furthermore, these conduits are highly variable in time because of the varying amount of water available for run-off and their tendency to contract as the water flow decreases. Of course, some time lag is associated with the adjustment of the conduits such that the timing of the seasonal run-off is complicated. To understand glacial run-off, we must understand the geometry and temporal variations of the system of glacial conduits. Only then can the question of the predictability of glacial run-off in all situations be resolved.
Glacial passages
Water enters glacial ice via many conduits ranging in size from intergranular veins to large crevasses. Hydrologically, the veins are only significant water passages close to the surface where they are enlarged by radiation absorption. Reference Wakahama and G.Wakahama and others (1973) found that the permeability of veins close to the surface of Mendenhall Glacier increased significantly during the summer months but it was still about two orders of magnitude less than snow. Reference Raymond and HarrisonRaymond and Harrison (1975) found that veins below 7 m depth in Blue Glacier were not large enough to be significant water passages. Raymond and Harrison observed the presence of air in the veins, an effect which requires the description of flow through veins as unsaturated flow through porous media (Reference ColbeckColbeck, 1976[b]). Regardless of how the flow is described, the veins are probably not capable of conducting away a large portion of the surface run-off, a suggestion which was made originally by Reference NyeNye and Frank (1973). Reference Raymond and HarrisonRaymond and Harrison (1975) observed small conduits in cores taken from Blue Glacier, and, in fact, conduits of various sizes are commonly observed in tunnels and crevasse walls of temperate glaciers. Reference ShreveShreve (1972) suggested that a tree-like system of passages penetrates the ice from surface to bed. In this scheme, smaller passages join to form larger passages until the bed is reached. This stream-like series of passages is analogous to surface stream systems and suggests that standard river-forecasting techniques might be applicable to forecasting glacial run-off. The glacial passages, however, are highly variable seasonally and may develop with distinct characteristics depending on the individual glacier.
Flow along the bed occurs primarily in channels cut in the ice (Röthlisberger, 1972), channels cut into the bed (Reference Nye and FrankNye, 1973) and/or in a thin sheet (Reference WeertmanWeertman, 1972). Water passages cut into the bedrock have not been generally observed (Reference Embleton and KingEmbleton and King (1968) as cited by Reference MeierMeier (1973)) in deglaciated areas so englacial tunnels and/or sheets appear to carry most of the water run-off.
A seasonal time lag for release of melt water from glaciers has been established (Reference StenborgStenborg, 1970; Reference TangbornTangborn and others, [1975]) and can probably be explained in two ways (see Fig. 6). First, early in the melt season a glacier is snow-covered and a large-liquid water deficit must be satisfied before the firn and water-holding capacity of the snow is filled. Even if the snow and firn are already “ripe”, a liquid deficit exists because of the need to satisfy the fluxconcentration relationship given as Equation (1). Following the introduction of large 583 quantities of water as the melt season progresses, the release of stored water from the snow cover on a glacier occurs for the reasons given in the preceding section. T he snow cover, however, is probably not the major factor in delaying the water run-off as illustrated in the extreme cases by jokulhlaups and outbursts of glacier-dammed lakes. Once the early-season melt water enters the existing network of intraglacial conduits and subglacial channels, these conduits enlarge by kinetic heating and/or excess hydrostatic pressure of the water column. Prior to the enlargement of the subglacial channels, it would seem possible for the sheet flow to make a major contribution to the base flow experienced throughout the winter months. As the channels grow, the larger ones appear to capture most of the flow because the pressure in the channels decreases with increasing discharge (Reference RöthlisbergerRöthlisberger, 1972). Once fully developed, melt-water channels can be direct passages from the surface to the terminus of a glacier. Dye-tracing studies have shown water speeds of 0.5 m s-1 through these conduits (Reference StenborgStenborg, 1969; Reference Behrens, H., H., H., W. and O.Behrens and others, 1975), although the speed of a tracer is greatly reduced if placed on a snow surface instead of directly into a conduct (Reference KrimmelKrimmel and others, 1973), During the later part of the ablation season, the rapid movement through conduits in the ablation zone of a glacier suggests that they are often direct channels to the terminus.

Fig. 6. The seasonal delay in melt-water run-off from a glacier is illustrated after Reference StenborgStenborg (1970).
Although not much is known about the details of the conduit system (Reference MeierMeier, 1973), it is clear that the conduits are highly variable in time and space. The situation may not be as complicated as the drainage channels which form yearly in the snow cover, because conduits in glaciers tend to form initially where crevasses present an opportunity for water entry (Reference StenborgStenborg, 1969). Once open, these conduits are not likely to close completely to the surface over the winter months and should be available for re-opening during the subsequent melt season.
Direct measurements of the highly variable glacial “water table” have been made by Reference HodgeHodge (1976) by drilling into the water table of a temperate glacier. Fluctuations of the water table of 40 m were noted over several days and phase shifts of about 2 d were observed between a peak surface flow and water-table response. On another temperate g lacier, Reference HodgeHodge (1974) found that the amount of liquid water in the glacier at any time correlated well with the 583 sliding speed of the glacier, suggesting that the hydrostatic pressure of the water at the bed dominated the mechanics of sliding. The sliding phenomenon must in some cases tend to close off the subglacial conduits (Reference Nye and FrankNye, 1973) and have an important effect on the hydrological response of the glacier to intense summer melting.
Temporal variations and predictability
Reference StenborgStenborg (1970) found that 25 % of the water run-off during the summer months was delayed from early summer until the middle of the summer. The apparent explanation for this is the delayed run-off from the firn and snow as well as the time delay to re-op en conduits in the ice and along the bed. Openings near the bed of a temperate glacier have been observed to close in a matter of days because of the high level of deviatoric stress and overburden pressure along the ice- rock boundary. Clearly, these passages are capable of closing after the melt season when only the receding flow from the snow and firn supplies water to the conduits. Modeling their opening and closing on a seasonal time-scale is one of the most significant problems in glacial hydrology. The most straightforward model would generate an equation comparable to Equation (7) and would describe the advancing front of conduit dilatation. Like the propagating wetting front in snow, glaciers delay water run-off while increasing their ability to transmit the water. Once the transitional stage of conduit dilation has been completed, run-off prediction using either physical or statistical models should be possible. As with the snow cover, forecasting may be inaccurate during the transient period of conduit enlargement.
These are three of the basic questions which must be answered before a satisfactory physical model of glacial run-off can be formulated:
(1) What percentage of the same melt-water conduits regenerate each summer?
(2) How does the formation of these conduits vary among different glaciers and in different years?
(3) How do these conduits connect with the perched water table at the firn-ice transition?
Hydrologically, a glacier can be represented as a series of reservoirs (Reference EllistonElliston, 1973; Reference Nilsson and SundbladNilsson and Sundblad, 1975) with diurnal impulses imposed on a base flow. Unfortunately, even for a given glacier, the reservoir constants are functions of time (Reference EllistonElliston, 1973) because the physical mechanisms, which account for the passage of water, are generally only stable during the latter par t of the ablation season. Reference Nilsson and SundbladNilsson and Sundblad (1975), for example, successfully used a three-reservoir model to describe a 17 d period during August in northern Sweden. However, Reference GolubevGolubev (1971) and Reference LangLang (1973) found significant decreases in the lag-to-peak run-off as the ablation sea son progresses, a result which is clearly consistent with present knowledge of the physics of water flow through both snow and glacier conduits.
In spite of the physical complications associated with calculating surface melt and routing melt water through snow covers and glaciers, forecasting schemes of some practical significance have been established for both daily (Reference DerikxDerikx, 1973; Reference ØstremØstrem, 1973) and seasonal (Reference Tangborn and RasmussenTangborn and Rasmussen, 1976) run-off from glacierized basins. Further refinements in our ability to forecast run-off are necessary because of the increased demands being placed on our water resources and because of our increased activities in areas affected by snow and ice run-off. For example, Reference BjörnssonBjörnsson (1974), in a detailed study of the periodic jökulhlaups from the Grimsvötn area of Vatnajökull, showed that the majority of the wa ter accumula tes because of excessive geothermal heat flux and that 20 m3 s-1 would have to be removed con tinuously to prevent the accumulation of water which leads to the rapid and destructive subglacial discharges. The glacier outburst floods reported by Reference RichardsonRichardson (1968), Reference Post and MayoPost and Mayo (1971) and Reference MathewsMathews (1973) show the significance of glacial outburst problems in other areas.
Conclusion
Rivers in any given area usually exhibit similar, time-invariant hydrological characteristics and the calibration of forecasting models made on one river can usually be applied to many rivers in that area. The snow cover in any area may exhibit significantly different hydrological characteristics from one week to another depending on the degrees of melt metamorphism or the permeability of the snow- soil horizon. Glaciers in anyone area may exhibit significantly different hydrological characteristics depending on their size, shape, geothermal heat input, etc. Thus, while ice-free river systems are mostly fixed in their hydrological response to given inputs, snow covers and glaciers are far more variable. The research necessary to develop adequate knowledge of snow covers and glaciers as hydrological systems is far from complete.
The best possible understanding of any hydrological system requires a combination of the physical and stochastic approaches (Reference YevyevichYevyevich, 1974). This combination offers many exciting challenges for glaciologists.
Acknowledgements
I thank Daryl Calkins, Michael Bilello and Nancy Parssinen for reading the manuscript and offering suggestions for its improvement. The generous support of projects 4AI61102AT24/A1/001 and 1F161102B52A/02/009 have made possible my work on wet snow at CRREL.
The encouragement and support of Drs G. D. Ashton and K. F. Sterrett is also gratefully acknowledged. Dr Eric Anderson of the National Weather Service generously provided the calculated values of surface flux shown in Figure 4 as well as comments on the manuscript.
Discussion
E. M. Morris: Under what temperature conditions did you perform your laboratory experiments on percolation of water through snow? When water flows through snow there is the possibility of change of phase (i. e. proportions of fluid and matrix) which is not a feature of flow through most porous media.
S. C. Colbeck: Our experiments on the flow of water through columns of homogeneous snow were done with the columns buried in the firn of a temperate glacier. Therefore, only the tops of the columns were exposed to temperatures other than 0°C. We have modelled the advancing “wetting front” of liquid water penetrating a sub-freezing snow cover as well as the effect of radiation penetration of causing sub-surface melting. The “wetting front” is of much practical interest, but the effect of radiation penetration can be neglected for all practical purposes.
J. Martinec: If we speak about run-off forecasts, it is necessary to deal not only with melt water leaving the snow-pack but also with that reaching a stream channel or the outlet of a basin. In your illustration (Fig. I), indicating overland flow, there should be an additional component for melt water infiltrating into the soil. This may be more important in some areas than the surface flow. The same remark applies to glaciers where flow should, in some cases, be considered as part of the ground-water system.
Colbeck: I certainly agree that the soil- snow interaction is very important. Dunne and Black, for example, have shown that 50% of the snow-melt run-off can move along subsurface paths depending upon the permeability of the soil. During some years this permeability may be very low and rapid run-off and flooding potentials exist. During other years much of the run-off enters the soil thus reducing the flooding hazard and providing opportunity for recharging the ground-water and soil horizons. At this time we need to combine the work accomplished on snow and ground-water hydrology.
G. J. Young: You have dealt primarily with seasonal and daily run-off. The role of climate is important in changing future run-off contributions from glacier-fed systems. Would you comment on the importance of long-term as opposed to short-term thinking?
Colbeck: I do not wish to add anything about climatic predictions to what Professor Dansgaard said in his Special Lecture. The problem of water release from glaciers is very complicated because it is possible 10 have the release of large quantities of melt water and the growth of glaciers simultaneously. This depends upon the exact nature of the climatic change and the interaction between particular glaciers and local climate. While this is a serious problem in areas which use glacial melt water, I cannot make any particular predictions about the availability of glacial run-off for the future.








