1. Introduction
Particle-laden flows of non-Newtonian fluids are widely encountered in the natural and industrial areas. Examples of these particle-laden non-Newtonian flows include fibre-reinforced polymers or rubbers (D'Avino & Maffettone Reference D'Avino and Maffettone2015), red blood cell (RBC) transport in the vessels (Ye, Phan-Thien & Lim Reference Ye, Phan-Thien and Lim2016; Beris et al. Reference Beris, Horner, Jariwala, Armstrong and Wagner2021), viscoelasticity-based cell separations in microfluidics (Lin & Huo Reference Lin and Huo2015; D'Avino, Greco & Maffettone Reference D'Avino, Greco and Maffettone2017; Li & Lin Reference Li and Lin2022), the fibre-like microorganisms swimming in non-Newtonian fluid environments (Storm et al. Reference Storm, Pastore, MacKintosh, Lubensky and Janmey2005; Li & Ardekani Reference Li and Ardekani2016), just to name a few. All these suspensions mentioned above can exhibit peculiar features, such as viscoelastic and shear-thinning effects. It is well known that these non-Newtonian characteristics can significantly influence the behaviour of particles in fluid flow. Needless to say, the particle dynamics will conversely affect the bulk properties of suspensions (Ngo, Nguyen & Oh Reference Ngo, Nguyen and Oh2021). Thus, from both the fundamental and the applied perspectives, understanding the dynamics of particles is important for designing and optimizing industrial applications involving non-Newtonian particulate two-phase flows. To uncover the statistical physics of the collective distribution and orientation of particles, it is, first of all, of importance to understand how a single particle orientates and rotates in non-Newtonian flows.
The particle dynamics in shear flows has been widely explored in previous studies. For a single particle rotation in an unconfined shear flow, Jeffery (Reference Jeffery1922) first derived the angular velocity of a non-spherical particle immersed in a simple shear flow of Newtonian fluid, ignoring both fluid and particle inertia. The results indicate that the particle rotates around the vorticity axis along different closed orbits (so-called Jeffery orbits) with different initial orientations. There exist abundant studies on the modulations of Jeffery orbits due to fluid or particle inertia (Taylor Reference Taylor1923; Saffman Reference Saffman1956; Lundell & Carlsson Reference Lundell and Carlsson2010). Rosén, Lundell & Aidun (Reference Rosén, Lundell and Aidun2014) and Rosén et al. (Reference Rosén, Do-Quang, Aidun and Lundell2015a) conducted a systematic study on the effect of fluid inertia on the rotation mode of a neutrally buoyant particle with different Reynolds numbers. Besides the fluid and particle inertia, the rheological characteristic of the fluid flow is another factor affecting the particle rotation modes. Considering that viscoelasticity is a typical rheological characteristic of non-Newtonian fluids, the rotation modes of a single particle in viscoelastic fluids have long been actively investigated.
The studies on particle rotational dynamics in viscoelastic fluid flows began with spherical particles. When the elastic effect of fluid is weak, the theoretical results show that the particle angular velocity is almost unchanged in the second-order fluid (SOF, a kind of weakly viscoelastic fluid) (D'Avino & Maffettone Reference D'Avino and Maffettone2015). However, when the particle is immersed in a fluid with strong viscoelasticity, both experimental and numerical results evidence that the fluid elasticity can dramatically slow down the particle rotation rate (Hwang, Hulsen & Meijer Reference Hwang, Hulsen and Meijer2004; D'Avino et al. Reference D'Avino, Hulsen, Snijkers, Vermant, Greco and Maffettone2008; Snijkers et al. Reference Snijkers, D'Avino, Maffettone, Greco, Hulsen and Vermant2009; Housiadas & Tanner Reference Housiadas and Tanner2011; Snijkers et al. Reference Snijkers, D'Avino, Maffettone, Greco, Hulsen and Vermant2011). Snijkers et al. (Reference Snijkers, D'Avino, Maffettone, Greco, Hulsen and Vermant2011) numerically explored the rotational dynamics of a spherical particle in the Oldroyd-B fluid, the results indicate that the closed orbits around the particle become distorted and form two recirculation regions, which are opposite to the primary flow.
Regarding non-spherical particles, researchers devoted efforts to investigating the rotational behaviours of ellipsoids in viscoelastic fluid flows by experiments. These experimental studies show that the viscoelasticity could significantly increase the particle rotational period (Gauthier, Goldsmith & Mason Reference Gauthier, Goldsmith and Mason1971). Apart from the particle rotation rates, the Jeffery orbits can also be affected by fluid rheology. Experiments, indeed, indicate that, when fluid elasticity is weak, the symmetry axis of rod-like particles eventually drifts to the vorticity direction, whereas it aligns in the shear plane for disk-like particles (Gauthier et al. Reference Gauthier, Goldsmith and Mason1971). However, moderate and strong fluid elasticities lead to distinct particle orientations, which have been demonstrated by experiments of red blood cell in a Boger fluid flow (Johnson, Salem & Fuller Reference Johnson, Salem and Fuller1990). In moderately elastic fluids, it was observed that the ellipsoidal cells orientate between the vorticity and flow directions. In highly elastic fluids, the fibre-like particles align their symmetry axes along the flow direction (Iso, Cohen & Koch Reference Iso, Cohen and Koch1996a; Iso, Koch & Cohen Reference Iso, Koch and Cohen1996b). Later, several more detailed experiments were conducted to analyse the effect of a wide range of fluid elasticities on the orientations of ellipsoids with different shapes (aspect ratio ranges from 2.0 to 8.0) (Gunes et al. Reference Gunes, Scirocco, Mewis and Vermant2008). Besides the aforementioned particle orientations in weakly and highly elastic fluids, there exists a more interesting particle orientation mode characterized by the bimodal distribution in a viscoelastic shear flow with a specific range of Deborah numbers (Gunes et al. Reference Gunes, Scirocco, Mewis and Vermant2008).
As for the theoretical studies, Leal (Reference Leal1975) derived an asymptotic solution for a rod-like particle immersed in the shear flow of a SOF fluid. The orientation modes predicted by the theoretical model are consistent with the experiments: rod-like particles evolve towards the vorticity axis in shear flows with low Deborah number, while they align along the flow direction in high Deborah number flow. Brunn (Reference Brunn1977) further extended the theoretical model to the ellipsoids with other aspect ratios. Moreover, Dabade, Marath & Subramanian (Reference Dabade, Marath and Subramanian2015) proposed a viscoelastic torque model based on the generalized reciprocal theorem. This model predicts the longside-on orientation for both prolate and oblate particles in the uniform flow of viscoelastic fluids, in which the first normal stress difference of fluid is positive and dominant.
Considering the limitation of the small expansion parameters used in the asymptotic theory, theoretical studies are mainly restricted to weakly viscoelastic fluids, such as a SOF. The results predicted by this theorem could not reveal the more complex orientation modes (such as the orientation between the vorticity and flow directions) observed in experiments. In addition, the theoretical approaches also could not be used to handle the more realistic fluids described by the highly nonlinear constitutive equations, such as the Giesekus model. Thus, to understand the mechanisms of the particle behaviours in fluid flows with more complex rheological properties, numerical approaches are needed. Numerical simulations of the rotational dynamics of ellipsoids in viscoelastic shear flows have received extensive attention (Phan-Thien & Fan Reference Phan-Thien and Fan2002; Nguyen-Hoang et al. Reference Nguyen-Hoang, Phan-Thien, Khoo, Fan and Dou2008; Wang, Yu & Lin Reference Wang, Yu and Lin2019). D'Avino et al. (Reference D'Avino, Hulsen, Greco and Maffettone2014) and D'Avino, Greco & Maffettone (Reference D'Avino, Greco and Maffettone2015) systemically analysed the detailed dynamics of prolate particles in a sheared Giesekus fluid by finite element simulations. Due to the fluid elasticity, the particle rotation could be categorized into four different modes: (i) in low Deborah number flow, the prolate particles align their symmetry axes along the vorticity direction and behave in a ‘log-rolling’ mode. (ii) With increasing shear rate or fluid elasticity, the particles drift towards the shear plane and finally align between the flow and vorticity directions. (iii) When the Deborah number reaches a critical threshold value, an interesting bi-stable orientation mode appears. In this rotation mode, the final equilibrium state of a particle depends upon its initial orientations. (iv) Finally, in highly elastic flow with large Deborah number, the particles eventually align with the flow direction.
To summarize, although there are a few studies on the rotational dynamics of non-spherical particles in viscoelastic flows, these studies are mostly confined to flows which are fluid elasticity dominated, where the fluid and particle inertia are both absent. The interplay between fluid elasticity and inertial effects on particle behaviours in shear flows is not yet explored. The elasto-inertial coupling effect is expected to affect the particle dynamics. For example, induced by the competition between fluid inertia and elasticity, the particles exhibit a different lateral migration in duct flows (Li, McKinley & Ardekani Reference Li, McKinley and Ardekani2015; Yu et al. Reference Yu, Wang, Lin and Hu2019). However, in viscoelastic flows with fluid inertia, the research on this coupling effect on particle rotational behaviours is still developing.
The main dimensionless numbers governing the particle dynamics in viscoelastic flows include the Reynolds number, Re, Stokes number, St and Weissenberg, Wi or Deborah number, De. The previous studies are mostly confined to inertia-free particles immersed in viscoelastic flows within the Stokesian regime, i.e. 
$Re, St \sim 0$ and Wi or 
$De > 0$. From this point of view, there exist gaps in the parameter space, where fluid inertia, particle inertia and fluid elasticity coexist in the suspension system (
$Re > 0, St>0$, Wi or 
$De > 0$). The present research aims at mapping the parameter space and understanding the influences of the controlling parameters on the particle rotational dynamics in viscoelastic flows. Besides the above potential fundamental contributions, it is also of practical importance to study the particle rotation in viscoelastic–inertial shear flows. One of the popularly used techniques to improve the efficiency of particle separation in microfluidics is using viscoelastic liquids with low viscosity and high elasticity (Lu & Xuan Reference Lu and Xuan2015; Li et al. Reference Li, McKinley and Ardekani2015; D'Avino et al. Reference D'Avino, Greco and Maffettone2017; Raoufi et al. Reference Raoufi, Mashhadian, Niazmand, Asadnia, Razmjou and Warkiani2019). In this regard, both fluid inertia and elasticity are important to the particle behaviours. Therefore, studying the elasto-inertial orientation of particles is instrumental in optimizing particle manipulation in microfluidic applications. Considering that viscoelastic-based particle manipulation is mainly utilized in biomedical areas, particles (such as RBC) are nearly neutrally suspended in the background fluids. The densities of these particles are generally similar to those of suspension fluids (Atwell et al. Reference Atwell, Badens, Charrier, Helfer and Viallat2022). Thus, the present study mainly focuses on neutrally buoyant particles. Moreover, the prolate spheroids suspended in viscoelastic fluids are widely encountered in various engineering applications, such as fibre-reinforced composite materials (Altan Reference Altan1990; Nabergoj, Urevc & Halilovič Reference Nabergoj, Urevc and Halilovič2022), papermaking processes (Lundell, Söderberg & Alfredsson Reference Lundell, Söderberg and Alfredsson2011) and the ‘rouleaux’ structure (a prolate spheroidal microstructure of RBCs) in blood (Fedosov et al. Reference Fedosov, Pan, Caswell, Gompper and Karniadakis2011; Kang Reference Kang2002). The orientation modes of these elongated particles can significantly affect the bulk properties of polymeric suspensions. This motivates the present study on the rotational dynamics of neutrally buoyant prolate spheroids in viscoelastic shear flows.
Finally, the particle shape and the characteristics of the particle surface also greatly affect the particle rotation in shear flows. For example, the critical Weissenberg numbers for the transition of the spheroid rotation modes are decreased by the particle aspect ratio (Gunes et al. Reference Gunes, Scirocco, Mewis and Vermant2008). Oblate spheroids behave differently with prolate spheroids in Newtonian (Rosén et al. Reference Rosén, Do-Quang, Aidun and Lundell2015b) and viscoelastic (Gauthier et al. Reference Gauthier, Goldsmith and Mason1971) shear flows. For a more complicated case, i.e. particles with irregular shapes, Daghooghi & Borazjani (Reference Daghooghi and Borazjani2018) found that the periodicity of the angular velocity could be broken by the non-asymmetry of irregularly shaped particles. This implies that the rotational dynamics of particles can be greatly altered by the particle shape. As for particles with a non-smooth surface, the local flow field near the particle surface is sensitive to the characteristics of the particle surface. Liu et al. (Reference Liu, Li, Ye and Liu2020) indicated that the rotation periods of highly permeable elliptical particles are smaller than those of particles with smaller porosity. In this case, the porous effect on the flow field should also be considered in the governing equations of fluid flow. Note that the coupled effect of fluid inertia and fluid elasticity on the rotation modes of the above complex spheroids should be studied based on the systematic knowledge of the single effect, which, however, is still developing. Considering this, the effects of particle shape and surface characteristics on particle rotational dynamics deserve to be studied in detail in future work.
The work is organized as follows. In § 2, we introduce the mathematical models and numerical methods for resolving the viscoelastic flow and particle rotation. Then the modulations of the three-dimensional (3-D) rotation modes by the interplay between fluid elasticity and inertial effects are analysed in § 3. Finally, conclusions are drawn in § 4.
2. Mathematical models and numerical methods
2.1. Governing equations
The mathematical models describing the present problem consist of the governing equations for viscoelastic fluid flow and particle rotation.
2.1.1. Viscoelastic fluid flow
For the fluid phase, the governing equations for incompressible and isothermal viscoelastic flows are written as
\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u} = 0, \end{gather}
\begin{gather}{\rho_f}\left( {\frac{{\partial \boldsymbol{u}}}{{\partial t}} + \boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{u}} \right) ={-} \boldsymbol{\nabla} p + \boldsymbol{\nabla} \boldsymbol{\cdot}\boldsymbol{\tau} ^s + \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{\tau}^p + {\boldsymbol{f}^{IB}}, \end{gather}
where 
$\boldsymbol {u}$ is the fluid velocity, 
${\rho _f}$ is the fluid density, 
$p$ is the pressure and 
${\boldsymbol {f}^{IB}}$ is the momentum force due to the fluid–particle interaction. To improve the computational stability of the viscoelastic flow simulation, the total stress is decomposed into the polymeric stress 
$\boldsymbol {\tau }^p$ and the solvent stress 
$\boldsymbol {\tau } ^s$ (Alves, Oliveira & Pinho Reference Alves, Oliveira and Pinho2021).
Generally, the solvent stress of viscoelastic fluid can be written as
\begin{equation} {\boldsymbol{\tau} ^s} = {{\mu _s}}\left( {\boldsymbol{\nabla} \boldsymbol{u} + {{\left( {\boldsymbol{\nabla} \boldsymbol{u}} \right)}^{\rm T}}} \right). \end{equation} The zero-shear-rate viscosity 
${\mu _0}$ and the solvent viscosity ratio 
$\beta$ are defined as follows:
\begin{gather} {\mu _0} \equiv {\mu _s} + {\mu _p}, \end{gather}
\begin{gather}\beta \equiv \frac{{{\mu _s}}}{{{\mu _0}}}, \end{gather}
where 
${\mu _s}$ and 
${\mu _p}$ represent the solvent and polymeric contributions to the zero-shear-rate viscosity, respectively.
The polymer stress can be further formulated as the following constitutive equation:
\begin{equation} {\boldsymbol{\tau} ^p}
+ \lambda \left( {\frac{{\partial {\boldsymbol{\tau}
^p}}}{{\partial t}} + \boldsymbol{u}
\boldsymbol{\cdot}\boldsymbol{\nabla} {\boldsymbol{\tau}
^p} - {\boldsymbol{\tau} ^p}
\boldsymbol{\cdot}\boldsymbol{\nabla} \boldsymbol{u} -
{{\left( {\boldsymbol{\nabla} \boldsymbol{u}} \right)}^{\rm
T}} \boldsymbol{\cdot} {\boldsymbol{\tau}^p} + \frac{\alpha }{{{\mu
_p}}}{\boldsymbol{\tau} ^p} \boldsymbol{\cdot}
{\boldsymbol{\tau} ^p}} \right) = {\mu _p}\left(
{\boldsymbol{\nabla} \boldsymbol{u} + {{\left(
{\boldsymbol{\nabla} \boldsymbol{u}} \right)}^{\rm T}}}
\right), \end{equation}
where 
$\lambda$ is the polymer relaxation time and 
$\alpha$ denotes the mobility factor representing the shear-thinning rheology of the polymeric solution. For a Giesekus-type fluid, the larger the mobility factor is, the more appreciable is the shear-thinning effect of the fluid; it is normally less than 0.5 to avoid unphysical solutions (Alves et al. Reference Alves, Oliveira and Pinho2021). Specifically, (2.5) reduces to the Oldroyd-B model when 
$\alpha =0$.
The polymer stress in the Oldroyd-B and Giesekus models can be determined by the conformation tensor 
$\boldsymbol{\mathsf{B}}$ based on the kinetic theory as
\begin{equation} {\boldsymbol{\tau} ^p} = \frac{{{\mu _p}}}{\lambda }\left( \boldsymbol{\mathsf{B}} - \boldsymbol{\mathsf{I}} \right), \end{equation}
where 
$\boldsymbol {I}$ is the identity matrix.
Then the conformation tensor-form constitutive equation can be described as
\begin{equation} \frac{{\partial
\boldsymbol{\mathsf{B}}}}{{\partial t}} + \boldsymbol{u}
\boldsymbol{\cdot}\boldsymbol{\nabla} \boldsymbol{\mathsf{B}} -
\boldsymbol{\mathsf{B}} \boldsymbol{\cdot} \left( {\nabla
\boldsymbol{u}} \right) - {\left(
{\boldsymbol{\nabla}\boldsymbol{u}} \right)^{\rm T}}
\boldsymbol{\cdot} \boldsymbol{\mathsf{B}} = \frac{1}{\lambda
}\left[ {\boldsymbol{\mathsf{I}} - \boldsymbol{\mathsf{B}} - \alpha \left(
{\boldsymbol{\mathsf{B}} \boldsymbol{\cdot} \boldsymbol{\mathsf{B}} -
2\boldsymbol{\mathsf{B}} + \boldsymbol{\mathsf{I}}} \right)} \right] .
\end{equation}
2.1.2. Particle rotation
Concerning the particle rotational motion, the following Euler equation is utilized:
\begin{equation} \frac{{\rm d}\left(\boldsymbol{I}_{p} \boldsymbol{\omega}_{p}\right)}{{\rm d} t}=\oint_{\varGamma_{p}} \boldsymbol{r} \times(\boldsymbol{\tau} \boldsymbol{\cdot} \boldsymbol{n}) \,{\rm d} s, \end{equation}
where 
$\boldsymbol {I}_{p}$ is the particle moment of inertia, 
$\boldsymbol {\omega }_{p}$ represents the particle angular velocity, 
$\varGamma _{p}$ is the particle surface, 
$\boldsymbol {r}$ is the position vector on the particle surface from the particle centre and 
$\boldsymbol {n}$ denotes the unit normal vector pointing outwards on the particle surface; 
$\boldsymbol {\tau }$ represents the hydrodynamic stress tensor acting on the particle as 
$\boldsymbol {\tau } = -p\boldsymbol{\mathsf{I}} + \boldsymbol {\tau } ^s + \boldsymbol {\tau }^p$. The integration of 
$\boldsymbol {\tau }$ accounts for the fluid–particle interaction
The immersed boundary method (IBM) is capable of resolving the effects of finite fluid inertia and fluid elasticity on particle rotation. Therefore, IBM is adopted to model the viscoelastic fluid–particle interaction in the present study. By integrating the momentum equation (2.2) and the Gauss theorem, the hydrodynamic torque acting on the particle can be rewritten as
\begin{equation} \oint_{\varGamma_{p}} \boldsymbol{r} \times(\boldsymbol{\tau} \boldsymbol{\cdot}\boldsymbol{n}) \,{\rm d} s=\int_{\varOmega_{p}} \boldsymbol{r} \times( \boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{\tau}) \,{\rm d} v = \frac{{\rm d}}{{\rm d} t} \int_{\varOmega_{p}} \rho_{f} \boldsymbol{r} \times \boldsymbol{u} \,{\rm d} v-\int_{\varOmega_{p}} \boldsymbol{r} \times \boldsymbol{f}^{I B} \,{\rm d} v, \end{equation}
where 
$\varOmega _{p}$ is the particle region bounded with surface 
$\varGamma _{p}$. In IBM, the momentum forcing term 
$\boldsymbol {f}^{IB}$ in (2.2) and (2.9) is used to satisfy the no-slip condition on the particle surface, which is spread from the fluid–particle interaction forcing term 
$\boldsymbol {F}_{IB}$
\begin{equation} \boldsymbol{f}^{I B}=\oint_{\varGamma_{p}} \boldsymbol{F}_{IB} \delta(\boldsymbol{x}-\boldsymbol{X}) \,{\rm d} s, \end{equation}
where 
$\delta$ is the Dirac delta function. Here, 
$\boldsymbol {X}$ denotes the positions of material Lagrangian points distributed on the particle surface. In the penalty IBM, the fluid–particle interaction forcing term 
$\boldsymbol {F}_{IB}$, acting on the particle surface from the fluid, is given as (Huang, Chang & Sung Reference Huang, Chang and Sung2011)
\begin{equation} \boldsymbol{F}_{IB} ={-} \kappa \left[ {\left( {{\boldsymbol{X}_{IB}} - \boldsymbol{X}} \right) + \Delta t\left( {{\boldsymbol{U}_{IB}} - \boldsymbol{U}} \right)} \right], \end{equation}
where 
$\kappa$ is a large penalty constant in IBM with 
$\kappa = 10^4$ in the present simulations; 
$\boldsymbol {X}_{IB}$ and 
$\boldsymbol {U}_{IB}$ represent the positions and velocities of the massless counterparts of the material Lagrangian points, respectively, and 
$\boldsymbol {U}$ denotes the velocities of the material Lagrangian points; 
$\Delta t$ is the time step.
To elaborate on the elasto-inertial effect on the particle rotational dynamics, the particle is fixed at the centre of the simulation domain, thus the translation of particles is neglected in this study. However, the particle rotation is not constrained, and the particle can freely rotate in all directions. The flow configuration investigated in the present work is sketched in figure 1, and the corresponding non-dimensional parameters are summarized as follows:
Figure 1. Schematic of a prolate spheroid in a viscoelastic shear flow.
(i) Particle Reynolds number,
${Re_p} = {{G{D_p^2}}/{{\nu _0}}}$, where $G$ is the constant shear rate of the flow, $D_p$ is the characteristic length of the particles, i.e. the major diameter of the particles, and ${\nu _0}$ is the zero-shear-rate kinematic viscosity of viscoelastic fluids. In the present simulation, the fluid shear rate $G$ and particle major-axis diameter $D_p$ are set as $G=1.0$ and $D_p=1.0$, respectively. The effect of fluid inertia is represented by the variation of the zero-shear-rate kinematic viscosity ${\nu _0}$.(ii) Stokes number,
$St={\rho _r}{Re_p}$, which represents particle inertia. Here, ${\rho _r}$ is the ratio between the particle and fluid densities, ${\rho _r}={\rho _p}/{\rho _f}$. In the present work, we focus on neutrally buoyant particles, i.e. ${\rho _r}=1.0$, and thus $St={Re_p}$ .(iii) Weissenberg number,
$Wi=\lambda G$, which represents the elastic effect of fluids.(iv) Elastic number,
$El=Wi/{Re_p}$, which quantifies the competition between fluid elastic and fluid inertial effects.(v) Particle aspect ratio,
$AR=a/b$, where $a$ and $b$ are the polar and equatorial radii of a spheroid, respectively.
2.2. Numerical methods
2.2.1. Viscoelastic flow solver
The governing equations of a viscoelastic fluid are discretized on the staggered grid using a finite-difference method. The pressure and conformation tensor are defined on the cell centre, while the velocity is located on the centre of the cell face, which is orthogonal to its stored velocity component. For spatial discretization of the governing equations, all terms are approximated by the second-order central difference scheme, except for the convective term in the constitutive equation, which is evaluated by a high-resolution scheme, i.e. the CUBISTA scheme that is often used in viscoelastic flow simulations (Pimenta & Alves Reference Pimenta and Alves2017). For temporal discretization of the momentum and constitutive equations, all terms are integrated in time by the second-order Crank–Nicolson scheme. The incremental form and staggered time (ST) scheme are utilized to treat the pressure gradient and elastic stress terms. In the ST scheme, the velocity was defined at the 
$n$ time level while the pressure and conformation tensor were defined at the 
$n+1/2$ time level. More details on the numerical method can be found in Li et al. (Reference Li, Huang, Xu and Zhao2022). With the above temporal and spatial discretization schemes, the discretized governing equations of viscoelastic flow can be written as
\begin{equation} D{\boldsymbol{u}^{n + 1}} = cb{c^n}, \end{equation}
\begin{align} &\frac{{{\boldsymbol{u}^{n + 1}}}}{{\Delta t}} + N{\boldsymbol{u}^{n + 1}} - \frac{\beta }{{2{Re}}}L{\boldsymbol{u}^{n + 1}} + G_f\delta p - \frac{{1 - \beta }}{{{WiRe_p}}}D\delta \boldsymbol{\mathsf{B}} \nonumber\\ &\quad = \frac{{{\boldsymbol{u}^n}}}{{\Delta t}} - G_f{p^{n - {1 /2}}} + \frac{\beta }{{2{Re} }}L{\boldsymbol{u}^n} + \frac{{1 - \beta }}{{WiRe_p}}D{\boldsymbol{\mathsf{B}}^{n - {1 / 2}}} +\boldsymbol{mbc}^{n + {1 / 2}}+\boldsymbol{f^{IB,n + {1 / 2}}}, \end{align}
\begin{align} &\frac{\delta\boldsymbol{\mathsf{B}}}{\Delta t} + \frac{1}{2} N_{u} \delta\boldsymbol{\mathsf{B}}+N_{u} \boldsymbol{\mathsf{B}}^{n-1/2}-\frac{1}{2}\delta\boldsymbol{\mathsf{B}}\boldsymbol{\cdot}\left(G_f \boldsymbol{u}^{n}\right)- \boldsymbol{\mathsf{B}}^{n-1/2} \boldsymbol{\cdot}\left(G_f \boldsymbol{u}^{n}\right) \nonumber\\ &\qquad -\frac{1}{2}\left(G_f \boldsymbol{u}^{n}\right)^{{\rm T}} \boldsymbol{\cdot} \delta\boldsymbol{\mathsf{B}}-\left(G_f \boldsymbol{u}^{n}\right)^{{\rm T}} \boldsymbol{\cdot} \boldsymbol{\mathsf{B}}^{n-1/2} \nonumber\\ &\qquad + \frac{1}{2Wi}\delta\boldsymbol{\mathsf{B}} + \frac{\alpha}{2Wi}\left(\delta\boldsymbol{\mathsf{B}} \boldsymbol{\cdot}\boldsymbol{\mathsf{B}}^{n-1/2}+\boldsymbol{\mathsf{B}}^{n-1/2} \boldsymbol{\cdot} \delta\boldsymbol{\mathsf{B}}-2\delta\boldsymbol{\mathsf{B}}\right)\nonumber\\ &\quad=\frac{1}{Wi}\left(\boldsymbol{\mathsf{I}}-\boldsymbol{\mathsf{B}}^{n-1/2}\right)- \frac{\alpha}{Wi}\left[\boldsymbol{\mathsf{B}}^{n-1/2} \boldsymbol{\cdot} \boldsymbol{\mathsf{B}}^{n-1/2}-2\boldsymbol{\mathsf{B}}^{n-1/2}+\boldsymbol{\mathsf{I}}\right], \end{align}
where 
$\delta p=p^{n+1/2}-p^{n-1/2}$, 
$\delta \boldsymbol{\mathsf{B}}=\boldsymbol{\mathsf{B}}^{n+1/2}-\boldsymbol{\mathsf{B}}^{n-1/2}$, 
$cbc$ is the discretization of the boundary condition in the continuity equation and 
$\boldsymbol {mbc}$ is the discretization of the boundary condition in the momentum equation. Further, 
$D$ represents the discretized divergence operator, 
$N$ represents the coefficient matrix of 
${\boldsymbol {u}^{n + 1}}$ in the discretized convective term of the momentum equation, 
$G_f$ denotes the discretized gradient operator, 
$L$ represents the discrete Laplacian operator and 
$N_u$ denotes the coefficient matrix of 
$\boldsymbol{\mathsf{B}}$ in the discretized convective term of the constitutive equation. Note that there is no need to prescribe a boundary condition for the constitutive equation.
By rearranging the discretized governing equations (2.12)–(2.14) in a monolithic matrix system, the pressure, conformation tensor and velocity can be decoupled from the viscoelastic flow system sequentially based on the approximate factorization of the system coefficient matrix. This decoupling procedure has been successfully applied to Newtonian (Kim, Baek & Sung Reference Kim, Baek and Sung2002; Pan, Kim & Choi Reference Pan, Kim and Choi2019) and viscoelastic (Li et al. Reference Li, Huang, Xu and Zhao2022) flow simulations. With this method, all quantities can be resolved in a projection framework without iteration.
2.2.2. Particle solver
For the particle phase, substituting equation (2.9) and (2.10) into the particle governing equation (2.8), the rotation of a particle is further described as follows:
\begin{equation} \frac{{{\rm d}\left( {{\boldsymbol{I}_p}{\boldsymbol{\omega} _p}} \right)}}{{{\rm d}t}} \approx{-} \sum_l^{{N_l}} {\boldsymbol{r} \times {\boldsymbol{F}_{IB,l}}} \Delta {s_l} + {\rho _f}\frac{{\rm d}}{{{\rm d}t}}\left( {\int_{{\varOmega _p}} {\boldsymbol{r} \times \boldsymbol{u}} \,{\rm d}v} \right) , \end{equation}
where 
$\Delta {s_l}$ is the surface area of each Lagrangian element on the particle surface and 
${N_l}$ is the total number of Lagrangian points.
The discretized particle rotation equation (2.15) is solved in the particle frame with the fourth-order Runge–Kutta scheme. The particle orientation is represented by quaternions (Goldstein Reference Goldstein1980), which are updated based on the particle angular velocity.
In the present study, the particle is located at the centre of a box with a size of 
$L \times H \times W$. The top and bottom boundaries of the computational domain move with a constant velocity in opposite directions. The velocity distribution of a simple shear flow is applied at the inlet boundary. Considering the fluid inertial effect, the convective outflow boundary is set at the outlet of the computational region. The periodic boundary is set in the spanwise direction. The size of the computational domain could affect the particle rotation in shear flows, thus, we compared the results calculated in the different computational domains to examine the domain-size effect on the particle rotation, as shown in figure 2. It can be seen that the evolutions of particle orientation and angular velocity calculated with two larger domains are in good agreement, while the results obtained using the small domain deviate slightly. Considering the computational cost, the domain size of 
$L \times H \times W = 8 \times 8 \times 4$ is chosen in the following simulations. The number of Eulerian grid points per major diameter of the particle is 32, thus the mesh resolution is 
$\varDelta = {1 /{32}}$. The time step is set as 
$\Delta t = 10^{-3}$ in all simulations. With this time step, the Courant–Friedrichs–Lewy numbers in all simulations satisfy 
${\rm {max}}\{u\Delta t /\varDelta,v\Delta t/\Delta x,w\Delta t/\varDelta \} \leqslant 0.2$, where 
$u, v, w$ denote three velocity components in the flow field. The validation of the present numerical methods is presented in Appendix A.
Figure 2. Comparisons of (a) azimuthal angle and (b) angular velocity vs time for a prolate with 
$AR = 2.0$, 
$Re_p = 0.1$ and 
$Wi = 2.0$ in different computational domain sizes.
3. Results and discussion
As mentioned in § 1, the single effect of fluid inertia or fluid elasticity on the rotation of prolate spheroids has been extensively studied. For fluid inertia, the orientation modes of prolate spheroids with 
$AR = 2$ (Yu, Phan-Thien & Tanner Reference Yu, Phan-Thien and Tanner2007; Huang et al. Reference Huang, Yang, Krafczyk and Lu2012) and 
$AR = 4$ (Rosén et al. Reference Rosén, Lundell and Aidun2014) have been comprehensively analysed in Newtonian shear flows. In Stokesian viscoelastic shear flows, the rotational dynamics of prolate spheroids (
$AR = 4$) is also reported in simulations (D'Avino et al. Reference D'Avino, Hulsen, Greco and Maffettone2014) and experiments (
$AR = 2\sim 6$) (Johnson et al. Reference Johnson, Salem and Fuller1990). To clearly elaborate on the different orientation modes of prolate spheroids induced by the elasto-inertial effect, we focus on the prolate spheroids with the same aspect ratios (
$AR = 1$, 
$2$ and 
$4$) used in the earlier studies on the single effect.
Considering the finite fluid inertia in the practical applications related to the dynamics of particles in viscoelastic fluids, we set the particle Reynolds number as 
$Re_p = 0.1$ and 
$Re_p = 10.0$ in the present study. These specific values of 
$Re_p$ are chosen mainly for the fluid inertia in the manipulation of bioparticles in microfluidics. Lu & Xuan (Reference Lu and Xuan2015) and Lim et al. (Reference Lim, Ober, Edd, Desai, Neal, Bong, Doyle, McKinley and Toner2014) experimentally studied the elasto-inertial focusing of particles in viscoelastic flows with different fluid inertia, i.e. bulk Reynolds numbers 
$Re_H =UH/{\nu _0}= 4.86$ and 
$105.0$ (
$U$ is the bulk velocity and 
$H$ denotes the height of microchannel). Correspondingly, the shear Reynolds numbers of particles in their experiments are roughly estimated as 
$Re_p$ about 
$O(0.1) \sim O(10.0)$. Thus, the present study mainly focuses on the cases with weak and moderate fluid inertia, i.e. 
$Re_p = 0.1$ and 
$Re_p = 10.0$.
In this section, the rotational dynamics of particles in viscoelastic shear flows with finite fluid inertia is investigated numerically. To investigate the effect of fluid elasticity on the particle rotation in the shear plane, we first focus on the case with weak fluid inertia (
$Re_p = 0.1$) in § 3.1. Then, with moderate fluid inertia (
$Re_p = 10.0$), the orientation modes and drift of particle 3-D orbits induced by the competition between fluid elasticity and fluid inertial effects are studied in § 3.2.
3.1. Particle rotation in the shear plane
3.1.1. Effect of fluid elasticity
To understand the mechanism of the reduction of the particle rotation rate caused by fluid elasticity, we look into the viscoelastic shear flow with weak fluid inertia (
$Re_p = 0.1$). The rheological parameters in the present viscoelastic shear flows are set as 
$\beta = 0.0909$ and 
$\alpha = 0.2$, which are consistent with those in the earlier work (D'Avino et al. Reference D'Avino, Hulsen, Greco and Maffettone2014). The evolutions of the azimuthal angle of prolate spheroids are shown in figure 3, in which, compared with the Newtonian case (
$Wi = 0$), fluid elasticity significantly increases the particle rotation period in viscoelastic flows. The rotation period of particles with large aspect ratios is more obviously changed by fluid elasticity. For 
$AR = 4.0$, the particle can remain in a motionless state, which reveals that fluid elasticity stabilizes the particle rotation. In addition, we further analyse the effect of fluid elasticity on the particle angular velocity at different orientations, and the results are shown in figure 4.
Figure 3. Evolution of azimuthal angle of particle with different aspect ratios: (a) 
$AR=1.0$; (b) 
$AR=2.0$; (c) 
$AR=4.0$.
Figure 4. Particle angular velocity vs orientation in the polar coordinate system. The radial coordinate represents particle angular velocity and the polar angle denotes the azimuthal angle between the particle symmetry axis and the streamwise direction: (a) 
$AR=1.0$; (b) 
$AR=2.0$; (c) 
$AR=4.0$.
For spherical particles, figure 4 suggests that spherical particles rotate with a constant angular velocity in viscoelastic fluids, which is similar to that in a Newtonian case. The sphere rotation rate is remarkably reduced by fluid elasticity, which is consistent with the results reported by Snijkers et al. (Reference Snijkers, D'Avino, Maffettone, Greco, Hulsen and Vermant2011), and spheroidal particles exhibit more peculiar rotation behaviours in viscoelastic shear flows. The particles with different aspect ratios are affected by fluid elasticity in different ways. For particles with small eccentricity (
$AR = 2.0$), figure 4(b) shows that the curve of the particle angular velocity at different orientations in a stronger viscoelastic fluid (
$Wi = 4$) is bounded by that in a weaker viscoelastic fluid (
$Wi = 2$). This reveals that the particle angular velocities at all orientations are decelerated by fluid elasticity. However, for particles with large eccentricity (
$AR = 4.0$), the influence of fluid elasticity on the particle angular velocity becomes orientation dependent. When the particle orients toward the flow direction, the particle angular velocity is slightly decreased by fluid elasticity, while it is increased when the particle is normal to the flow direction (seen in figure 4c). More interestingly, when the fluid elasticity further increases, the particle with 
$AR = 4.0$ reaches a steady alignment in the streamwise direction.
Figure 5 shows the variations of total torque during the particle rotation. It can be seen that fluid elasticity breaks the symmetry of the particle rotation process observed in Newtonian flow (blue line in figure 5). The particle deceleration takes a longer time than the acceleration. More quantitatively, the period of particle deceleration is approximately twice that of acceleration, which could be caused by the coupled effect of stress relaxation and the transient shear-thinning rheology (Varchanis et al. Reference Varchanis, Tsamopoulos, Shen and Haward2022) of viscoelastic fluids. During the particle deceleration, the local shear rate on the particle increases, except for the tip area of the particle. With the transient shear-thinning effect, the decreased local viscosity near the particle would lead to an attenuated drag force (less energy) on the particle from the surrounding fluids, and thus the particle rotation rate is hindered during its deceleration. This will strengthen the symmetry breaking of the particle rotation process.
Figure 5. Evolution of total hydrodynamic torque acting on a particle with 
$AR=2.0$. The torque in the shaded area represents the driving torque for particle rotation. 
$T=Gt/2{\rm \pi}.$
Based on the kinematic theory, the conformation tensor 
$\boldsymbol{\mathsf{B}}$ is defined as (Bird et al. Reference Bird, Curtiss, Armstrong and Hassager1987)
\begin{equation} \boldsymbol{\mathsf{B}} = \frac{{\left\langle \boldsymbol{QQ} \right\rangle }}{{Q_{eq}^2}}, \end{equation}
where 
$\boldsymbol {Q}$ is the end-to-end vector in the dumbbell model of polymer molecules, and 
$\boldsymbol {Q}_{eq}$ represents 
$\boldsymbol {Q}$ at the polymer equilibrium state. From (3.1), the conformation tensor can quantify the relative deformation of the polymer molecule in the flow field.
According to the conformation tensor field shown in figure 6, it is found that the polymer deformation induced by the flow field depends on the particle orientation. When the particle symmetry axis changes from being perpendicular (
$y$ axis) to parallel (
$x$ axis) to the flow direction, 
$B_{ii}$ becomes smaller. This represents the deformation of polymer being reduced and partially recovered (3.1) when the particle aligns its symmetry axis along the flow direction. The elastic torque acting on the particle is associated with the polymer deformation (as shown in (2.6)), thus the elastic stress will decrease during the particle deceleration process. However, the stress relaxation effect (due to the relaxation time 
$\lambda$) of the viscoelastic fluid makes the response of the elastic stress hysteretic to the strain variation (Ewoldt & Saengow Reference Ewoldt and Saengow2022). Therefore, the decay of the elastic stress is retarded to the recovery of deformed polymer. Such a decaying characteristic of the elastic stress makes the particle experience a longer period of resisting hydrodynamic torque, thus the particle angular velocity evolves asymmetrically, as shown in figure 5.
Figure 6. Contour of conformation tensor around particle with 
$Wi = 4.0$, 
$AR = 2$: (a) and (d) 
$B_{xx}$; (b) and (e) 
$B_{yy}$; (c) and (f) 
$B_{zz}$.
Physically, the polymer is generally stretched in shear flows and forms stretched microstructures (seen in figure 6) in the flow field; these microstructures of polymer would create tension along the streamlines (Ewoldt & Saengow Reference Ewoldt and Saengow2022). By comparing the distributions of the conformation tensor around particles with different orientations in figure 6, we find that the deformation of polymer is more obvious when the particle is perpendicular to the flow direction. This indicates that it is more difficult for particles to overcome the streamline tension when they are perpendicular to the flow direction. Thus, the orientation-dependent polymer deformation might also bring asymmetry to the particle rotation process shown in figure 5.
On the other hand, the reduction of the particle rotation rate in viscoelastic shear flows is also linked to the above stretched structure of polymer in the flow field. From figure 6, it is found that the maximum of the conformation tensor (
$B_{xx}$ in figure 6a,d) mainly locates around the particle tip. The distribution of the conformation tensor shows the ‘sheet-like’ structure of polymer deformation in the particle upstream, especially for the distribution of 
$B_{xx}$ in figure 6(a). Additionally, figure 7 shows the distribution of elastic stress on the particle surface when the particle aligns along the flow direction. Similar to figure 6, the strong elastic stress also mainly locates near the particle tip. The above distributions of the conformation tensor and elastic stress reveal that the polymer is highly stretched near the particle tip. When the particle rotates, the streamlines near the particle surface will be changed, and the streamline tension generated by the stretched structures of polymer induce an opposite torque to hinder the particle rotation, causing a reduction of the particle rotation rate in viscoelastic shear flows, as shown in figures 4 and 5.
Figure 7. Pressure and elastic stress contours on the particle surface (
$Wi = 4.0$, 
$AR = 2$): (a) pressure; (b–g) the six independent components of the elastic stress tensor.
3.1.2. Effect of solvent viscosity ratio and mobility factor
In addition to the effect of fluid elasticity (
$Wi$), other rheological factors, including the solvent viscosity ratio and the mobility factor, also affect the flow characteristics and particle dynamics.
Figure 8 shows the particle angular velocities in viscoelastic shear flows with different solvent viscosity ratios. The solvent viscosity ratio reflects the contribution of solvent to the total zero-shear-rate viscosity of the viscoelastic fluid solution. From (2.6), it can be found that the smaller the solvent viscosity ratio is, the stronger the elastic stress is. Figure 8(a) indicates that the solvent viscosity ratio has little influence on the relationship between particle angular velocity and orientation. However, figures 8(b) and 8(c) obviously show that the evolutions of particle orientation and angular velocity can be changed by the solvent viscosity ratio. Figure 8(b) shows that the particle rotation period decreases monotonically with the viscosity ratio. With increasing solvent viscosity ratio, the elastic stress becomes weaker, and the particle angular velocity increases, thus the period of particle rotation decreases.
Figure 8. Effect of solvent viscosity ratio on particle rotation (
$Wi = 2.0$, 
$AR = 2.0$): (a) angular velocity vs particle orientation; (b) azimuthal angle; (c) angular velocity.
Compared with the influence of fluid elasticity (
$Wi$) on the particle angular velocity (figure 5), the solvent viscosity ratio shows a more peculiar effect. From figure 8(c), we find that, with increasing solvent viscosity ratio, the magnitude of the maximum angular velocity decreases, while that of the minimum angular velocity increases.
Moreover, the shear-thinning and extension-hardening rheology, as two additional important rheological characteristics of polymeric solution, can be described by the Giesekus model. Previous studies have shown that the migration dynamics of particles is strongly affected by the mobility factor (Li et al. Reference Li, McKinley and Ardekani2015). In this paper, we examine the effect of the mobility factor on the particle rotation behaviour, as shown in figure 9.
Figure 9. Effect of mobility parameter on particle rotation (
$Wi = 2.0$, 
$AR = 2.0$): (a) angular velocity vs particle orientation; (b) azimuthal angle; (c) angular velocity.
From figures 9(a) and 9(c), it is found that the mobility factor mainly affects the maximum angular velocity of the particle. Specifically, the magnitude of the maximum angular velocity is attenuated by the mobility factor, while the minimum angular velocity is almost the same. Unlike the solvent viscosity ratio, the particle rotation period is a non-monotonic function of the mobility factor. The mobility factor affects viscoelastic flows in two main regards (Li et al. Reference Li, McKinley and Ardekani2015): (i) reducing the elastic stress; and (ii) strengthening the fluid inertial effect through decreasing the apparent viscosity of fluids. Compared with the viscoelastic shear flow with 
$\alpha = 0.0$ (Oldroyd-B fluid), the elastic stress is weaker in the flows with 
$\alpha > 0.0$, and thus the particle rotates faster. For example, when 
$\alpha =0.2$, the particle rotation period is less than that in an Oldroyd-B fluid. However, when 
$\alpha =0.4$, the particle rotation slows down again. This non-monotonic relationship between the particle rotation period and the mobility factor is related to the shear-thinning and extension-hardening rheology of viscoelastic fluids. The role of the shear-thinning rheology in the particle rotation can be explained by the effect of fluid inertia, which has been studied systematically in Newtonian shear flows (Mao & Alexeev Reference Mao and Alexeev2014).
On the other hand, the extension-hardening rheology of viscoelastic fluids is suppressed by increasing the mobility factor (Giesekus Reference Giesekus1982). Moreover, Debbaut & Crochet (Reference Debbaut and Crochet1988) indicated that the extension-hardening effect could increase the drag on the sphere in viscoelastic fluids. In the present flow system, compared with the case of 
$\alpha =0.2$, the extension-hardening effect in the flow with 
$\alpha =0.4$ is weaker, and thus the hydrodynamic torque exerted on the particle is decreased due to the attenuated drag force of the particle. Therefore, the particle rotation period is enlarged with 
$\alpha =0.4$. The above results indicate that there exists a critical 
$\alpha$ to minimize the reduction of the particle rotation rate in viscoelastic shear flows.
3.2. Three-dimensional rotation modes of particle in viscoelastic–inertial shear flow
The 3-D rotation and orientation modes of particles have been extensively studied in Newtonian shear flows (Mao & Alexeev Reference Mao and Alexeev2014; Rosén et al. Reference Rosén, Lundell and Aidun2014, Reference Rosén, Do-Quang, Aidun and Lundell2015a) or viscoelastic shear flows neglecting fluid inertia (Stokes flow) (D'Avino et al. Reference D'Avino, Hulsen, Greco and Maffettone2014). However, the coupled effect of fluid inertia and viscoelasticity on the rotation modes of particles has not been explored. Therefore, in this section, the rotation modes of a prolate particle (
$AR = 4.0$) in the viscoelastic shear flow at 
$Re_p = 10.0$ are studied numerically. The mobility factor 
$\alpha$ and the solvent viscosity ratio 
$\beta$ are set as 
$\alpha =0.2$ and 
$\beta = 0.0909$, respectively.
3.2.1. Tumbling mode with weak fluid elasticity
Firstly, we analyse the particle rotation modes in viscoelastic shear flows with weak fluid elasticity. The tumbling mode of the prolate particle is shown in figure 10 and we find that, when fluid elasticity is weak, the particle spirals out to the shear plane and eventually tumbles around the vorticity direction. This particle rotation mode is similar to that in Newtonian shear flow with the same fluid inertial effect (
$Re_p = 10.0$). According to the analysis by Rosén et al. (Reference Rosén, Lundell and Aidun2014, Reference Rosén, Do-Quang, Aidun and Lundell2015a), particle inertia induces the tumbling mode in the shear plane. Thus, the present tumbling mode of the particle in weakly viscoelastic shear flow is also caused by particle inertia.
Figure 10. Tumbling mode of particle in viscoelastic shear flows with weak fluid elasticity: (a) 
$El=0$; (b) 
$El=0.005$; (c) 
$El=0.01$. Panels (a i–c i) show the 3-D trajectory of particle tip; (a ii–c ii) show the coordinates of particle symmetry axis; (a iii–c iii) show the projection of 3-D trajectory of particle tip on the shear plane (
$x$–
$y$ plane); (a iv–c iv) show the particle angular velocities (
$\omega '_{p=x,y,z}$) in the particle frame. The filled and open circles in (a i–a iii) and (c i–c iii) denote the initial and final positions of the particle, respectively.
In addition, the particle orbit drift is also modified by fluid elasticity. The particle orbit drift can be quantified by the orbit parameter 
$C_b$ and the orbit drift rate 
$c^\prime$. These two parameters have been widely used to analyse the particle orbit drift in Newtonian shear flows (Lundell & Carlsson Reference Lundell and Carlsson2010; Mao & Alexeev Reference Mao and Alexeev2014; Rosén et al. Reference Rosén, Lundell and Aidun2014). The normalized orbit parameter 
$C_b$ is formulated as follows (Mao & Alexeev Reference Mao and Alexeev2014):
\begin{gather} {C_b} = \frac{C}{{C + 1}}, \end{gather}
\begin{gather}C = AR^{ - 1}\tan \theta \sqrt {\left( AR^2\sin^2\phi + \cos^2\phi \right)} , \end{gather}
where 
$\theta$ and 
$\phi$ are the polar angle and azimuthal angle of the particle symmetry axis, respectively.
The rate of orbit drift is quantified by the parameter 
$c^\prime$, defined as (Lundell & Carlsson Reference Lundell and Carlsson2010)
\begin{equation} c^\prime = \frac{{2\ln \left( {{C_{\phi ={-} {{\rm \pi} / 2}}}/{C_{\phi ={-} {{3{\rm \pi} } / 2}}}} \right)}}{{{T_J}}} ,\end{equation}
where 
${T_J}$ is the period of the Jeffery orbit (Jeffery Reference Jeffery1922). Herein, the above two orbit parameters are also utilized to evaluate the effect of fluid elasticity on the particle orbit drift, as shown in figure 11.
Figure 11. Effect of weak fluid elasticity on the particle orbit drift: (a) orbit parameter; (b) orbit drift rate. The initial particle orientation is 
$(\phi,\theta,\psi )_0 =(0.5{\rm \pi}, 0.1{\rm \pi}, 0)$ and 
$Re_p = 10.0$. Red dashed line in (b) is a fitting curve.
Figure 11(a) shows the evolution of the particle orbit parameter 
$C_b$. Compared with the Newtonian case (
$El = 0$), the time required for a particle to drift to the shear plane (
$C_b = 1.0$) is obviously increased. This means that fluid elasticity slows down the particle drift process. The reason is that the drift direction of the particle orbit induced by weak fluid elasticity is opposite to that driven by particle inertia: weak fluid elasticity drives the particle to the vorticity direction, while particle inertia makes the particle spiral out to the shear plane (seen in figure 10). Therefore, fluid elasticity would weaken the effect of particle inertia on the particle orbit drift. In figure 11, the particle inertia is still dominant in viscoelastic shear flow due to the weak fluid elasticity, and thus the particle finally tumbles in the shear plane. From figure 11(a), it is found that the particle orbit parameter 
$C_b$ varies nonlinearly with time, which is similar to that in the Newtonian case. Specifically, the closer the particle is to the shear plane, the more slowly the particle orbit drifts.
To further quantitatively describe the effect of fluid elasticity on the drift rate of the particle orbit, figure 11(b) shows the relation between the particle orbit drift rate and the elastic number, 
$El$. In figure 11(b), the orbit drift rate is negatively correlated with 
$El$, indicating fluid elasticity attenuates the particle orbit drift rate. The fitting curve in figure 11(b) reveals that the particle orbit drift rate is approximately linearly correlated with the elastic number within the ranges of 
$El$ considered in the present study.
3.2.2. Asymmetric-kayaking mode with moderate fluid elasticity
In this section, we focus on the particle rotation behaviour in viscoelastic shear flows with moderate fluid elasticity. In this situation, the final rotation mode of the particle is determined by the competition among the fluid inertia, particle inertia and fluid elasticity.
Figure 12 shows the 3-D trajectories of the particle tip at two different initial orientations, i.e. 
$(\phi,\theta,\psi )_0 = (0.5{\rm \pi}, 0.4{\rm \pi}, 0)$ and 
$(0.5{\rm \pi}, 0.1{\rm \pi}, 0)$. As a contrast, the particle rotation mode induced by weak fluid elasticity (
$El = 0.01$) is also included in figure 12(a). The comparisons between figures 12(a) and 12(b–d) reveal that, with increasing fluid elasticity, the drift direction of particle orbit is changed: the particle spirals toward a specific closed orbit between the vorticity axis and shear plane, and finally rotates along a Jeffery-like orbit, which depends upon the fluid elasticity. This peculiar rotation mode, caused by the interplay between fluid elasticity and inertial effects, is similar to the kayaking mode (Rosén et al. Reference Rosén, Lundell and Aidun2014) in Newtonian shear flows.
Figure 12. Trajectory of particle tip in viscoelastic flows with different elastic numbers: (a) 
$El=0.01$; (b) 
$El=0.03$; (c) 
$El=0.05$; (d) 
$El=0.1$. Different colours denote different initial particle orientations.
To quantify the modulations of particle orbit drift by moderate fluid elasticity, figure 13 shows the evolution of the particle orbit parameter 
$C_b$ under moderate fluid elasticity (
$El = 0.03 \sim 0.1$). Here, we find that the actual drift direction of the particle orbit is determined by the relative position of the particle initial orientation to the final equilibrium orbit. The particle always migrates to the equilibrium orbit despite different initial orientations. This observation indicates that this final equilibrium orbit is a stable limit cycle in phase space. In the Newtonian case, there exists an unstable limit cycle between the shear plane and vorticity direction (Rosén et al. Reference Rosén, Lundell and Aidun2014). Figure 13 also shows that the particle orbit parameter is a nonlinear function of time. The drift rate of the particle orbit slows down when the particle approaches the final equilibrium orbit. Different from the case with weak fluid elasticity (figure 11), the moderate fluid elasticity accelerates the drifting process of the particle orbit. This means that the particle can be quickly attracted to the equilibrium orbit through increasing fluid elasticity.
Figure 13. Evolution of particle orbit parameter in viscoelastic shear flow with moderate fluid elasticity. The red filled and open circles at 
$t=0$ denote two different initial orientations.
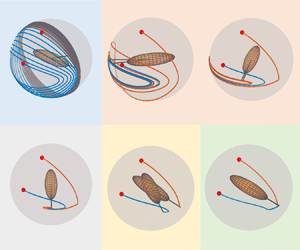
Figure 14 shows the final equilibrium orbits of particles at different elastic numbers, 
$El$. As shown in figure 12, in viscoelastic shear flows with moderate fluid elasticity, the particle eventually rotates along a Jeffery-like orbit periodically. However, the shape of the present equilibrium orbit is different from the Jeffery orbit (Jeffery Reference Jeffery1922) in Newtonian flows, the projection of Jeffery orbits on the shear plane is axisymmetric to the 
$x$ or 
$y$ axis (the green circle in figure 14), while the projection of the present equilibrium orbit is asymmetric about the 
$x$ or 
$y$ axis. Therefore, referring to the kayaking rotation mode of the particle in Newtonian shear flows, the present rotation mode associated with the asymmetric equilibrium orbit could be named the asymmetric-kayaking mode. Figure 14 also reveals that, with increasing fluid elasticity, the deviation between the present equilibrium orbit and the Jeffery orbit is more obvious. Thus, the asymmetry of the equilibrium orbit is more remarkable.
Figure 14. Steady asymmetric-kayaking mode in viscoelastic flows with different elastic numbers: (a) 
$El=0.03$; (b) 
$El=0.05$; (c) 
$El=0.1$. The green line is the Jeffery orbit (Jeffery Reference Jeffery1922).
Moreover, the sensitivities of the tumbling and asymmetric-kayaking modes to the rheological parameters (
$\alpha$ and 
$\beta$) of viscoelastic fluids are demonstrated in figures 15 and 16. In figure 15(a), it is found that, in weakly viscoelastic flows with different mobility factors 
$\alpha =0.0$, 
$0.2$ and 
$0.4$, the spheroid finally shows the tumbling mode in the shear plane, and the orbit drift rates are almost unchanged by 
$\alpha$. Similarly to the mode observed in figure 14(c), when the fluid inertia and fluid elasticity are comparable, particle rotation remains in the asymmetric-kayaking mode in viscoelastic shear flows with different 
$\alpha$. However, the final equilibrium orbit of the spheroid is determined by 
$\alpha$: the larger 
$\alpha$ is, the flatter the shape of the steady orbit (figure 15c).
Figure 15. Effect of mobility factor on the rotation modes of spheroid in shear flow with weak (
$El=0.005$) and moderate (
$El=0.1$) fluid elasticities, 
$AR=4.0$, 
$Re_p=10.0$, 
$\beta =0.0909$: orbit parameter at 
$El=0.005$ (a) and 
$El=0.1$ (b); (c) equilibrium asymmetric-kayaking mode at 
$El=0.1$.
Figure 16. Effect of solvent viscosity ratio on the rotation modes of spheroid in shear flow with weak (
$El=0.005$) and moderate (
$El=0.1$) fluid elasticities, 
$AR=4.0$, 
$Re_p=10.0$, 
$\alpha =0.2$: orbit parameter at 
$El=0.005$ (a) and 
$El=0.1$ (b); (c) equilibrium asymmetric-kayaking mode at 
$El=0.1$.
Figure 16 shows the effect of the solvent viscosity ratio (
$\beta =0.0454$, 
$0.0909$ and 
$0.1818$) on the spheroid rotation modes. Similarly to the mobility factor, the rotation modes of the spheroid are slightly affected by the solvent viscosity ratio. The prolate spheroid eventually shows the tumbling mode and asymmetric-kayaking mode when 
$El=0.005$ and 
$El=0.1$, respectively. Within the present range of 
$\alpha$ and 
$\beta$, compared with the solvent viscosity ratio, the rotation modes are more sensitive to the mobility factor.
Finally, from results in § 3.2.1 (weak fluid elasticity) and § 3.2.2 (moderate fluid elasticity), we conclude that there exists a critical elastic number, 
$El_c$, governing the transitions of particle rotation modes in viscoelastic shear flows with 
$Re_p= 10.0$: (i) when 
$El < El_c$, the particle inertia is dominant and the particle exhibits the ‘tumbling mode’ in the shear plane; (ii) with 
$El > El_c$, the fluid elasticity and inertial effects become comparable, the competition makes particle rotate in the ‘symmetric-kayaking mode’. In the present simulation, this critical elastic number is estimated numerically as 
$El_c \sim 0.02$, as shown in figure 17. This means that, with the present simulation parameters, once the elastic number exceeds 0.02, the final particle rotation mode begins to be primarily affected by fluid elasticity. Note that the present 
$El_c$ is of the same order as the critical elastic number governing the elasto-inertial lateral migration of spherical particles (
$El_c\sim 0.01$) (Li et al. Reference Li, McKinley and Ardekani2015). This further indicates that when the elastic number in viscoelastic flow systems reaches 
$O(0.01)$, the effect of fluid elasticity on both the migration and rotation of particles has to be considered.
Figure 17. Polar angle of the intersection point of the equilibrium orbit and 
$y$ axis (
$\phi = {\rm \pi}/2$).
3.2.3. Rotation modes induced by strong fluid elasticity
In this section, we examine the particle rotation modes in viscoelastic shear flows with strong fluid elasticity. As shown in figure 18, we find that, with increasing fluid elasticity, the particle shows a rolling mode between the flow and vorticity directions, a bi-stable orientation mode and a flow-alignment mode. Except for 
$El = 0.4$ (figure 18b), the final orientations of the particle released from different initial positions are consistent (figure 18a,c), which indicates that the rolling mode in the flow–vorticity plane (figure 18a) and the flow-alignment mode (figure 18c) are both stable (stable fixed point in phase space). Interestingly, the bi-stable orientation mode reported in the experiments (Johnson et al. Reference Johnson, Salem and Fuller1990; Gunes et al. Reference Gunes, Scirocco, Mewis and Vermant2008) and numerical simulations in viscoelastic shear flow with zero fluid inertia (D'Avino et al. Reference D'Avino, Hulsen, Greco and Maffettone2014) is also found in the present viscoelastic shear flow with finite fluid inertia. Overall, the particle orientation modes under the present flow conditions are similar to those in viscoelastic shear flows without fluid and particle inertia. This indicates that, once fluid elasticity becomes fully dominant in a flow system, the particle rotational dynamics in viscoelastic–inertial shear flows could still be predicted by the results obtained with the Stokesian flow assumption.
Figure 18. Particle rotation modes induced by the strong fluid elasticity: (a) 
$El=0.3$; (b) 
$El=0.4$; (c) 
$El=0.5$. The different colours of particle trajectories in (a i–c i) and (a ii–c ii) denote particles released from different initial orientations 
$(\phi,\theta,\psi )_0 =(0.5{\rm \pi}, 0.4{\rm \pi}, 0)$ and 
$(0.5{\rm \pi}, 0.1{\rm \pi}, 0)$, respectively. The solid and dashed lines in (a iii–c iii) and (a iv–c iv) represent the coordinates and angular velocities (
$\omega '_{p=x,y,z}$) of the particles with the above two different initial orientations.
When the fluid elasticity becomes dominant in the flow system, the rheological properties of viscoelastic fluids are highly dependent on 
$\alpha$ and 
$\beta$. Both figures 19 and 20 reveal that 
$\alpha$ and 
$\beta$ significantly affect the particle orientation modes in the shear flow with strong fluid elasticity. As shown in figure 19, with increasing 
$\alpha$, the fluid elasticity is suppressed, thus the equilibrium orientation of the particle is approaching the vorticity direction (figure 19b,c). When 
$\alpha$ increases to 
$\alpha = 0.4$, the attenuated fluid elasticity is not dominant in the flow system, then the comparable fluid inertia and fluid elasticity together induce the asymmetric-kayaking mode, which is similar to the rotation mode observed in the shear flow with the moderate fluid elasticity (figure 12).
Figure 19. Effect of mobility factor on the orientation modes of prolate spheroid in the shear flow with strong (
$El=0.3$) fluid elasticity, 
$AR=4.0$, 
$Re_p=10.0$, 
$\beta =0.0909$. (a) 
$\alpha=0$, (b) 
$\alpha=0.2$, (c) 
$\alpha=0.4$.
Figure 20. Effect of solvent viscosity ratio on the orientation modes of a prolate spheroid in the shear flow with strong (
$El=0.3$) fluid elasticity, 
$AR=4.0$, 
$Re_p=10.0$, 
$\alpha =0.2$. (a) 
$\beta=0.0454$, (b) 
$\beta=0.0909$, (c) 
$\beta=0.1818$.
Figure 20 shows the dependence of the orientation modes of the prolate spheroid on the solvent viscosity ratio. As discussed in § 3.1, the smaller the solvent viscosity ratio is, the stronger the fluid elastic stress is. From this point of view, as 
$\beta$ varies from 
$\beta = 0.0454$ to 
$\beta = 0.1818$, the fluid elasticity attenuates in the flow system, thus the prolate particle finally exhibits the flow-alignment state (figure 20a), the inclined-rolling mode between the flow and vorticity directions (figure 20b) and the asymmetric-kayaking mode (figure 20c). It is worthwhile noting that, although these two rheological parameters can modulate the critical elastic number 
$El_c$, which governs the transition of particle rotation modes, the mechanism behind the transitions of particle rotation modes is consistent with that discussed in previous sections.
On the other hand, the fluid inertia can also modulate the particle rotation modes in the viscoelastic shear flow with strong fluid elasticity. Figure 21 shows that, with increasing fluid inertia (
$Re_p$), the particle gradually approaches the shear plane. When 
$Re_p < 8.0$, the fluid elasticity is dominant in the flow system, and thus the particle orientation modes are similar to those in the viscoelastic flow with negligible fluid inertia (
$Re_p =0.1$). However, the angle between the particle symmetry axis and the shear plane is changed due to the fluid inertia (figure 21a–c). When the fluid inertia becomes more dominant (
$Re_p >13.0$), the particle is driven to the shear plane and finally reaches a steady state, which is similar to the rotation mode of the particle in a Newtonian shear flow with large fluid inertia (
$Re_p \sim 100.0$) (Rosén et al. Reference Rosén, Lundell and Aidun2014). The steady angle between the particle symmetry axis and flow direction is slightly modulated by the higher 
$Re_p =40.0$ and 
$Re_p =50.0$. Note that, different from the Newtonian case, such a motionless state of a particle in the shear plane within the present elasto-inertial shear flow can be realized with moderate fluid inertia (
$Re_p \sim 13.0$). This implies that it is convenient to manipulate the orientations of non-spherical particles in elasto-inertial flows with moderate fluid inertia, which corresponds to a small pressure gradient (less energy) used to operate microfluidic devices.
Figure 21. Effect of fluid inertia on the orientation modes of a prolate spheroid with 
$AR=4.0,El=0.4$. The initial orientation of particle is 
$(\phi,\theta,\psi )_0 =(0.5{\rm \pi}, 0.4{\rm \pi}, 0)$. (a) 
$Re_{p} = 0.1$, (b) 
$Re_{p} = 5.0$, (c) 
$Re_{p} = 8.0$, (d) 
$Re_{p} = 13.0$, (e) 
$Re_{p} = 40.0$, (f) 
$Re_{p} = 50.0$.
Finally, according to results in § 3.2, an overall picture of rotation modes for a neutrally buoyant prolate particle in viscoelastic–inertial shear flows is plotted in figure 22. Compared with the observed particle orientation modes in viscoelastic shear flows with zero fluid and particle inertia (D'Avino et al. Reference D'Avino, Hulsen, Greco and Maffettone2014), the rotational and orientational dynamics of neutrally buoyant particles in the present viscoelastic shear flows is more complicated. Figure 22 shows four critical elastic numbers that classify particle rotation modes. In contrast to the earlier studies on the viscoelastic shear flow system within the Stokesian regime, there are two additional critical elastic numbers given in the present flow system. Consequently, a newly observed rotation mode (asymmetric-kayaking mode) induced by the competition among the fluid elasticity, fluid inertia and particle inertia, occurs in the present particle-laden viscoelastic flow system with finite fluid inertia (
$Re_p= 10.0$).
Figure 22. Illustration of multi-orientation modes of a neutrally buoyant prolate particle (
$AR=4.0$) in viscoelastic shear flow with finite fluid inertia (
$Re_p=10.0$). Here, 
$El_{c1\sim c4}$ are four critical elastic numbers that classify particle rotation modes.
In a summary, figure 22 clearly reveals that the neutrally buoyant non-spherical particles exhibit multi-rotation modes in viscoelastic–inertial shear flows. These peculiar orientational characteristics have not been found in the flow systems governed by a single effect. The present results could be potentially used to design the rheology-based control strategy for guiding particles to realize specific orientations in complex fluids.
4. Conclusions
In this work, we numerically investigate the rotational and orientational dynamics of a neutrally buoyant spheroid immersed in viscoelastic shear flow with finite fluid inertia. The fluid viscoelasticity is described by the Giesekus model. The interplay between particle and viscoelastic fluid is realized by the IBM. With weak fluid inertia (
$Re_p=0.1$), the influence of fluid rheology on the particle rotational dynamics in the shear plane is analysed in detail. For moderate fluid inertia (
$Re_p=10.0$), we focus on the modulations of the particle 3-D orbit for different fluid elasticities. The main conclusions are:
(i) With weak fluid inertia, the particle rotation rate is remarkably reduced by fluid elasticity. The particles with large eccentricity (
$AR = 4.0$) reach a non-rotational state in viscoelastic shear flow ($Wi = 2.0$). This observation reveals that, within the range of $Wi$ considered in the present study ($Wi = 0.0\sim 5.0$), fluid elasticity stabilizes the particle rotation in a viscoelastic fluid. Additionally, the fluid elasticity brings asymmetry into the particle rotation process where the particle deceleration takes a longer time than acceleration.(ii) The rotational dynamics of particles are affected by the solvent viscosity ratio and the mobility factor in different ways: the period of the particle rotation decreases monotonically with the solvent viscosity ratio. In contrast, the particle rotation period changes non-monotonically with the mobility factor. The results indicate that there exists a critical mobility factor for a viscoelastic fluid to minimize the reduction of the particle rotation rate in viscoelastic shear flows.
(iii) With moderate fluid inertia, when fluid elasticity is weak, the particle spirals toward the shear plane and eventually exhibits a tumbling mode, which is caused by the particle inertia. The fluid elasticity slows down the drift rate of the particle orbit. With increasing fluid elasticity, the competition among fluid elasticity, fluid inertia and particle inertia cause the particle to be attracted to a stable limit cycle between the shear plane and vorticity direction. This stable limit cycle results in a new particle rotation mode, i.e. asymmetric-kayaking mode.
(iv) The neutrally buoyant prolate particles exhibit multi-rotation modes in viscoelastic–inertial shear flows. Compared with the orientation behaviour of inertia-free particles in the Stokesian viscoelastic shear flows, four critical elastic numbers and one new orientation mode (asymmetric-kayaking mode) are observed in the present particle-laden viscoelastic flow system with finite fluid inertia.
In summary, the main contributions of the present work are: (i) comprehensively elaborating on the effects of rheological factors of viscoelastic fluid on the particle rotational dynamics; and (ii) a first attempt to give the overall picture of rotation modes induced by the elasto-inertial effect for a neutrally buoyant spheroid in viscoelastic shear flow at a finite Reynolds number. The results of the present work might enrich our understanding of the peculiar rotation and orientation dynamics of non-spherical particles in viscoelastic–inertial flows. Furthermore, from the applied perspective, the present results could also potentially be used to design a rheology-based controlling strategy for guiding particles to realize specific orientations in complex fluids.
Finally, it is worthwhile noting that the present computational framework of particle-laden viscoelastic flow is convenient to tackle the rotation of complex particles. A possible extension of the present research is to explore the elasto-inertial rotation of spheroids with a non-smooth or non-analytical closed surface, which may give additional insights into the dynamics of complex particles in viscoelastic fluids.
Funding
The authors are grateful for the support of the Natural Science Foundation of China through grant nos. 92252104 and 92252204.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Validation of numerical approach
The present study aims at investigating the rotation of particles in viscoelastic shear flows. Thus, we validate the numerical methods from two aspects: (i) particle rotation and (ii) fluid elastic effect.
A.1. Spheroid rotation in a Newtonian shear flow with zero fluid inertia
Jeffery orbit (Jeffery Reference Jeffery1922) is a canonical benchmark problem used to check the accuracy of a particle solver (Rosén et al. Reference Rosén, Lundell and Aidun2014, Reference Rosén, Do-Quang, Aidun and Lundell2015a). We used it here to validate the performance of the present particle solver when resolving the particle rotational dynamics. In this validation case, the particle aspect ratio is set as 
$AR = 2.0$, and the particle Reynolds number and Stokes number are consistent, i.e. 
$Re_p = St =0.1$. Thus, both the fluid and particle inertial effects are weak. The comparisons of numerical and theoretical results (Jeffery Reference Jeffery1922) are shown in figure 23, in which the calculated particle orientation and angular velocity agree well with the theoretical results. The comparison of results indicates that the present numerical method could accurately predict particle rotation in linear shear flow.
Figure 23. Comparisons of calculated results of a prolate spheroid (
$AR = 2.0$) with theoretical solutions of Jeffery (Reference Jeffery1922): (a) azimuthal angle; (b) angle velocity.
A.2. Spheroid rotation in a viscoelastic shear flow with zero fluid inertia
The particle rotation in the viscoelastic shear flow within the Stokesian regime is used to check the capability of the present method to capture the fluid elastic effect on particle rotation. In this test case, the particle Reynolds number is 
$Re_p = 0.1$. The Weissenberg number ranges from 0 to 4.0. We first validate the dependence of average angular velocity, 
$\bar {\omega }$, of particles with different aspect ratios on the Weissenberg number. The comparison of results is shown in figure 24, in which the calculated average angular velocity of particles is generally consistent with the reference results from D'Avino et al. (Reference D'Avino, Hulsen, Greco and Maffettone2014), although a little deviation exists when the fluid elastic effect becomes significant (
$Wi > 1.0$). Such little deviation might be caused by two reasons: (i) the momentum equation used is different, in the present study, the Navier–Stokes equation is utilized to resolve the flow field, while the Stokes equation is used in the reference; (ii) the solution method of the constitutive equation is different. In the present study, the constitutive equation is solved by the standard-conformation tensor formulation, whereas the log-representation formula is used by D'Avino et al. (Reference D'Avino, Hulsen, Greco and Maffettone2014) to stabilize the simulation of viscoelastic flow with strong fluid elasticity. There may be a little difference in resolving the viscoelastic fluid–solid interaction by these two methods under the highly elastic effect (Castillo & Codina Reference Castillo and Codina2015).
Figure 24. Comparisons of calculated average angular velocity of particle with the results from D'Avino et al. (Reference D'Avino, Hulsen, Greco and Maffettone2014).
From figure 24, we can see that the rotational dynamics of the particle with large eccentricity is more easily affected by fluid elasticity. Specifically, the particles with large aspect ratios (
$AR = 4.0$) can remain stationary in highly viscoelastic shear flow (
$Wi>1.5$). Overall, the comparison of results shows that the present numerical method could readily estimate the reduction of the particle rotation rate by fluid elasticity.
To further validate the performance of the present method for predicting the orientation of non-spherical particles in viscoelastic shear flows, we also contrast the particle orientation modes calculated with those from previous results (D'Avino et al. Reference D'Avino, Hulsen, Greco and Maffettone2014). Figure 25 illustrates the orientation modes of a prolate particle (
$AR=4.0$) under different fluid elasticities. From figure 25, it is found that the present method can capture the transitions of orientation modes of a prolate particle. There exist four different orientation modes in the present simulations: kayaking mode, orientation between the flow and vorticity direction, bi-stable orientation mode and flow-alignment mode. Different from the elasticity-induced orientation modes of inertia-free particles reported by D'Avino et al. (Reference D'Avino, Hulsen, Greco and Maffettone2014), the particle rotates as a ‘kayaking’ mode in the present simulation (figure 25a,e), rather than the ‘log-rolling’ mode in the weakly viscoelastic shear flows with zero inertial effect. However, the present ‘kayaking’ rotation mode is also found in the simulation by Wang et al. (Reference Wang, Yu and Lin2019).
Figure 25. Orientation modes of a neutrally prolate particle (
$AR = 4.0$) in viscoelastic shear flows with different elasticities. (a) 
$Wi = 1.0$, (b) 
$Wi = 2.7$, (c) 
$Wi = 3.0$, (d) 
$Wi = 4.5$, (e) 
$Wi = 1.0$, (f) 
$Wi = 2.7$, (g) 
$Wi = 3.0$, (h) 
$Wi = 4.5$.
The final rotational state of particles could reveal the dominant effect in the particle-laden flow system. If the final rotation mode is a time-periodic mode for particle and fluid flow, the dominant effect generally is particle inertia (Rosén et al. Reference Rosén, Lundell and Aidun2014). From this point, the particle inertia might result in the present kayaking mode in figures 25(a) and 25(e). Considering this, we additionally perform another case, where the particle density is less than that of the fluid, i.e. density ratio 
$\rho _r=0.5$, to validate the effect of particle inertia on the present kayaking mode.
Figure 26 shows that, when decreasing particle inertia, the lighter particles with different initial orientations all spirally approach the vorticity direction, and finally behave in the ‘log-rolling’ mode as reported by D'Avino et al. (Reference D'Avino, Hulsen, Greco and Maffettone2014) for an inertia-free particle in weakly viscoelastic shear flows. Therefore, we might conclude that the present ‘kayaking’ mode might be due to particle inertia. Furthermore, the above test results indicate that the competition among fluid inertia (
$Re_p$), particle inertia (
$St$) and fluid elasticity (
$Wi$) can lead to the peculiar particle rotation behaviours which could not be observed in the previous studies governed by a single effect. This motivates the present research in § 3.
Figure 26. Effect of particle inertia on the orientation modes of a prolate particle (
$AR = 4.0$) in viscoelastic shear flow with 
$Wi = 1.0$, 
$Re_p = 0.1$: panels (a i,b i) show the 3-D trajectory of the tip of particle with the different initial orientation 
$(\phi,\theta,\psi )_0 =(0.5{\rm \pi}, 0.4{\rm \pi}, 0)$ and 
$(0.5{\rm \pi}, 0.1{\rm \pi}, 0)$, respectively; (a ii,b ii) show the coordinates of the particle tip; (a iii,b iii) show the particle trajectory projected on the 
$x$–
$y$ plane; (a iv,b iv) show the particle angular velocities in the particle frame.
A.3. Spheroid rotation in a Newtonian shear flow with fluid inertia
The present study focuses on the effect of fluid inertia on the rotational dynamics of spheroids in viscoelastic flows. Thus, we first examine the capability of the present numerical approach to capture the effect of fluid inertia on particle rotation in a Newtonian shear flow. In this test case, a spheroid with different aspect ratios (
$AR=2.0$ and 
$0.5$) is immersed in a Newtonian shear flow at 
$Re_p=5.0$, 
$12.8$ and 
$64.0$. The simulation parameters are consistent with those in earlier studies (Ding & Aidun Reference Ding and Aidun2000; Yu et al. Reference Yu, Phan-Thien and Tanner2007). The comparison of results is shown in figure 27, where the present spheroid rotation rate (
${\rm d}\phi /{\rm d}t$) at different azimuthal angles (
$\phi$) agrees well with that reported by Yu et al. (Reference Yu, Phan-Thien and Tanner2007), as shown in figures 27(a) and 27(b). The angular velocity of the spheroid with 
$AR=0.5$ is also in good agreement with that from Ding & Aidun (Reference Ding and Aidun2000), as shown in figure 27(c). The comparison of results shows that the present numerical approach can capture the effect of fluid inertia on the spheroid rotation.
Figure 27. Comparison of calculated spheroid rotation rate with the reference results (Ding & Aidun Reference Ding and Aidun2000; Yu et al. Reference Yu, Phan-Thien and Tanner2007) in Newtonian shear flow with 
$AR=2.0$ (a,b) and 
$AR=0.5$ (c).
A.4. Sphere rotation in a sheared viscoelastic flow resolved within Navier-Stokes framework
To explore the coupled effect of fluid elasticity and fluid inertia on particle rotation, we further verify the present numerical approach by computing the rotation of a single sphere immersed in a viscoelastic shear flow. The validation results are shown in figure 28, where the present angular velocity of the sphere agrees well with experiments (Snijkers et al. Reference Snijkers, D'Avino, Maffettone, Greco, Hulsen and Vermant2009) and with the numerical results obtained within the Navier–Stokes framework (Krishnan et al. Reference Krishnan, Shaqfeh and Iaccarino2017). This validation indicates that the present numerical methods within the Navier–Stokes framework are reliable in resolving the coupled effect of fluid elasticity and fluid inertia on particle rotation.
Figure 28. Comparison of calculated spheroid rotation rate with the experiments (Snijkers et al. Reference Snijkers, D'Avino, Maffettone, Greco, Hulsen and Vermant2009) and simulation results (Snijkers et al. Reference Snijkers, D'Avino, Maffettone, Greco, Hulsen and Vermant2011; Krishnan, Shaqfeh & Iaccarino Reference Krishnan, Shaqfeh and Iaccarino2017).
Moreover, the accuracy of the present numerical solver is systematically validated by several canonical benchmark examples of viscoelastic fluid flows in our recent study (Li et al. Reference Li, Huang, Xu and Zhao2022).
In summary, the accuracy and capability of the present numerical approach are verified by four benchmark examples of particle rotation in Newtonian and viscoelastic shear flows. All validation results reveal that the present methods can accurately simulate the particle dynamics in viscoelastic shear flows.
A.5. Grid resolution effect
To check the effect of grid resolution on the particle rotation, we simulated the rotation of a prolate particle (
$AR = 2.0$) in a viscoelastic shear flow on three meshes with different spatial resolutions; the results are shown in figure 29. The angular velocities at different orientations calculated on different meshes agree well with each other (figure 29a). This agreement indicates that the present grid resolution (
$\varDelta = 1/32D_p$) is capable of giving the grid-independence solution of particle angular velocity at different orientations.
Figure 29. Effect of grid resolution on the particle rotation: (a) angular velocity vs particle orientation in the polar coordinate system, 
$AR = 2.0$,
$Re_p = 0.1$, 
$Wi=2.0$; (b) orientation modes of a prolate spheroid with 
$AR = 4.0$,
$Re_p = 10.0$, 
$Wi=5.0$.
To further evaluate the grid resolution effect on the 3-D orientation mode of the particle, we also calculated the 3-D trajectory of the particle tip (
$AR = 4.0$) in viscoelastic shear flow with finite fluid inertia (
$Re_p = 10.0$, 
$Wi=5.0$). Figure 29(b) shows that the equilibrium orientation modes of the particle are not changed with increasing grid resolution. Note that a small domain size of 
$L \times H \times W = 2 \times 2 \times 2$ is chosen in this test case to save the computational cost.
Moreover, in earlier studies on the single effect (fluid inertia or fluid elasticity), the grid resolutions used for calculating the rotation of the spheroid are approximately 
$\varDelta = 1/32D_p$ for prolate spheroids in a Newtonian shear flow (Yu et al. Reference Yu, Phan-Thien and Tanner2007) and 
$\varDelta = 1/16 \sim 1/42D_p$ for spheroids (
$AR = 1.0$ and 
$4.0$) in a viscoelastic shear flow (Krishnan et al. Reference Krishnan, Shaqfeh and Iaccarino2017; Wang et al. Reference Wang, Yu and Lin2019; Rosti & Brandt Reference Rosti and Brandt2020). Therefore, both the present convergence test and the previous studies indicate that the particle rotation modes obtained using the mesh with the present mesh resolution (
$\varDelta = 1/32D_p$) are reliable.
