Hostname: page-component-77c89778f8-m8s7h Total loading time: 0 Render date: 2024-07-17T03:11:37.404Z Has data issue: false hasContentIssue false
  • English
  • Français

Lubricating motion of a sphere towards a thin porous slab with Saffman slip condition

Published online by Cambridge University Press:  28 March 2019

Sondes Khabthani ,
Antoine Sellier Open the ORCID record for Antoine Sellier [Opens in a new window]  and
François Feuillebois
Sondes Khabthani
Affiliation:
Laboratoire Ingénierie Mathématique, École Polytechnique de Tunisie, rue El Khawarezmi, BP 743, La Marsa, Tunisia
Antoine Sellier*
Affiliation:
LadHyX, École Polytechnique, 91128 Palaiseau CEDEX, France
François Feuillebois
Affiliation:
LIMSI-CNRS, UPR 3251, BP 133, 91403 Orsay CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Near-contact hydrodynamic interactions between a solid sphere and a plane porous slab are investigated in the framework of lubrication theory. The size of pores in the slab is small compared with the slab thickness so that the Darcy law holds there. The slab is thin: that is, its thickness is small compared with the sphere radius. The considered problem involves a sphere translating above the slab together with a permeation flow across the slab and a uniform pressure below. The pressure is continuous across both slab interfaces and the Saffman slip condition applies on its upper interface. An extended Reynolds-like equation is derived for the pressure in the gap between the sphere and the slab. This equation is solved numerically and the drag force on the sphere is calculated therefrom for a wide range of values of the slab interface slip length and of the permeability parameter 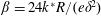$\unicode[STIX]{x1D6FD}=24k^{\ast }R/(e\unicode[STIX]{x1D6FF}^{2})$, where 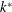$k^{\ast }$ is the permeability, $e$ is the porous slab thickness, 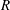$R$ is the sphere radius and 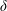$\unicode[STIX]{x1D6FF}$ is the gap. Moreover, asymptotics expansions for the pressure and drag are derived for high and low 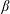$\unicode[STIX]{x1D6FD}$. These expansions, which agree with the numerics, are also handy formulae for practical use. All results match with those of other authors in particular cases. The settling trajectory of a sphere towards a porous slab in a fluid at rest is calculated from these results and, as expected, the time for reaching the slab decays for increasing slab permeability and upper interface slip length.

JFM classification

Low-Reynolds-number flows: Lubrication theory Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 949 - 968
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions. Dover Publications.Google Scholar
Bazant, M. & Vinagradova, O. I. 2008 Tensorial hydrodynamic slip. J. Fluid Mech. 613, 125–134.Google Scholar
Beavers, G. & Joseph, D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207.Google Scholar
Brinkman, H. 1947 A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A 1, 27–34.Google Scholar
Carotenuto, C. & Minale, M. 2011 Shear flow over a porous layer: velocity in the real proximity of the interface via rheological tests. Phys. Fluids 23 (6), 063101.Google Scholar
Darcy, H. 1856 Les Fontaines Publiques de la Ville de Dijon. Dalmont.Google Scholar
Davis, A. M. J., Kezirian, M. T. & Brenner, H. 1994 On the Stokes–Einstein model of surface diffusion along solid surfaces: slip boundary conditions. J. Colloid Interface Sci. 1065, 129–140.Google Scholar
Debbech, A., Elasmi, L. & Feuillebois, F. 2010 The method of fundamental solution for the creeping flow around a sphere close to a membrane. Z. Angew. Math. Mech. 90 (12), 920–928.Google Scholar
Elasmi, L. & Feuillebois, F. 2001 Green function for a Stokes flow near a porous slab. Z. Angew. Math. Mech. 81 (11), 743–752.Google Scholar
Elasmi, L. & Feuillebois, F. 2003 Integral equation method for creeping flow around a solid body near a porous slab. Q. J. Mech. Appl. Math. 56 (2), 163–185.Google Scholar
Ghalia, N., Feuillebois, F. & Sellier, A. 2016 A sphere in a second degree polynomial creeping flow parallel to a plane, impermeable and slipping wall. Q. J. Mech. Appl. Maths 69, 353–390.Google Scholar
Goren, S. L. 1973 The hydrodynamic force resisting the approach of a sphere to a plane wall in slip flow. J. Colloid Interface Sci. 44 (2), 356–360.Google Scholar
Goren, S. L. 1979 The hydrodynamic force resisting the approach of a sphere to a plane permeable wall. J. Colloid Interface Sci. 69 (1), 78–85.Google Scholar
Handy, W. B. & Bircumshaw, I. 1925 Bakerian lecture. Boundary lubrication – plane surfaces and the limitations of Amontons’ law. Proc. R. Soc. Lond. A 108 (745), 1–27.Google Scholar
Hocking, L. M. 1973 The effect of slip on the motion of a sphere close to a wall and of two adjacent spheres. J. Engng Maths 7 (3), 207–221.Google Scholar
Karmakar, T. & Raja Sekhar, G. P. 2018 Squeeze-film flow between a flat impermeable bearing and an anisotropic porous bed. Phys. Fluids 30, 043604.Google Scholar
Le-Clech, P., Chen, V. & Fane, T. A. G. 2006 Fouling in membrane bioreactors used in wastewater treatment. J. Membr. Sci. 284, 17–53.Google Scholar
Lecoq, N., Anthore, R., Cichocki, B., Szymczak, P. & Feuillebois, F. 2004 Drag force on a sphere moving towards a corrugated wall. J. Fluid Mech. 513, 247–264.Google Scholar
Lin, J.-R., Lu, R.-F. & Yang, C.-B. 2001 Derivation of porous squeeze-film Reynolds equations using the Brinkman model and its application. J. Phys. D Appl. Phys. 34, 3217–3223.Google Scholar
Loussaief, H., Pasol, L. & Feuillebois, F. 2015 Motion of a spherical particle in a viscous fluid along a slip wall. Q. J. Mech. Appl. Maths 68 (2), 115–144.Google Scholar
Luo, H. & Pozrikidis, C. 2008 Effect of surface slip on Stokes flow past a spherical particle in infinite fluid and near a plane wall. J. Engng Maths 62, 1–21.Google Scholar
Michalopoulou, A. C., Burganos, V. N. & Payatakes, A. C. 1992 Creeping axisymmetric flow around a solid particle near a permeable obstacle. AIChE J. 38 (8), 1213–1228.Google Scholar
Navier, C. L. M. H. 1823 Mémoire sur les lois du mouvement des fluides. Mémoires de l’Acad. des Sciences de l’Institut de France 6, 389–416.Google Scholar
Nguyen, A. V. 2000 Historical note on the Stefan–Reynolds equations. J. Colloid Interface Sci. 231 (1), 195.Google Scholar
Nield, D. A. & Bejan, A. 2006 Convection in Porous Media. Springer.Google Scholar
Nir, A. 1981 On the departure of a sphere from contact with a permeable membrane. J. Engng Maths 15 (1), 65–75.Google Scholar
Ochoa-Tapia, J. A. & Whitaker, S. 1995a Momentum transfer at the boundary between a porous medium and a homogeneous fluid. I. Theoretical development. Intl J. Heat Mass Transfer 38 (14), 2635–2646.Google Scholar
Ochoa-Tapia, J. A. & Whitaker, S. 1995b Momentum transfer at the boundary between a porous medium and a homogeneous fluid. II. Comparison with experiment. Intl J. Heat Mass Transfer 38 (14), 2647–2655.Google Scholar
Ramon, G. Z., Huppert, H. E., Lister, J. R. & Stone, H. A. 2013 On the hydrodynamic interaction between a particle and a permeable surface. Phys. Fluids. 25, 073103.Google Scholar
Reynolds, O. 1886 IV. On the theory of lubrication and its application to Mr. Beauchamp Tower’s experiments, including an experimental determination of the viscosity of olive oil. Phil. Trans. R. Soc. Lond. 177, 157–234.Google Scholar
Saffman, P. G. 1971 On the boundary condition at the surface of a porous medium. Stud. Appl. Maths 1 (2), 93–101.Google Scholar
Sherwood, J. D. 1988 The force on a sphere pulled away from a permeable half-space. Physico-Chem. Hydrodyn. 10 (1), 3–12.Google Scholar
Vinogradova, O. I. 1995 Drainage of a thin liquid film confined between hydrophobic surfaces. Langmuir 11, 2213–2220.Google Scholar
Wu, Z. & Mirbod, P. 2018 Experimental analysis of the flow near the boundary of random porous media. Phys. Fluids 30 (4), 047103.Google Scholar