Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T12:48:55.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat transfer in rapidly rotating convection with heterogeneous thermal boundary conditions

Published online by Cambridge University Press:  05 September 2017

Jon E. Mound Open the ORCID record for Jon E. Mound [Opens in a new window]  and
Christopher J. Davies
Jon E. Mound*
Affiliation:
School of Earth and Environment, University of Leeds, Leeds LS2 9JT, UK
Christopher J. Davies
Affiliation:
School of Earth and Environment, University of Leeds, Leeds LS2 9JT, UK Institute of Geophysics and Planetary Physics, Scripps Institution of Oceanography, University of California at San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0225, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Convection in the metallic cores of terrestrial planets is likely to be subjected to lateral variations in heat flux through the outer boundary imposed by creeping flow in the overlying silicate mantles. Boundary anomalies can significantly influence global diagnostics of core convection when the Rayleigh number, 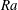$Ra$, is weakly supercritical; however, little is known about the strongly supercritical regime appropriate for planets. We perform numerical simulations of rapidly rotating convection in a spherical shell geometry and impose two patterns of boundary heat flow heterogeneity: a hemispherical 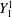$Y_{1}^{1}$ spherical harmonic pattern; and one derived from seismic tomography of the Earth’s lower mantle. We consider Ekman numbers 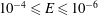$10^{-4}\leqslant E\leqslant 10^{-6}$, flux-based Rayleigh numbers up to 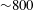${\sim}800$ times critical, and a Prandtl number of unity. The amplitude of the lateral variation in heat flux is characterised by 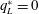$q_{L}^{\ast }=0$, 2.3, 5.0, the peak-to-peak amplitude of the outer boundary heat flux divided by its mean. We find that the Nusselt number, 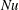$Nu$, can be increased by up to ${\sim}25\,\%$ relative to the equivalent homogeneous case due to boundary-induced correlations between the radial velocity and temperature anomalies near the top of the shell. The 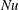$Nu$ enhancement tends to become greater as the amplitude and length scale of the boundary heterogeneity are increased and as the system becomes more supercritical. This 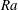$Ra$ dependence can steepen the 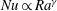$Nu\propto Ra^{\unicode[STIX]{x1D6FE}}$ scaling in the rotationally dominated regime, with 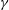$\unicode[STIX]{x1D6FE}$ for our most extreme case approximately 20 % greater than the equivalent homogeneous scaling. Therefore, it may be important to consider boundary heterogeneity when extrapolating numerical results to planetary conditions.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 601 - 629
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Alboussière, T., Deguen, R. & Melzani, M. 2010 Melting-induced stratification above the Earth’s inner core due to convective translation. Nature 466 (7307), 744–747.CrossRefGoogle ScholarPubMed
Amit, H., Aubert, J. & Hulot, G. 2010 Stationary, oscillating or drifting mantle-driven geomagnetic flux patches? J. Geophys. Res. 115 (B7), B07108.Google Scholar
Amit, H., Choblet, G., Olson, P., Monteux, J., Deschamps, F., Langlais, B. & Tobie, G. 2015a Towards more realistic core–mantle boundary heat flux patterns: a source of diversity in planetary dynamos. Prog. Earth Planetary Sci. 2, 26.CrossRefGoogle Scholar
Amit, H., Deschamps, F. & Choblet, G. 2015b Numerical dynamos with outer boundary heat flux inferred from probabilistic tomography – consequences for latitudinal distribution of magnetic flux. Geophys. J. Intl 203, 840–855.CrossRefGoogle Scholar
Aurnou, J. M., Calkins, M. A., Cheng, J. S., Julien, K., King, E. M., Nieves, D., Soderlund, K. M. & Stellmach, S. 2015 Rotating convective turbulence in Earth and planetary cores. Phys. Earth Planet. Inter. 246, 52–71.CrossRefGoogle Scholar
Bloxham, J. 2000 The effect of thermal core–mantle interactions on the palaeomagnetic secular variation. Phil. Trans. R. Soc. Lond. A 358 (1768), 1171–1179.CrossRefGoogle Scholar
Busse, F. H. 2002 Convective flows in rapidly rotating spheres and their dynamo action. Phys. Fluids 14 (4), 1301–1314.CrossRefGoogle Scholar
Calkins, M. A., Hale, K., Julien, K., Nieves, D., Driggs, D. & Marti, P. 2015 The asymptotic equivalence of fixed heat flux and fixed temperature thermal boundary conditions for rapidly rotating convection. J. Fluid Mech. 784, R2.CrossRefGoogle Scholar
Cheng, J. S., Stellmach, S., Ribeiro, A., Grannan, A., King, E. M. & Aurnou, J. M. 2015 Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Intl 201, 1–17.CrossRefGoogle Scholar
Childs, H., Brugger, E., Whitlock, B., Meredith, J., Ahern, S., Pugmire, D., Biagas, K., Miller, M., Harrison, C., Weber, G. H. et al. 2012 VisIt: an end-user tool for visualizing and analyzing very large data. In High Performance Visualization (ed. Wes Bethel, E., Childs, H. & Hansen, C.), pp. 357–372. Chapman and Hall.Google Scholar
Davies, C. J. 2015 Cooling history of Earth’s core with high thermal conductivity. Phys. Earth Planet. Inter. 247, 65–79.CrossRefGoogle Scholar
Davies, C. J., Gubbins, D. & Jimack, P. K. 2009 Convection in a rapidly rotating spherical shell with an imposed laterally varying thermal boundary condition. J. Fluid Mech. 641, 335–358.CrossRefGoogle Scholar
Davies, C. J., Gubbins, D., Willis, A. P. & Jimack, P. K. 2008 Time-averaged paleomagnetic field and secular variation: predictions from dynamo solutions based on lower mantle seismic tomography. Phys. Earth Planet. Inter. 169 (1–4), 194–203.CrossRefGoogle Scholar
Dietrich, W., Hori, K. & Wicht, J. 2016 Core flows and heat transfer induced by inhomogeneous cooling with sub- and supercritical convection. Phys. Earth Planet. Inter. 251, 36–51.CrossRefGoogle Scholar
Garnero, E. J., McNamara, A. K. & Shim, S.-H. 2016 Continent-sized anomalous zones with low seismic velocity at the base of Earth’s mantle. Nat. Geosci. 9 (7), 481–489.CrossRefGoogle Scholar
Gastine, T., Wicht, J. & Aubert, J. 2016 Scaling regimes in spherical shell rotating convection. J. Fluid Mech. 808, 690–732.CrossRefGoogle Scholar
Gastine, T., Wicht, J. & Aurnou, J. M. 2015 Turbulent Rayleigh–Bénard convection in spherical shells. J. Fluid Mech. 778, 721–764.CrossRefGoogle Scholar
Gelman, S. E., Elkins-Tanton, L. T. & Seager, S. 2011 Effects of stellar flux on tidally locked terrestrial planets: degree-1 mantle convection and local magma ponds. Astrophys. J. 735 (2), 72.CrossRefGoogle Scholar
Gibbons, S. J., Gubbins, D. & Zhang, K. 2007 Convection in rotating spherical fluid shells with inhomogeneous heat flux at the outer boundary. Geophys. Astrophys. Fluid Dyn. 101 (5–6), 347–370.CrossRefGoogle Scholar
Gillet, N. & Jones, C. A. 2006 The quasi-geostrophic model for rapidly rotating spherical convection outside the tangent cylinder. J. Fluid Mech. 554, 343–369.CrossRefGoogle Scholar
Gilman, P. A. 1977 Nonlinear dynamics of Boussinesq convection in a deep rotating spherical shell-i. Geophys. Astrophys. Fluid Dyn. 8 (1), 93–135.CrossRefGoogle Scholar
Goluskin, D. 2015 Internally Heated Convection and Rayleigh–Bénard Convection. Springer.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86 (15), 3316–3319.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66 (1), 016305.Google ScholarPubMed
Gubbins, D., Willis, A. P. & Sreenivasan, B. 2007 Correlation of Earth’s magnetic field with lower mantle thermal and seismic structure. Phys. Earth Planet. Inter. 162 (3–4), 256–260.CrossRefGoogle Scholar
Helffrich, G. & Kaneshima, S. 2013 Causes and consequences of outer core stratification. Phys. Earth Planet. Inter. 223 (C), 2–7.CrossRefGoogle Scholar
Hunter, J. D. 2007 Matplotlib: a 2D graphics environment. Comput. Sci. Engng 9 (3), 90–95.CrossRefGoogle Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102 (6), 064501.CrossRefGoogle ScholarPubMed
Jones, C. A. 2015 Thermal and compositional convection in the outer core. In Treatise on Geophysics, 2nd edn (ed. Schubert, G.), vol. 8, pp. 115–159. Elsevier.CrossRefGoogle Scholar
Julien, K., Aurnou, J. M., Calkins, M. A., Knobloch, E., Marti, P., Stellmach, S. & Vasil, G. M. 2016 A nonlinear model for rotationally constrained convection with Ekman pumping. J. Fluid Mech. 798, 50–87.CrossRefGoogle Scholar
Julien, K., Knobloch, E., Rubio, A. M. & Vasil, G. M. 2012a Heat transport in low-Rossby-number Rayleigh–Bénard convection. Phys. Rev. Lett. 109 (25), 254503.CrossRefGoogle ScholarPubMed
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012b Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106 (4–5), 392–428.CrossRefGoogle Scholar
Kavner, A. & Rainey, E. S. G. 2016 Heat transfer in the core and mantle. In Deep Earth Physics and Chemistry of the Lower Mantle and Core, Geophysical Monograph Series (ed. Terasaki, H. & Fischer, R. A.), pp. 31–42. Wiley.CrossRefGoogle Scholar
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.CrossRefGoogle Scholar
King, E. M., Stellmach, S. & Buffett, B. 2013 Scaling behaviour in Rayleigh–Bénard convection with and without rotation. J. Fluid Mech. 717, 449–471.CrossRefGoogle Scholar
King, E. M., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. M. 2009 Boundary layer control of rotating convection systems. Nature 457 (7227), 301–304.CrossRefGoogle ScholarPubMed
Kono, M. 2015 Geomagnetism: an introduction and overview. In Treatise on Geophysics, 2nd edn (ed. Schubert, G.), vol. 5, pp. 1–31. Elsevier.Google Scholar
Lay, T., Hernlund, J. & Buffett, B. A. 2008 Core–mantle boundary heat flow. Nat. Geosci. 1 (1), 25–32.CrossRefGoogle Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225 (1161), 196–212.Google Scholar
Masters, G., Johnson, S., Laske, G. & Bolton, H. 1996 A shear-velocity model of the mantle. Phil. Trans. R. Soc. Lond. A 354 (1711), 1385–1411.Google Scholar
Matsui, H., Heien, E., Aubert, J., Aurnou, J. M., Avery, M., Brown, B., Buffett, B. A., Busse, F., Christensen, U. R., Davies, C. J. et al. 2016 Performance benchmarks for a next generation numerical dynamo model. Geochem. Geophys. Geosyst. 17 (5), 1586–1607.CrossRefGoogle Scholar
Nakagawa, T. & Tackley, P. J. 2008 Lateral variations in CMB heat flux and deep mantle seismic velocity caused by a thermal–chemical-phase boundary layer in 3D spherical convection. Earth Planet. Sci. Lett. 271 (1–4), 348–358.CrossRefGoogle Scholar
Nimmo, F. 2015 Thermal and compositional evolution of the core. In Treatise on Geophysics, 2nd edn (ed. Schubert, G.), vol. 9, pp. 201–219. Elsevier.CrossRefGoogle Scholar
Oliveira, J. S. & Wieczorek, M. A. 2017 Testing the axial dipole hypothesis for the Moon by modeling the direction of crustal magnetization. J. Geophys. Res. 122 (2), 383–399.CrossRefGoogle Scholar
Olson, P. 2003 Thermal interaction of the core and mantle. In Earth’s Core and Lower Mantle, pp. 1–38. Taylor & Francis.Google Scholar
Olson, P. 2016 Mantle control of the geodynamo: consequences of top–down regulation. Geochem. Geophys. Geosyst. 17 (5), 1935–1956.CrossRefGoogle Scholar
Olson, P. & Christensen, U. R. 2002 The time-averaged magnetic field in numerical dynamos with non-uniform boundary heat flow. Geophys. J. Intl 151 (3), 809–823.CrossRefGoogle Scholar
Olson, P., Deguen, R., Hinnov, L. A. & Zhong, S. 2013 Controls on geomagnetic reversals and core evolution by mantle convection in the Phanerozoic. Phys. Earth Planet. Inter. 214 (C), 87–103.CrossRefGoogle Scholar
Olson, P., Deguen, R., Rudolph, M. L. & Zhong, S. 2015 Core evolution driven by mantle global circulation. Phys. Earth Planet. Inter. 243 (C), 44–55.CrossRefGoogle Scholar
Orszag, S. A. 1971 Numerical simulation of incompressible flows within simple boundaries. I. Galerkin (spectral) representations. Stud. Appl. Maths 50 (4), 293–327.CrossRefGoogle Scholar
Otero, J., Wittenberg, R. W., Worthing, R. A. & Doering, C. R. 2002 Bounds on Rayleigh–Bénard convection with an imposed heat flux. J. Fluid Mech. 473, 191–199.CrossRefGoogle Scholar
Plumley, M., Julien, K., Marti, P. & Stellmach, S. 2016 The effects of Ekman pumping on quasi-geostrophic Rayleigh–Bénard convection. J. Fluid Mech. 803, 51–71.CrossRefGoogle Scholar
Spiegel, E. A. & Veronis, G. 1960 On the Boussinesq approximation for a compressible fluid. Astrophys. J. 131, 442–447.CrossRefGoogle Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
Šrámek, O. & Zhong, S. 2010 Long-wavelength stagnant lid convection with hemispheric variation in lithospheric thickness: link between Martian crustal dichotomy and Tharsis? J. Geophys. Res. 115 (E9), E09010.Google Scholar
Stellmach, S., Lischper, M., Julien, K., Vasil, G., Cheng, J. S., Ribeiro, A., King, E. M. & Aurnou, J. M. 2014 Approaching the asymptotic regime of rapidly rotating convection: boundary layers versus interior dynamics. Phys. Rev. Lett. 113 (25), 254501.CrossRefGoogle ScholarPubMed
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.CrossRefGoogle Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
Sumita, I. & Olson, P. 1999 A laboratory model for convection in Earth’s core driven by a thermally heterogeneous mantle. Science 286 (5444), 1547–1549.CrossRefGoogle ScholarPubMed
Sumita, I. & Olson, P. 2002 Rotating thermal convection experiments in a hemispherical shell with heterogeneous boundary heat flux: implications for the Earth’s core. J. Geophys. Res. 107 (B8), 2169.Google Scholar
Takahashi, F. & Tsunakawa, H. 2009 Thermal core–mantle coupling in an early lunar dynamo: implications for a global magnetic field and magnetosphere of the early Moon. Geophys. Res. Lett. 36 (24), L24202.CrossRefGoogle Scholar
Willis, A. P., Sreenivasan, B. & Gubbins, D. 2007 Thermal core–mantle interaction: exploring regimes for ‘locked’ dynamo action. Phys. Earth Planet. Inter. 165 (1–2), 83–92.CrossRefGoogle Scholar
Zhang, K. & Gubbins, D. 1993 Convection in a rotating spherical fluid shell with an inhomogeneous temperature boundary condition at infinite Prandtl number. J. Fluid Mech. 250, 209–232.CrossRefGoogle Scholar
Zhang, K. & Gubbins, D. 1996 Convection in a rotating spherical fluid shell with an inhomogeneous temperature boundary condition at finite Prandtl number. Phys. Fluids 8 (5), 1141–1148.CrossRefGoogle Scholar
Zhang, N. & Zhong, S. 2011 Heat fluxes at the Earth’s surface and core–mantle boundary since Pangea formation and their implications for the geomagnetic superchrons. Earth Planet. Sci. Lett. 306 (3–4), 205–216.CrossRefGoogle Scholar
Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102 (4), 044502.Google ScholarPubMed
Zhong, S. 2009 Migration of Tharsis volcanism on Mars caused by differential rotation of the lithosphere. Nat. Geosci. 2 (1), 19–23.CrossRefGoogle Scholar
Zhong, S., Zhang, N., Li, Z.-X. & Roberts, J. H. 2007 Supercontinent cycles, true polar wander, and very long-wavelength mantle convection. Earth Planet. Sci. Lett. 261 (3–4), 551–564.CrossRefGoogle Scholar