Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T12:54:49.595Z Has data issue: false hasContentIssue false
  • English
  • Français

Harmonic generation by nonlinear self-interaction of a single internal wave mode

Published online by Cambridge University Press:  05 September 2017

Scott Wunsch Open the ORCID record for Scott Wunsch [Opens in a new window]
Scott Wunsch*
Affiliation:
The Johns Hopkins University Applied Physics Laboratory, Laurel, MD 20723, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Weakly nonlinear theory is used to explore the dynamics of a single-mode internal tide in variable stratification with rotation. Nonlinear self-interaction in variable stratification generates a perturbation which is forced with double the original frequency and wavenumber. The dynamics of the perturbation is analogous to a forced harmonic oscillator, with the steady-state solution corresponding to a bound harmonic matching the forcing frequency and wavenumber. When the forcing frequency is near a natural frequency of the system, even a small-amplitude (nearly linear) internal tide may induce a significant harmonic response. 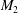Idealized stratification profiles are utilized to explore the relevance of this effect for oceanic $M_{2}$ baroclinic internal tides, and the results indicate that a rapidly growing harmonic may occur in some environments near the Equator, but is unlikely at higher latitudes. The results are relevant to recent observations of 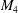$M_{4}$ (harmonic) internal tides in the South China Sea and elsewhere. More generally, nonlinear self-interaction may contribute to the transfer of energy to smaller scales and the dissipation of baroclinic internal tides, especially in equatorial waters.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Ocean processes Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 630 - 647
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J. & Peacock, T. 2009 Tidal conversion by supercritical topography. J. Phys. Oceanogr. 39, 1965–1974.Google Scholar
Bourget, B., Dauxois, T., Joubaud, S. & Odier, P. 2013 Experimental study of parametric subharmonic instability for plane internal waves. J. Fluid Mech. 723, 1–20.Google Scholar
Diamessis, P. J., Wunsch, S., Delwiche, I. & Richter, M. P. 2014 Nonlinear generation of harmonics through interaction of an internal wave beam with a model ocean pycnocline. Dyn. Atmos. Oceans 66, 110–137.Google Scholar
Dossmann, Y., Auclair, F. & Paci, A. 2013 Topographically induced internal solitary waves in a pycnocline: secondary generation and selection criteria. Phys. Fluids 25, 086603.Google Scholar
Garrett, C. 2003 Internal tides and ocean mixing. Science 308, 1858–1859.CrossRefGoogle Scholar
Garrett, C. & Kunze, E. 2007 Internal tide generation in the deep ocean. Annu. Rev. Fluid Mech. 39, 57–87.Google Scholar
Garrett, C. & Munk, W. 1979 Internal waves in the ocean. Annu. Rev. Fluid Mech. 11, 339–369.Google Scholar
Gayen, B. & Sarkar, S. 2013 Degradation of an internal wave beam by parametric subharmonic instability in an upper ocean pycnocline. J. Geophys. Res. Oceans 118, 4689–4698.CrossRefGoogle Scholar
Grisouard, N. & Staquet, C. 2010 Numerical simulations of the local generation of internal solitary waves in the bay of biscay. Nonlinear Process. Geophys. 17, 575–584.Google Scholar
Grisouard, N., Staquet, C. & Gerkema, T. 2011 Generation of internal solitary waves in a pycnocline by an internal wave beam: a numerical study. J. Fluid Mech. 676, 491–513.Google Scholar
Holloway, G. 1980 Oceanic internal waves are not weak waves. J. Phys. Oceanogr. 10, 906–914.Google Scholar
Johnston, T. M. S. & Merryfield, M. A. 2003 Internal tide scattering at seamounts, ridges, and islands. J. Geophys. Res. 108, 3180.Google Scholar
Kunze, E. & Llewellyn-Smith, S. G. 2004 The role of small-scale topography in the turbulent mixing of the global ocean. Oceanography 17, 55–64.Google Scholar
Lamb, K. 2004 Nonlinear interaction among internal wave beams generated by tidal flow over supercritical topography. Geophys. Res. Lett. 31, L09313.CrossRefGoogle Scholar
LeBlond, P. H. & Mysak, L. A. 1981 Waves in the Ocean. Elsevier.Google Scholar
MacKinnon, J. A. & Winters, K. B. 2005 Subtropical catastrophe: significant loss of low-mode tidal energy at 28.9 degrees. Geophys. Res. Lett. 32, L15605.Google Scholar
Mathur, M. & Peacock, T. 2009 Internal wave propagation in non-uniform stratifications. J. Fluid Mech. 639, 133–152.Google Scholar
McHugh, J. 2009 Internal waves at an interface between two layers of differing stability. J. Atmos. Sci. 28, 1845–1855.Google Scholar
Melet, A., Hallberg, R., Legg, S. & Polzin, K. 2013 Sensitivity of the ocean state to teh vertical distribution of internal-tide-driven mixing. J. Phys. Oceanogr. 43, 602–615.Google Scholar
Mercier, M. J., Mathur, M., Gostiaux, L., Gerkema, T., Magalhaes, J. M., da Silva, J. C. B. & Dauxois, T. 2012 Soliton generation by internal tidal beams impinging on a pycnocline: laboratory experiments. J. Fluid Mech. 704, 37–60.Google Scholar
Munk, W. & Wunsch, C. 1998 Abyssal recipes ii: energetics of tidal and wind mixing. Deep-Sea Res. I 45, 1977–2020.CrossRefGoogle Scholar
Peacock, T. & Tabaei, A. 2005 Visualization of nonlinear effects in reflecting internal wave beams. Phys. Fluids 17, 061702.CrossRefGoogle Scholar
Rainville, L. & Pinkel, R. 2006 Propagation of low-mode internal waves through the ocean. J. Phys. Oceanogr. 36, 1220–1236.Google Scholar
Rodenborn, B., Keifer, D., Zhang, H. P. & Swinney, H. L. 2011 Harmonic generation by reflecting internal waves. Phys. Fluids 23, 026601.Google Scholar
Smith, S. & Crockett, J. 2014 Experiments on nonlinear harmonic generation from colliding internal wave beams. Exp. Fluids Thermal Sci. 54, 93–101.Google Scholar
Sutherland, B. R. 2016 Excitation of superharmonics by internal modes in a non-uniformly stratified fluid. J. Fluid Mech. 793, 335–352.Google Scholar
Tabaei, A. & Akylas, T. R. 2003 Nonlinear internal gravity beams. J. Fluid Mech. 482, 141–161.Google Scholar
Tabaei, A., Akylas, T. R. & Lamb, K. G. 2005 Nonlinear effects in reflecting and colliding internal wave beams. J. Fluid Mech. 526, 217–243.Google Scholar
Thorpe, S. A. 1998 Nonlinaer reflection of internal waves at a density discontinuity at the base of a mixed layer. J. Phys. Oceanogr. 28, 1853–1860.2.0.CO;2>CrossRefGoogle Scholar
Wunsch, S. 2015 Nonlinear harmonic generation by diurnal tides. Dyn. Atmos. Oceans 71, 91–97.Google Scholar
Wunsch, S. & Brandt, A. 2012 Laboratory experiments on internal wave interactions with a pycnocline. Exp. Fluids 53, 1663–1679.CrossRefGoogle Scholar
Wunsch, S., Delwiche, I., Frederick, G. & Brandt, A. 2015 Experimental study of nonlinear harmonic generation by internal waves incident on a pycnocline. Exp. Fluids 56, 87.Google Scholar
Wunsch, S., Ku, H., Delwiche, I. & Awadallah, R. 2014 Simulation of nonlinear harmonic generation by an internal wave beam incident on a pycnocline. Nonlinear Process. Geophys. 21, 855–868.CrossRefGoogle Scholar
Xie, X., Chen, G., Shang, X. & Fang, W. 2008 Evolution of the semidiurnal (m 2 ) internal tide on the continental slope for the borthen south china sea. Geophys. Res. Lett. 35, L13604.Google Scholar
Xie, X., Shang, X., van Haren, H. & Chen, G. 2013 Observations of enhanced nonlinear instability in the surface reflection of internal tides. Geophys. Res. Lett. 40, 1580–1586.Google Scholar
Zhao, Z., Alford, M. H., Girton, J. B., Rainville, L. & Simmons, H. L. 2016 Global observations of open-ocean mode-1 m 2 internal tides. J. Phys. Oceanogr. 46, 1657–1684.Google Scholar
Zhou, Q. & Diamessis, P. J. 2013 Reflection of an internal gravity wave beam off a horizontal free-slip surface. Phys. Fluids 25, 036601.Google Scholar