Hostname: page-component-7479d7b7d-68ccn Total loading time: 0 Render date: 2024-07-08T20:13:12.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Approach and separation of quantised vortices with balanced cores

Published online by Cambridge University Press:  04 November 2016

C. Rorai Open the ORCID record for C. Rorai [Opens in a new window] ,
J. Skipper ,
R. M. Kerr  and
K. R. Sreenivasan
C. Rorai*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
J. Skipper
Affiliation:
Department of Mathematics, University of Warwick, Coventry CV4 7AL, UK
R. M. Kerr
Affiliation:
Department of Mathematics, University of Warwick, Coventry CV4 7AL, UK
K. R. Sreenivasan
Affiliation:
Tandon School of Engineering, New York University, 15 Metro Tech Center, New York City, NY 11201, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The scaling laws for the reconnection of isolated pairs of quantised vortices are characterised by numerically integrating the three-dimensional Gross–Pitaevskii equations, the simplest mean-field equations for a quantum fluid. The primary result is the identification of distinctly different temporal power laws for the pre- and post-reconnection separation distances 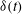$\unicode[STIX]{x1D6FF}(t)$ for two configurations. For the initially anti-parallel case, the scaling laws before and after the reconnection time 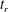$t_{r}$ obey the dimensional 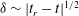$\unicode[STIX]{x1D6FF}\sim |t_{r}-t|^{1/2}$ prediction with temporal symmetry about 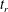$t_{r}$ and physical space symmetry about the mid-point between the vortices 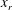$x_{r}$. The extensions of the vortex lines close to reconnection form the edges of an equilateral pyramid. For all of the initially orthogonal cases, 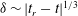$\unicode[STIX]{x1D6FF}\sim |t_{r}-t|^{1/3}$ before reconnection and 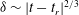$\unicode[STIX]{x1D6FF}\sim |t-t_{r}|^{2/3}$ after reconnection are respectively slower and faster than the dimensional prediction. For both configurations, smooth scaling laws are generated due to two innovations. The first innovation is to use an initial low-energy vortex-core density profile that suppresses unwanted density fluctuations as the vortices evolve in time. The other innovation is the accurate identification of the position of the vortex cores from a pseudo-vorticity constructed on the three-dimensional grid from the gradients of the wave function. These trajectories allow us to calculate the Frenet–Serret frames and the curvature of the vortex lines, secondary results that might hold clues for the origin of the differences between the scaling laws of the two configurations. Reconnection takes place in a reconnection plane defined by the average tangents 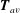$\boldsymbol{T}_{av}$ and curvature normal 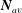$\boldsymbol{N}_{av}$ directions of the pseudo-vorticity curves at the points of closest approach, at time $t\approx t_{r}$. To characterise the structure further, lines are drawn that connect the four arms that extend from the reconnection plane, from which four angles 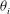$\unicode[STIX]{x1D703}_{i}$ between the lines are defined. Their sum is convex or hyperbolic, that is 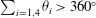$\sum _{i=1,4}\unicode[STIX]{x1D703}_{i}>360^{\circ }$, for the orthogonal cases, as opposed to the acute angles of the pyramid found for the anti-parallel initial conditions.

JFM classification

Complex Fluids: Quantum fluids Vortex Flows: Vortex dynamics Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 808 , 10 December 2016 , pp. 641 - 667
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berloff, N. G. 2004 Interactions of vortices with rarefaction solitary waves in a Bose–Einstein condensate and their role in the decay of superfluid turbulence. Phys. Rev. A 69, 053601.CrossRefGoogle Scholar
Bewley, G. P., Paoletti, M. S., Sreenivasan, K. R. & Lathrop, D. P. 2008 Characterization of reconnecting vortices in superfluid helium. Proc. Natl Acad. Sci. USA 105, 13707–13710.CrossRefGoogle ScholarPubMed
Boratav, O. N., Pelz, R. B. & Zabusky, N. J. 1992 Reconnection in orthogonally interacting vortex tubes: direct numerical simulations and quantification in orthogonally interacting vortices. Phys. Fluids A 4, 581–605.CrossRefGoogle Scholar
de Waele, A. T. A. M. & Aarts, R. G. K. M. 1994 Route to vortex reconnection. Phys. Rev. Lett. 72, 482–485.Google Scholar
Fetter, A. L. 1969 Lectures in Theoretical Physics: Quantum Fluids and Nuclear Matter, volume XIB (ed. Mahanthappa, K. T. & Brittin, W. E.), p. 351. Gordon & Breach Science Pub.Google Scholar
Hussain, F. & Duraisamy, K. 2011 Mechanics of viscous vortex reconnection. Phys. Fluids 23, 021701.Google Scholar
Kerr, R. M. 2011 Vortex stretching as a mechanism for quantum kinetic energy decay. Phys. Rev. Lett. 106, 224501.Google Scholar
Kerr, R. M. 2013 Swirling, turbulent vortex rings formed from a chain reaction of reconnection events. Phys. Fluids 25, 065101.CrossRefGoogle Scholar
Koplik, J. & Levine, H. 1993 Vortex reconnection in superfluid helium. Phys. Rev. Lett. 71, 1375–1378.Google Scholar
Kursa, M., Bajer, K. & Lipniacki, T. 2011 Cascade of vortex loops initiated by a single reconnection of quantum vortices. Phys. Rev. B 83, 014505.Google Scholar
Leadbeater, M., Samuels, D. C., Barenghi, C. F. & Adams, C. S. 2003 Decay of superfluid turbulence via Kelvin-wave radiation. Phys. Rev. A 67, 015601.Google Scholar
Leadbeater, M., Winiecki, T., Samuels, D. C., Barenghi, C. F. & Adams, C. S. 2001 Sound emission due to superfluid vortex reconnections. Phys. Rev. Lett. 86, 1410–1413.Google Scholar
Meichle, D. P., Rorai, C., Fisher, M. E. & Lathrop, D. P. 2012 Quantized vortex reconnection: Fixed points and initial conditions. Phys. Rev. B 86, 014509.CrossRefGoogle Scholar
Nazarenko, S. & West, R. 2003 Analytical solution for nonlinear Schrödinger vortex reconnection. J. Low Temp. Phys. 132, 1–10.Google Scholar
Paoletti, M. S., Fisher, M. E., Sreenivasan, K. R. & Lathrop, D. P. 2008 Velocity statistics distinguish quantum from classical turbulence. Phys. Rev. Lett. 101, 154501.Google Scholar
Rorai, C. 2012 Vortex Reconnection in Superfluid Helium. University of Trieste.Google Scholar
Rorai, C., Sreenivasan, K. R. & Fisher, M. E. 2013 Propagating and annihilating vortex dipoles in the Gross–Pitaevskii equation. Phys. Rev. B 88, 134522.CrossRefGoogle Scholar
Sasa, N., Kano, T., Machida, M., L’vov, V. S., Rudenko, O. & Tsubota, M. 2011 Energy spectra of quantum turbulence: large-scale simulation and modeling. Phys. Rev. B 84, 054525.CrossRefGoogle Scholar
Schwarzschild, B. 2010 Three-dimensional vortex dynamics in superfluid 4 He: homogeneous superfluid turbulence. Phys. Today 2010, 1214.Google Scholar
Skrbek, L. & Sreenivasan, K. R. 2012 Developed quantum turbulence and its decay. Phys. Fluids 24, 011301.Google Scholar
Tebbs, R., Youd, A. J. & Barenghi, C. F. 2011 The approach to vortex reconnection. J. Low Temp. Phys. 162, 314–321.Google Scholar
Walmsley, P. M. & Golov, A. I. 2008 Quantum and quasiclassical types of superfluid turbulence. Phys. Rev. Lett. 100, 245301.Google Scholar
Zuccher, S., Caliari, M., Baggaley, A. W. & Barenghi, C. F. 2012 Quantum vortex reconnections. Phys. Fluids 24, 125108.CrossRefGoogle Scholar