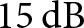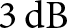Introduction
An earlier version of this paper was presented at the 2023 20th European Radar Conference and was published in its Proceedings [Reference Hofstadler, Larcher, Feger, Springer and Stelzer1].
The concept of joint communication and sensing (JCAS) was introduced over two decades ago [Reference Hughes and Choe2]. The 5G New Radio (NR) standard, defined by the 3rd Generation Partnership Project (3GPP), encompasses the frequency range 2 (FR2), spanning from 24.25 to 52.6 GHz. This higher frequency range facilitates greater bandwidths, generating significant interest in JCAS. The upcoming 6G cellular standard, which actively explores sensing capabilities, further amplifies the potential of this research area [Reference Zhao, Lister, Saxena and Erfanian3]. However, JCAS presents challenges, such as balancing communication and sensing performance.
Current research predominantly focuses on vehicular or network-side JCAS [Reference Wymeersch, Seco-Granados, Destino, Dardari and Tufvesson4] and studies ranging from broad network-wide concepts [Reference Wild, Braun and Viswanathan5] to detailed performance analyses within base station (BS) [Reference Dong, Wang, Hu and Hui6].
Our research focuses on user equipment (UE)-side JCAS to estimate the range and velocity of nearby objects using existing 5G infrastructure. This can provide data which are typically obtained through camera or laser sensors. Laser sensors need extra hardware and power, while cameras are not light-independent. Our JCAS method uses existing signals, requiring no extra hardware or modification of the standard and uniquely providing direct Doppler information.
We utilize the sounding reference signal (SRS) for UE-side JCAS. Initially introduced inLong Term Evolution (LTE), SRS is periodically transmitted by UEs to help BSs estimate channel characteristics. We will elaborate on this signal in the next section.
However, the 5G NR standard allows for various resource allocations for SRS within the 5G orthogonal frequency division multiplexing (OFDM) resource grid, leading to potentially sparse and nonuniformly distributed resources for sensing. This can significantly reduce sensing performance, resulting in a distorted range-velocity map with varying sidelobes. Sensing performance often benefits from windowing, which suppresses sidelobes and enables the detection of targets obscured by these sidelobes. Traditional window or filter coefficients may underperform due to the properties of SRS.
To address this, we present a method to improve sensing performance using optimized window coefficients tailored to sparse and unevenly distributed resources through a convex optimization approach. This study evaluates the impact of these optimized coefficients. To our knowledge, convex optimization for window functions is applied only in [Reference Keskin, Tigrek, Aydogdu, Lampel, Wymeersch, Alvarado and Willems7] for JCAS and in [Reference Liu, Wang and Song8] for SAR imaging. However, both works do not address 2D signals for range and Doppler processing, and more importantly, they do not consider nonuniform resource distributions.
The 5G resource grid and the SRS
The 5G resource grid
5G uses OFDM as transmission scheme both in downlink and uplink (UL) with orthogonal frequency division multiple access (OFDMA) as multiple access scheme.Footnote 1 With OFDMA data to be transmitted to or from a user are allocated for transmission by specifying time (i.e. the respective OFDM symbol or time slot) and frequency (i.e. the respective subcarriers of an OFDM symbol). We thus have a two-dimensional resource grid in 5G in which we can allocate resources (i.e. complex data symbols) in time and frequency for communication and sensing [9]. The smallest resource units we consider are so-called resource blocks. A resource block is a group of 
$N_{\mathrm{sc}}^{\mathrm{RB}}=12$ consecutive subcarriers within one OFDM symbol that are allocated to a user [10]. In this work, we consider the time period of one radio subframe with a duration of 1 ms. In this time period, several resources blocks can be allocated. The maximum number of resource blocks available within this period is denoted by 
$N_{\mathrm{RB}}$. This number depends on the specific application and the network requirements.
The 5G standard enables highly dynamic resource allocation, allowing for real-time adaptation to changing network conditions, radio channel, and user requirements. This dynamic allocation enables efficient sharing of resources between different users and applications, improving the overall system performance, but can lead to various different resource allocations for one UE from almost full, down to sparse resources available for range and velocity estimation. In the latter case, reduced sensing performance might result in scenarios where a target is obscured by the sidelobes of, e.g., the TX/RX leakage present in every radar system.
This work is based on release 17 of the 5G 3GPP standard [10]. Key values for the resource grid, such as the subcarrier spacing and the number of symbols per subframe are defined by the so-called numerology parameter µ. For this work µ = 3 is chosen, which is a typical FR2 configuration. This leads to a subcarrier spacing of 
$\Delta f = 2^{\mu} \cdot 15 \, \mathrm{kHz} = 120 \, \mathrm{kHz}$.
The number of OFDM symbols per subframe therefore is 
$N_{\mathrm{symb}}^{\mathrm{sub}} = 112$. The number of available resource blocks 
$N_{\mathrm{RB}}$ for allocation is selected in accordance with the available computational resource to 
$N_{\mathrm{RB}} = 24$.
Figure 1(a) shows an exemplary allocated resource grid for 
$N_{\mathrm{RB}} = 24$ and 
$N_{\mathrm{symb}}^{\mathrm{sub}} = 112$. The black rectangles represent resources allocated for the SRS. White areas represent resources not allocated to the SRS. This exemplary SRS allocation shows that the resources are allocated non-uniformly across time and frequency. In addition, the zoomed in view on the subcarrier allocation in Fig. 1(b) shows that, depending on the comb number 
$K_{\mathrm{TC}}$, which will be discussed in the next subsection, only every 
$K_{\mathrm{TC}}$th subcarrier is used for the SRS in areas of the resource grid allocated for the SRS.
Figure 1. Resource grid allocation for the selected SRS signal configuration: (a) the entire grid; (b) a zoomed in view of some subcarriers along a OFDM symbol, shown by the red arrow. The black segments represent allocated resource elements.
The sounding reference signal
The SRS is used for channel estimation and is sent in the UL. Therefore, it is sent periodically also in situations when no user data is sent. It is based on a low peak-to-average power ratio (PAPR) sequence. Depending on the length of the sequence it is either a Zadoff–Chu sequence or a numerically derived sequence with properties which fulfill the requirements of the standard similarly as the Zadoff–Chu sequence does [9]. Therefore, the SRS sequence is a constant-amplitude zero-autocorrelation sequence. The PAPR characteristic is also beneficial for the transmit signal, as the PAPR of the resulting waveform is limited, and thus the requirements on the transceiver are lower, compared to an OFDM transmit signal carrying a random bit stream.
The sequence is allocated in the resource grid according to the comb number 
$K_{\mathrm{TC}} \in \{2,4,8\}$, along the axis of the frequency resources [9]. This number defines that every 
$K_{\mathrm{TC}}$th subcarrier is used for SRS sequence allocation. Figure 1 shows a SRS sequence, with 
$K_{\mathrm{TC}}=2$. The detailed allocation pattern resulting from this comb number can be seen in Fig. 1(b). This also means that even if the subcarrier spacing is 
$\Delta f =$ 120 kHz, the smallest frequency difference for a single SRS sequence is 
$\operatorname{min}(K_{\mathrm{TC}}) \Delta f =$ 240 kHz. The sequence can allocate resources in 
$N_{\mathrm{symb}}^{\mathrm{SRS}} \in \{1, 2, 4,8,10,12,14\}$ consecutive OFDM symbols per slot [9]. Figure 1 shows an SRS sequence configuration, for 
$N_{\mathrm{symb}}^{\mathrm{SRS}} =4$.
The number of resource blocks which are allocated, 
$N_{\mathrm{{allo}}}$, can be calcuated with the number of OFDM symbols 
$N_{\mathrm{{allo}}}^{\mathrm{symb}}$, in which any resource blocks are allcoated and the number of allocated resource blocks within one OFDM symbol 
$N_{\mathrm{{allo}}}^{\mathrm{RB}}$ with [9] 
$N_{\mathrm{{allo}}}=N_{\mathrm{{allo}}}^{\mathrm{symb}} \cdot N_{\mathrm{{allo}}}^{\mathrm{RB}}$. Figure 1 shows a resource grid with 
$N_{\mathrm{{allo}}}^{\mathrm{symb}}=32$ and 
$N_{\mathrm{{allo}}}^{\mathrm{RB}}=4$.
The SRS is also used in the so-called beam mobility procedure. As beamforming is part of 5G NR, selecting the best beam for transmission is of high interest for both link partners. Within this UL procedure, the BS performs power measurements, while the UE is transmitting the SRS on one or more beams [Reference Kottkamp, Pandey, Raddino, Roessler and Stuhlfauth11]. Thus, the SRS could be used in a similar manner for UE-side sensing, while exploiting the behavior that the signal is intended to be used in the 3GPP 5G standard. This makes it a promising candidate for UE-side JCAS.
OFDM-based sensing, windowing, and convex optimization
OFDM-based sensing
The concept of OFDM-based sensing is well-known [Reference Braun12]. The individual resource allocation is one challenge for embedding sensing into an existing communication standard based on OFDM. Processing an entire subframe at once, e.g. the one in Fig. 1, result in significantly different range-velocity maps, as the data which is Fourier transformed is distributed non-uniformly and shows gaps within the data. This requires individual signal processing measures, for each grid.
Communication in FR2 is based on time division duplex, but for radar the UE needs to transmit and receive at the same time. Furthermore, different to a TRX designed only for communication, the radar TX and RX chains need to be synchronized both in time and frequency.
To realize range and velocity estimation, the received signal is first demodulated to the received symbols. Those are then divided element wise by the TX symbols to remove the communication related phase information, which results in the symbol matrix 
$\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}$. 
$\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}$ only contains the channel related phase information. Performing an inverse Fourier transform along the columns and a Fourier transform along the rows leads to the range-velocity map which can be calculated, e.g., by [Reference Donnet and Longstaff13]
\begin{align}
\mathbf{D}=
\left[
\mathbf{F_{\mathrm{d}}}
\left(
\mathbf{F}_{\tau}
\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}
\right)^{\mathrm{T}}
\right]^{\mathrm{T}}
=
\mathbf{F}_{\tau}
\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}
\mathbf{F_{\mathrm{d}}}^{\mathrm{T}}
,
\end{align} where D is the range-velocity map, 
$\mathbf{F}_{\tau}$ is the inverse discrete Fourier transform (IDFT) matrix for the IDFT along the subcarriers, and 
$\mathbf{F_{\mathrm{d}}}$ is the discrete Fourier transform (DFT) matrix for the DFT along the OFDM symbols.
In some sensing scenarios, e.g. a multi-target scenario, the sidelobe level (SLL) of the target peaks is crucial. The sidelobes of one peak might cover other peaks of interest, especially with nonuniformly distributed resources, which can introduces diagonally located special sidelobes as it can be seen in Fig. 4(a). Windowing can help here to reduce the SLL of each peak and therefore help to correctly identify all targets.
Conventional window coefficients
Conventional two-dimensional window coefficients can be multiplied with a Hadamard product to 
$\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}$ before the Fourier transformation, to reduce the SLL and achieve improved target detection in the range-velocity map. This can be described with
\begin{align}
\mathbf{D}=
\mathbf{F}_{\tau}
\left(
\mathbf{W}_{\mathrm{g}} \circ \mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}
\right)
\mathbf{F_{\mathrm{d}}}^{\mathrm{T}}
,
\end{align} where 
$\mathbf{W}_{\mathrm{g}}$ is a matrix containing the window coefficients, and 
$\circ$ is the Hadamard product.
For the IDFT along the subcarriers, a conventional windowing approach could be directly feasible, as the frequency resources are allocated in a homogeneous pattern (
$K_{\mathrm{TC}}=2$), but for the DFT along the OFDM symbols such an approach is not directly feasible, because the resources are allocated inhomogeneously. However, also for the velocity dimension optimized window coefficients, which are tailored to the respective resource allocation, will result in a reduced SLL. We thus intend to find an efficient method to compute optimized coefficients also for the velocity dimension. Furthermore, we intend to find fully 2D optimized coefficients and compare their SLL performance.
Row-wise optimization of window coefficients
We want to find window coefficients which are optimized for velocity estimation using the SRS transmitted and received by the UE. For that we consider a specific resource grid allocation and optimize the window coefficients for it.
We have exemplary selected the SRS allocation shown in Fig. 1, because on one hand all possible frequency resources are allocated. But on the other hand for each OFDM symbol only a fraction of the frequency resources is allocated.
As it can be seen the optimization problem turns out to be convex, such that we can make use of the Python-based CVXPY package [Reference Diamond and Boyd14]. The linearity of the Fourier transform allows to perform the optimization for a one target scenario, e.g. one target peak position in the range and velocity profiles, and still the optimized window coefficients are then applicable to all target positions and velocities. Therefore, the trivial case of a target with range r = 0 and velocity v = 0 is chosen here. All allocated elements of 
$\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}$ then become ones. The size of 
$\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}$ is 
$\left(N_{\mathrm{sc}}^{\mathrm{RB}} \cdot N_{\mathrm{RB}}\right) \times N_{\mathrm{symb}}^{\mathrm{sub}} = 288 \times 112$, which is a total of 
$32,256$ resource elements. Without any additional measures, this would be computationally very demanding for a conventional optimization. Furthermore, in the case of the resource grid of Fig. 1, the number of allocated resource elements is only 
$N_{\mathrm{{allo}}}\cdot N_{\mathrm{sc}}^{\mathrm{RB}} / K_{\mathrm{TC}} =768$. All other elements are zero, leaving only 2.4% non-zero elements in 
$\mathbf{W}_{\mathrm{g}}$. To reduce the computational effort we used a simplified approach, where independent one-dimensional window coefficients are used for the rows. For the optimization of this coefficients along the OFDM symbols first
\begin{equation}
\begin{aligned}
\mathbf{D}_{\tau}
=
\mathbf{F}_{\tau}
\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}
\end{aligned}
\end{equation} is computed. In the context of OFDM, the analysis of range profiles across the rows for each symbol is simplified by computing the absolute value of each element of 
$\mathbf{D}_{\tau}$, which focuses on identifying if there was subcarrier allocation present or absent in the resource grid, disregarding phase variations.
Each row of 
$|\mathbf{D}_{\tau}|$ features the same number of non-zero elements at the same indices, with the same absolute value. For this optimization method, only a single representative row is needed. Selecting the row which represents the zero delay profile peak serves best to ensure that the scaling of the optimized coefficients is in accordance with preserving the target peak height throughout the optimization. The selected row d is windowed according to 
$\mathbf{w}_{\mathrm{d}} \circ \mathbf{d}$, which serves as input for the optimization of the window coefficient vector 
$\mathbf{w}_{\mathrm{d}}$, to minimize the SLL of the velocity profile.
The velocity profile is derived using 
$\mathbf{F}_{\mathrm{d}} (\mathbf{w}_{\mathrm{d}} \circ \mathbf{d})$. To enhance computational efficiency, entries in d that are zero, and consequently the corresponding entries in 
$\mathbf{w}_{\mathrm{d}}$ and the related columns of 
$\mathbf{F}_{\mathrm{d}}$, can be disregarded, as they do not contribute to the optimization outcome. 
$\mathbf{d}^{\prime}$, 
$\mathbf{w}_{\mathrm{d}}^{\prime}$, and 
$\mathbf{F}_{\mathrm{d}}^{\prime}$ are the vectors and the matrix without zero entries. Notably, 
$\mathbf{d}^{\prime}$ consists only of the values 
$N_{\mathrm{{allo}}}^{\mathrm{RB}} \cdot N_{\mathrm{sc}}^{\mathrm{RB}} / K_{\mathrm{TC}} =24$ and can be completely excluded from the optimization process, as it merely multiplies a constant factor to the optimized coefficients. Consequently, the convex optimization problem to find the optimal values 
$\mathbf{w}_{\mathrm{opt}}$ can be formulated as [Reference Boyd and Vandenberghe15]
\begin{equation}
\begin{aligned}
\mathrm{\mathbf{w}_{opt}} = \underset{\mathbf{w}_{\mathrm{d}}^\prime}{\mathrm{arg\,min}}
\quad & \max(\tilde{\mathbf{F}}_{\mathrm{d}}^{\prime} \mathbf{w}_{\mathrm{d}}^{\prime})\\
\textrm{subject to} \quad & \textstyle{\sum_{\mathbf{w}_{\mathrm{d}}^{\prime}}}= N_{\mathrm{{allo}}}\cdot N_{\mathrm{sc}}^{\mathrm{RB}}\\
\quad & \mathrm{abs}(\mathbf{w}_{\mathrm{d}}^{\prime}[i+1]-\mathbf{w}_{\mathrm{d}}^{\prime}[i])\leq \varepsilon\\
\qquad & \forall i \in \{1, 2, \ldots, L-1\}.
\end{aligned}
\end{equation} The notation 
$\tilde{(\cdot)}$ signifies that 
$\mathbf{F_{\mathrm{d}}}$ has been selectively masked to nullify all rows except those within the velocity range targeted for optimization. The boundary of this mask should be at least set at 
${21}\,{\mathrm{m~s}^{-1}}$ (approximately 
${75}\,{\mathrm{km~h}^{-1}}$), matching the unambiguous region of the velocity profile, but not come too close to an alias peak. Consequently, the rows of 
$\tilde{\mathbf{F_{\mathrm{d}}^{\prime}}}$ representing velocities outside this limit are excluded from the optimization process, as are the rows corresponding to the main lobe. This further simplifies the optimization.
The initial constraint in (4) ensures the exclusion of trivial solutions and maintaining the peak position throughout the optimization process. Furthermore, this constraint ensures that the windowed profiles have the same mainlobe gain as a rectangular window. This constraint also implicitly addresses the removal of 
$\mathbf{d}^{\prime}$. The second constraint guarantees that the absolute difference between two successive coefficients, of all L elements in 
$\mathbf{d}^{\prime}$ does not exceed a predefined threshold ɛ. This is crucial for preventing solutions that oscillate around zero, which, while adhering to the first constraint, would not preserve the integrity of the target peak during optimization, as they shift the peak away from its unwindowed position.
The calculated window coefficients obtained from the optimization have to be mapped to the allocated resource element positions of the according SRS configuration to get the two-dimensional row-wise optimized coefficients 
$\mathbf{W}_{\mathrm{opt}}$, with 
$
\mathbf{W}_{\mathrm{opt}} =
\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}
\cdot
\mathrm{diag}(\mathbf{w}_{\mathrm{opt}})
$. The optimized range-velocity 
$\mathbf{D}_{\mathrm{w}}$ map can then be calculated according to
\begin{align}
\mathbf{D}_{\mathrm{w}}=
\mathbf{F}_{\tau}
\left(
\mathbf{W}_{\mathrm{opt}} \circ \mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}
\right)
\mathbf{F_{\mathrm{d}}}^{\mathrm{T}}
.
\end{align}Full 2D optimization of window coefficients
While the proposed row-wise optimization significantly reduces computational effort and can be expected to achieve decent sidelobe suppression along the velocity profile of a target, it unfortunately does not possess the capability to optimize a full 2D range-velocity map in its entirety. Given the sparse nature of the resource grid, special sidelobe peaks appear in the map. Additionally, due to the resources being distributed in a diagonal-like pattern, these special sidelobe peaks tend to be located along diagonal lines through the target peak and not only along its range and velocity dimensions. Unfortunately, the proposed row-wise method does not successfully minimize these diagonally located peaks. The motivation behind proposing this method was primarily its computability advantages.
To effectively tackle full 2D optimization, significant preprocessing steps are required to minimize the computational effort to a level at which it becomes feasible.Footnote 2
Handling the computational challenges associated with (5), it is necessary to adapt the problem formulation into a more optimization-friendly structure. As only 
$2.4\%$ of the elements in 
$\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}$ are non-zero, we need a method that leverages this sparse nature.
As noted in [Reference Henderson and Searle16], for a matrix equation represented by 
$\mathrm{\mathbf{AXB}=\mathbf{C}}$, there exists an equivalent relation formulated as:
\begin{align}
\mathrm{\mathbf{B^{T}}} \otimes \mathrm{\mathbf{A}} \cdot \mathrm{vec}(\mathrm{\mathbf{X}}) = \mathrm{vec}(\mathrm{\mathbf{C}}).
\end{align} In this formulation, ⊗ denotes the Kronecker product, and 
$\mathrm{vec}(\cdot)$ represents the vectorization of a two-dimensional matrix. Vectorization rearranges the matrix by stacking its columns to form a single column vector, transforming an original matrix of dimension M × N into a vector of length MN. This approach effectively reduces the size of the problem, making it more tractable for optimization by utilizing the sparseness of 
$\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}$.
The original matrix 
$\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}$ is vectorized with 
${\boldsymbol{\Phi}}_{\mathrm{RX}}^{\mathrm{ch}}=
\mathrm{vec}
\left(
\mathbf{Y_{\mathrm{RX}}^{\mathrm{ch}}}
\right)$. This step is also applied to the window coefficient matrix 
$\mathrm{\mathbf{W}_{\mathrm{opt}}}$, denoted by 
${\boldsymbol{\Psi}}_{\mathrm{opt}}=\mathrm{vec}(\mathbf{W}_{\mathrm{opt}})$, and to the range-velocity map, expressed as 
$\boldsymbol{\Delta}_{\mathrm{w}}=\mathrm{vec}(\mathbf{D}_{\mathrm{w}})$. Consequently, (5) can be reformulated in a vectorized form as:
\begin{align}
\boldsymbol{\Delta}_{\mathrm{w}}=
\mathbf{F_{\mathrm{d}}} \otimes \mathbf{F}_{\tau}
\left(
\boldsymbol{\Psi}_{\mathrm{opt}} \circ \boldsymbol{\Phi}_{\mathbf{{\mathrm{RX}}^{\mathrm{ch}}}}
\right).
\end{align} From 
$\boldsymbol{\Delta}_{\mathrm{w}}$, the range-velocity map 
$\mathbf{D}_{\mathrm{w}}$ can be calculated through 
$\mathbf{D}_{\mathrm{w}} =\mathrm{vec}^{-1}(\boldsymbol{\Delta}_{\mathrm{w}})$, where 
$\mathrm{vec}^{-1}(\cdot)$ is the inverse operation of 
$\mathrm{vec}(\cdot)$, transforming the vectorized form back into the original two-dimensional matrix.
To target relevant portions of the range-velocity map during the optimization, 
$\mathbf{F_{\mathrm{d}}}$ and 
$\mathbf{F}_{\tau}$ must be masked. Unlike the row-wise optimization approach, where masking can be directly applied to individual matrices (as demonstrated with 
$\tilde{\mathbf{F_{\mathrm{d}}}}$), the masking in this context requires an element-wise multiplication. This is achieved using a mask matrix 
$\boldsymbol{\Omega}$, which is applied from the left side with the Hadamard product to (5), or a matrix 
$\boldsymbol{\Omega}_{\mathrm{kron}}$, where each column is a copy of the vectorized mask 
$\mathrm{vec}(\boldsymbol{\Omega})$ for (7), resulting in:
\begin{align}
\boldsymbol{\Gamma} = \boldsymbol{\Omega}_{\mathrm{kron}} \circ (\mathbf{F_{\mathrm{d}}} \otimes \mathbf{F}_{\tau}).
\end{align}This ensures that only designated areas of the range-velocity map undergo optimization, focusing computational resources on regions of interest and thereby enhancing the efficiency and effectiveness of the optimization.
An example configuration of the mask 
$\boldsymbol{\Omega}$ is illustrated in Fig. 2, where it is overlaid on an example range-velocity map. The areas of 
$\boldsymbol{\Omega}$ set to ones, i.e. the areas which should be optimized, are represented in violet, while areas set to zero, i.e. the areas which should not be optimized, are transparent. This mask is constructed from two rectangular regions: an outer rectangle defines the overall area subject to optimization, and an inner rectangle excludes the vicinity around the target peak from the optimization. Figure 2(a) displays the full extent of the map, and Fig. 2(b) focuses on the area surrounding the target peak.
Figure 2. Entire optimization mask (a) and a zoomed in version around the target peak area (b). The shape of the mask is illustrated overlaying a range-velocity map for orientation purpose. The areas of the mask set to ones, i.e. the areas which should be optimized, are represented in violet, while areas set to zero, i.e. the areas which should not be optimized, are transparent.
Given that 
$K_{\mathrm{TC}}=2$, an alias along the range axis can be seen at the map’s boundary, indicating that the unambiguity range covers half the map’s extent. Thus, the mask must at least cover this unambiguity range. However, to avoid oscillatory solutions from the optimization, we need to extend the mask further, as can be seen in Fig. 2(a).
The mask’s size along the velocity axis is the same size used in the row-wise optimization method, which is approximately 21 m/s.
Also, the dimensions of the inner rectangle are similarly aligned with those employed in the row-wise optimization method.
Furthermore, any zero-valued elements within 
$\boldsymbol{\Psi} \circ \boldsymbol{\Phi}_{\mathbf{{\mathrm{RX}}^{\mathrm{ch}}}}$ and the respective columns in 
$\boldsymbol{\Gamma}$ again do not have an impact on the optimization process and can be excluded. This exclusion is again marked with 
$(\cdot)^{\prime}$.
Additionally, within 
$\boldsymbol{\Gamma}$, rows resulting in zeros due to the application of the mask can also be disregarded. This process of elimination is symbolized with 
$(\cdot)^{\dagger}$. Similar to the row-wise optimization approach, 
$\boldsymbol{\Phi}_{\mathbf{{\mathrm{RX}}^{\mathrm{ch}}}}^{\prime}$, now essentially a vector of ones, can be completely omitted. This combination of simplifications not only reduces computational complexity but also ensures that the optimization focuses on reducing the SLL within the masked area.
Finally the optimization problem can be written as
\begin{equation}
\begin{aligned}
\boldsymbol{\Psi}^{\prime}_{\mathrm{opt}} = \underset{\boldsymbol{\Psi}^{\prime}}{\mathrm{arg\,min}}
\quad & \max(\boldsymbol{\Gamma}^{\dagger} \cdot \boldsymbol{\Psi}^{\prime})\\
\textrm{subject to} \quad & \textstyle{\sum_{\boldsymbol{\Psi}^{\prime}_{\mathrm{opt}}}} =N_{\mathrm{{allo}}}\cdot N_{\mathrm{sc}}^{\mathrm{RB}}.
\end{aligned}
\end{equation}The constraint is designed to avoid trivial solutions and result in a mainlobe gain which is the same as for a rectangular window. To mitigate oscillating behaviors, the choice of an appropriate mask has been identified as the sole viable strategy, given that applying a similar constraint as used in the row-wise approach proved to be unfeasible for this work.
Results
Figure 3(a) illustrates the simulated normalized range profiles, while Fig. 3(b) depicts the normalized velocity profiles and Fig. 3(c) shows the normalized diagonal profiles, of the trivial target as sensed via the resource grid presented in Fig. 1. In all figures, the profiles derived from a range-velocity map utilizing unwindowed signal processing are denoted by a blue line. The red lines represent the profiles resulting from a map with the proposed row-wise optimization. The violet lines show the results of the proposed full 2D optimization and the yellow lines represent the results from employing a normalized 2D Hann window. In the range profile, the typical first side lobe level of approx. 
${-30}\,\mathrm{dB}$ of a normalized Hann window can be seen. Conversely, in the velocity profile, the normalized Hann window achieves only a negligible reduction of the peak sidelobe level (PSL). This can be attributed to substantial gaps of the SRS resources in time, as well as the non-uniform resource allocation. This motivated the row-wise optimization approach to enhance the velocity profile. The optimization method, maintains a virtually unchanged behavior in the range profile but achieves a significant improvement in PSL of more than 
${15}\,\mathrm{dB}$ in the velocity profile, alongside a slight increase in the mainlobe width that still remains marginally narrower than that of the normalized Hann window.
Figure 3. Normalized range profiles (a), velocity profiles (b), and diagonal profiles (c). Blue: unwindowed profiles. Red: profiles with row-wise optimization. Violet: profiles with full 2D optimization. Yellow: profiles with normalized 2D Hann window. The diagonal profiles pass exactly through the two diagonally located special sidelobes at ≈(5 m, 17m s−1), with the highest SLL. These locations are highlight with the green dashed arrow in Fig. 4.
On a first glance, the full 2D optimization demonstrates only a marginal improvement in PSL relative to the unwindowed scenario. Nonetheless, the essential performance attained through this method becomes pronounced in the range-velocity map. Figure 4 shows the range-velocity map for each signal processing technique discussed: unwindowed (a), the normalized 2D Hann window (b), the row-wise optimization (c), and the full 2D optimization (d). Figure 4(a) shows the original map, wherein, in addition to the expected sidelobes in both dimensions, additional peaks are marked with green arrows. The dashed arrows specifically showing where the profiles in Fig. 3(c) intersects. These peaks, identified as diagonally located sidelobes, emerge due to the non-uniform resource allocation within the resource grid, making their attenuation non-trivial. In a worst-case scenario, a target close to one of those regions (e.g. at 5 m and 
${-17}\,{\textrm{m\,s}^{-1}}$) would interfere with these sidelobes, leading to reduced estimation performance. Signal processing using the normalized 2D Hann window fails to reduce the level of these peaks. Similarly, the proposed row-wise method proves ineffective in mitigating these peaks. Only the full 2D optimization demonstrates the capacity to reduce the level of these diagonally located sidelobes, with the peak values of these sidelobes reduced by more than 
${3}\,\mathrm{dB}$, as it can be seen while comparing Fig. 4(a) and (d) and also in the diagonal profiles in Fig. 3(c).
Figure 4. Heatmaps of the range-velocity maps, calculated without window (a), with a normalized conventional Hann window (b), with the row-wise optimized window (c), and with the full 2D optimized window (d). Both green solid and dashed arrows highlight diagonally located sidelobes caused by non-uniform resource allocation, with the dashed arrows specifically showing where the profiles in Fig. 3(c) intersects.
Conclusion
For UE-side JCAS employing 5G NR compliant signals, we proposed an optimization of windowing coefficients for the enhanced estimation and detection of targets within the range-velocity map. We made use of the SRS in conjunction with a sequential column-wise IDFT and row-wise DFT for the map computation. Addressing this challenge is complex due to the 5G NR standard’s non-uniform resource grid allocations. Our strategy involved applying optimized window coefficients across the resource grid to mitigate the SLL within the range-velocity map.
This work proposed two distinct optimization methods: first, a row-wise window coefficient optimization, significantly simplifying the computational complexity. This technique notably enhanced the PSL of the velocity profile by over 15 dB, although without addressing the reduction of diagonally located sidelobes. Consequently, we introduced a second, more comprehensive 2D optimization approach. Despite its higher computational complexity, this method tackles the challenge posed by diagonally located sidelobes. We used a combination of simplifications to render this approach computationally viable. This optimization focuses on damping unwanted peaks on a rectangular area in the range-velocity map, instead of lines along the range and velocity profiles. A peak reduction of more than 3 dB could be achieved.
In subsequent research, we aim to incorporate a non-linear signal processing step, employing apodization techniques to further enhance the SLL performance achieved through the comprehensive 2D optimization.
Acknowledgements
The financial support by the Austrian Federal Ministry for Digital and Economic Affairs, the National Foundation for Research, Technology and Development, and the Christian Doppler Research Association is gratefully acknowledged.
Competing interests
The authors declare none.
Michael Hofstadler (Graduate Student Member, IEEE) was born in Linz, Austria, in 1988. He received the Dipl.-Ing. (M.Sc.) degree in technical physics from JKU Linz, Linz, Austria, in 2020. His master’s thesis was written in cooperation with INTEL Linz. Since then, he has been a member of the Institute for Communications Engineering and RF-Systems, JKU Linz. He is currently pursuing a Ph.D. degree with the Christian Doppler Laboratory for Digitally Assisted RF Transceivers for Future Mobile Communications, where he is focusing his research on 5G compliant joint communication and sensing.
Reinhard Feger was born in Kufstein, Austria, in 1980. He received the Dipl.-Ing. (M.Sc.) degree in mechatronics and the Dr. Techn. (Ph.D.) degree in mechatronics from JKU Linz, Linz, Austria, in 2005 and 2010, respectively. In 2005, he joined the Institute for Communications and Information Engineering, JKU Linz, Linz, Austria, as a Research Assistant. In 2007, he became a member of the Christian Doppler Laboratory for Integrated Radar Sensors, JKU Linz. He is currently an Associate Professor with the Institute for Communications Engineering and RF-Systems, JKU Linz. His research interests include radar signal processing, as well as radar system design for industrial and automotive radar sensors. Dr. Feger was recipient of the 2011 Microwave Prize and the 2011 German Microwave Conference Best Paper Award. In 2012, he received the Best Measurement Paper Prize at the European Conference on Antennas and Propagation.
Andreas Stelzer received the Diploma Engineer degree in electrical engineering from the Technical University of Vienna, Austria, in 1994, and the Dr. techn. degree (Ph.D.) in mechatronics from the JKU Linz, Austria, in 2000. In 2003, he became Associate Professor at JKU Linz. Since 2011, he is Full Professor heading the Department for RF-Systems. His research focuses on microwave sensor systems for industrial and automotive applications, integrated sensor concepts, SiGe-based circuit design, RF and microwave subsystems, as well as digital signal processing for sensor signal evaluation. Dr. Stelzer received several awards including the European Microwave Association (EuMA) Radar Prize in 2003, the 2008 IEEE Microwave Theory and Techniques Society (IEEE MTT-S) Outstanding Young Engineer Award, the 2011 German Microwave Conference (GeMiC) Best Paper Award, the 2011 IEEE Microwave Prize, and the Best Paper Award of the International Journal of Microwave and Wireless Technologies (IJMWT) 2016.
Günther Lindorfer (Graduate Student Member, IEEE) was born in Rohrbach, Austria, in 1995. He studied Electronics and Information Technology at the JKU Linz, and received his Dipl.-Ing. degree with distinction in 2023. In March 2023, he joined the Institute for Communication Engineering and RF-systems where he is currently pursuing the Ph.D. degree as part of the Christian Doppler Laboratory for Digitally Assisted RF Transceivers for Future Mobile Communications. His research is focusing on optimized waveforms for 6G JCAS.
Andreas Meingassner (Graduate Student Member, IEEE) received the B.Sc. and M.Sc. degrees from the JKU, Linz, Austria, in 2020 and 2022, respectively. He is currently with the Christian Doppler Laboratory for Digitally Assisted RF Transceivers for Future Mobile Communications, where he is pursuing the Ph.D. degree in Electronics and Information Technology from the JKU.
Andreas Springer (Senior Member, IEEE) received the Dr. techn. (Ph.D.) degree in electrical engineering and the Univ.-Doz. (Habilitation) degree in communications engineering from JKU (JKU), Linz, Austria, in 1996 and 2001, respectively. He became a Full Professor in 2005 and since July 2002, he has been the Head of the Institute for Communications Engineering and Radio Frequency-Systems, JKU. In the Austrian K2 Center for Symbiotic Mechatronics, he serves as a Research Area Coordinator. Since 2017, he is co-leader of the “Christian Doppler Lab for Digitally Assisted RF Transceivers for Future Mobile Communications.” His current research interests are focused on wireless communication systems, single- and multi-carrier communications architectures and algorithms for multi-band/multi-mode transceivers, and wireless sensor networks.
Open access
