Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-25T23:59:39.287Z Has data issue: false hasContentIssue false
  • English
  • Français

KŐNIG’S LINE COLORING AND VIZING’S THEOREMS FOR GRAPHINGS

Part of: Graph theory Measure-theoretic ergodic theory Noncompact transformation groups Set theory Ergodic theory

Published online by Cambridge University Press:  19 September 2016

ENDRE CSÓKA ,
GÁBOR LIPPNER  and
OLEG PIKHURKO
ENDRE CSÓKA
Affiliation:
MTA Alfréd Rényi Institute of Mathematics, Hungarian Academy of Sciences, Budapest H-1053, Hungary; [email protected]
GÁBOR LIPPNER
Affiliation:
Department of Mathematics, Northeastern University, Boston, MA 02115, USA; [email protected]
OLEG PIKHURKO
Affiliation:
Mathematics Institute and DIMAP, University of Warwick, Coventry CV4 7AL, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical theorem of Vizing states that every graph of maximum degree 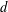$d$ admits an edge coloring with at most 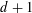$d+1$ colors. Furthermore, as it was earlier shown by Kőnig, 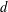$d$ colors suffice if the graph is bipartite. We investigate the existence of measurable edge colorings for graphings (or measure-preserving graphs). A graphing is an analytic generalization of a bounded-degree graph that appears in various areas, such as sparse graph limits, orbit equivalence and measurable group theory. We show that every graphing of maximum degree 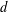$d$ admits a measurable edge coloring with 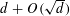$d+O(\sqrt{d})$ colors; furthermore, if the graphing has no odd cycles, then 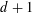$d+1$ colors suffice. In fact, if a certain conjecture about finite graphs that strengthens Vizing’s theorem is true, then our method will show that 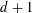$d+1$ colors are always enough.

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs 05C63: Infinite graphs
Secondary: 03E05: Other combinatorial set theory 03E15: Descriptive set theory 22F10: Measurable group actions 28D05: Measure-preserving transformations 37A15: General groups of measure-preserving transformations
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e27
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Abért, M., ‘Some questions’, manuscript available athttp://www.renyi.hu/∼abert/questions.pdf (2010).Google Scholar
Aldous, D. and Lyons, R., ‘Processes on unimodular random networks’, Electron. J. Probab. 12 (2007), 1454–1508.Google Scholar
Benjamini, I. and Schramm, O., ‘Recurrence of distributional limits of finite planar graphs’, Electron. J. Probab. 6 (2001), 13 pages.CrossRefGoogle Scholar
Berge, C. and Fournier, J.-C., ‘A short proof for a generalization of Vizing’s theorem’, J. Graph Theory 15 (1991), 333–336.Google Scholar
Bollobás, B. and Riordan, O., ‘Sparse graphs: metrics and random models’, Random Structures Algorithms 39 (2011), 1–38.Google Scholar
Conley, C. T. and Kechris, A. S., ‘Measurable chromatic and independence numbers for ergodic graphs and group actions’, Groups Geom. Dyn. 7 (2013), 127–180.Google Scholar
Csóka, E. and Lippner, G., ‘Invariant random perfect matchings in Cayley graphs’, Groups Geom. Dyn. (2016), to appear. E-print arXiv:1211.2374.Google Scholar
Elek, G., ‘On limits of finite graphs’, Combinatorica 27 (2007), 503–507.Google Scholar
Elek, G. and Lippner, G., ‘Borel oracles. An analytical approach to constant-time algorithms’, Proc. Amer. Math. Soc. 138 (2010), 2939–2947.Google Scholar
Fournier, J.-C., Un théorème général de coloration, Problèmes combinatoires et théorie des graphes, Orsay 1976, Colloq. int., vol. 260 (CNRS, 1978), 153–155. (French).Google Scholar
Gaboriau, D., ‘Mercuriale de groupes et de relations’, C. R. Acad. Sci. Paris Sér. I Math. 326 (1998), 219–222.Google Scholar
Gaboriau, D., ‘Coût des relations d’équivalence et des groupes’, Invent. Math. 139 (2000), 41–98.CrossRefGoogle Scholar
Gaboriau, D., On Orbit Equivalence of Measure Preserving Actions, Rigidity in Dynamics and Geometry (Cambridge, 2000) (Springer, Berlin, 2002), 167–186.Google Scholar
Gaboriau, D., Orbit Equivalence and Measured Group Theory, Proceedings of the International Congress of Mathematicians, III (Hindustan Book Agency, New Delhi, 2010), 1501–1527.Google Scholar
Gupta, R. P., ‘The chromatic index and the degree of a graph’, Notices Amer. Math. Soc. 13 (1966), 719.Google Scholar
Hatami, H., Lovász, L. and Szegedy, B., ‘Limits of locally-globally convergent graph sequences’, Geom. Funct. Anal. 24 (2014), 269–296.Google Scholar
Kechris, A. S., Classical Descriptive Set Theory, Graduate Texts in Mathematics, 156 (Springer, New York, 1995).Google Scholar
Kechris, A. S., Global Aspects of Ergodic Group Actions, Mathematical Surveys and Monographs, 160 (American Mathematical Society, Providence, RI, 2010).Google Scholar
Kechris, A. S. and Marks, A., Descriptive graph combinatorics, manuscript (2015).Google Scholar
Kechris, A. S. and Miller, B. D., Topics in Orbit Equivalence, Lecture Notes in Mathematics, vol. 1852 (Springer, Berlin, 2004).Google Scholar
Kechris, A. S., Solecki, S. and Todorcevic, S., ‘Borel chromatic numbers’, Adv. Math. 141 (1999), 1–44.CrossRefGoogle Scholar
Kőnig, D., ‘Gráok és alkalmazásuk a determinánsok Žs a halmazok elméleére’, Matematikai és Természettudományi Értestő 34 (1916), 104–119.Google Scholar
Laczkovich, M., ‘Closed sets without measurable matching’, Proc. Amer. Math. Soc. 103 (1988), 894–896.Google Scholar
Levitt, G., ‘On the cost of generating an equivalence relation’, Ergod. Th. & Dynam. Sys. 15 (1995), 1173–1181.Google Scholar
Lovász, L., Large Networks and Graph Limits (Colloquium Publications, American Mathematical Society, 2012).Google Scholar
Lusin, N., Leçons sur les ensembles analytiques et leurs applications (Chelsea Publishing Co., New York, 1972), Réimpression de l’edition de 1930.Google Scholar
Lyons, R. and Nazarov, F., ‘Perfect matchings as IID factors on non-amenable groups’, European J. Combin. 32 (2011), 1115–1125.Google Scholar
Marks, A., ‘A determinacy approach to Borel combinatorics’, J. Amer. Math. Soc. 29 (2016), 579–600.Google Scholar
McDiarmid, C., ‘Concentration for independent permutations’, Combin. Probab. Comput. 11 (2002), 163–178.Google Scholar
Nguyen, H. N. and Onak, K., ‘Constant-time approximation algorithms via local improvements’, in49th Annual IEEE Symposium on Foundations of Computer Science (IEEE Computer Society, 2008), 327–336.Google Scholar
Petersen, J., ‘Die Theorie der regulären Graphs’, Acta Math. 15 (1891), 193–220.Google Scholar
Shalom, Y., Measurable Group Theory, European Congress of Mathematics (European Mathematical Society, Zürich, 2005), 391–423.Google Scholar
Stiebitz, M., Scheide, D., Toft, B. and Favrholdt, L. M., Graph Edge Coloring, Wiley Series in Discrete Mathematics and Optimization (John Wiley & Sons, Inc., Hoboken, NJ, 2012).Google Scholar
Tutte, W. T., ‘The factorization of linear graphs’, J. Lond. Math. Soc. (2) 22 (1947), 107–111.CrossRefGoogle Scholar
Vizing, V. G., ‘On an estimate of the chromatic class of a p-graph’, Diskret. Anal. 3 (1964), 25–30.Google Scholar