Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ruiz-Medina, María Dolores
and
Crujeiras, Rosa María
2011.
Minimum Contrast Parameter Estimation for Fractal Random Fields Based on the Wavelet Periodogram.
Communications in Statistics - Theory and Methods,
Vol. 40,
Issue. 19-20,
p.
3599.
Crujeiras, Rosa M.
and
Ruiz-Medina, María-Dolores
2011.
Recent Advances in Functional Data Analysis and Related Topics.
p.
63.
Sakhno, Lyudmyla
2012.
Minimum contrast estimation of stationary processes based on the squared periodogram∗.
Lithuanian Mathematical Journal,
Vol. 52,
Issue. 4,
p.
400.
Malyarenko, Anatoliy
2013.
Invariant Random Fields on Spaces with a Group Action.
p.
9.
Ruiz-Medina, M
Ruiz-Medina, M
Crujeiras, Rosa Maria
and
Crujeiras, Rosa Maria
2013.
A central limit result in the wavelet domain for minimum contrast estimation of fractal random fields.
Теория вероятностей и ее применения,
Vol. 58,
Issue. 3,
p.
550.
Frías, M. P.
Ruiz-Medina, M. D.
and
Anh, V. V.
2013.
Wavelet-Based Estimation of Anisotropic Spatiotemporal Long-Range Dependence.
Stochastic Analysis and Applications,
Vol. 31,
Issue. 3,
p.
359.
Anh, V. V.
Leonenko, N. N.
and
Ruiz-Medina, M. D.
2013.
Macroscaling Limit Theorems for Filtered Spatiotemporal Random Fields.
Stochastic Analysis and Applications,
Vol. 31,
Issue. 3,
p.
460.
Ivanov, Alexander V.
Leonenko, Nikolai
Ruiz-Medina, María D.
and
Savich, Irina N.
2013.
Limit theorems for weighted nonlinear transformations of Gaussian stationary processes with singular spectra.
The Annals of Probability,
Vol. 41,
Issue. 2,
Sakhno, Lyudmyla
2014.
Modern Stochastics and Applications.
Vol. 90,
Issue. ,
p.
319.
Ruiz-Medina, M. D.
and
Crujeiras, R. M.
2014.
A Central Limit Result in the Wavelet Domain for Minimum Contrast Estimation of Fractal Random Fields.
Theory of Probability & Its Applications,
Vol. 58,
Issue. 3,
p.
458.
Avram, Florin
Leonenko, Nikolai
and
Sakhno, Ludmila
2015.
Limit theorems for additive functionals of stationary fields, under integrability assumptions on the higher order spectral densities.
Stochastic Processes and their Applications,
Vol. 125,
Issue. 4,
p.
1629.
Ivanov, A.V.
Leonenko, N.N.
Ruiz-Medina, M.D.
and
Zhurakovsky, B.M.
2015.
Estimation of harmonic component in regression with cyclically dependent errors.
Statistics,
Vol. 49,
Issue. 1,
p.
156.
Ginovyan, M. S.
and
Sahakyan, A. A.
2016.
On the robustness to small trends of parameter estimation for continuous-time stationary models with memory.
Journal of Contemporary Mathematical Analysis,
Vol. 51,
Issue. 5,
p.
232.
Bai, Shuyang
Ginovyan, Mamikon S.
and
Taqqu, Murad S.
2016.
Limit theorems for quadratic forms of Lévy-driven continuous-time linear processes.
Stochastic Processes and their Applications,
Vol. 126,
Issue. 4,
p.
1036.
Alomari, Huda Mohammed
Frías, M. Pilar
Leonenko, Nikolai N.
Ruiz-Medina, María D.
Sakhno, Lyudmyla
and
Torres, Antoni
2017.
Asymptotic properties of parameter estimates for random fields with tapered data.
Electronic Journal of Statistics,
Vol. 11,
Issue. 2,
Ginovyan, M. S.
and
Sahakyan, A. A.
2019.
Limit Theorems for Tapered Toeplitz Quadratic Functionals of Continuous-time Gaussian Stationary Processes.
Journal of Contemporary Mathematical Analysis (Armenian Academy of Sciences),
Vol. 54,
Issue. 4,
p.
222.
Ginovyan, Mamikon S.
2020.
Parameter Estimation for Lévy-Driven Continuous-Time Linear Models with Tapered Data.
Acta Applicandae Mathematicae,
Vol. 169,
Issue. 1,
p.
79.
Olenko, Andriy
and
Vaskovych, Volodymyr
2020.
Non-central limit theorems for functionals of random fields on hypersurfaces.
ESAIM: Probability and Statistics,
Vol. 24,
Issue. ,
p.
315.
Blazhievska, Irina
and
Zaiats, Vladimir
2020.
Estimation of impulse response functions in two-output systems.
Communications in Statistics - Theory and Methods,
Vol. 49,
Issue. 2,
p.
257.
Ivanov, A. V.
Leonenko, N. N.
and
Orlovskyi, I. V.
2020.
On the Whittle estimator for linear random noise spectral density parameter in continuous-time nonlinear regression models.
Statistical Inference for Stochastic Processes,
Vol. 23,
Issue. 1,
p.
129.
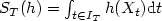 or for quadratic forms $Q_T(h)=\int_{t,s \in I_T} \hat{b}(t-s) h (X_t, X_s) {\rm d}s {\rm d}t$
or for quadratic forms $Q_T(h)=\int_{t,s \in I_T} \hat{b}(t-s) h (X_t, X_s) {\rm d}s {\rm d}t$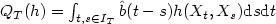 , where Xt is a stationary
process. A particularly important case is that of Appell
polynomials h(Xt) = Pm(Xt), h(Xt,Xs) = Pm,n (Xt,Xs), since the “Appell expansion rank" determines typically the
type of central limit theorem satisfied by the functionals
ST(h), QT(h).
We review and extend here to multidimensional
indices, along lines conjectured in [F. Avram and M.S. Taqqu, Lect. Notes Statist.187 (2006) 259–286], a functional
analysis approach to this problem proposed by [Avram and Brown, Proc. Amer.
Math. Soc.107 (1989) 687–695] based on the method of cumulants and on integrability
assumptions in the spectral domain; several applications are
presented as well.
, where Xt is a stationary
process. A particularly important case is that of Appell
polynomials h(Xt) = Pm(Xt), h(Xt,Xs) = Pm,n (Xt,Xs), since the “Appell expansion rank" determines typically the
type of central limit theorem satisfied by the functionals
ST(h), QT(h).
We review and extend here to multidimensional
indices, along lines conjectured in [F. Avram and M.S. Taqqu, Lect. Notes Statist.187 (2006) 259–286], a functional
analysis approach to this problem proposed by [Avram and Brown, Proc. Amer.
Math. Soc.107 (1989) 687–695] based on the method of cumulants and on integrability
assumptions in the spectral domain; several applications are
presented as well.




