Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-07-03T07:10:36.592Z Has data issue: false hasContentIssue false
  • English
  • Français

Renormalization for Lorenz maps of monotone combinatorial types

Published online by Cambridge University Press:  22 May 2017

DENIS GAIDASHEV
DENIS GAIDASHEV*
Affiliation:
Department of Mathematics, Uppsala University, Uppsala, Sweden email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Lorenz maps are maps of the unit interval with one critical point of order 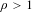$\unicode[STIX]{x1D70C}>1$ and a discontinuity at that point. They appear as return maps of sections of the geometric Lorenz flow. We construct real a priori bounds for renormalizable Lorenz maps with certain monotone combinatorics and a sufficiently flat critical point, and use these bounds to show existence of periodic points of renormalization, as well as existence of Cantor attractors for dynamics of infinitely renormalizable Lorenz maps.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 1 , January 2019 , pp. 132 - 158
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Collet, P., Coullet, P. and Tresser, C.. Scenarios under constraint. J. Phys. Lett. 46(4) (1985), 143–147.Google Scholar
Gaidashev, D. and Winckler, B.. Existence of a Lorenz renormalization fixed point of an arbitrary critical order. Nonlinearity 25 (2012), 1819.Google Scholar
Gambaudo, J.-M. and Martens, M.. Algebraic topology for minimal Cantor sets. Ann. Henri Poincaré 7(3) (2006), 423–446.Google Scholar
Granas, A. and Dugundji, J.. Fixed Point Theory (Springer Monographs in Mathematics) . Springer, New York, 2003.Google Scholar
Guckenheimer, J. and Williams, R. F.. Structural stability of the Lorenz attractors. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 59–72.Google Scholar
Hubbard, J. H. and Sparrow, C. T.. The classification of topologically expansive Lorenz maps. Comm. Pure Appl. Math. XLIII (1990), 431–443.Google Scholar
Lorenz, E. N.. Deterministic non-periodic flow. J. Atmos. Sci. 20 (1963), 130–141.Google Scholar
Martens, M. and de Melo, W.. Universal models for Lorenz maps. Ergod. Th. & Dynam. Sys. 21(3) (2001), 833–860.Google Scholar
Martens, M. and Winckler, B.. On the hyperbolicity of Lorenz renormalization. Comm. Math. Phys. 325(1) (2014), 185–257.Google Scholar
de Melo, W. and van Strien, S.. One-dimensional Dynamics (Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 25) . Springer, Berlin, 1993.Google Scholar
Misiurewicz, M.. Absolutely continuous measures for certain maps of an interval. Publ. Math. Inst. Hautes Études Sci. 53 (1981), 17–51.Google Scholar
Williams, R. F.. The structure of the Lorenz attractors. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 73–79.Google Scholar
Winckler, B.. A renormalization fixed point for Lorenz maps. Nonlinearity 23(6) (2010), 1291–1303.Google Scholar