Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-07-01T00:39:36.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Renewal-type limit theorem for the Gauss map and continued fractions

Published online by Cambridge University Press:  01 April 2008

YAKOV G. SINAI  and
CORINNA ULCIGRAI
YAKOV G. SINAI
Affiliation:
Mathematics Department, Princeton University, Fine Hall, Washington Road, Princeton, NJ 08544-1000, USA (email: [email protected], [email protected])
CORINNA ULCIGRAI
Affiliation:
Mathematics Department, Princeton University, Fine Hall, Washington Road, Princeton, NJ 08544-1000, USA (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

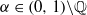In this paper we prove a renewal-type limit theorem. Given and R>0, let qnR be the first denominator of the convergents of α which exceeds R. The main result in the paper is that the ratio qnR/R has a limiting distribution as R tends to infinity. The existence of the limiting distribution uses mixing of a special flow over the natural extension of the Gauss map.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 2: William Parry Memorial Volume , April 2008 , pp. 643 - 655
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bourgain, J. and Sinai, Ya. G.. Limiting behaviour of large Frobenius numbers. Uspekhi. Mat. Nauk. 72(4) (2007), 77–90.Google Scholar
[2]Cornfeld, I. P., Fomin, S. V. and Sinai, Ya. G.. Ergodic Theory. Springer, Berlin, 1980.Google Scholar
[3]Dinaburg, E. I. and Sinai, Ya. G.. Statistics of solutions of the integral equation ax−by=±1. Funct. Anal. Appl. 24(3) (1990), 1–8.Google Scholar
[4]Kesseböhmer, M. and Slassi, M.. A distributional limit law for continued fraction digit sums. Math. Nach. to appear. arXiv:math.NT/0509559, 2007.Google Scholar
[5]Khinchin, A. Ya.. Continued Fractions. The University of Chicago Press, Chicago, IL, 1935.Google Scholar
[6]Sinai, Ya. G.. Topics in Ergodic Theory. Princeton University Press, Princeton, NJ, 1994.CrossRefGoogle Scholar
[7]Sinai, Ya. G. and Ulcigrai, C.. A limit theorem for Birkhoff sums of non-integrable functions over rotations. Probabilistic and Geometric Structures in Dynamics (Contemporary Mathematics). Eds. K. Burns, D. Dolgopyat and Ya. Pesin. American Mathematical Society, Providence, RI, 2008.Google Scholar
[8]Arnold, V. I.. Weak asymtotics for the number of solutions of Diophantine problems. Funct. Anal. Appl. 33(4) (1999), 292–293.CrossRefGoogle Scholar