Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T03:56:19.092Z Has data issue: false hasContentIssue false
  • English
  • Français

Global dynamical properties of Euler and backward Euler

Published online by Cambridge University Press:  19 September 2008

Kevin Hockett
Kevin Hockett
Affiliation:
Department of Mathematics, The George Washington University, Washington, DC 20052, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the global dynamics of both the Euler and backward Euler algorithms as applied to polynomial vector fields on the Riemann sphere 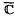= ℂ ∪ {∞}. The geometry and dynamics of solutions at infinity is seen to play an important role in organizing the global dynamics of the flow, and we show how to modify both algorithms to account for this structure, thereby obtaining global approximations to the flow.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 13 , Issue 4 , December 1993 , pp. 675 - 696
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlfors, L.. Complex Analysis. 3rd edn.McGraw-Hill, New York, 1979.Google Scholar
Benzinger, H.. Plane autonomous systems with rational vector fields. Trans. Amer. Math. Soc. 326 (1991),CrossRefGoogle Scholar
Blanchard, P.. Complex analytic dynamics on the Riemann sphere. Bull. Amer. Math. Soc. (New Series). 11 (1992), 85–141.CrossRefGoogle Scholar
Broomhead, D. S. & Iserles, A. (eds). The Dynamics of Numerics and the Numerics of Dynamics. Oxford University Press, Oxford, 1992.Google Scholar
Curry, J., Garnett, L. & Sullivan, D.. On the iteration of a rational function: computer experiments with Newton's method. Commun. Math. Phys. 91 (1983), 267–277.CrossRefGoogle Scholar
Devaney, R.. Singularities in classical mechanical systems. Ergodic Theory and Dynamical Systems I, Proceedings, Special Year, Maryland, 1979–80, ed. Katok, A.. Birkhauser, Boston, 1981.Google Scholar
Devaney, R.. Blowing up singularities in classical mechanical systems. Amer. Math. Monthly. 89 (1982), 535–552.CrossRefGoogle Scholar
Devaney, R.. An Introduction to Chaotic Dynamical Systems. Benjamin-Cummings, Menlo Park, 1986.Google Scholar
Guckenheimer, J. & Holmes, P.. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York, 1986.Google Scholar
Henrici, P.. Discrete Variable Methods in Ordinary Differential Equations. Wiley, New York, 1962.Google Scholar
Hockett, K.. Chaotic numerics from an integrable Hamiltonian system. Proc. Amer. Math. Soc. 108 (1990), 271–281.CrossRefGoogle Scholar
Hockett, K.. Numerical dynamics of ordinary differential equations with singularity. Proc. Amer. Math. Soc. 117 (1993), 369–379.CrossRefGoogle Scholar
Hurley, M.. Multiple attractors in Newton's method. Ergod. Th. & Dynam. Sys. 6, (1986), 561–569.CrossRefGoogle Scholar
Kim, M. & Sutherland, S.. Families of parallel root-finding algorithms. SUNY Stony Brook Institute for Mathematical Sciences. Preprint # 1991/5.Google Scholar
Kloeden, P. E. & Lorenz, J.. Stable attracting sets in dynamical systems and in their one-step discretizations. SIAMJ. Numer. Anal. 23 (1986), 986–995.CrossRefGoogle Scholar
Kloeden, P. E. & Lorenz, J.. A note on multistep methods and attracting sets of dynamical systems. Numer. Math. 56 (1990), 667–673.CrossRefGoogle Scholar
Lehto, O.. Univalent Functions and Teichmiiller Spaces. Springer, New York, 1991.Google Scholar
Milnor, J.. Dynamics in one complex variable: introductory lectures. SUNY Stony Brook Institute for Mathematical Sciences, Preprint # 1990/5.Google Scholar
Nevanlinna, R. & Paatero, V.. Introduction to Complex Analysis. Chelsea Publishing Co., New York, 1982.Google Scholar
Parthasarathy, T.. On Global Univalence Theorems. Springer Lecture Notes in Mathematics 977. Springer, New York, 1983.CrossRefGoogle Scholar
Smale, S.. On the efficiency of algorithms of analysis. Bull. Amer. Math. Soc. 13 (1985), 87–121.CrossRefGoogle Scholar
Sutherland, S.. Finding roots of complex polynomials with Newton's method. Preprint (1989), Institute for Mathematical Sciences, SUNY Stony Brook.Google Scholar