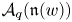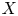1. Introduction
A cluster algebra and its non-commutative version quantum cluster algebra, were introduced by Berenstein, Fomin and Zelevinsky [Reference Fomin and ZelevinskyFZ02, Reference Berenstein and ZelevinskyBZ05] in an attempt to provide an algebraic and combinatorial framework for investigating the upper global basis of the quantum group.
The quantum cluster algebra ![]() $\mathscr {A}_q$ is a non-commutative
$\mathscr {A}_q$ is a non-commutative ![]() $\mathbb {Z}\mspace {1mu}[q^{\pm 1/2}]$-subalgebra in the skew field
$\mathbb {Z}\mspace {1mu}[q^{\pm 1/2}]$-subalgebra in the skew field ![]() $\mathbb {Q}(q^{1/2})(X_i)_{i \in \mathsf {K}}$ generated by the cluster variables, which are obtained from the initial cluster
$\mathbb {Q}(q^{1/2})(X_i)_{i \in \mathsf {K}}$ generated by the cluster variables, which are obtained from the initial cluster ![]() $\{ X_{i} \}_{i \in \mathsf {K}}$ via the sequences of procedures, called mutations. Even though mutations involve non-trivial fractions,
$\{ X_{i} \}_{i \in \mathsf {K}}$ via the sequences of procedures, called mutations. Even though mutations involve non-trivial fractions, ![]() $\mathscr {A}_q$ is still contained in
$\mathscr {A}_q$ is still contained in ![]() $\mathbb {Z}\mspace {1mu}[q^{\pm 1/2}][X_i^{\pm 1}]_{i \in \mathsf {K}}$ with amazing reductions of fractions which is referred to as the quantum Laurent phenomenon [Reference Berenstein and ZelevinskyBZ05]. The famous conjecture, which is not completely proved yet at this moment, is the quantum Laurent positivity conjecture which asserts that every cluster variable is an element in
$\mathbb {Z}\mspace {1mu}[q^{\pm 1/2}][X_i^{\pm 1}]_{i \in \mathsf {K}}$ with amazing reductions of fractions which is referred to as the quantum Laurent phenomenon [Reference Berenstein and ZelevinskyBZ05]. The famous conjecture, which is not completely proved yet at this moment, is the quantum Laurent positivity conjecture which asserts that every cluster variable is an element in ![]() $\mathbb {Z}\mspace {1mu}_{\geqslant 0}[q^{\pm 1/2}][\mathsf {X}_i^{\pm 1}]_{i \in \mathsf {K}}$ for any cluster
$\mathbb {Z}\mspace {1mu}_{\geqslant 0}[q^{\pm 1/2}][\mathsf {X}_i^{\pm 1}]_{i \in \mathsf {K}}$ for any cluster ![]() $\{\mathsf {X}_i\}_{i \in \mathsf {K}}$. Note that the conjecture is proved in [Reference DavisonDav18] (see also [Reference Lee and SchifflerLS15, Reference Gross, Hacking, Keel and KontsevichGHKK18]) when
$\{\mathsf {X}_i\}_{i \in \mathsf {K}}$. Note that the conjecture is proved in [Reference DavisonDav18] (see also [Reference Lee and SchifflerLS15, Reference Gross, Hacking, Keel and KontsevichGHKK18]) when ![]() $\mathscr {A}_q$ is of skew-symmetric type and is widely open when it is of non-skew-symmetric type.
$\mathscr {A}_q$ is of skew-symmetric type and is widely open when it is of non-skew-symmetric type.
The notion of monoidal categorification of (quantum) cluster algebra was introduced by Hernandez and Leclerc in [Reference Hernandez and LeclercHL10] (see also [Reference Kang, Kashiwara, Kim and OhKKKO18]) as the categorical framework for proving the conjecture as follows: a monoidal category ![]() $\mathcal {C}$ with an autofunctor
$\mathcal {C}$ with an autofunctor ![]() $q$ is a monoidal categorification of
$q$ is a monoidal categorification of ![]() $\mathscr {A}_q$, if (a)
$\mathscr {A}_q$, if (a) ![]() $\mathbb {A} \otimes _{\mathbb {Z}\mspace {1mu}[q^{\pm 1}]} K(\mathcal {C})$
$\mathbb {A} \otimes _{\mathbb {Z}\mspace {1mu}[q^{\pm 1}]} K(\mathcal {C})$ ![]() $(\mathbb {A} \mathbin {:=}\mathbb {Z}\mspace {1mu}[q^{\pm 1/2}])$ is isomorphic to
$(\mathbb {A} \mathbin {:=}\mathbb {Z}\mspace {1mu}[q^{\pm 1/2}])$ is isomorphic to ![]() $\mathscr {A}_q$ and (b) the cluster monomials of
$\mathscr {A}_q$ and (b) the cluster monomials of ![]() $\mathscr {A}_q$ are the classes of real simple objects of
$\mathscr {A}_q$ are the classes of real simple objects of ![]() $\mathcal {C}$. Once
$\mathcal {C}$. Once ![]() $\mathcal {C}$ is a monoidal categorification of
$\mathcal {C}$ is a monoidal categorification of ![]() $\mathscr {A}_q$, then the conjecture for
$\mathscr {A}_q$, then the conjecture for ![]() $\mathscr {A}_q$ follows since it can be interpreted as the existence of a Jordan–Hölder series of an object. In [Reference Kang, Kashiwara, Kim and OhKKKO18], it is proved that the category
$\mathscr {A}_q$ follows since it can be interpreted as the existence of a Jordan–Hölder series of an object. In [Reference Kang, Kashiwara, Kim and OhKKKO18], it is proved that the category ![]() $\mathscr {C}_w$ over symmetric quiver Hecke algebra
$\mathscr {C}_w$ over symmetric quiver Hecke algebra ![]() $\mathsf {R}$ is a monoidal categorification of the quantum unipotent coordinate ring
$\mathsf {R}$ is a monoidal categorification of the quantum unipotent coordinate ring ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ associated with an element
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ associated with an element ![]() $w$ of the Weyl group
$w$ of the Weyl group ![]() $\mathsf {W}$ by using the
$\mathsf {W}$ by using the ![]() $\mathbb {Z}\mspace {1mu}$-invariant
$\mathbb {Z}\mspace {1mu}$-invariant ![]() $\Lambda (M,N)$ of a pair of simple objects
$\Lambda (M,N)$ of a pair of simple objects ![]() $M,N \in \mathscr {C}_w$.
$M,N \in \mathscr {C}_w$.
For non-symmetric cases, the monoidal categorification is still out of reach. We know that ![]() $\mathscr {C}_w$ categorifies
$\mathscr {C}_w$ categorifies ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ as an algebra [Reference Khovanov and LaudaKL09, Reference Khovanov and LaudaKL11, Reference RouquierRou08, Reference KimuraKim12] and
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ as an algebra [Reference Khovanov and LaudaKL09, Reference Khovanov and LaudaKL11, Reference RouquierRou08, Reference KimuraKim12] and ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ has a quantum cluster algebra structure [Reference Geiss, Leclerc and SchröerGLS13a, Reference Goodearl and YakimovGY17] in every symmetrizable case. The quantum cluster algebra structure is skew-symmetric if the corresponding generalized Cartan matrix is symmetric. However, we cannot prove that
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ has a quantum cluster algebra structure [Reference Geiss, Leclerc and SchröerGLS13a, Reference Goodearl and YakimovGY17] in every symmetrizable case. The quantum cluster algebra structure is skew-symmetric if the corresponding generalized Cartan matrix is symmetric. However, we cannot prove that ![]() $\mathscr {C}_w$ is a monoidal categorification of
$\mathscr {C}_w$ is a monoidal categorification of ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ in non-symmetric cases due to the obstacle that we do not know whether every simple module
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ in non-symmetric cases due to the obstacle that we do not know whether every simple module ![]() $M \in \mathscr {C}_w$ admits an affinization [Reference Kashiwara and ParkKP18] or not. Note that the existence of affinizations guarantees that one can define
$M \in \mathscr {C}_w$ admits an affinization [Reference Kashiwara and ParkKP18] or not. Note that the existence of affinizations guarantees that one can define ![]() $R$-matrices and the
$R$-matrices and the ![]() $\mathbb {Z}\mspace {1mu}$-invariant
$\mathbb {Z}\mspace {1mu}$-invariant ![]() $\Lambda (M,N)$.
$\Lambda (M,N)$.
In this paper, we study the quantum Laurent positivity for ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ of not necessarily symmetric type in the view point of the monoidal categorification. More precisely, we show that the basis of
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ of not necessarily symmetric type in the view point of the monoidal categorification. More precisely, we show that the basis of ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ corresponding to the simple modules in
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ corresponding to the simple modules in ![]() $\mathscr {C}_w$ exhibits a quantum Laurent positivity phenomenon with respect to any quasi-Laurent family, which is a central notion we introduce in this paper and plays the similar role of a cluster in the quantum cluster algebra theory.
$\mathscr {C}_w$ exhibits a quantum Laurent positivity phenomenon with respect to any quasi-Laurent family, which is a central notion we introduce in this paper and plays the similar role of a cluster in the quantum cluster algebra theory.
The quasi-Laurent family (respectively, Laurent family) ![]() $\mathcal {M}=\{ M_j \}_{j \in J}$ consists of mutually commuting affreal simple modules in
$\mathcal {M}=\{ M_j \}_{j \in J}$ consists of mutually commuting affreal simple modules in ![]() $\mathscr {C}_w$ satisfying additional conditions (Definition 3.2). Among others, the most important condition is that if a simple module
$\mathscr {C}_w$ satisfying additional conditions (Definition 3.2). Among others, the most important condition is that if a simple module ![]() $X$ commutes with all
$X$ commutes with all ![]() $M_j$, then there are monomials (i.e. convolution products)
$M_j$, then there are monomials (i.e. convolution products) ![]() $\mathcal {M}(\boldsymbol a)$ and
$\mathcal {M}(\boldsymbol a)$ and ![]() $\mathcal {M}(\boldsymbol b)$ in
$\mathcal {M}(\boldsymbol b)$ in ![]() $\{M_j\}_{j\in J}$ such that
$\{M_j\}_{j\in J}$ such that ![]() $X \circ \mathcal {M}(\boldsymbol a)$ is isomorphic to
$X \circ \mathcal {M}(\boldsymbol a)$ is isomorphic to ![]() $\mathcal {M}(\boldsymbol b)$. We say the family
$\mathcal {M}(\boldsymbol b)$. We say the family ![]() $\mathcal {M}$ is Laurent if
$\mathcal {M}$ is Laurent if ![]() $\mathcal {M}$ is maximal in the sense that, if a simple module
$\mathcal {M}$ is maximal in the sense that, if a simple module ![]() $X$ commutes with all
$X$ commutes with all ![]() $M_j$, then
$M_j$, then ![]() $X$ is isomorphic to a monomial
$X$ is isomorphic to a monomial ![]() $\mathcal {M}(\boldsymbol b)$ in
$\mathcal {M}(\boldsymbol b)$ in ![]() $\{M_j\}_{j\in J}$.
$\{M_j\}_{j\in J}$.
The main results of this paper are the following.
(A) We show that if
 $\mathcal {M}$ is a quasi-Laurent family in
$\mathcal {M}$ is a quasi-Laurent family in  $\mathscr {C}_w$, then the class
$\mathscr {C}_w$, then the class  $[X]$ in the Grothendieck ring
$[X]$ in the Grothendieck ring  $K(\mathscr {C}_w)$ of any simple object
$K(\mathscr {C}_w)$ of any simple object  $X$ in
$X$ in  $\mathscr {C}_w$ can be written as a Laurent polynomial in
$\mathscr {C}_w$ can be written as a Laurent polynomial in  $\{ [M_j] \}_{j \in J}$ whose coefficients belong to
$\{ [M_j] \}_{j \in J}$ whose coefficients belong to  $\mathbb {Z}\mspace {1mu}_{\ge 0}[q^{\pm 1}]$ (Proposition 3.6).
$\mathbb {Z}\mspace {1mu}_{\ge 0}[q^{\pm 1}]$ (Proposition 3.6).(B) If
 $\mathcal {M}$ is a monoidal seed in
$\mathcal {M}$ is a monoidal seed in  $\mathscr {C}_w$, then
$\mathscr {C}_w$, then  $\mathcal {M}$ is a Laurent family.
$\mathcal {M}$ is a Laurent family.(C) In particular, for any reduced sequence
 ${\boldsymbol{i}}$ of
${\boldsymbol{i}}$ of  $w$, we show that the family
$w$, we show that the family  $\mathcal {M}^{\boldsymbol{i}} \mathbin {:=} \{ M(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k}) \}$ is a Laurent family and, hence, any class
$\mathcal {M}^{\boldsymbol{i}} \mathbin {:=} \{ M(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k}) \}$ is a Laurent family and, hence, any class  $[X]$ of a module
$[X]$ of a module  $X$ in
$X$ in  $\mathscr {C}_w$ can be written as a Laurent polynomial in the unipotent quantum minors
$\mathscr {C}_w$ can be written as a Laurent polynomial in the unipotent quantum minors  $D(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k})$ with coefficients in
$D(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k})$ with coefficients in  $\mathbb {Z}\mspace {1mu}_{\ge 0}[q^{\pm 1}]$. Note that
$\mathbb {Z}\mspace {1mu}_{\ge 0}[q^{\pm 1}]$. Note that  $D(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k})=[M(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k}) ]$ and we call
$D(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k})=[M(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k}) ]$ and we call  $\{D(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k})\}$ the GLS seed associated with
$\{D(w_{\leqslant k}^{\boldsymbol {i}} \varpi _{i_k},\varpi _{i_k})\}$ the GLS seed associated with  ${\boldsymbol {i}}$ (Proposition 4.5).
${\boldsymbol {i}}$ (Proposition 4.5).(D) We show that if
 $\mathcal {M}$ is a quasi-Laurent family, then the class
$\mathcal {M}$ is a quasi-Laurent family, then the class  $[X]$ of a simple module
$[X]$ of a simple module  $X$ in
$X$ in  $\mathscr {C}_w$ is pointed and copointed with respect to the partial order
$\mathscr {C}_w$ is pointed and copointed with respect to the partial order  $\preccurlyeq _\mathcal {M}$. That is, the set of degrees of the monomials appearing in the Laurent expansion of
$\preccurlyeq _\mathcal {M}$. That is, the set of degrees of the monomials appearing in the Laurent expansion of  $[X]$ with respect to
$[X]$ with respect to  $\mathcal {M}$ has a unique maximal element and a unique minimal element with respect to
$\mathcal {M}$ has a unique maximal element and a unique minimal element with respect to  $\preccurlyeq _\mathcal {M}$. We define vectors
$\preccurlyeq _\mathcal {M}$. We define vectors  $\mathbf {g}_\mathcal {M}^R(X)$ and
$\mathbf {g}_\mathcal {M}^R(X)$ and  $\mathbf {g}_\mathcal {M}^L(X) \in \mathbb {Z}\mspace {1mu}^{\oplus J}$ as the maximal and the minimal element, respectively.
$\mathbf {g}_\mathcal {M}^L(X) \in \mathbb {Z}\mspace {1mu}^{\oplus J}$ as the maximal and the minimal element, respectively.(E) Each quasi-Laurent family
 $\mathcal {M}$ also induces new
$\mathcal {M}$ also induces new  $\mathbb {Z}\mspace {1mu}$-values
$\mathbb {Z}\mspace {1mu}$-values  ${\mathrm G}_\mathcal {M}^R(X,Y)$ and
${\mathrm G}_\mathcal {M}^R(X,Y)$ and  ${\mathrm G}_\mathcal {M}^L(X,Y)$ for any pair of simple modules
${\mathrm G}_\mathcal {M}^L(X,Y)$ for any pair of simple modules  $X$ and
$X$ and  $Y$ which coincides with
$Y$ which coincides with  $\Lambda (X,Y)$ provided
$\Lambda (X,Y)$ provided  $X,Y$ commutes and one of them is affreal.
$X,Y$ commutes and one of them is affreal.
To the best of the authors’ knowledge, the positivity result in part (C) is new. We can understand result (A) that a quasi-Laurent family is a generalization of a cluster in the categorical view point, and that the positivity conjecture can be extended to elements corresponding to simple modules in all skew-symmetrizable types.
In [Reference Fomin and ZelevinskyFZ07, Reference QinQin17], Fomin-Zelevinsky and Qin defined a pointed (respectively, copointed) element ![]() $\mathbf {x}$ in a cluster algebra and its degree
$\mathbf {x}$ in a cluster algebra and its degree ![]() $\mathbf {deg}_{\mathcal {S}}(\mathbf {x}) \in \mathbb {Z}\mspace {1mu}^{\oplus \mathsf {K}}$ (respectively, codegree
$\mathbf {deg}_{\mathcal {S}}(\mathbf {x}) \in \mathbb {Z}\mspace {1mu}^{\oplus \mathsf {K}}$ (respectively, codegree ![]() $\mathbf {codeg}_{\mathcal {S}}(\mathbf {x}) \in \mathbb {Z}\mspace {1mu}^{\oplus \mathsf {K}}$) depending on the choice of a seed
$\mathbf {codeg}_{\mathcal {S}}(\mathbf {x}) \in \mathbb {Z}\mspace {1mu}^{\oplus \mathsf {K}}$) depending on the choice of a seed ![]() $\mathcal {S}$ (see also [Reference QinQin20] for codegree and [Reference TranTra11] for degree elements in a quantum cluster algebra). With a fixed choice of a seed, it is proved in [Reference TranTra11] that every cluster monomial is pointed, and in [Reference Derksen, Weyman and ZelevinskyDWZ10, Reference Gross, Hacking, Keel and KontsevichGHKK18] that cluster monomials are determined by their degrees.
$\mathcal {S}$ (see also [Reference QinQin20] for codegree and [Reference TranTra11] for degree elements in a quantum cluster algebra). With a fixed choice of a seed, it is proved in [Reference TranTra11] that every cluster monomial is pointed, and in [Reference Derksen, Weyman and ZelevinskyDWZ10, Reference Gross, Hacking, Keel and KontsevichGHKK18] that cluster monomials are determined by their degrees.
For a given quasi-Laurent family ![]() $\mathcal {M}$ and a simple module
$\mathcal {M}$ and a simple module ![]() $X \in \mathscr {C}_w$, we define vectors
$X \in \mathscr {C}_w$, we define vectors ![]() $\mathbf {g}_\mathcal {M}^R(X),\mathbf {g}_\mathcal {M}^L(X) \in \mathbb {Z}\mspace {1mu}^{\oplus J }$ in Definition 3.7 by using the
$\mathbf {g}_\mathcal {M}^R(X),\mathbf {g}_\mathcal {M}^L(X) \in \mathbb {Z}\mspace {1mu}^{\oplus J }$ in Definition 3.7 by using the ![]() $\mathbb {Z}\mspace {1mu}^{\oplus J}_{\geqslant 0}$-vectors in Lemma 3.3 and guaranteeing its well-definedness in Lemma 3.1. We then prove that, for every simple module
$\mathbb {Z}\mspace {1mu}^{\oplus J}_{\geqslant 0}$-vectors in Lemma 3.3 and guaranteeing its well-definedness in Lemma 3.1. We then prove that, for every simple module ![]() $X \in \mathscr {C}_w$, the element
$X \in \mathscr {C}_w$, the element ![]() $[X]$ in
$[X]$ in ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ is (co)pointed with respect to the GLS seed
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ is (co)pointed with respect to the GLS seed ![]() $\mathcal {S}^{\boldsymbol {i}}$ and that
$\mathcal {S}^{\boldsymbol {i}}$ and that ![]() $\mathbf {g}_{\mathcal {M}^{{\boldsymbol {i}}}}^R(X)$ and
$\mathbf {g}_{\mathcal {M}^{{\boldsymbol {i}}}}^R(X)$ and ![]() $\mathbf {g}_{\mathcal {M}^{{\boldsymbol {i}}}}^L(X)$ coincide with
$\mathbf {g}_{\mathcal {M}^{{\boldsymbol {i}}}}^L(X)$ coincide with ![]() $\mathbf {deg}_{\mathcal {S}^{\boldsymbol {i}}}([X])$ and
$\mathbf {deg}_{\mathcal {S}^{\boldsymbol {i}}}([X])$ and ![]() $\mathbf {codeg}_{\mathcal {S}^{\boldsymbol {i}}}([X])$, respectively.
$\mathbf {codeg}_{\mathcal {S}^{\boldsymbol {i}}}([X])$, respectively.
Utilizing the vectors ![]() $\mathbf {g}_\mathcal {M}^R(X)$ and
$\mathbf {g}_\mathcal {M}^R(X)$ and ![]() $\mathbf {g}_\mathcal {M}^L(X)$, we define skew-symmetric
$\mathbf {g}_\mathcal {M}^L(X)$, we define skew-symmetric ![]() $\mathbb {Z}\mspace {1mu}$-valued forms
$\mathbb {Z}\mspace {1mu}$-valued forms ![]() ${\mathrm G}_\mathcal {M}^R(-,-)$ and
${\mathrm G}_\mathcal {M}^R(-,-)$ and ![]() ${\mathrm G}_\mathcal {M}^L(-,-)$ on the pairs
${\mathrm G}_\mathcal {M}^L(-,-)$ on the pairs ![]() $(X,Y)$ of simple modules. Then we compare
$(X,Y)$ of simple modules. Then we compare ![]() ${\mathrm G}_\mathcal {M}^R(X,Y)$ and
${\mathrm G}_\mathcal {M}^R(X,Y)$ and ![]() ${\mathrm G}_\mathcal {M}^L(X,Y)$ with the
${\mathrm G}_\mathcal {M}^L(X,Y)$ with the ![]() $\mathbb {Z}\mspace {1mu}$-invariant
$\mathbb {Z}\mspace {1mu}$-invariant ![]() $\Lambda (X,Y)$ when the pair of simple module
$\Lambda (X,Y)$ when the pair of simple module ![]() $(X,Y)$ admits the
$(X,Y)$ admits the ![]() $\mathbb {Z}\mspace {1mu}$-invariant
$\mathbb {Z}\mspace {1mu}$-invariant ![]() $\Lambda (X,Y)$. It is proved in Proposition 5.3 that
$\Lambda (X,Y)$. It is proved in Proposition 5.3 that ![]() ${\mathrm G}_\mathcal {M}^R(X,Y)$ and
${\mathrm G}_\mathcal {M}^R(X,Y)$ and ![]() ${\mathrm G}_\mathcal {M}^L(X,Y)$ give lower bounds of
${\mathrm G}_\mathcal {M}^L(X,Y)$ give lower bounds of ![]() $\Lambda (X,Y)$, and in Proposition 5.4 that
$\Lambda (X,Y)$, and in Proposition 5.4 that ![]() ${\mathrm G}_\mathcal {M}^R(X,Y)={\mathrm G}_\mathcal {M}^L(X,Y)=\Lambda (X,Y)$ when
${\mathrm G}_\mathcal {M}^R(X,Y)={\mathrm G}_\mathcal {M}^L(X,Y)=\Lambda (X,Y)$ when ![]() $(X,Y)$ is a commuting pair. Here we would like to emphasize that (1)
$(X,Y)$ is a commuting pair. Here we would like to emphasize that (1) ![]() ${\mathrm G}_\mathcal {M}^R(X,Y)$ and
${\mathrm G}_\mathcal {M}^R(X,Y)$ and ![]() ${\mathrm G}_\mathcal {M}^L(X,Y)$ are defined even for pairs
${\mathrm G}_\mathcal {M}^L(X,Y)$ are defined even for pairs ![]() $(X,Y)$ we do not know whether they admit
$(X,Y)$ we do not know whether they admit ![]() $\Lambda (X,Y)$ or not, and (2) the
$\Lambda (X,Y)$ or not, and (2) the ![]() $\mathbb {Z}\mspace {1mu}$-values
$\mathbb {Z}\mspace {1mu}$-values ![]() ${\mathrm G}_\mathcal {M}^R(X,Y)$ and
${\mathrm G}_\mathcal {M}^R(X,Y)$ and ![]() ${\mathrm G}_\mathcal {M}^L(X,Y)$ do depend on the choice of
${\mathrm G}_\mathcal {M}^L(X,Y)$ do depend on the choice of ![]() $\mathcal {M}$ as (co)degree does on the one of seeds (Remark 5.5).
$\mathcal {M}$ as (co)degree does on the one of seeds (Remark 5.5).
This paper is organized as follows. In § 2, we give preliminaries. In § 3, we define the notions of quasi-Laurent and Laurent families, and investigate their properties. Then we define ![]() $\mathbf {g}_{\mathcal {M}}^R(X)$ and
$\mathbf {g}_{\mathcal {M}}^R(X)$ and ![]() $\mathbf {g}_{\mathcal {M}}^L(X)$, and prove that
$\mathbf {g}_{\mathcal {M}}^L(X)$, and prove that ![]() $\mathbf {g}_{\mathcal {M}}^R(X)$ and
$\mathbf {g}_{\mathcal {M}}^R(X)$ and ![]() $\mathbf {g}_{\mathcal {M}}^L(X)$ determine the isomorphism class of
$\mathbf {g}_{\mathcal {M}}^L(X)$ determine the isomorphism class of ![]() $X$. In § 4, we prove that
$X$. In § 4, we prove that ![]() $\mathcal {M}^{\boldsymbol {i}}$ is Laurent by studying PBW decomposition vectors of simple modules. In § 5, we define the skew-symmetric pairings on pairs of simple modules and investigate the relationships among the pairings and
$\mathcal {M}^{\boldsymbol {i}}$ is Laurent by studying PBW decomposition vectors of simple modules. In § 5, we define the skew-symmetric pairings on pairs of simple modules and investigate the relationships among the pairings and ![]() $\Lambda$-invariants.
$\Lambda$-invariants.
Convention Throughout this paper, we use the following convention.
(i) For a statement
 $\mathtt {P}$, we set
$\mathtt {P}$, we set  $\delta (\mathtt {P})$ to be
$\delta (\mathtt {P})$ to be  $1$ or
$1$ or  $0$ depending on whether
$0$ depending on whether  $\mathtt {P}$ is true or not. As a special case, we use the notation
$\mathtt {P}$ is true or not. As a special case, we use the notation  $\delta _{i,j} \mathbin {:=} \delta (i=j)$ (Kronecker's delta).
$\delta _{i,j} \mathbin {:=} \delta (i=j)$ (Kronecker's delta).(ii) For integers
 $a,b \in \mathbb {Z}\mspace {1mu}$, we set
We refer to the subset as an interval and understand it as an empty set if
$a,b \in \mathbb {Z}\mspace {1mu}$, we set
We refer to the subset as an interval and understand it as an empty set if \[ [a,b] \mathbin{:=} \{ x\in \mathbb{Z}\mspace{1mu} \; | \; a \leqslant x \leqslant b\}. \]
\[ [a,b] \mathbin{:=} \{ x\in \mathbb{Z}\mspace{1mu} \; | \; a \leqslant x \leqslant b\}. \]
 $a>b$.
$a>b$.(iii) Let
 $\mathbf {x}=(x_j )_{ j \in J }$ be a family parameterized by an index set
$\mathbf {x}=(x_j )_{ j \in J }$ be a family parameterized by an index set  $J$. Then for any
$J$. Then for any  $j \in J$, we set
$j \in J$, we set
 \[ (\mathbf{x})_j \mathbin{:=} x_j. \]
\[ (\mathbf{x})_j \mathbin{:=} x_j. \]
2. Preliminaries
In this preliminary section, we briefly review the basic material of this paper. We refer the reader to [Reference Berenstein and ZelevinskyBZ05, Reference Fomin and ZelevinskyFZ07, Reference Khovanov and LaudaKL09, Reference RouquierRou08, Reference KimuraKim12, Reference Geiss, Leclerc and SchröerGLS13a, Reference Kang, Kashiwara, Kim and OhKKKO18, Reference Goodearl and YakimovGY17, Reference Kimura and OyaKiOy21, Reference Kashiwara and ParkKP18, Reference Kashiwara, Kim, Oh and ParkKKOP18, Reference Kashiwara and KimKK19, Reference Gross, Hacking, Keel and KontsevichGHKK18] for more details.
2.1 Quantum cluster algebras
Fix a finite index set ![]() $\mathsf {K} = {\mathsf {K}_\mathrm {ex}} \sqcup {\mathsf {K}_\mathrm {fr}}$ with a decomposition into the set
$\mathsf {K} = {\mathsf {K}_\mathrm {ex}} \sqcup {\mathsf {K}_\mathrm {fr}}$ with a decomposition into the set ![]() ${\mathsf {K}_\mathrm {ex}}$ of exchangeable indices and the set
${\mathsf {K}_\mathrm {ex}}$ of exchangeable indices and the set ![]() ${\mathsf {K}_\mathrm {fr}}$ of frozen indices. Let
${\mathsf {K}_\mathrm {fr}}$ of frozen indices. Let ![]() $L = (l_{ij})_{i,j \in \mathsf {K}}$ be a skew-symmetric integer-valued matrix and let
$L = (l_{ij})_{i,j \in \mathsf {K}}$ be a skew-symmetric integer-valued matrix and let ![]() $q$ be an indeterminate. We set
$q$ be an indeterminate. We set ![]() $\mathbb {A} \mathbin {:=} \mathbb {Z}\mspace {1mu}[q^{\pm 1/2}]$ where
$\mathbb {A} \mathbin {:=} \mathbb {Z}\mspace {1mu}[q^{\pm 1/2}]$ where ![]() $q^{1/2}$ denotes the formal square root of
$q^{1/2}$ denotes the formal square root of ![]() $q$.
$q$.
Definition 2.1 We define the quantum torus ![]() $\mathcal {T}(L)$ to be the
$\mathcal {T}(L)$ to be the ![]() $\mathbb {A}$-algebra generated by a finite family of elements
$\mathbb {A}$-algebra generated by a finite family of elements ![]() $\{X^{\pm 1}_k \}_{k \in \mathsf {K}}$ subject to the following defining relations:
$\{X^{\pm 1}_k \}_{k \in \mathsf {K}}$ subject to the following defining relations:
For ![]() $\mathbf {a} = (\mathbf {a}_i)_{i \in \mathsf {K}} \in \mathbb {Z}\mspace {1mu}^\mathsf {K}$, we define the element
$\mathbf {a} = (\mathbf {a}_i)_{i \in \mathsf {K}} \in \mathbb {Z}\mspace {1mu}^\mathsf {K}$, we define the element ![]() $X^\mathbf {a}$ of
$X^\mathbf {a}$ of ![]() $\mathcal {T}(L)$ as
$\mathcal {T}(L)$ as
 \[ X^\mathbf{a} = q^{({1/2}) \sum_{i>j}\mathbf{a}_i\mathbf{a}_j l_{ij}} \prod^{\longrightarrow}_{i \in \mathsf{K}} X_i^{\mathbf{a}_i}. \]
\[ X^\mathbf{a} = q^{({1/2}) \sum_{i>j}\mathbf{a}_i\mathbf{a}_j l_{ij}} \prod^{\longrightarrow}_{i \in \mathsf{K}} X_i^{\mathbf{a}_i}. \]
Here ![]() $\overset {\longrightarrow }{\prod }_{i \in \mathsf {K}} X_i^{\mathbf {a}_i} \mathbin {:=} X_{i_1}^{\mathbf {a}_{i_1}} \cdots X_{i_r}^{\mathbf {a}_{i_r}}$, where
$\overset {\longrightarrow }{\prod }_{i \in \mathsf {K}} X_i^{\mathbf {a}_i} \mathbin {:=} X_{i_1}^{\mathbf {a}_{i_1}} \cdots X_{i_r}^{\mathbf {a}_{i_r}}$, where ![]() $\mathsf {K}=\{ i_1,\ldots,i_r \}$ with a total order
$\mathsf {K}=\{ i_1,\ldots,i_r \}$ with a total order ![]() $i_1 < \cdots < i_r$. Note that
$i_1 < \cdots < i_r$. Note that ![]() $X^\mathbf {a}$ does not depend on the choice of a total order < on
$X^\mathbf {a}$ does not depend on the choice of a total order < on ![]() $\mathsf {K}$. Then
$\mathsf {K}$. Then ![]() $\{ X^\mathbf {a} \mid \mathbf {a} \in \mathbb {Z}\mspace {1mu}^{\mathsf {K}} \}$ forms an
$\{ X^\mathbf {a} \mid \mathbf {a} \in \mathbb {Z}\mspace {1mu}^{\mathsf {K}} \}$ forms an ![]() $\mathbb {A}$-basis of
$\mathbb {A}$-basis of ![]() $\mathcal {T}(L)$. Since
$\mathcal {T}(L)$. Since ![]() $\mathcal {T}(L)$ is an Ore domain, it is embedded into the skew field of fractions
$\mathcal {T}(L)$ is an Ore domain, it is embedded into the skew field of fractions ![]() $\mathbb {F}(\mathcal {T}(L))$.
$\mathbb {F}(\mathcal {T}(L))$.
Let ![]() $\widetilde {B} = (b_{ij})_{i \in \mathsf {K},j\in {\mathsf {K}_\mathrm {ex}}}$ be an integer-valued
$\widetilde {B} = (b_{ij})_{i \in \mathsf {K},j\in {\mathsf {K}_\mathrm {ex}}}$ be an integer-valued ![]() $\mathsf {K} \times {\mathsf {K}_\mathrm {ex}}$-matrix whose principal part
$\mathsf {K} \times {\mathsf {K}_\mathrm {ex}}$-matrix whose principal part ![]() $B = (b_{ij})_{i,j\in {\mathsf {K}_\mathrm {ex}}}$ is skew-symmetrizable, i.e. there exists a diagonal matrix
$B = (b_{ij})_{i,j\in {\mathsf {K}_\mathrm {ex}}}$ is skew-symmetrizable, i.e. there exists a diagonal matrix ![]() $D$ with a positive integer entries such that
$D$ with a positive integer entries such that ![]() $DB$ is skew-symmetric. Such a matrix
$DB$ is skew-symmetric. Such a matrix ![]() $\widetilde {B}$ is called an exchange matrix. We say that a pair
$\widetilde {B}$ is called an exchange matrix. We say that a pair ![]() $(L,B)$ is compatible if
$(L,B)$ is compatible if
for some positive integers ![]() $\{ d_i \}_{i \in {\mathsf {K}_\mathrm {ex}}}$. We call the triple
$\{ d_i \}_{i \in {\mathsf {K}_\mathrm {ex}}}$. We call the triple ![]() $\mathcal {S} = (\{ X_k \}_{k \in \mathsf {K}}, L , \widetilde {B} )$ a quantum seed in the quantum torus
$\mathcal {S} = (\{ X_k \}_{k \in \mathsf {K}}, L , \widetilde {B} )$ a quantum seed in the quantum torus ![]() $\mathcal {T}(L)$ and
$\mathcal {T}(L)$ and ![]() $\{ X_k \}_{k \in \mathsf {K}}$ a quantum cluster.
$\{ X_k \}_{k \in \mathsf {K}}$ a quantum cluster.
For ![]() $k \in {\mathsf {K}_\mathrm {ex}}$, the mutation
$k \in {\mathsf {K}_\mathrm {ex}}$, the mutation ![]() $\mu _k(L,\widetilde {B}) \mathbin {:=} (\mu _k(L),\mu _k(B))$ of a compatible pair
$\mu _k(L,\widetilde {B}) \mathbin {:=} (\mu _k(L),\mu _k(B))$ of a compatible pair ![]() $(L,\widetilde {B})$ in a direction
$(L,\widetilde {B})$ in a direction ![]() $k$ is defined in a combinatorial way (see [Reference Berenstein and ZelevinskyBZ05]). Note that (i) the pair
$k$ is defined in a combinatorial way (see [Reference Berenstein and ZelevinskyBZ05]). Note that (i) the pair ![]() $(\mu _k(L),\mu _k(B))$ is also compatible with the same positive integers
$(\mu _k(L),\mu _k(B))$ is also compatible with the same positive integers ![]() $\{d_i\}_{i \in \mathsf {K}}$ and (ii) the operation
$\{d_i\}_{i \in \mathsf {K}}$ and (ii) the operation ![]() $\mu _k$ is an involution, i.e.
$\mu _k$ is an involution, i.e. ![]() $\mu _k(\mu _k(L,\widetilde {B})) = (L,\widetilde {B})$. We define an isomorphism of
$\mu _k(\mu _k(L,\widetilde {B})) = (L,\widetilde {B})$. We define an isomorphism of ![]() $\mathbb {Q}(q^{1/2})$-algebras
$\mathbb {Q}(q^{1/2})$-algebras ![]() $\mu _k^* \colon \mathbb {F}(\mathcal {T}(\mu _kL)) {\mathop\longrightarrow\limits^{\sim}} \mathbb {F}(\mathcal {T}(L))$ by
$\mu _k^* \colon \mathbb {F}(\mathcal {T}(\mu _kL)) {\mathop\longrightarrow\limits^{\sim}} \mathbb {F}(\mathcal {T}(L))$ by
 \[ \mu_k^*(X_j) \mathbin{:=} \begin{cases} X^{\mathbf{a}'} + X^{\mathbf{a}''} & \text{if } j =k, \\ X_j & \text{if } j \ne k, \end{cases} \]
\[ \mu_k^*(X_j) \mathbin{:=} \begin{cases} X^{\mathbf{a}'} + X^{\mathbf{a}''} & \text{if } j =k, \\ X_j & \text{if } j \ne k, \end{cases} \]
where
 \[ \mathbf{a}'_i = \begin{cases} -1 & \text{if } i =k, \\ \max(0,b_{ik}) & \text{if } i \ne k, \end{cases} \quad\text{and}\quad \mathbf{a}''_i = \begin{cases} -1 & \text{if } i =k, \\ \max(0,-b_{ik}) & \text{if } i \ne k. \end{cases} \]
\[ \mathbf{a}'_i = \begin{cases} -1 & \text{if } i =k, \\ \max(0,b_{ik}) & \text{if } i \ne k, \end{cases} \quad\text{and}\quad \mathbf{a}''_i = \begin{cases} -1 & \text{if } i =k, \\ \max(0,-b_{ik}) & \text{if } i \ne k. \end{cases} \]
Then the mutation ![]() $\mu _k(\mathcal {S})$ of the quantum seed
$\mu _k(\mathcal {S})$ of the quantum seed ![]() $\mathcal {S}$ in a direction
$\mathcal {S}$ in a direction ![]() $k$ is defined to be the triple
$k$ is defined to be the triple ![]() $( \{ X_i\}_{i \ne k} \sqcup \{ \mu _k^*(X_k) \}, \mu _k(L), \mu _k(\widetilde {B}))$.
$( \{ X_i\}_{i \ne k} \sqcup \{ \mu _k^*(X_k) \}, \mu _k(L), \mu _k(\widetilde {B}))$.
For a quantum seed ![]() $\mathcal {S}=( \{X_k\}_{k\in \mathsf {K}},L,\widetilde {B})$, an element in
$\mathcal {S}=( \{X_k\}_{k\in \mathsf {K}},L,\widetilde {B})$, an element in ![]() $\mathbb {F}(\mathcal {T}(L))$ is called a quantum cluster variable (respectively, quantum cluster monomial) if it is of the form
$\mathbb {F}(\mathcal {T}(L))$ is called a quantum cluster variable (respectively, quantum cluster monomial) if it is of the form
for some finite sequence ![]() $(k_1,\ldots,k_\ell ) \in \mathsf {K}_\mathrm {ex}^\ell$
$(k_1,\ldots,k_\ell ) \in \mathsf {K}_\mathrm {ex}^\ell$ ![]() $(\ell \in \mathbb {Z}\mspace {1mu}_{\geqslant 0})$ and
$(\ell \in \mathbb {Z}\mspace {1mu}_{\geqslant 0})$ and ![]() $j \in \mathsf {K}$ (respectively,
$j \in \mathsf {K}$ (respectively, ![]() $\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$). For a quantum seed
$\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$). For a quantum seed ![]() $\mathcal {S} = (\{ X_k \}_{k \in \mathsf {K}}, L,\widetilde {B} )$, the quantum cluster algebra
$\mathcal {S} = (\{ X_k \}_{k \in \mathsf {K}}, L,\widetilde {B} )$, the quantum cluster algebra ![]() $\mathscr {A}_q(\mathcal {S})$ is the
$\mathscr {A}_q(\mathcal {S})$ is the ![]() $\mathbb {A}$-subalgebra of
$\mathbb {A}$-subalgebra of ![]() $\mathbb {F}(\mathcal {T}(L))$ generated by all the quantum cluster variables. Note that
$\mathbb {F}(\mathcal {T}(L))$ generated by all the quantum cluster variables. Note that ![]() $\mathscr {A}_q(\mathcal {S})\simeq \mathscr {A}_q(\boldsymbol {\mu }(\mathcal {S}))$ for any sequence
$\mathscr {A}_q(\mathcal {S})\simeq \mathscr {A}_q(\boldsymbol {\mu }(\mathcal {S}))$ for any sequence ![]() $\boldsymbol {\mu }$ of mutations.
$\boldsymbol {\mu }$ of mutations.
The quantum Laurent phenomenon, proved by Berenstein and Zelevinsky in [Reference Berenstein and ZelevinskyBZ05], says that the quantum cluster algebra ![]() $\mathscr {A}_q(\mathcal {S})$ is indeed contained in
$\mathscr {A}_q(\mathcal {S})$ is indeed contained in ![]() $\mathcal {T}(L)$.
$\mathcal {T}(L)$.
For a quantum seed ![]() $\mathcal {S}$ with a compatible pair
$\mathcal {S}$ with a compatible pair ![]() $(L,\widetilde {B})$, an element
$(L,\widetilde {B})$, an element ![]() $\mathbf {x} \in \mathcal {T}(L)$ is called pointed (respectively, copointed) if it is of the following form:
$\mathbf {x} \in \mathcal {T}(L)$ is called pointed (respectively, copointed) if it is of the following form:
 \begin{equation} \mathbf{x} = q^{a} X^{\mathbf{g}^R} + \sum_{ \mathbf{c} \in \mathbb{Z}\mspace{1mu}_{\geqslant 0}^{{\mathsf{K}_\mathrm{ex}}} \setminus \{ 0 \} } p_\mathbf{c} X^{\mathbf{g}^R+\widetilde{B} \mathbf{c}} \quad \bigg(\text{respectively, } \mathbf{x} = q^{a} X^{\mathbf{g}^L} + \sum_{ \mathbf{c} \in \mathbb{Z}\mspace{1mu}_{\leqslant 0}^{{\mathsf{K}_\mathrm{ex}}} \setminus \{ 0 \} } p_\mathbf{c} X^{\mathbf{g}^L+\widetilde{B} \mathbf{c}}\bigg) \end{equation}
\begin{equation} \mathbf{x} = q^{a} X^{\mathbf{g}^R} + \sum_{ \mathbf{c} \in \mathbb{Z}\mspace{1mu}_{\geqslant 0}^{{\mathsf{K}_\mathrm{ex}}} \setminus \{ 0 \} } p_\mathbf{c} X^{\mathbf{g}^R+\widetilde{B} \mathbf{c}} \quad \bigg(\text{respectively, } \mathbf{x} = q^{a} X^{\mathbf{g}^L} + \sum_{ \mathbf{c} \in \mathbb{Z}\mspace{1mu}_{\leqslant 0}^{{\mathsf{K}_\mathrm{ex}}} \setminus \{ 0 \} } p_\mathbf{c} X^{\mathbf{g}^L+\widetilde{B} \mathbf{c}}\bigg) \end{equation}
for some ![]() $a \in \frac {1}{2}\mathbb {Z}\mspace {1mu}$,
$a \in \frac {1}{2}\mathbb {Z}\mspace {1mu}$, ![]() $\mathbf {g}^R \in \mathbb {Z}\mspace {1mu}^\mathsf {K}$ (respectively,
$\mathbf {g}^R \in \mathbb {Z}\mspace {1mu}^\mathsf {K}$ (respectively, ![]() $\mathbf {g}^L \in \mathbb {Z}\mspace {1mu}^\mathsf {K}$) and
$\mathbf {g}^L \in \mathbb {Z}\mspace {1mu}^\mathsf {K}$) and ![]() $p_\mathbf {c} \in \mathbb {A}$. In this case, we call
$p_\mathbf {c} \in \mathbb {A}$. In this case, we call ![]() $\mathbf {g}^R$ the degree (respectively, codegree) of the pointed (respectively, copointed) element
$\mathbf {g}^R$ the degree (respectively, codegree) of the pointed (respectively, copointed) element ![]() $\mathbf {x}$ and denote it by
$\mathbf {x}$ and denote it by ![]() $\mathbf {deg}_{\mathcal {S}}(\mathbf {x})$ (respectively,
$\mathbf {deg}_{\mathcal {S}}(\mathbf {x})$ (respectively, ![]() $\mathbf {codeg}_{\mathcal {S}}(\mathbf {x})$). The degree (respectively, codegree) is often the called
$\mathbf {codeg}_{\mathcal {S}}(\mathbf {x})$). The degree (respectively, codegree) is often the called ![]() $g$-vector (respectively, dual
$g$-vector (respectively, dual ![]() $g$-vector) of
$g$-vector) of ![]() $\mathbf {x}$ (see [Reference QinQin17, Definition 3.1.4] and [Reference QinQin20, Definition 3.1.3]). It is worth remarking that the notion of
$\mathbf {x}$ (see [Reference QinQin17, Definition 3.1.4] and [Reference QinQin20, Definition 3.1.3]). It is worth remarking that the notion of ![]() $g$-vector (respectively, dual
$g$-vector (respectively, dual ![]() $g$-vector) does depend on the compatible pair
$g$-vector) does depend on the compatible pair ![]() $(L,\widetilde {B})$ and, hence, on the seed
$(L,\widetilde {B})$ and, hence, on the seed ![]() $\mathcal {S}$. It is proved in [Reference TranTra11, Theorem 5.3] that every quantum cluster monomial in
$\mathcal {S}$. It is proved in [Reference TranTra11, Theorem 5.3] that every quantum cluster monomial in ![]() $\mathscr {A}_q(\mathcal {S})$ is pointed.
$\mathscr {A}_q(\mathcal {S})$ is pointed.
We say that an ![]() $\mathbb {A}$-algebra
$\mathbb {A}$-algebra ![]() $R$ has a quantum cluster algebra structure if there exists a quantum seed
$R$ has a quantum cluster algebra structure if there exists a quantum seed ![]() $\mathcal {S}$ and an
$\mathcal {S}$ and an ![]() $\mathbb {A}$-algebra isomorphism
$\mathbb {A}$-algebra isomorphism ![]() $\Omega : \mathscr {A}_q(\mathcal {S}) {\mathop\longrightarrow\limits^{\sim}} R$. In the case, a quantum seed of
$\Omega : \mathscr {A}_q(\mathcal {S}) {\mathop\longrightarrow\limits^{\sim}} R$. In the case, a quantum seed of ![]() $R$ refers to the image of a quantum seed in
$R$ refers to the image of a quantum seed in ![]() $\mathscr {A}_q(\mathcal {S})$, which is obtained by a sequence of mutations.
$\mathscr {A}_q(\mathcal {S})$, which is obtained by a sequence of mutations.
2.2 Quantum unipotent coordinate rings
Let ![]() $I$ be an index set. A Cartan datum
$I$ be an index set. A Cartan datum ![]() $(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$ consists of:
$(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$ consists of:
(a) a symmetrizable Cartan matrix
 $\mathsf {A}=(a_{i,j})_{i,j \in I}$, i.e.
$\mathsf {A}=(a_{i,j})_{i,j \in I}$, i.e.  $\mathsf {D} \mathsf {A}$ is symmetric for a diagonal matrix
$\mathsf {D} \mathsf {A}$ is symmetric for a diagonal matrix  $\mathsf {D} = {\rm diag}(\mathsf {d}_i \mid i \in I)$ with
$\mathsf {D} = {\rm diag}(\mathsf {d}_i \mid i \in I)$ with  $\mathsf {d}_i\in \mathbb {Z}\mspace {1mu}_{>0}$;
$\mathsf {d}_i\in \mathbb {Z}\mspace {1mu}_{>0}$;(b) a free abelian group
 $\mathsf {P}$, called the weight lattice;
$\mathsf {P}$, called the weight lattice;(c)
 $\Pi = \{{\mspace {1mu}\alpha }_i \mid i \in I \} \subset \mathsf {P}$, called the set of simple roots;
$\Pi = \{{\mspace {1mu}\alpha }_i \mid i \in I \} \subset \mathsf {P}$, called the set of simple roots;(d)
 $\Pi ^\vee = \{ h_i \mid i \in I \} \subset \mathsf {P}^\vee \mathbin {:=} \operatorname {Hom}(\mathsf {P},\mathbb {Z}\mspace {1mu})$, called the set of simple coroots;
$\Pi ^\vee = \{ h_i \mid i \in I \} \subset \mathsf {P}^\vee \mathbin {:=} \operatorname {Hom}(\mathsf {P},\mathbb {Z}\mspace {1mu})$, called the set of simple coroots;(e) a
 $\mathbb {Q}$-valued symmetric bilinear form
$\mathbb {Q}$-valued symmetric bilinear form  $( \cdot,\cdot )$ on
$( \cdot,\cdot )$ on  $\mathsf {P}$;
$\mathsf {P}$;
satisfying the standard properties (see [Reference Kang, Kashiwara, Kim and OhKKKO18, § 1.1] for instance). Here we take ![]() $\mathsf {D} ={\rm diag}(\mathsf {d}_i \mid i \in I)$ such that
$\mathsf {D} ={\rm diag}(\mathsf {d}_i \mid i \in I)$ such that ![]() $\mathsf {d}_i \mathbin {:=}({\mspace {1mu}\alpha }_i,{\mspace {1mu}\alpha }_i)/2\in \mathbb {Z}\mspace {1mu}_{>0}$
$\mathsf {d}_i \mathbin {:=}({\mspace {1mu}\alpha }_i,{\mspace {1mu}\alpha }_i)/2\in \mathbb {Z}\mspace {1mu}_{>0}$ ![]() $(i\in I)$ in this paper.
$(i\in I)$ in this paper.
For ![]() $i \in I$, we choose
$i \in I$, we choose ![]() $\varpi _i \in \mathsf {P}$ such that
$\varpi _i \in \mathsf {P}$ such that ![]() $\langle h_i,\varpi _j \rangle =\delta _{ij}$ for any
$\langle h_i,\varpi _j \rangle =\delta _{ij}$ for any ![]() $j \in I$ and call it the
$j \in I$ and call it the ![]() $i$th fundamental weight. The free abelian group
$i$th fundamental weight. The free abelian group ![]() $\mathsf {Q} \mathbin {:=} \bigoplus _{i \in I} \mathbb {Z}\mspace {1mu} {\mspace {1mu}\alpha }_i$ is called the root lattice and we set
$\mathsf {Q} \mathbin {:=} \bigoplus _{i \in I} \mathbb {Z}\mspace {1mu} {\mspace {1mu}\alpha }_i$ is called the root lattice and we set ![]() $\mathsf {Q}^+ = \sum _{i \in I}\mathbb {Z}\mspace {1mu}_{\geqslant 0} {\mspace {1mu}\alpha }_i \subset \mathsf {Q}$ and
$\mathsf {Q}^+ = \sum _{i \in I}\mathbb {Z}\mspace {1mu}_{\geqslant 0} {\mspace {1mu}\alpha }_i \subset \mathsf {Q}$ and ![]() $\mathsf {Q}^- = \sum _{i \in I}\mathbb {Z}\mspace {1mu}_{\leqslant 0} {\mspace {1mu}\alpha }_i \subset \mathsf {Q}$. We denote by
$\mathsf {Q}^- = \sum _{i \in I}\mathbb {Z}\mspace {1mu}_{\leqslant 0} {\mspace {1mu}\alpha }_i \subset \mathsf {Q}$. We denote by ![]() $\Delta$ the set of roots and by
$\Delta$ the set of roots and by ![]() $\Delta ^\pm$ the set of positive roots (respectively, negative roots). For
$\Delta ^\pm$ the set of positive roots (respectively, negative roots). For ![]() ${\mspace {1mu}\beta } \in \sum _{i \in I} m_i{\mspace {1mu}\alpha }_i \in \mathsf {Q}^+$, we set
${\mspace {1mu}\beta } \in \sum _{i \in I} m_i{\mspace {1mu}\alpha }_i \in \mathsf {Q}^+$, we set ![]() $|{\mspace {1mu}\beta }| \mathbin {:=} \sum _{i \in I} m_i$,
$|{\mspace {1mu}\beta }| \mathbin {:=} \sum _{i \in I} m_i$, ![]() ${\rm supp}({\mspace {1mu}\beta }) \mathbin {:=}\{ i \in I \mid m_i \ne 0 \}$ and
${\rm supp}({\mspace {1mu}\beta }) \mathbin {:=}\{ i \in I \mid m_i \ne 0 \}$ and ![]() $I^{\mspace {1mu}\beta } \mathbin {:=} \{ \nu = (\nu _1, \ldots,\nu _{|{\mspace {1mu}\beta }|}) \in I^{|{\mspace {1mu}\beta }|} \mid {\mspace {1mu}\alpha }_{\nu _1}+ \cdots + {\mspace {1mu}\alpha }_{\nu _{|{\mspace {1mu}\beta }|}} ={\mspace {1mu}\beta } \}$. Note that the symmetric group
$I^{\mspace {1mu}\beta } \mathbin {:=} \{ \nu = (\nu _1, \ldots,\nu _{|{\mspace {1mu}\beta }|}) \in I^{|{\mspace {1mu}\beta }|} \mid {\mspace {1mu}\alpha }_{\nu _1}+ \cdots + {\mspace {1mu}\alpha }_{\nu _{|{\mspace {1mu}\beta }|}} ={\mspace {1mu}\beta } \}$. Note that the symmetric group ![]() $\mathfrak {S}_{|{\mspace {1mu}\beta }|} = \langle r_{1},\ldots, r_{|{\mspace {1mu}\beta }|} \rangle$ acts on
$\mathfrak {S}_{|{\mspace {1mu}\beta }|} = \langle r_{1},\ldots, r_{|{\mspace {1mu}\beta }|} \rangle$ acts on ![]() $I^{\mspace {1mu}\beta }$ by the place permutations.
$I^{\mspace {1mu}\beta }$ by the place permutations.
Let ![]() $\mathfrak {g}$ be the Kac–Moody algebra associated with the Cartan datum
$\mathfrak {g}$ be the Kac–Moody algebra associated with the Cartan datum ![]() $(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$, and
$(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$, and ![]() $\mathsf {W}$ the Weyl group of
$\mathsf {W}$ the Weyl group of ![]() $\mathfrak {g}$. It is generated by the simple reflections
$\mathfrak {g}$. It is generated by the simple reflections ![]() $s_i\in \operatorname {Aut}(\mathsf {P})$
$s_i\in \operatorname {Aut}(\mathsf {P})$ ![]() $(i \in I)$ defined by
$(i \in I)$ defined by ![]() $s_i(\lambda ) = \lambda - \langle h_i,\lambda \rangle {\mspace {1mu}\alpha }_i$ for
$s_i(\lambda ) = \lambda - \langle h_i,\lambda \rangle {\mspace {1mu}\alpha }_i$ for ![]() $\lambda \in \mathsf {P}$. For a sequence
$\lambda \in \mathsf {P}$. For a sequence ![]() ${\boldsymbol {i}}=(i_1,\ldots,i_r) \in I^r$, we call it a reduced sequence of
${\boldsymbol {i}}=(i_1,\ldots,i_r) \in I^r$, we call it a reduced sequence of ![]() $w \in \mathsf {W}$ if
$w \in \mathsf {W}$ if ![]() $s_{i_1} \ldots s_{i_r}$ is a reduced expression of
$s_{i_1} \ldots s_{i_r}$ is a reduced expression of ![]() $w$. For
$w$. For ![]() $w,v \in \mathsf {W}$, we write
$w,v \in \mathsf {W}$, we write ![]() $w \geqslant v$ if there is a reduced sequence of
$w \geqslant v$ if there is a reduced sequence of ![]() $v$ which appears in a reduced sequence of
$v$ which appears in a reduced sequence of ![]() $w$ as a subsequence.
$w$ as a subsequence.
For ![]() $\lambda,\mu \in \mathsf {P}$, we write
$\lambda,\mu \in \mathsf {P}$, we write ![]() $\lambda \preccurlyeq \mu$ if there exists a sequence of real positive roots
$\lambda \preccurlyeq \mu$ if there exists a sequence of real positive roots ![]() ${\mspace {1mu}\beta }_k$
${\mspace {1mu}\beta }_k$ ![]() $(1 \leqslant k \leqslant l)$ such that
$(1 \leqslant k \leqslant l)$ such that ![]() $\lambda = s_{{\mspace {1mu}\beta }_l} \cdots s_{{\mspace {1mu}\beta }_1} \mu$ and
$\lambda = s_{{\mspace {1mu}\beta }_l} \cdots s_{{\mspace {1mu}\beta }_1} \mu$ and ![]() $({\mspace {1mu}\beta }_k,s_{{\mspace {1mu}\beta }_{k-1}} \cdots s_{{\mspace {1mu}\beta }_1}\mu )>0$ for
$({\mspace {1mu}\beta }_k,s_{{\mspace {1mu}\beta }_{k-1}} \cdots s_{{\mspace {1mu}\beta }_1}\mu )>0$ for ![]() $1 \leqslant k \leqslant l$. When
$1 \leqslant k \leqslant l$. When ![]() $\Lambda \in \mathsf {P}^+$ and
$\Lambda \in \mathsf {P}^+$ and ![]() $\lambda,\mu \in \mathsf {W}\Lambda$ the relation
$\lambda,\mu \in \mathsf {W}\Lambda$ the relation ![]() $\lambda \preccurlyeq \mu$ holds if and only if there exist
$\lambda \preccurlyeq \mu$ holds if and only if there exist ![]() $w,v \in \mathsf {W}$ such that
$w,v \in \mathsf {W}$ such that ![]() $\lambda = w\Lambda$,
$\lambda = w\Lambda$, ![]() $\mu = v\Lambda$ and
$\mu = v\Lambda$ and ![]() $v \leqslant w$.
$v \leqslant w$.
Let ![]() $\mathcal {U}_q(\mathfrak {g})$ be the quantum group of
$\mathcal {U}_q(\mathfrak {g})$ be the quantum group of ![]() $\mathfrak {g}$ over
$\mathfrak {g}$ over ![]() $\mathbb {Q}(q^{1/2})$, generated by
$\mathbb {Q}(q^{1/2})$, generated by ![]() $e_i,f_i$
$e_i,f_i$ ![]() $(i \in I)$ and
$(i \in I)$ and ![]() $q^h$
$q^h$ ![]() $(h \in \mathsf {P}^\vee )$. We denote by
$(h \in \mathsf {P}^\vee )$. We denote by ![]() $\mathcal {U}_q^+(\mathfrak {g})$ the subalgebra of
$\mathcal {U}_q^+(\mathfrak {g})$ the subalgebra of ![]() $\mathcal {U}_q(\mathfrak {g})$ generated by
$\mathcal {U}_q(\mathfrak {g})$ generated by ![]() $e_i$ and
$e_i$ and ![]() $\mathcal {U}_{\mathbb {A}}^+(\mathfrak {g})$ the
$\mathcal {U}_{\mathbb {A}}^+(\mathfrak {g})$ the ![]() $\mathbb {A}$-subalgebra of
$\mathbb {A}$-subalgebra of ![]() $\mathcal {U}_q(\mathfrak {g})^+$ generated by
$\mathcal {U}_q(\mathfrak {g})^+$ generated by ![]() $e_i^n/[n]_i !$
$e_i^n/[n]_i !$ ![]() $(i \in I, \; n \in \mathbb {Z}\mspace {1mu}_{>0})$, where
$(i \in I, \; n \in \mathbb {Z}\mspace {1mu}_{>0})$, where
 \begin{align*} q_i \mathbin{:=} q^{\mathsf{d}_i}, \quad [k]_i = \dfrac{q_i^k-q_i^{-k}}{q_i - q_i^{-1}} \quad\text{and}\quad [k]_i! = \prod_{s=1}^k [s]_i. \end{align*}
\begin{align*} q_i \mathbin{:=} q^{\mathsf{d}_i}, \quad [k]_i = \dfrac{q_i^k-q_i^{-k}}{q_i - q_i^{-1}} \quad\text{and}\quad [k]_i! = \prod_{s=1}^k [s]_i. \end{align*}
Set
where ![]() $\mathcal {U}^+_q(\mathfrak {g})_{-\beta }$ denotes the
$\mathcal {U}^+_q(\mathfrak {g})_{-\beta }$ denotes the ![]() $(-{\mspace {1mu}\beta })$-root space of
$(-{\mspace {1mu}\beta })$-root space of ![]() $\mathcal {U}^+_q(\mathfrak {g})$. Then
$\mathcal {U}^+_q(\mathfrak {g})$. Then ![]() $\mathcal {A}_q(\mathfrak {n})$ also has an algebra structure and is called the quantum unipotent coordinate ring of
$\mathcal {A}_q(\mathfrak {n})$ also has an algebra structure and is called the quantum unipotent coordinate ring of ![]() $\mathfrak {g}$. We denote by
$\mathfrak {g}$. We denote by ![]() $\mathcal {A}_{\mathbb {A}}(\mathfrak {n})$ the
$\mathcal {A}_{\mathbb {A}}(\mathfrak {n})$ the ![]() $\mathbb {A}$-submodule of
$\mathbb {A}$-submodule of ![]() $\mathcal {A}_q(\mathfrak {n})$ generated by
$\mathcal {A}_q(\mathfrak {n})$ generated by ![]() $\psi \in \mathcal {A}_q(\mathfrak {n})$ such that
$\psi \in \mathcal {A}_q(\mathfrak {n})$ such that ![]() $\psi (\mathcal {U}_{\mathbb {A}}^+(\mathfrak {g})) \subset \mathbb {A}$. Then,
$\psi (\mathcal {U}_{\mathbb {A}}^+(\mathfrak {g})) \subset \mathbb {A}$. Then, ![]() $\mathcal {A}_q(\mathfrak {n})$ is an
$\mathcal {A}_q(\mathfrak {n})$ is an ![]() $\mathbb {A}$-subalgebra with a
$\mathbb {A}$-subalgebra with a ![]() $\mathcal {U}_{\mathbb {A}}^+(\mathfrak {g})$-bimodule structure.
$\mathcal {U}_{\mathbb {A}}^+(\mathfrak {g})$-bimodule structure.
For each ![]() $\lambda \in \mathsf {P}^+ \mathbin {:=} \sum _{i \in I} \mathbb {Z}\mspace {1mu}_{\geqslant 0} \varpi _i$ and Weyl group elements
$\lambda \in \mathsf {P}^+ \mathbin {:=} \sum _{i \in I} \mathbb {Z}\mspace {1mu}_{\geqslant 0} \varpi _i$ and Weyl group elements ![]() $w,w' \in \mathsf {W}$, we can define a specific homogeneous element
$w,w' \in \mathsf {W}$, we can define a specific homogeneous element ![]() $D(w\lambda,w'\lambda )$ of
$D(w\lambda,w'\lambda )$ of ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n})$, called a unipotent quantum minor (see, for example, [Reference Kang, Kashiwara, Kim and OhKKKO18, § 9]).
$\mathcal {A}_\mathbb {A}(\mathfrak {n})$, called a unipotent quantum minor (see, for example, [Reference Kang, Kashiwara, Kim and OhKKKO18, § 9]).
For ![]() $w \in \mathsf {W}$, we denote by
$w \in \mathsf {W}$, we denote by ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ the
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ the ![]() $\mathbb {A}$-submodule of
$\mathbb {A}$-submodule of ![]() $\mathcal {A}_{\mathbb {A}}(\mathfrak {n})$ consisting of elements
$\mathcal {A}_{\mathbb {A}}(\mathfrak {n})$ consisting of elements ![]() $\psi$ such that
$\psi$ such that ![]() $e_{i_1} \cdots e_{i_{|{\mspace {1mu}\beta }|}}\psi =0$ for any
$e_{i_1} \cdots e_{i_{|{\mspace {1mu}\beta }|}}\psi =0$ for any ![]() ${\mspace {1mu}\beta } \in \mathsf {Q}^+ \setminus w \mathsf {Q}^-$ and
${\mspace {1mu}\beta } \in \mathsf {Q}^+ \setminus w \mathsf {Q}^-$ and ![]() $(\nu _{i_1},\ldots,\nu _{i_{|{\mspace {1mu}\beta }|}}) \in I^{\mspace {1mu}\beta }$. Then it is an
$(\nu _{i_1},\ldots,\nu _{i_{|{\mspace {1mu}\beta }|}}) \in I^{\mspace {1mu}\beta }$. Then it is an ![]() $\mathbb {A}$-subalgebra and we call it the quantum unipotent coordinate ring associated with
$\mathbb {A}$-subalgebra and we call it the quantum unipotent coordinate ring associated with ![]() $w$.
$w$.
For a reduced sequence ![]() ${\boldsymbol {i}}=(i_1,\ldots,i_r)$ of
${\boldsymbol {i}}=(i_1,\ldots,i_r)$ of ![]() $w \in \mathsf {W}$ and
$w \in \mathsf {W}$ and ![]() $1 \leqslant k \leqslant r$, define
$1 \leqslant k \leqslant r$, define ![]() $w^{{\boldsymbol {i}}}_{\leqslant k}=s_{i_1} \cdots s_{i_k}$ and
$w^{{\boldsymbol {i}}}_{\leqslant k}=s_{i_1} \cdots s_{i_k}$ and ![]() $w^{\boldsymbol {i}}_{< k}=s_{i_1}\cdots s_{i_{k-1}}$. Then
$w^{\boldsymbol {i}}_{< k}=s_{i_1}\cdots s_{i_{k-1}}$. Then ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ is generated by the set of unipotent quantum minors
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ is generated by the set of unipotent quantum minors ![]() $\{ D(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_{k}}, w^{\boldsymbol {i}}_{< k}\varpi _{i_{k}}) \mid 1 \leqslant k \leqslant r \}$ as an
$\{ D(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_{k}}, w^{\boldsymbol {i}}_{< k}\varpi _{i_{k}}) \mid 1 \leqslant k \leqslant r \}$ as an ![]() $\mathbb {A}$-algebra.
$\mathbb {A}$-algebra.
It is proved in [Reference Geiss, Leclerc and SchröerGLS13a, Reference Goodearl and YakimovGY17, Reference Kang, Kashiwara, Kim and OhKKKO18, Reference QinQin20] that ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ has a quantum cluster algebra structure, one of whose quantum seeds
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ has a quantum cluster algebra structure, one of whose quantum seeds ![]() $\mathcal {S}^{\boldsymbol {i}}$ can be obtained from a reduced sequence
$\mathcal {S}^{\boldsymbol {i}}$ can be obtained from a reduced sequence ![]() ${\boldsymbol {i}}=(i_1,\ldots,i_r)$ of
${\boldsymbol {i}}=(i_1,\ldots,i_r)$ of ![]() $w$. To introduce
$w$. To introduce ![]() $\mathcal {S}^{\boldsymbol {i}}$, we need preparations.
$\mathcal {S}^{\boldsymbol {i}}$, we need preparations.
Let ![]() ${\boldsymbol {j}}=(j_1,\ldots,j_l)$ be a sequence of indices in
${\boldsymbol {j}}=(j_1,\ldots,j_l)$ be a sequence of indices in ![]() $I$. For
$I$. For ![]() $1 \leqslant k \leqslant l$ and
$1 \leqslant k \leqslant l$ and ![]() $j \in I$, we set
$j \in I$, we set
 \begin{align*} k^{\boldsymbol{j}}_+&\mathbin{:=} \min(\{u\mid k< u \leqslant l,\; j_u=j_k\} \cup \{l+1\}), \\ k^{\boldsymbol{j}}_-&\mathbin{:=} \max(\{u\mid 1\leqslant u < k,\;j_u=j_k\} \cup \{0\}). \end{align*}
\begin{align*} k^{\boldsymbol{j}}_+&\mathbin{:=} \min(\{u\mid k< u \leqslant l,\; j_u=j_k\} \cup \{l+1\}), \\ k^{\boldsymbol{j}}_-&\mathbin{:=} \max(\{u\mid 1\leqslant u < k,\;j_u=j_k\} \cup \{0\}). \end{align*}
We also set
We sometimes drop ![]() $^{\boldsymbol {j}}$ in the above notation if there is no danger of confusion.
$^{\boldsymbol {j}}$ in the above notation if there is no danger of confusion.
Take ![]() $\mathsf {K}=[1,r]$ as an index set and decompose
$\mathsf {K}=[1,r]$ as an index set and decompose ![]() $\mathsf {K}$ into
$\mathsf {K}$ into
We define the ![]() $\mathbb {Z}\mspace {1mu}$-valued
$\mathbb {Z}\mspace {1mu}$-valued ![]() $\mathsf {K}\times {\mathsf {K}_\mathrm {ex}}$ matrix
$\mathsf {K}\times {\mathsf {K}_\mathrm {ex}}$ matrix ![]() $\widetilde {B}^{\boldsymbol {i}} =(b^{\boldsymbol {i}}_{st})_{s\in \mathsf {K},t\in {\mathsf {K}_\mathrm {ex}}}$ and the
$\widetilde {B}^{\boldsymbol {i}} =(b^{\boldsymbol {i}}_{st})_{s\in \mathsf {K},t\in {\mathsf {K}_\mathrm {ex}}}$ and the ![]() $\mathbb {Z}\mspace {1mu}$-valued skew-symmetric
$\mathbb {Z}\mspace {1mu}$-valued skew-symmetric ![]() $\mathsf {K}\times \mathsf {K}$ matrix
$\mathsf {K}\times \mathsf {K}$ matrix ![]() $L^{\boldsymbol {i}}=(l^{\boldsymbol {i}}_{st})_{s,t \in \mathsf {K}}$ as follows:
$L^{\boldsymbol {i}}=(l^{\boldsymbol {i}}_{st})_{s,t \in \mathsf {K}}$ as follows:
 \begin{align*} b^{\boldsymbol{i}}_{st} &= \begin{cases} \pm 1 & \text{if $s=t^{\boldsymbol{i}}_\pm$,} \\ -a_{i_s,i_t} & \text{if $s< t< s^{\boldsymbol{i}}_+< t^{\boldsymbol{i}}_+$,}\\ a_{i_s,i_t} & \text{if $t< s< t^{\boldsymbol{i}}_+< s^{\boldsymbol{i}}_+$,} \\ 0 & \text{otherwise}, \end{cases} \\ l^{\boldsymbol{i}}_{st} & = (\varpi_{i_s}-w^{\boldsymbol{i}}_{\leqslant s}\varpi_{i_s}, \varpi_{i_t}+w^{\boldsymbol{i}}_{\leqslant t}\varpi_{i_t} )\quad\text{for } s< t. \end{align*}
\begin{align*} b^{\boldsymbol{i}}_{st} &= \begin{cases} \pm 1 & \text{if $s=t^{\boldsymbol{i}}_\pm$,} \\ -a_{i_s,i_t} & \text{if $s< t< s^{\boldsymbol{i}}_+< t^{\boldsymbol{i}}_+$,}\\ a_{i_s,i_t} & \text{if $t< s< t^{\boldsymbol{i}}_+< s^{\boldsymbol{i}}_+$,} \\ 0 & \text{otherwise}, \end{cases} \\ l^{\boldsymbol{i}}_{st} & = (\varpi_{i_s}-w^{\boldsymbol{i}}_{\leqslant s}\varpi_{i_s}, \varpi_{i_t}+w^{\boldsymbol{i}}_{\leqslant t}\varpi_{i_t} )\quad\text{for } s< t. \end{align*}
Then the quantum seed ![]() $\mathcal {S}^{\boldsymbol {i}}$ of
$\mathcal {S}^{\boldsymbol {i}}$ of ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ is given as follows:
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ is given as follows:
where ![]() $c^{\boldsymbol {i}}_s = \frac {1}{4} (\varpi _{i_s}-w^{\boldsymbol {i}}_{\leqslant s}\varpi _{i_s} ,\varpi _{i_s}-w^{\boldsymbol {i}}_{\leqslant s}\varpi _{i_s} ) \in \mathbb {Z}\mspace {1mu}/2$. Note that
$c^{\boldsymbol {i}}_s = \frac {1}{4} (\varpi _{i_s}-w^{\boldsymbol {i}}_{\leqslant s}\varpi _{i_s} ,\varpi _{i_s}-w^{\boldsymbol {i}}_{\leqslant s}\varpi _{i_s} ) \in \mathbb {Z}\mspace {1mu}/2$. Note that ![]() $(L^{\boldsymbol {i}}\widetilde {B}^{\boldsymbol {i}})_{ab} = -2 \mathsf {d}_{i_a} \times \delta _{a,b}$ for
$(L^{\boldsymbol {i}}\widetilde {B}^{\boldsymbol {i}})_{ab} = -2 \mathsf {d}_{i_a} \times \delta _{a,b}$ for ![]() $(a,b)\in \mathsf {K}\times {\mathsf {K}_\mathrm {ex}}$,
$(a,b)\in \mathsf {K}\times {\mathsf {K}_\mathrm {ex}}$, ![]() ${\rm wt}(D(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},\varpi _{i_k} )) = - \varpi _{i_s} + w^{\boldsymbol {i}}_{\leqslant s}\varpi _{i_s}$, and
${\rm wt}(D(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},\varpi _{i_k} )) = - \varpi _{i_s} + w^{\boldsymbol {i}}_{\leqslant s}\varpi _{i_s}$, and
forms the set of frozen variables of the quantum cluster algebra ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$. We call
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$. We call ![]() $\mathcal {S}^{\boldsymbol {i}}$ the GLS seed (associated with
$\mathcal {S}^{\boldsymbol {i}}$ the GLS seed (associated with ![]() ${\boldsymbol {i}}$).
${\boldsymbol {i}}$).
We set ![]() $\mathcal {D}(w) \mathbin {:=} \{ q^m D(w\varpi,\varpi ) \mid m \in \mathbb {Z}\mspace {1mu}/2, \; \varpi \in \mathsf {P}^+ \}$. Then it is well-known that
$\mathcal {D}(w) \mathbin {:=} \{ q^m D(w\varpi,\varpi ) \mid m \in \mathbb {Z}\mspace {1mu}/2, \; \varpi \in \mathsf {P}^+ \}$. Then it is well-known that ![]() $\mathcal {D}(w)$ consists of
$\mathcal {D}(w)$ consists of ![]() $q$-central elements of
$q$-central elements of ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ and, hence, forms an Ore set. We denote by
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ and, hence, forms an Ore set. We denote by ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}^w)$ the quotient ring of
$\mathcal {A}_\mathbb {A}(\mathfrak {n}^w)$ the quotient ring of ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ by the Ore set
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$ by the Ore set ![]() $\mathcal {D}(w)$. Then
$\mathcal {D}(w)$. Then ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}^w)$ has also the quantum cluster algebra structure with the invertible frozen variables
$\mathcal {A}_\mathbb {A}(\mathfrak {n}^w)$ has also the quantum cluster algebra structure with the invertible frozen variables ![]() $\{ q^{c^{\boldsymbol {i}}_k} D(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},\varpi _{i_k}) \}_{k \in {\mathsf {K}_\mathrm {fr}}}$ in the sense of [Reference Berenstein and ZelevinskyBZ05].
$\{ q^{c^{\boldsymbol {i}}_k} D(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},\varpi _{i_k}) \}_{k \in {\mathsf {K}_\mathrm {fr}}}$ in the sense of [Reference Berenstein and ZelevinskyBZ05].
2.3 Quiver Hecke algebras and categorifications
Let ![]() $\mathbf {k}$ be a base field. For
$\mathbf {k}$ be a base field. For ![]() $i,j \in I$, we choose polynomials
$i,j \in I$, we choose polynomials ![]() $\mathcal {Q}_{i,j}(u,v) \in \mathbf {k}[u,v]$ such that (a)
$\mathcal {Q}_{i,j}(u,v) \in \mathbf {k}[u,v]$ such that (a) ![]() $\mathcal {Q}_{i,j}(u,v) =\mathcal {Q}_{j,i}(v,u)$ and (b) each
$\mathcal {Q}_{i,j}(u,v) =\mathcal {Q}_{j,i}(v,u)$ and (b) each ![]() $\mathcal {Q}_{i,j}(u,v)$ is of the following form:
$\mathcal {Q}_{i,j}(u,v)$ is of the following form:
For a Cartan datum ![]() $(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$ and
$(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$ and ![]() ${\mspace {1mu}\beta } \in \mathsf {Q}^+$, the quiver Hecke algebra
${\mspace {1mu}\beta } \in \mathsf {Q}^+$, the quiver Hecke algebra ![]() $R({\mspace {1mu}\beta })$ associated with
$R({\mspace {1mu}\beta })$ associated with ![]() $(\mathcal {Q}_{i,j})_{i,j \in I}$ is the
$(\mathcal {Q}_{i,j})_{i,j \in I}$ is the ![]() $\mathbb {Z}\mspace {1mu}$-graded algebra over
$\mathbb {Z}\mspace {1mu}$-graded algebra over ![]() $\mathbf {k}$ generated by the elements
$\mathbf {k}$ generated by the elements
subject to certain defining relations (see [Reference Kashiwara, Kim, Oh and ParkKKOP21, Definition 1.1] for instance). Note that the ![]() $\mathbb {Z}\mspace {1mu}$-grading of
$\mathbb {Z}\mspace {1mu}$-grading of ![]() $R({\mspace {1mu}\beta })$ is determined by the degrees of following elements:
$R({\mspace {1mu}\beta })$ is determined by the degrees of following elements:
We say that ![]() $R({\mspace {1mu}\beta })$ is symmetric if
$R({\mspace {1mu}\beta })$ is symmetric if ![]() $\mathcal {Q}_{i,j}(u,v) \in \mathbf {k}[u-v]$ for
$\mathcal {Q}_{i,j}(u,v) \in \mathbf {k}[u-v]$ for ![]() $i,j \in {\rm supp}({\mspace {1mu}\beta })$.
$i,j \in {\rm supp}({\mspace {1mu}\beta })$.
We denote by ![]() $R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$ the category of finite-dimensional graded
$R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$ the category of finite-dimensional graded ![]() $R({\mspace {1mu}\beta })$-modules with homomorphisms of degree
$R({\mspace {1mu}\beta })$-modules with homomorphisms of degree ![]() $0$. For
$0$. For ![]() $M \in R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$, we set
$M \in R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$, we set ![]() ${\rm wt}(M) \mathbin {:=} -{\mspace {1mu}\beta } \in \mathsf {Q}^-$. Note that there exists the degree shift functor, denoted by
${\rm wt}(M) \mathbin {:=} -{\mspace {1mu}\beta } \in \mathsf {Q}^-$. Note that there exists the degree shift functor, denoted by ![]() $q$, such that
$q$, such that ![]() $(qM)_n = M_{n-1}$ for
$(qM)_n = M_{n-1}$ for ![]() $M=\oplus_{k \in \mathbb {Z}\mspace {1mu}} M_k \in R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$.
$M=\oplus_{k \in \mathbb {Z}\mspace {1mu}} M_k \in R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$.
Throughout this paper, we usually deal with graded ![]() $R({\mspace {1mu}\beta })$-modules
$R({\mspace {1mu}\beta })$-modules ![]() $({\mspace {1mu}\beta } \in \mathsf {Q}^+)$ and sometimes skip grading shifts. Thus, we usually say that
$({\mspace {1mu}\beta } \in \mathsf {Q}^+)$ and sometimes skip grading shifts. Thus, we usually say that ![]() $M$ is an
$M$ is an ![]() $R$-module instead of saying that
$R$-module instead of saying that ![]() $M$ is a graded
$M$ is a graded ![]() $R({\mspace {1mu}\beta })$-module and
$R({\mspace {1mu}\beta })$-module and ![]() $f\colon M \to N$ is a homomorphism if
$f\colon M \to N$ is a homomorphism if ![]() $f\colon q^aM \to N$ is a morphism in
$f\colon q^aM \to N$ is a morphism in ![]() $R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$. We set
$R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$. We set
with ![]() $\mathrm {H{\scriptstyle OM}}_{R({\mspace {1mu}\beta })}(M,N)_a\mathbin {:=}\operatorname {Hom}_{R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}}(q^aM,N)_a$. We write
$\mathrm {H{\scriptstyle OM}}_{R({\mspace {1mu}\beta })}(M,N)_a\mathbin {:=}\operatorname {Hom}_{R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}}(q^aM,N)_a$. We write ![]() $\deg (f) \mathbin {:=} a$ for an
$\deg (f) \mathbin {:=} a$ for an ![]() $f \in \mathrm {H{\scriptstyle OM}}_{R({\mspace {1mu}\beta })} (M,N)_a$.
$f \in \mathrm {H{\scriptstyle OM}}_{R({\mspace {1mu}\beta })} (M,N)_a$.
For an ![]() $R({\mspace {1mu}\beta })$-module
$R({\mspace {1mu}\beta })$-module ![]() $M$ and an
$M$ and an ![]() $R(\gamma )$-module
$R(\gamma )$-module ![]() $N$, we can obtain
$N$, we can obtain ![]() $R({\mspace {1mu}\beta }+\gamma )$-module
$R({\mspace {1mu}\beta }+\gamma )$-module
where ![]() $e({\mspace {1mu}\beta },\gamma ) \mathbin {:=} \sum _{\nu \in I^{\mspace {1mu}\beta }, \nu ' \in I^\gamma } e(\nu * \nu ') \in R({\mspace {1mu}\beta }+\gamma )$. Here
$e({\mspace {1mu}\beta },\gamma ) \mathbin {:=} \sum _{\nu \in I^{\mspace {1mu}\beta }, \nu ' \in I^\gamma } e(\nu * \nu ') \in R({\mspace {1mu}\beta }+\gamma )$. Here ![]() $\nu *\nu '$ denotes the concatenation of
$\nu *\nu '$ denotes the concatenation of ![]() $\nu$ and
$\nu$ and ![]() $\nu '$, and
$\nu '$, and ![]() $\circ$ is called the convolution product. We say that two simple
$\circ$ is called the convolution product. We say that two simple ![]() $R$-modules
$R$-modules ![]() $M$ and
$M$ and ![]() $N$ strongly commute if
$N$ strongly commute if ![]() $M \circ N$ is simple. If a simple module
$M \circ N$ is simple. If a simple module ![]() $M$ strongly commutes with itself, then
$M$ strongly commutes with itself, then ![]() $M$ is called real. A simple
$M$ is called real. A simple ![]() $R$-module
$R$-module ![]() $M$ is said to be prime if there are no non-trivial simple
$M$ is said to be prime if there are no non-trivial simple ![]() $R$-modules
$R$-modules ![]() $N_1$ and
$N_1$ and ![]() $N_2$ such that
$N_2$ such that ![]() $M \simeq N_1 \circ N_2$.
$M \simeq N_1 \circ N_2$.
For an ![]() $R({\mspace {1mu}\beta })$-module
$R({\mspace {1mu}\beta })$-module ![]() $M$, the dual space
$M$, the dual space ![]() $M^* \mathbin {:=} \operatorname {Hom}_\mathbf {k}(M,\mathbf {k})$ admits an
$M^* \mathbin {:=} \operatorname {Hom}_\mathbf {k}(M,\mathbf {k})$ admits an ![]() $R({\mspace {1mu}\beta })$-module structure via
$R({\mspace {1mu}\beta })$-module structure via
Here ![]() $\psi$ denotes the
$\psi$ denotes the ![]() $\mathbf {k}$-algebra anti-involution
$\mathbf {k}$-algebra anti-involution ![]() $R({\mspace {1mu}\beta })$ which fixes the generators of
$R({\mspace {1mu}\beta })$ which fixes the generators of ![]() $R({\mspace {1mu}\beta })$. A simple
$R({\mspace {1mu}\beta })$. A simple ![]() $R({\mspace {1mu}\beta })$-module
$R({\mspace {1mu}\beta })$-module ![]() $M$ is called self-dual if
$M$ is called self-dual if ![]() $M^* \simeq M$.
$M^* \simeq M$.
Set ![]() $R\text {-}\mathrm {gmod} \mathbin {:=} \oplus_{{\mspace {1mu}\beta } \in \mathsf {Q}^+}R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$. Then the category
$R\text {-}\mathrm {gmod} \mathbin {:=} \oplus_{{\mspace {1mu}\beta } \in \mathsf {Q}^+}R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$. Then the category ![]() $R\text {-}\mathrm {gmod}$ is a monoidal category with the tensor product
$R\text {-}\mathrm {gmod}$ is a monoidal category with the tensor product ![]() $\circ$ and the unit object
$\circ$ and the unit object ![]() $\mathbf {1} \mathbin {:=} \mathbf {k} \in R(0)\text {-}\mathrm {gmod}$. Hence, the Grothendieck group
$\mathbf {1} \mathbin {:=} \mathbf {k} \in R(0)\text {-}\mathrm {gmod}$. Hence, the Grothendieck group ![]() $K(R\text {-}\mathrm {gmod} )$ has the
$K(R\text {-}\mathrm {gmod} )$ has the ![]() $\mathbb {Z}\mspace {1mu}[q^{\pm 1}]$-algebra structure derived from
$\mathbb {Z}\mspace {1mu}[q^{\pm 1}]$-algebra structure derived from ![]() $\circ$ and the degree shift functors
$\circ$ and the degree shift functors ![]() $q^{\pm 1}$.
$q^{\pm 1}$.
For a monoidal abelian subcategory ![]() $\mathcal {C}$ of
$\mathcal {C}$ of ![]() $R\text {-}\mathrm {gmod}$ stable by grading shifts, we set
$R\text {-}\mathrm {gmod}$ stable by grading shifts, we set
where ![]() $K(\mathcal {C} )$ denotes the Grothendieck ring of
$K(\mathcal {C} )$ denotes the Grothendieck ring of ![]() $\mathcal {C}$. For a subcategory
$\mathcal {C}$. For a subcategory ![]() $\mathcal {C}$ of
$\mathcal {C}$ of ![]() $R\text {-}\mathrm {gmod}$, we denote by
$R\text {-}\mathrm {gmod}$, we denote by ![]() ${\rm Irr}(\mathcal {C})$ the set of the isomorphism classes of self-dual modules in
${\rm Irr}(\mathcal {C})$ the set of the isomorphism classes of self-dual modules in ![]() $\mathcal {C}$. Note that
$\mathcal {C}$. Note that ![]() ${\rm Irr}(R\text {-}\mathrm {gmod})$ forms an
${\rm Irr}(R\text {-}\mathrm {gmod})$ forms an ![]() $\mathbb {A}$-basis of
$\mathbb {A}$-basis of ![]() $\mathcal {K}_\mathbb {A}(R\text {-}\mathrm {gmod})$.
$\mathcal {K}_\mathbb {A}(R\text {-}\mathrm {gmod})$.
It is proved in [Reference Khovanov and LaudaKL09, Reference Khovanov and LaudaKL11, Reference RouquierRou08] that there exists an ![]() $\mathbb {A}$-algebra isomorphism
$\mathbb {A}$-algebra isomorphism
Proposition 2.2 [Reference Kashiwara, Kim, Oh and ParkKKOP18, Proposition 4.1]
For ![]() $\varpi \in \mathsf {P}^+$ and
$\varpi \in \mathsf {P}^+$ and ![]() $\mu,\zeta \in \mathsf {W} \varpi$ with
$\mu,\zeta \in \mathsf {W} \varpi$ with ![]() $\mu \preccurlyeq \zeta$, there exists a self-dual real simple
$\mu \preccurlyeq \zeta$, there exists a self-dual real simple ![]() $R( \zeta -\mu )$-module
$R( \zeta -\mu )$-module ![]() $M(\mu,\zeta )$ such that
$M(\mu,\zeta )$ such that
Here, ![]() $[M(\mu,\zeta )]$ denotes the isomorphism class of
$[M(\mu,\zeta )]$ denotes the isomorphism class of ![]() $M(\mu,\zeta )$ which is called the determinantal module associated with
$M(\mu,\zeta )$ which is called the determinantal module associated with ![]() $D(\mu,\zeta )$.
$D(\mu,\zeta )$.
For an ![]() $R({\mspace {1mu}\beta })$-module
$R({\mspace {1mu}\beta })$-module ![]() $M$, we define
$M$, we define
 \begin{align*} W(M) & \mathbin{:=} \{ \gamma \in \mathsf{Q}^+ \cap ({\mspace{1mu}\beta}-\mathsf{Q}^+) \mid e(\gamma,{\mspace{1mu}\beta}-\gamma)M \ne 0 \}, \\ W^*(M) & \mathbin{:=} \{ \gamma \in \mathsf{Q}^+ \cap ({\mspace{1mu}\beta}-\mathsf{Q}^+) \mid e({\mspace{1mu}\beta}-\gamma,\gamma)M \ne 0 \}. \end{align*}
\begin{align*} W(M) & \mathbin{:=} \{ \gamma \in \mathsf{Q}^+ \cap ({\mspace{1mu}\beta}-\mathsf{Q}^+) \mid e(\gamma,{\mspace{1mu}\beta}-\gamma)M \ne 0 \}, \\ W^*(M) & \mathbin{:=} \{ \gamma \in \mathsf{Q}^+ \cap ({\mspace{1mu}\beta}-\mathsf{Q}^+) \mid e({\mspace{1mu}\beta}-\gamma,\gamma)M \ne 0 \}. \end{align*}
An ordered pair ![]() $(M, N)$ of
$(M, N)$ of ![]() $R$-modules is called unmixed [Reference Tingley and WebsterTW16, Definition 2.5] if
$R$-modules is called unmixed [Reference Tingley and WebsterTW16, Definition 2.5] if
For ![]() $w \in \mathsf {W}$, we denote by
$w \in \mathsf {W}$, we denote by ![]() $\mathscr {C}_w$ the full subcategory of
$\mathscr {C}_w$ the full subcategory of ![]() $R\text {-}\mathrm {gmod}$ whose objects
$R\text {-}\mathrm {gmod}$ whose objects ![]() $M$ satisfy
$M$ satisfy ![]() $W(M) \subset \mathsf {Q}^+ \cap w\mathsf {Q}^-$. Then the category
$W(M) \subset \mathsf {Q}^+ \cap w\mathsf {Q}^-$. Then the category ![]() $\mathscr {C}_w$ is the smallest monoidal abelian category of
$\mathscr {C}_w$ is the smallest monoidal abelian category of ![]() $R\text {-}\mathrm {gmod}$ which (i) is stable under taking subquotients, extensions, grading shifts and (ii) contains
$R\text {-}\mathrm {gmod}$ which (i) is stable under taking subquotients, extensions, grading shifts and (ii) contains ![]() $\big \{ S^{\boldsymbol {i}}_k \mathbin {:=} M(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},w^{\boldsymbol {i}}_{< k}\varpi _{i_k}) \mid 1 \leqslant k \leqslant r \big \}$ for any reduced sequence
$\big \{ S^{\boldsymbol {i}}_k \mathbin {:=} M(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},w^{\boldsymbol {i}}_{< k}\varpi _{i_k}) \mid 1 \leqslant k \leqslant r \big \}$ for any reduced sequence ![]() ${\boldsymbol {i}}$ of
${\boldsymbol {i}}$ of ![]() $w$. We call
$w$. We call ![]() $S^{\boldsymbol {i}}_k$ the
$S^{\boldsymbol {i}}_k$ the ![]() $k$th cuspidal module associated with
$k$th cuspidal module associated with ![]() ${\boldsymbol {i}}$. Defining
${\boldsymbol {i}}$. Defining ![]() ${\mspace {1mu}\beta }_k^{\boldsymbol {i}} \mathbin {:=} w^{\boldsymbol {i}}_{< k} {\mspace {1mu}\alpha }_{i_k}$ for
${\mspace {1mu}\beta }_k^{\boldsymbol {i}} \mathbin {:=} w^{\boldsymbol {i}}_{< k} {\mspace {1mu}\alpha }_{i_k}$ for ![]() $1 \leqslant k \leqslant r$, one can see that
$1 \leqslant k \leqslant r$, one can see that ![]() $\{{\mspace {1mu}\beta }_k^{\boldsymbol {i}} \mid 1\leqslant k\leqslant r\}=\Delta ^+ \cap w \Delta ^-$, and
$\{{\mspace {1mu}\beta }_k^{\boldsymbol {i}} \mid 1\leqslant k\leqslant r\}=\Delta ^+ \cap w \Delta ^-$, and ![]() $-{\rm wt}(S^{\boldsymbol {i}}_k) = {\mspace {1mu}\beta }^{\boldsymbol {i}}_k$. Then we have [Reference KimuraKim12, § 4]
$-{\rm wt}(S^{\boldsymbol {i}}_k) = {\mspace {1mu}\beta }^{\boldsymbol {i}}_k$. Then we have [Reference KimuraKim12, § 4]
2.4  $R$-matrices and affreal simple modules
$R$-matrices and affreal simple modules
For ![]() ${\mspace {1mu}\beta } \in \mathsf {Q}^+$ and
${\mspace {1mu}\beta } \in \mathsf {Q}^+$ and ![]() $i \in I$, let
$i \in I$, let
 \[ \mathfrak{p}_{i,{\mspace{1mu}\beta}} = \sum_{ \eta\, \in I^{\mspace{1mu}\beta}} \bigg( \prod_{a \in [1,|{\mspace{1mu}\beta}|]; \ \eta_a = i} x_a \bigg) e(\eta) \in \mathcal{Z}(R({\mspace{1mu}\beta})), \]
\[ \mathfrak{p}_{i,{\mspace{1mu}\beta}} = \sum_{ \eta\, \in I^{\mspace{1mu}\beta}} \bigg( \prod_{a \in [1,|{\mspace{1mu}\beta}|]; \ \eta_a = i} x_a \bigg) e(\eta) \in \mathcal{Z}(R({\mspace{1mu}\beta})), \]
where ![]() $\mathcal {Z}(R({\mspace {1mu}\beta }))$ denotes the center of
$\mathcal {Z}(R({\mspace {1mu}\beta }))$ denotes the center of ![]() $R({\mspace {1mu}\beta })$.
$R({\mspace {1mu}\beta })$.
Definition 2.3 [Reference Kashiwara and ParkKP18, Definition 2.2]
For an ![]() $R({\mspace {1mu}\beta })$-module
$R({\mspace {1mu}\beta })$-module ![]() $M$, we say that
$M$, we say that ![]() $M$ admits an affinization if there exists an
$M$ admits an affinization if there exists an ![]() $R({\mspace {1mu}\beta })$-module
$R({\mspace {1mu}\beta })$-module ![]() $\widehat {M}$ satisfying the condition: there exists an endomorphism
$\widehat {M}$ satisfying the condition: there exists an endomorphism ![]() $z_{\widehat {M}}$ of degree
$z_{\widehat {M}}$ of degree ![]() $t \in \mathbb {Z}\mspace {1mu}_{>0}$ such that
$t \in \mathbb {Z}\mspace {1mu}_{>0}$ such that ![]() $\widehat {M}/z_{\widehat {M}}\widehat {M} \simeq M$ and:
$\widehat {M}/z_{\widehat {M}}\widehat {M} \simeq M$ and:
(i)
 $\widehat {M}$ is a finitely generated free module over the polynomial ring
$\widehat {M}$ is a finitely generated free module over the polynomial ring  $\mathbf {k}[z_{\widehat {M}}]$;
$\mathbf {k}[z_{\widehat {M}}]$;(ii)
 $\mathfrak {p}_{i,{\mspace {1mu}\beta }} \widehat {M} \ne 0$ for all
$\mathfrak {p}_{i,{\mspace {1mu}\beta }} \widehat {M} \ne 0$ for all  $i \in I$.
$i \in I$.
We say that a simple ![]() $R({\mspace {1mu}\beta })$-module
$R({\mspace {1mu}\beta })$-module ![]() $M$ is affreal if
$M$ is affreal if ![]() $M$ is real and admits an affinization.
$M$ is real and admits an affinization.
It is known that any ![]() $M \in R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$ admits an affinization if
$M \in R({\mspace {1mu}\beta })\text {-}\mathrm {gmod}$ admits an affinization if ![]() $R({\mspace {1mu}\beta })$ is symmetric. However, when
$R({\mspace {1mu}\beta })$ is symmetric. However, when ![]() $R({\mspace {1mu}\beta })$ is not symmetric, it is widely open whether an
$R({\mspace {1mu}\beta })$ is not symmetric, it is widely open whether an ![]() $R({\mspace {1mu}\beta })$-module
$R({\mspace {1mu}\beta })$-module ![]() $M$ admits an affinization or not.
$M$ admits an affinization or not.
Theorem 2.4 [Reference Kashiwara, Kim, Oh and ParkKKOP21, Theorem 3.26]
For ![]() $\varpi \in \mathsf {P}^+$ and
$\varpi \in \mathsf {P}^+$ and ![]() $\mu,\zeta \in \mathsf {W}\varpi$ such that
$\mu,\zeta \in \mathsf {W}\varpi$ such that ![]() $\mu \preccurlyeq \zeta$, the determinantal module
$\mu \preccurlyeq \zeta$, the determinantal module ![]() $M(\mu,\zeta )$ is affreal.
$M(\mu,\zeta )$ is affreal.
Proposition 2.5 [Reference Kang, Kashiwara, Kim and OhKKKO18, Reference Kashiwara, Kim, Oh and ParkKKOP21]
Let ![]() $M$ and
$M$ and ![]() $N$ be simple modules such that one of them is affreal. Then there exists a unique
$N$ be simple modules such that one of them is affreal. Then there exists a unique ![]() $R$-module homomorphism
$R$-module homomorphism ![]() $\mathbf {r}_{M,N} \in \mathrm {H{\scriptstyle OM}}_R(M,N)$ satisfying
$\mathbf {r}_{M,N} \in \mathrm {H{\scriptstyle OM}}_R(M,N)$ satisfying
We call the homomorphism ![]() $\mathbf {r}_{M,N}$ the
$\mathbf {r}_{M,N}$ the ![]() $R$-matrix.
$R$-matrix.
Definition 2.6 For simple ![]() $R$-modules
$R$-modules ![]() $M$ and
$M$ and ![]() $N$ such that one of them is affreal, we define
$N$ such that one of them is affreal, we define
 \begin{align*} \Lambda(M,N) &\mathbin{:=} \deg (\mathbf{r}_{M,N}) , \\ \widetilde{\Lambda}(M,N) &\mathbin{:=} \tfrac{1}{2} \big( \Lambda(M,N) + \big({\rm wt}(M), {\rm wt}(N)\big) \big) , \\ \mathfrak{d}(M,N) &\mathbin{:=} \tfrac{1}{2} \big( \Lambda(M,N) + \Lambda(N,M)\big). \end{align*}
\begin{align*} \Lambda(M,N) &\mathbin{:=} \deg (\mathbf{r}_{M,N}) , \\ \widetilde{\Lambda}(M,N) &\mathbin{:=} \tfrac{1}{2} \big( \Lambda(M,N) + \big({\rm wt}(M), {\rm wt}(N)\big) \big) , \\ \mathfrak{d}(M,N) &\mathbin{:=} \tfrac{1}{2} \big( \Lambda(M,N) + \Lambda(N,M)\big). \end{align*}
It is proved in [Reference Kang, Kashiwara, Kim and OhKKKO18, Reference Kashiwara, Kim, Oh and ParkKKOP21] that the invariants ![]() $\widetilde {\Lambda }(M,N)$ and
$\widetilde {\Lambda }(M,N)$ and ![]() $\mathfrak {d}(M,N)$ in Definition 2.6 belong to
$\mathfrak {d}(M,N)$ in Definition 2.6 belong to ![]() $\mathbb {Z}\mspace {1mu}_{\geqslant 0}$.
$\mathbb {Z}\mspace {1mu}_{\geqslant 0}$.
For simple modules ![]() $M$ and
$M$ and ![]() $N$,
$N$, ![]() $M \triangledown N$ and
$M \triangledown N$ and ![]() $M \triangle N$ denote the head and the socle of
$M \triangle N$ denote the head and the socle of ![]() $M \circ N$, respectively.
$M \circ N$, respectively.
Proposition 2.7 [Reference Kang, Kashiwara, Kim and OhKKKO15, Lemma 3.1.4] and [Reference Kang, Kashiwara, Kim and OhKKKO18, Corollary 4.1.2]
Let ![]() $M$ and
$M$ and ![]() $N$ be simple
$N$ be simple ![]() $R$-modules such that one of them is affreal.
$R$-modules such that one of them is affreal.
(i) The image of
 ${\mathbf r} {M,N}$ is equal to
${\mathbf r} {M,N}$ is equal to  $M\triangledown N$ and
$M\triangledown N$ and  $N\triangle M$.
$N\triangle M$.(ii) The head
 $M \triangledown N$ and socle
$M \triangledown N$ and socle  $M \triangle N$ are simple modules and each of them appears exactly once in the composition series of
$M \triangle N$ are simple modules and each of them appears exactly once in the composition series of  $M \circ N$ (up to a grading shift).
$M \circ N$ (up to a grading shift).(iii) Assume that
 $N$ is affreal.
$N$ is affreal.
(a) If a simple subquotient
 $S$ of
$S$ of  $M \circ N$ is not isomorphic to
$M \circ N$ is not isomorphic to  $M\triangledown N$, then
$M\triangledown N$, then  $\Lambda (S,N)<\Lambda (M\triangledown N,N)=\Lambda (M,N)$.
$\Lambda (S,N)<\Lambda (M\triangledown N,N)=\Lambda (M,N)$.(b) If a simple subquotient
 $S$ of
$S$ of  $M \circ N$ is not isomorphic to
$M \circ N$ is not isomorphic to  $M\triangle N$, then
$M\triangle N$, then  $\Lambda (N,S)<\Lambda (N,M\triangle N)=\Lambda (N,M)$.
$\Lambda (N,S)<\Lambda (N,M\triangle N)=\Lambda (N,M)$.
(iv) If
 $M$ and
$M$ and  $N$ are self-dual, then
$N$ are self-dual, then  $q^{\widetilde {\Lambda }(M,N)} M \triangledown N$ is a self-dual simple module.
$q^{\widetilde {\Lambda }(M,N)} M \triangledown N$ is a self-dual simple module.(v) The following conditions are equivalent:
(a)
 $M \circ N \simeq N \circ M$ up to a grading shift;
$M \circ N \simeq N \circ M$ up to a grading shift;(b)
 $M \circ N$ is simple;
$M \circ N$ is simple;(c)
 $\mathfrak {d}(M,N)=0$;
$\mathfrak {d}(M,N)=0$;(d)
 $M \triangledown N \simeq M \triangle N$ up to a grading shift.
$M \triangledown N \simeq M \triangle N$ up to a grading shift.
Proposition 2.8 [Reference Kashiwara, Kim, Oh and ParkKKOP21, Corollary 3.18]
Let ![]() $M$ be an affreal simple module. Let
$M$ be an affreal simple module. Let ![]() $X$ be an
$X$ be an ![]() $R$-module in
$R$-module in ![]() $R\text {-}\mathrm {gmod}$. Let
$R\text {-}\mathrm {gmod}$. Let ![]() $n \in \mathbb {Z}\mspace {1mu}_{>0}$ and assume that any simple subquotient
$n \in \mathbb {Z}\mspace {1mu}_{>0}$ and assume that any simple subquotient ![]() $S$ of
$S$ of ![]() $X$ satisfies
$X$ satisfies ![]() $\mathfrak {d}(M, S) \leqslant n$. Then any simple subquotient
$\mathfrak {d}(M, S) \leqslant n$. Then any simple subquotient ![]() $N$ of
$N$ of ![]() $M \circ X$ satisfies
$M \circ X$ satisfies ![]() $\mathfrak {d}(M, N) < n$. In particular, any simple subquotient of
$\mathfrak {d}(M, N) < n$. In particular, any simple subquotient of ![]() $M^{\circ n} \circ X$ strongly commutes with
$M^{\circ n} \circ X$ strongly commutes with ![]() $M$.
$M$.
An ordered sequence of simple modules ![]() $\underline {L}=(L_1,\ldots,L_r)$ is called almost affreal if all
$\underline {L}=(L_1,\ldots,L_r)$ is called almost affreal if all ![]() $L_i$
$L_i$ ![]() $(1 \leqslant i \leqslant r)$ are affreal except for at most one.
$(1 \leqslant i \leqslant r)$ are affreal except for at most one.
Definition 2.9 An almost affreal sequence ![]() $\underline {L}$ of simple modules is called a normal sequence if the composition of
$\underline {L}$ of simple modules is called a normal sequence if the composition of ![]() $R$-matrices
$R$-matrices
 \begin{align*} {\mathbf r}{\underline{L}} &
\mathbin{:=} \prod_{1 \leqslant i < k \leqslant r}
{\mathbf r}{L_i,L_k } = ({\mathbf r}{L_{r-1},L_r}) \circ \cdots
({\mathbf r}{L_2,L_r}\circ \cdots \circ {\mathbf r}{L_2,L_3}) \circ
({\mathbf r}{L_1,L_r} \circ \cdots \circ {\mathbf r}{L_1,L_2}) \\ &
\colon \; q^{\sum_{1 \leqslant i < k \leqslant r}
\Lambda(L_i,L_k)} L_1 \circ \cdots \circ L_r \rightarrow L_r \circ \cdots \circ L_1
\quad \text{does not vanish.} \end{align*}
\begin{align*} {\mathbf r}{\underline{L}} &
\mathbin{:=} \prod_{1 \leqslant i < k \leqslant r}
{\mathbf r}{L_i,L_k } = ({\mathbf r}{L_{r-1},L_r}) \circ \cdots
({\mathbf r}{L_2,L_r}\circ \cdots \circ {\mathbf r}{L_2,L_3}) \circ
({\mathbf r}{L_1,L_r} \circ \cdots \circ {\mathbf r}{L_1,L_2}) \\ &
\colon \; q^{\sum_{1 \leqslant i < k \leqslant r}
\Lambda(L_i,L_k)} L_1 \circ \cdots \circ L_r \rightarrow L_r \circ \cdots \circ L_1
\quad \text{does not vanish.} \end{align*}
Lemma 2.10 [Reference Kashiwara and KimKK19, § 2.3] and [Reference Kashiwara, Kim, Oh and ParkKKOP23, § 2.2]
Let ![]() $\underline {L}$ be an almost affreal sequence of simple modules. If
$\underline {L}$ be an almost affreal sequence of simple modules. If ![]() $\underline {L}$ is normal, then the image of
$\underline {L}$ is normal, then the image of ![]() ${\mathbf r}{\underline {L}}$ is simple and coincides with the head of
${\mathbf r}{\underline {L}}$ is simple and coincides with the head of ![]() $L_1 \circ \cdots \circ L_r$ and also with the socle of
$L_1 \circ \cdots \circ L_r$ and also with the socle of ![]() $L_r \circ \cdots \circ L_1$, up to grading shifts.
$L_r \circ \cdots \circ L_1$, up to grading shifts.
Lemma 2.11 [Reference Kang, Kashiwara, Kim and OhKKKO18, Proposition 3.2.13]
Let ![]() $(A,B,C)$ be an almost affreal sequence. Then we have the following:
$(A,B,C)$ be an almost affreal sequence. Then we have the following:
(i)
 $\Lambda (A,B\triangledown C) =\Lambda (A,B)+\Lambda (A,C)$ if
$\Lambda (A,B\triangledown C) =\Lambda (A,B)+\Lambda (A,C)$ if  $A$ and
$A$ and  $B$ commute;
$B$ commute;(ii)
 $\Lambda (A\triangledown B, C) =\Lambda (A,C)+\Lambda (B,C)$ if
$\Lambda (A\triangledown B, C) =\Lambda (A,C)+\Lambda (B,C)$ if  $B$ and
$B$ and  $C$ commute.
$C$ commute.
For a given almost affreal sequence ![]() $\underline {L}$ of
$\underline {L}$ of ![]() $R$-modules, the sufficient conditions for
$R$-modules, the sufficient conditions for ![]() $\underline {L}$ being normal are studied in [Reference Kashiwara and KimKK19, Reference Kashiwara, Kim, Oh and ParkKKOP23]. In this paper, we will use the conditions frequently.
$\underline {L}$ being normal are studied in [Reference Kashiwara and KimKK19, Reference Kashiwara, Kim, Oh and ParkKKOP23]. In this paper, we will use the conditions frequently.
2.5 Commuting families
Let ![]() $J$ be an index set. We say that a family of affreal simple modules
$J$ be an index set. We say that a family of affreal simple modules ![]() $\mathcal {M}= \{ M_j \}_{j \in J}$ in
$\mathcal {M}= \{ M_j \}_{j \in J}$ in ![]() $R\text {-}\mathrm {gmod}$ is a commuting family if
$R\text {-}\mathrm {gmod}$ is a commuting family if
For a commuting family ![]() $\mathcal {M}= \{ M_j \ | \ j \in J\}$ in
$\mathcal {M}= \{ M_j \ | \ j \in J\}$ in ![]() $R\text {-}\mathrm {gmod}$, let us take
$R\text {-}\mathrm {gmod}$, let us take ![]() ${\mathbf \lambda} \colon \mathbb {Z}\mspace {1mu}^{\oplus J} \times \mathbb {Z}\mspace {1mu}^{\oplus J} \to \mathbb {Z}\mspace {1mu}$ such that
${\mathbf \lambda} \colon \mathbb {Z}\mspace {1mu}^{\oplus J} \times \mathbb {Z}\mspace {1mu}^{\oplus J} \to \mathbb {Z}\mspace {1mu}$ such that
Here ![]() $\{ \mathbf {e}_j \mid j \in J\}$ is the standard basis of
$\{ \mathbf {e}_j \mid j \in J\}$ is the standard basis of ![]() $\mathbb {Z}\mspace {1mu}^{\oplus J}$. Then there exists a family
$\mathbb {Z}\mspace {1mu}^{\oplus J}$. Then there exists a family ![]() $\{ \mathcal {M}_{\mathbf \lambda} (\mathbf {a}) \mid \mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{\oplus J}\}$ of simple modules in
$\{ \mathcal {M}_{\mathbf \lambda} (\mathbf {a}) \mid \mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{\oplus J}\}$ of simple modules in ![]() $\mathscr {C}_w$ such that
$\mathscr {C}_w$ such that
We sometimes omit ![]() $_{\mathbf \lambda}$ for notational simplicity.
$_{\mathbf \lambda}$ for notational simplicity.
Remark 2.12 Note that ![]() ${\mathbf \lambda} (\mathbf {e}_i,\mathbf {e}_j)=\widetilde {\Lambda }(M_i,M_j)$ satisfies condition (2.4). Moreover, if all the
${\mathbf \lambda} (\mathbf {e}_i,\mathbf {e}_j)=\widetilde {\Lambda }(M_i,M_j)$ satisfies condition (2.4). Moreover, if all the ![]() $M_i$ are self-dual, then
$M_i$ are self-dual, then ![]() $\mathcal {M}_{\mathbf \lambda} (\mathbf {a})$ is self-dual for any
$\mathcal {M}_{\mathbf \lambda} (\mathbf {a})$ is self-dual for any ![]() $\mathbf {a}\in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$. We usually take this choice of
$\mathbf {a}\in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$. We usually take this choice of ![]() ${\mathbf \lambda}$.
${\mathbf \lambda}$.
Definition 2.13 A commuting family ![]() $\mathcal {M}=\{ M_j \mid j \in J\}$ is called independent if
$\mathcal {M}=\{ M_j \mid j \in J\}$ is called independent if ![]() $\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{\oplus J}$ satisfies
$\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{\oplus J}$ satisfies ![]() $\mathcal {M}(\mathbf {a}) \simeq q^s \mathcal {M}(\mathbf {b})$ for some
$\mathcal {M}(\mathbf {a}) \simeq q^s \mathcal {M}(\mathbf {b})$ for some ![]() $s \in \mathbb {Z}\mspace {1mu}$, then we have
$s \in \mathbb {Z}\mspace {1mu}$, then we have ![]() $\mathbf {a}=\mathbf {b}$.
$\mathbf {a}=\mathbf {b}$.
The following lemma is obvious.
Lemma 2.14 Let ![]() $\mathcal {M} = \{ M_j \mid j \in J \}$ be a commuting family. Then it is independent if and only if the set
$\mathcal {M} = \{ M_j \mid j \in J \}$ be a commuting family. Then it is independent if and only if the set ![]() $\big \{ \big [ \mathcal {M}(\mathbf {a})\big ] \mid \mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{\oplus J} \big \}$ in
$\big \{ \big [ \mathcal {M}(\mathbf {a})\big ] \mid \mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{\oplus J} \big \}$ in ![]() $K(R\text {-}\mathrm {gmod})$ is linearly independent over
$K(R\text {-}\mathrm {gmod})$ is linearly independent over ![]() $\mathbb {Z}\mspace {1mu}[q^{\pm 1}]$.
$\mathbb {Z}\mspace {1mu}[q^{\pm 1}]$.
2.6 Localization of  $\mathscr {C}_w$
$\mathscr {C}_w$
Throughout this subsection, we fix ![]() $w \in \mathsf {W}$ and set
$w \in \mathsf {W}$ and set
For notational simplicity, let us write
Then ![]() $\{ \Omega ([C_i]) \mid i \in I_w\}$ forms the set of frozen variables of
$\{ \Omega ([C_i]) \mid i \in I_w\}$ forms the set of frozen variables of ![]() $\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$. For each
$\mathcal {A}_\mathbb {A}(\mathfrak {n}(w))$. For each ![]() $\mu = \sum _{i \in I} \mu _i\varpi _i \in \mathsf {P}^+$, we set
$\mu = \sum _{i \in I} \mu _i\varpi _i \in \mathsf {P}^+$, we set ![]() $C_\mu = M(w\mu,\mu )$, which is a self-dual convolution product
$C_\mu = M(w\mu,\mu )$, which is a self-dual convolution product ![]() $q^c \circ _{i \in I} C_i^{\circ \mu _i}$ for some
$q^c \circ _{i \in I} C_i^{\circ \mu _i}$ for some ![]() $c\in \mathbb {Z}\mspace {1mu}$.
$c\in \mathbb {Z}\mspace {1mu}$.
It is proved in [Reference Kashiwara, Kim, Oh and ParkKKOP21, Reference Kashiwara, Kim, Oh and ParkKKOP23, Reference Kashiwara, Kim, Oh and ParkKKOP24a] that there exists a monoidal abelian category ![]() $\widetilde {\mathscr {C}}_w = \mathscr {C}_w[C_i^{\circ -1} \mid i \in I]$ with a tensor product
$\widetilde {\mathscr {C}}_w = \mathscr {C}_w[C_i^{\circ -1} \mid i \in I]$ with a tensor product ![]() $\circ$, a degree shift functor
$\circ$, a degree shift functor ![]() $q$ and a monoidal exact fully faithful functor
$q$ and a monoidal exact fully faithful functor ![]() $\Phi _w\colon \mathscr {C}_w \to \widetilde {\mathscr {C}}_w$ satisfying the following properties.
$\Phi _w\colon \mathscr {C}_w \to \widetilde {\mathscr {C}}_w$ satisfying the following properties.

(For the precise properties, see [Reference Kashiwara, Kim, Oh and ParkKKOP21, Reference Kashiwara, Kim, Oh and ParkKKOP23, Reference Kashiwara, Kim, Oh and ParkKKOP24a].)
Theorem 2.15 ([Reference Kashiwara, Kim, Oh and ParkKKOP21] (see also [Reference Kashiwara, Kim, Oh and ParkKKOP23, Remark 3.6]))
There exists an ![]() $\mathbb {A}$-algebra isomorphism
$\mathbb {A}$-algebra isomorphism
Here ![]() $K(\widetilde {\mathscr {C}}_w)$ denotes the Grothendieck ring of
$K(\widetilde {\mathscr {C}}_w)$ denotes the Grothendieck ring of ![]() $\widetilde {\mathscr {C}}_w$.
$\widetilde {\mathscr {C}}_w$.
A pair ![]() $(\varepsilon \colon X \otimes Y \to \mathbf {1}, \; \eta \colon \mathbf {1} \to Y \otimes X)$ of morphisms in a monoidal category with a unit object
$(\varepsilon \colon X \otimes Y \to \mathbf {1}, \; \eta \colon \mathbf {1} \to Y \otimes X)$ of morphisms in a monoidal category with a unit object ![]() $\mathbf {1}$ is called an adjunction if the following two conditions hold.
$\mathbf {1}$ is called an adjunction if the following two conditions hold.
(a) The composition
 $X \simeq X \otimes \mathbf {1} \mathop\longrightarrow\limits^{[X \otimes \eta]} X \otimes Y \otimes X \mathop\longrightarrow\limits^{[\varepsilon \otimes X]} \mathbf {1} \otimes X \simeq X$ is the identity.
$X \simeq X \otimes \mathbf {1} \mathop\longrightarrow\limits^{[X \otimes \eta]} X \otimes Y \otimes X \mathop\longrightarrow\limits^{[\varepsilon \otimes X]} \mathbf {1} \otimes X \simeq X$ is the identity.(b) The composition
 $Y \simeq \mathbf {1} \otimes Y \mathop\longrightarrow\limits^{[\eta \otimes Y]} Y \otimes X \otimes Y \mathop\longrightarrow\limits^{[Y \otimes \varepsilon]} Y \otimes \mathbf {1} \simeq Y$ is the identity.
$Y \simeq \mathbf {1} \otimes Y \mathop\longrightarrow\limits^{[\eta \otimes Y]} Y \otimes X \otimes Y \mathop\longrightarrow\limits^{[Y \otimes \varepsilon]} Y \otimes \mathbf {1} \simeq Y$ is the identity.
In the case when ![]() $(\varepsilon,\eta )$ is an adjunction, we say that
$(\varepsilon,\eta )$ is an adjunction, we say that ![]() $X$ is a left dual to
$X$ is a left dual to ![]() $Y$,
$Y$, ![]() $Y$ is a right dual to
$Y$ is a right dual to ![]() $X$ and
$X$ and ![]() $(X,Y)$ is a dual pair.
$(X,Y)$ is a dual pair.
Theorem 2.16 [Reference Kashiwara, Kim, Oh and ParkKKOP21, Reference Kashiwara, Kim, Oh and ParkKKOP23]
The monoidal category ![]() $\widetilde {\mathscr {C}}_w$ is rigid; i.e. every object of
$\widetilde {\mathscr {C}}_w$ is rigid; i.e. every object of ![]() $\widetilde {\mathscr {C}}_w$ has a right dual and a left dual in
$\widetilde {\mathscr {C}}_w$ has a right dual and a left dual in ![]() $\widetilde {\mathscr {C}}_w$.
$\widetilde {\mathscr {C}}_w$.
2.7 Determinantal modules and monoidal clusters
In this subsection, we denote by ![]() $\mathcal {C}$ the category of
$\mathcal {C}$ the category of ![]() $\mathscr {C}_w$ or
$\mathscr {C}_w$ or ![]() $\widetilde {\mathscr {C}}_w$. Recall that
$\widetilde {\mathscr {C}}_w$. Recall that
Let ![]() ${\boldsymbol {i}}=(i_1,\ldots,i_r)$ be a reduced sequence of
${\boldsymbol {i}}=(i_1,\ldots,i_r)$ be a reduced sequence of ![]() $w \in \mathsf {W}$. For
$w \in \mathsf {W}$. For ![]() $k$ such that
$k$ such that ![]() $1\leqslant k\leqslant r$, set
$1\leqslant k\leqslant r$, set
(see Proposition 2.2 for the notation).
Proposition 2.17 [Reference Kashiwara, Kim, Oh and ParkKKOP18, Theorem 4.12]
Let ![]() ${\boldsymbol {i}}=(i_1,\ldots,i_r)$ be a reduced sequence of
${\boldsymbol {i}}=(i_1,\ldots,i_r)$ be a reduced sequence of ![]() $w \in \mathsf {W}$. For
$w \in \mathsf {W}$. For ![]() $s < t \in \mathsf {K}$, we have
$s < t \in \mathsf {K}$, we have
We say that a commuting family ![]() $\mathcal {M}=\{M_i\}_{i\in \mathsf {K}}$ in
$\mathcal {M}=\{M_i\}_{i\in \mathsf {K}}$ in ![]() $\mathcal {C}$ is a monoidal cluster if there exists a quantum seed
$\mathcal {C}$ is a monoidal cluster if there exists a quantum seed ![]() $(\{ X_i \}_{i \in \mathsf {K}}, L=(l_{i,j})_{i,j \in \mathsf {K}}, \widetilde {B}=(b_{i,j})_{i \in \mathsf {K},j\in {\mathsf {K}_\mathrm {ex}}} )$ of
$(\{ X_i \}_{i \in \mathsf {K}}, L=(l_{i,j})_{i,j \in \mathsf {K}}, \widetilde {B}=(b_{i,j})_{i \in \mathsf {K},j\in {\mathsf {K}_\mathrm {ex}}} )$ of ![]() $\mathscr {A}$ such that
$\mathscr {A}$ such that
Note that every monoidal seed is independent since the quantum cluster monomials in a cluster are linearly independent over ![]() $\mathbb {A}$ by the definition.
$\mathbb {A}$ by the definition.
With Proposition 2.2 and (2.2), Proposition 2.17 says that
for any reduced sequence ![]() ${\boldsymbol {i}}=(i_1,\ldots,i_r)$ of
${\boldsymbol {i}}=(i_1,\ldots,i_r)$ of ![]() $w$. We call
$w$. We call ![]() $\mathcal {M}^{\boldsymbol {i}}$ the GLS cluster (associated with
$\mathcal {M}^{\boldsymbol {i}}$ the GLS cluster (associated with ![]() ${\boldsymbol {i}}$).
${\boldsymbol {i}}$).
3. Quasi-Laurent family and Laurent family
In this section, we introduce the notions of quasi-Laurent families and Laurent families, which allow us to associate two vectors in ![]() $\mathbb {Z}\mspace {1mu}^{J}$ with each simple module.
$\mathbb {Z}\mspace {1mu}^{J}$ with each simple module.
3.1 Definition
Let ![]() $J$ be a finite index set. Let
$J$ be a finite index set. Let ![]() $\mathscr {C}$ be a full monoidal subcategory of
$\mathscr {C}$ be a full monoidal subcategory of ![]() $R\text {-}\mathrm {gmod}$ stable by taking subquotients, extensions and grading shifts.
$R\text {-}\mathrm {gmod}$ stable by taking subquotients, extensions and grading shifts.
Lemma 3.1 Let ![]() $\mathcal {M}=\{ M_j \mid j \in J\}$ be an independent commuting family of affreal simple objects in
$\mathcal {M}=\{ M_j \mid j \in J\}$ be an independent commuting family of affreal simple objects in ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $X$ a simple module in
$X$ a simple module in ![]() $\mathscr {C}$.
$\mathscr {C}$.
(i) If
 $\mathbf {a}$,
$\mathbf {a}$,  $\mathbf {a}'$,
$\mathbf {a}'$,  $\mathbf {b}$,
$\mathbf {b}$,  $\mathbf {b}'\in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ satisfy
$\mathbf {b}'\in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ satisfy  $X \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$ and
$X \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$ and  $X \triangledown \mathcal {M}(\mathbf {a}') \simeq \mathcal {M}(\mathbf {b}')$ up to grading shifts, then one has
$X \triangledown \mathcal {M}(\mathbf {a}') \simeq \mathcal {M}(\mathbf {b}')$ up to grading shifts, then one has  $\mathbf {b}-\mathbf {a}=\mathbf {b}'-\mathbf {a}'$.
$\mathbf {b}-\mathbf {a}=\mathbf {b}'-\mathbf {a}'$.(ii) If
 $\mathbf {a}$,
$\mathbf {a}$,  $\mathbf {a}'$,
$\mathbf {a}'$,  $\mathbf {b}$,
$\mathbf {b}$,  $\mathbf {b}'\in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ satisfy
$\mathbf {b}'\in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ satisfy  $\mathcal {M}(\mathbf {a}) \triangledown X \simeq \mathcal {M}(\mathbf {b})$ and
$\mathcal {M}(\mathbf {a}) \triangledown X \simeq \mathcal {M}(\mathbf {b})$ and  $\mathcal {M}(\mathbf {a}') \triangledown X \simeq \mathcal {M}(\mathbf {b}')$ up to grading shifts, then one has
$\mathcal {M}(\mathbf {a}') \triangledown X \simeq \mathcal {M}(\mathbf {b}')$ up to grading shifts, then one has  $\mathbf {b}-\mathbf {a}=\mathbf {b}'-\mathbf {a}'$.
$\mathbf {b}-\mathbf {a}=\mathbf {b}'-\mathbf {a}'$.
Proof. Since the proof are similar, we prove only part (i). We have
 \begin{align*} \mathcal{M}(\mathbf{b}+\mathbf{a}') \simeq \mathcal{M}(\mathbf{b}) \triangledown \mathcal{M}(\mathbf{a}') &\simeq( X \triangledown \mathcal{M}(\mathbf{a}) ) \triangledown \mathcal{M}(\mathbf{a}') \simeq {\operatorname{hd}}(X \circ \mathcal{M}(\mathbf{a}') \circ \mathcal{M}(\mathbf{a}) )\\ &\simeq( X \triangledown \mathcal{M}(\mathbf{a}') ) \triangledown \mathcal{M}(\mathbf{a}) \simeq \mathcal{M}(\mathbf{b}'+\mathbf{a}), \end{align*}
\begin{align*} \mathcal{M}(\mathbf{b}+\mathbf{a}') \simeq \mathcal{M}(\mathbf{b}) \triangledown \mathcal{M}(\mathbf{a}') &\simeq( X \triangledown \mathcal{M}(\mathbf{a}) ) \triangledown \mathcal{M}(\mathbf{a}') \simeq {\operatorname{hd}}(X \circ \mathcal{M}(\mathbf{a}') \circ \mathcal{M}(\mathbf{a}) )\\ &\simeq( X \triangledown \mathcal{M}(\mathbf{a}') ) \triangledown \mathcal{M}(\mathbf{a}) \simeq \mathcal{M}(\mathbf{b}'+\mathbf{a}), \end{align*}
and, hence, we have ![]() $\mathbf {a}'+\mathbf {b}=\mathbf {a}+\mathbf {b}'$ since
$\mathbf {a}'+\mathbf {b}=\mathbf {a}+\mathbf {b}'$ since ![]() $\mathcal {M}$ is independent.
$\mathcal {M}$ is independent.
Definition 3.2 We say that a commuting family ![]() $\mathcal {M}= \{ M_j \mid j \in J \}$ of affreal simple objects of
$\mathcal {M}= \{ M_j \mid j \in J \}$ of affreal simple objects of ![]() $\mathscr {C}$ is a quasi-Laurent family in
$\mathscr {C}$ is a quasi-Laurent family in ![]() $\mathscr {C}$ if
$\mathscr {C}$ if ![]() $\mathcal {M}$ satisfies the following conditions:
$\mathcal {M}$ satisfies the following conditions:
(a)
 $\mathcal {M}$ is independent; and
$\mathcal {M}$ is independent; and(b) if a simple module
 $X$ commutes with all
$X$ commutes with all  $M_j$
$M_j$  $(j \in J)$, then there exist
$(j \in J)$, then there exist  $\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ such that
$\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ such that
 \[ X \circ \mathcal{M}(\mathbf{a}) \simeq \mathcal{M}(\mathbf{b})\quad\text{up to a grading shift}. \]
\[ X \circ \mathcal{M}(\mathbf{a}) \simeq \mathcal{M}(\mathbf{b})\quad\text{up to a grading shift}. \]
If ![]() $\mathcal {M}$ satisfies part (a) and part (c) below, then we say that
$\mathcal {M}$ satisfies part (a) and part (c) below, then we say that ![]() $\mathcal {M}$ is a Laurent family:
$\mathcal {M}$ is a Laurent family:
(c) if a simple module
 $X$ commutes with all
$X$ commutes with all  $M_j$
$M_j$  $(j \in J)$, then there exists
$(j \in J)$, then there exists  $\mathbf {b}\in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ such that
$\mathbf {b}\in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ such that  $X\simeq \mathcal {M}(\mathbf {b})$.
$X\simeq \mathcal {M}(\mathbf {b})$.
Note that a Laurent family is a quasi-Laurent family.
Lemma 3.3 Let ![]() $\mathcal {M} = \{ M_j \mid j \in J\}$ be a quasi-Laurent family in
$\mathcal {M} = \{ M_j \mid j \in J\}$ be a quasi-Laurent family in ![]() $\mathscr {C}$. Then we have the following:
$\mathscr {C}$. Then we have the following:
(i) for any simple module
 $X \in \mathscr {C}$, there exist
$X \in \mathscr {C}$, there exist  $\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}^J_{\geqslant 0}$ such that
$\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}^J_{\geqslant 0}$ such that  $X \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$ up to a grading shift;
$X \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$ up to a grading shift;(ii) for any simple module
 $X \in \mathscr {C}$, there exist
$X \in \mathscr {C}$, there exist  $\mathbf {a}',\mathbf {b}' \in \mathbb {Z}\mspace {1mu}^J_{\geqslant 0}$ such that
$\mathbf {a}',\mathbf {b}' \in \mathbb {Z}\mspace {1mu}^J_{\geqslant 0}$ such that  $X \triangle \mathcal {M}(\mathbf {a}') \simeq \mathcal {M}(\mathbf {b}')$ up to a grading shift.
$X \triangle \mathcal {M}(\mathbf {a}') \simeq \mathcal {M}(\mathbf {b}')$ up to a grading shift.
Proof. Since the proofs are similar, we shall only prove the first statement. Let us take ![]() $\mathbf {a}^{(1)} \in \mathbb {Z}\mspace {1mu}^J_{\geqslant 0}$ such that
$\mathbf {a}^{(1)} \in \mathbb {Z}\mspace {1mu}^J_{\geqslant 0}$ such that ![]() $\mathbf {a}^{(1)}_j \gg 0$ for all
$\mathbf {a}^{(1)}_j \gg 0$ for all ![]() $j \in J$. Then Proposition 2.8 says that the simple module
$j \in J$. Then Proposition 2.8 says that the simple module ![]() $Y \mathbin {:=} X \triangledown \mathcal {M}(\mathbf {a}^{(1)})$ commutes with all
$Y \mathbin {:=} X \triangledown \mathcal {M}(\mathbf {a}^{(1)})$ commutes with all ![]() $M_j$. Since
$M_j$. Since ![]() $\mathcal {M}$ is a quasi-Laurent family, there exists
$\mathcal {M}$ is a quasi-Laurent family, there exists ![]() $\mathbf {a}^{(2)},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^J$ such that
$\mathbf {a}^{(2)},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^J$ such that ![]() $Y \circ \mathcal {M}(\mathbf {a}^{(2)}) \simeq \mathcal {M}(\mathbf {b})$. Hence, by taking
$Y \circ \mathcal {M}(\mathbf {a}^{(2)}) \simeq \mathcal {M}(\mathbf {b})$. Hence, by taking ![]() $\mathbf {a} = \mathbf {a}^{(1)}+\mathbf {a}^{(2)}$, we have
$\mathbf {a} = \mathbf {a}^{(1)}+\mathbf {a}^{(2)}$, we have
as desired.
By applying the similar argument as in the lemma above to composition factors of ![]() $X \circ \mathcal {M}(\mathbf {a})$, we have the following corollary.
$X \circ \mathcal {M}(\mathbf {a})$, we have the following corollary.
Corollary 3.4 Let ![]() $\mathcal {M}$ be a quasi-Laurent family in
$\mathcal {M}$ be a quasi-Laurent family in ![]() $\mathscr {C}$. Then, for any
$\mathscr {C}$. Then, for any ![]() $X\in \mathscr {C}$, there exist
$X\in \mathscr {C}$, there exist ![]() $\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}$, a finite index set
$\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}$, a finite index set ![]() $\mathsf {S}$,
$\mathsf {S}$, ![]() $c(s) \in \mathbb {Z}\mspace {1mu}$ and
$c(s) \in \mathbb {Z}\mspace {1mu}$ and ![]() $\mathbf {b}(s) \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^J$
$\mathbf {b}(s) \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^J$ ![]() $(s \in \mathsf {S})$ such that
$(s \in \mathsf {S})$ such that
Remark 3.5 The above corollary says that for every module ![]() $X$ in
$X$ in ![]() $\mathscr {C}$ and a quasi-Laurent family
$\mathscr {C}$ and a quasi-Laurent family ![]() $\mathcal {M} = \{ M_j \mid j \in J\}$, the isomorphism class
$\mathcal {M} = \{ M_j \mid j \in J\}$, the isomorphism class ![]() $[X]$ of
$[X]$ of ![]() $X$ in
$X$ in ![]() $K(\mathscr {C})$ can be expressed as an element in the Laurent polynomial ring
$K(\mathscr {C})$ can be expressed as an element in the Laurent polynomial ring ![]() $\mathbb {Z}\mspace {1mu}[q^{\pm 1}][[M_j]^{\pm 1} \mid j \in J]$ with positive coefficients.
$\mathbb {Z}\mspace {1mu}[q^{\pm 1}][[M_j]^{\pm 1} \mid j \in J]$ with positive coefficients.
Proposition 3.6 Assume that ![]() $\mathcal {K}_\mathbb {A}(\mathscr {C})$ has a quantum cluster algebra structure, and let
$\mathcal {K}_\mathbb {A}(\mathscr {C})$ has a quantum cluster algebra structure, and let ![]() $\mathcal {M}=\{ M_k \mid k\in \mathsf {K}\}$ be a monoidal cluster in
$\mathcal {M}=\{ M_k \mid k\in \mathsf {K}\}$ be a monoidal cluster in ![]() $\mathscr {C}$. Then the commuting family
$\mathscr {C}$. Then the commuting family ![]() $\mathcal {M}$ is a quasi-Laurent family. In particular, the isomorphism class
$\mathcal {M}$ is a quasi-Laurent family. In particular, the isomorphism class ![]() $[X]$ of
$[X]$ of ![]() $X$ in
$X$ in ![]() $K(\mathscr {C})$ can be expressed as an element in the Laurent polynomial
$K(\mathscr {C})$ can be expressed as an element in the Laurent polynomial ![]() $\mathbb {Z}\mspace {1mu}[q^{\pm 1}][\;[M_j] \mid j \in J]$ with positive coefficients.
$\mathbb {Z}\mspace {1mu}[q^{\pm 1}][\;[M_j] \mid j \in J]$ with positive coefficients.
If, moreover, every ![]() $[M_k]$ is prime in
$[M_k]$ is prime in ![]() $K(\mathscr {C})\vert _{q=1}$, then
$K(\mathscr {C})\vert _{q=1}$, then ![]() $\mathcal {M}$ is a Laurent family.
$\mathcal {M}$ is a Laurent family.
Note that if ![]() $K(\mathscr {C})\vert _{q=1}$ is factorial, then every
$K(\mathscr {C})\vert _{q=1}$ is factorial, then every ![]() $[M_k]$ is prime in
$[M_k]$ is prime in ![]() $K(\mathscr {C})\vert _{q=1}$ (see [Reference Geiss, Leclerc and SchröerGLS13b]).
$K(\mathscr {C})\vert _{q=1}$ (see [Reference Geiss, Leclerc and SchröerGLS13b]).
Proof. Let ![]() $X$ be a simple module in
$X$ be a simple module in ![]() $\mathscr {C}$ commuting with all
$\mathscr {C}$ commuting with all ![]() $M_k$
$M_k$ ![]() $(k\in \mathsf {K})$. The quantum Laurent phenomenon states that there exists
$(k\in \mathsf {K})$. The quantum Laurent phenomenon states that there exists ![]() $\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$ such that
$\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$ such that
 \begin{equation} [X] = \dfrac{\sum_{s \in \mathsf{S}} c(s)[\mathcal{M}(\mathbf{b}^{(s)})]}{[\mathcal{M}(\mathbf{a})]} \iff [X \circ \mathcal{M}(\mathbf{a})] = \sum_{s \in \mathsf{S}} c(s)[\mathcal{M}(\mathbf{b}^{(s)})] \end{equation}
\begin{equation} [X] = \dfrac{\sum_{s \in \mathsf{S}} c(s)[\mathcal{M}(\mathbf{b}^{(s)})]}{[\mathcal{M}(\mathbf{a})]} \iff [X \circ \mathcal{M}(\mathbf{a})] = \sum_{s \in \mathsf{S}} c(s)[\mathcal{M}(\mathbf{b}^{(s)})] \end{equation}
for some ![]() $\ell \in \mathbb {Z}\mspace {1mu}_{\geqslant 1}$,
$\ell \in \mathbb {Z}\mspace {1mu}_{\geqslant 1}$, ![]() $\mathbf {b}^{(s)} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$ and
$\mathbf {b}^{(s)} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$ and ![]() $c(s) \in \mathbb {Z}\mspace {1mu}[q^{\pm 1/2}]$. Since
$c(s) \in \mathbb {Z}\mspace {1mu}[q^{\pm 1/2}]$. Since ![]() $X \circ \mathcal {M}(\mathbf {a})$ is simple, the right-hand side of (3.2) must coincide with
$X \circ \mathcal {M}(\mathbf {a})$ is simple, the right-hand side of (3.2) must coincide with ![]() $q^c\mathcal {M}(\mathbf {c})$ for some
$q^c\mathcal {M}(\mathbf {c})$ for some ![]() $\mathbf {c} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^J$ and
$\mathbf {c} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^J$ and ![]() $c \in \mathbb {Z}\mspace {1mu}$. Hence,
$c \in \mathbb {Z}\mspace {1mu}$. Hence, ![]() $\mathcal{M}$ is a quasi-Laurent family.
$\mathcal{M}$ is a quasi-Laurent family.
Let us show that ![]() $\mathcal {M}$ is a Laurent family. If
$\mathcal {M}$ is a Laurent family. If ![]() $X\circ \mathcal {M}(\mathbf {a})\simeq \mathcal {M}(\mathbf {b})$, then we have
$X\circ \mathcal {M}(\mathbf {a})\simeq \mathcal {M}(\mathbf {b})$, then we have ![]() $\mathbf {a}_k\leqslant \mathbf {b}_k$ for all
$\mathbf {a}_k\leqslant \mathbf {b}_k$ for all ![]() $k$, since each
$k$, since each ![]() $[M_k]$ is a prime element of
$[M_k]$ is a prime element of ![]() $K(\mathscr {C})\vert _{q=1}$. Hence, setting
$K(\mathscr {C})\vert _{q=1}$. Hence, setting ![]() $\mathbf {c}=\mathbf {b}-\mathbf {a}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K}$, we have
$\mathbf {c}=\mathbf {b}-\mathbf {a}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K}$, we have ![]() $X\circ \mathcal {M}(\mathbf {a})\simeq \mathcal {M}(\mathbf {c})\circ \mathcal {M}(\mathbf {a})$, which implies that
$X\circ \mathcal {M}(\mathbf {a})\simeq \mathcal {M}(\mathbf {c})\circ \mathcal {M}(\mathbf {a})$, which implies that ![]() $X\simeq \mathcal {M}(\mathbf {c})$. Hence,
$X\simeq \mathcal {M}(\mathbf {c})$. Hence, ![]() $\mathcal {M}$ is a Laurent family.
$\mathcal {M}$ is a Laurent family.
Definition 3.7 For a simple module ![]() $X \in \mathscr {C}$ and a quasi-Laurent family
$X \in \mathscr {C}$ and a quasi-Laurent family ![]() $\mathcal {M}=\{ M_j \mid j \in J \}$, take
$\mathcal {M}=\{ M_j \mid j \in J \}$, take ![]() $\mathbf {a},\mathbf {b},\mathbf {a}',\mathbf {b}' \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^J$ such that
$\mathbf {a},\mathbf {b},\mathbf {a}',\mathbf {b}' \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^J$ such that ![]() $X \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$ and
$X \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$ and ![]() $X \triangle \mathcal {M}(\mathbf {a}') \simeq \mathcal {M}(\mathbf {b}')$ up to grading shifts. Then we define
$X \triangle \mathcal {M}(\mathbf {a}') \simeq \mathcal {M}(\mathbf {b}')$ up to grading shifts. Then we define
Remark 3.8
(1) For a quasi-Laurent family
 $\mathcal {M}$ in
$\mathcal {M}$ in  $\mathscr {C}$,
$\mathscr {C}$,  $\mathbf {g}_\mathcal {M}^R$ and
$\mathbf {g}_\mathcal {M}^R$ and  $\mathbf {g}_\mathcal {M}^L$ are well-defined by Lemma 3.1.
$\mathbf {g}_\mathcal {M}^L$ are well-defined by Lemma 3.1.(2) For a reduced sequence
 ${\boldsymbol {i}}$ of
${\boldsymbol {i}}$ of  $w$ and its quasi-Laurent family
$w$ and its quasi-Laurent family  $\mathcal {M}^{\boldsymbol {i}}$, we write
$\mathcal {M}^{\boldsymbol {i}}$, we write  $\mathbf {g}_{\boldsymbol {i}}^R$ and
$\mathbf {g}_{\boldsymbol {i}}^R$ and  $\mathbf {g}_{\boldsymbol {i}}^L$ instead of
$\mathbf {g}_{\boldsymbol {i}}^L$ instead of  $\mathbf {g}_{\mathcal {M}^{\boldsymbol {i}}}^R$ and
$\mathbf {g}_{\mathcal {M}^{\boldsymbol {i}}}^R$ and  $\mathbf {g}_{\mathcal {M}^{\boldsymbol {i}}}^L$, respectively.
$\mathbf {g}_{\mathcal {M}^{\boldsymbol {i}}}^L$, respectively.(3) The map
 $\mathbf {g}_{\boldsymbol {i}}^R$ and
$\mathbf {g}_{\boldsymbol {i}}^R$ and  $\mathbf {g}_{\boldsymbol {i}}^L$ for the quasi-Laurent family
$\mathbf {g}_{\boldsymbol {i}}^L$ for the quasi-Laurent family  $\mathcal {M}^{\boldsymbol {i}}$ can be extended to the set
$\mathcal {M}^{\boldsymbol {i}}$ can be extended to the set  ${\rm Irr}(\widetilde {\mathscr {C}}_w)$ of the isomorphism classes of self-dual simples in
${\rm Irr}(\widetilde {\mathscr {C}}_w)$ of the isomorphism classes of self-dual simples in  $\widetilde {\mathscr {C}}_w$.
$\widetilde {\mathscr {C}}_w$.
The following lemma can be proved by the same arguments in [Reference Kashiwara and KimKK19].
Lemma 3.9 Let ![]() $\mathcal {M}$ be a quasi-Laurent family in
$\mathcal {M}$ be a quasi-Laurent family in ![]() $\mathscr {C}$ and
$\mathscr {C}$ and ![]() $X$ a simple module in
$X$ a simple module in ![]() $\mathscr {C}$.
$\mathscr {C}$.
(i) If
 $\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ satisfy
$\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ satisfy  $\mathbf {b}-\mathbf {a} = \mathbf {g}_\mathcal {M}^R(X)$
$\mathbf {b}-\mathbf {a} = \mathbf {g}_\mathcal {M}^R(X)$  $($respectively,
$($respectively,  $\mathbf {b}-\mathbf {a} = \mathbf {g}_\mathcal {M}^L(X))$, then we have
$\mathbf {b}-\mathbf {a} = \mathbf {g}_\mathcal {M}^L(X))$, then we have
 \[ {X \triangledown \mathcal{M}(\mathbf{a}) \simeq \mathcal{M}(\mathbf{b}) ({\textrm respectively}, X \triangle \mathcal{M}(\mathbf{a}) \simeq \mathcal{M}(\mathbf{b})) textrm {up to a grading shift}.} \]
\[ {X \triangledown \mathcal{M}(\mathbf{a}) \simeq \mathcal{M}(\mathbf{b}) ({\textrm respectively}, X \triangle \mathcal{M}(\mathbf{a}) \simeq \mathcal{M}(\mathbf{b})) textrm {up to a grading shift}.} \]
(ii) For any
 $\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$, we have
$\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$, we have
 \[ \mathbf{g}_\mathcal{M}^R(X \triangledown \mathcal{M}(\mathbf{a})) = \mathbf{g}_\mathcal{M}^R(X)+\mathbf{a} \quad \text{and}\quad \mathbf{g}_\mathcal{M}^L(X \triangle \mathcal{M}(\mathbf{a})) = \mathbf{g}_\mathcal{M}^L(X)+\mathbf{a}. \]
\[ \mathbf{g}_\mathcal{M}^R(X \triangledown \mathcal{M}(\mathbf{a})) = \mathbf{g}_\mathcal{M}^R(X)+\mathbf{a} \quad \text{and}\quad \mathbf{g}_\mathcal{M}^L(X \triangle \mathcal{M}(\mathbf{a})) = \mathbf{g}_\mathcal{M}^L(X)+\mathbf{a}. \]
(iii) The maps
 $\mathbf {g}_\mathcal {M}^R$ and
$\mathbf {g}_\mathcal {M}^R$ and  $\mathbf {g}_\mathcal {M}^L$ from
$\mathbf {g}_\mathcal {M}^L$ from  ${\rm Irr}(\mathscr {C})$ to
${\rm Irr}(\mathscr {C})$ to  $\mathbb {Z}\mspace {1mu}^{J}$ are injective.
$\mathbb {Z}\mspace {1mu}^{J}$ are injective.
4. PBW decomposition vector and GLS seed
In this section, we recall the PBW basis, and we investigate the relationship between the ![]() $g$-vectors and the PBW decomposition vectors.
$g$-vectors and the PBW decomposition vectors.
4.1 PBW decomposition vector
Let us take ![]() $w \in \mathsf {W}$ and its reduced sequence
$w \in \mathsf {W}$ and its reduced sequence ![]() ${\boldsymbol {i}}=(i_1,\ldots,i_r)$. Recall the following.
${\boldsymbol {i}}=(i_1,\ldots,i_r)$. Recall the following.
(a) We take an index set
 $\mathsf {K}=[1,r]$ with a decomposition
$\mathsf {K}=[1,r]$ with a decomposition
 \[ {\mathsf{K}_\mathrm{ex}} \sqcup {\mathsf{K}_\mathrm{fr}} \quad \text{where} \ {\mathsf{K}_\mathrm{ex}}=\{k\in\mathsf{K}\mid k_+\leqslant r\}. \]
\[ {\mathsf{K}_\mathrm{ex}} \sqcup {\mathsf{K}_\mathrm{fr}} \quad \text{where} \ {\mathsf{K}_\mathrm{ex}}=\{k\in\mathsf{K}\mid k_+\leqslant r\}. \]
(b) For each
 $1 \leqslant k \leqslant r$, we set
$1 \leqslant k \leqslant r$, we set  ${\mspace {1mu}\beta }^{\boldsymbol {i}}_k \in \Delta ^+ \cap w\Delta ^-$ and define simple modules
${\mspace {1mu}\beta }^{\boldsymbol {i}}_k \in \Delta ^+ \cap w\Delta ^-$ and define simple modules  $S^{\boldsymbol {i}}_k = M(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},w^{\boldsymbol {i}}_{< k}\varpi _{i_k})$ and
$S^{\boldsymbol {i}}_k = M(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},w^{\boldsymbol {i}}_{< k}\varpi _{i_k})$ and  $M^{\boldsymbol {i}}_k = M(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},\varpi _{i_k})$. Note that
(4.1)
$M^{\boldsymbol {i}}_k = M(w^{\boldsymbol {i}}_{\leqslant k}\varpi _{i_k},\varpi _{i_k})$. Note that
(4.1) \begin{equation} M^{\boldsymbol{i}}_k \simeq S^{\boldsymbol{i}}_k \triangledown M^{\boldsymbol{i}}_{k_-} \quad \text{and} \quad \mathcal{M}^{\boldsymbol{i}} \mathbin{:=} \{M_k^{\boldsymbol{i}}\mid k\in \mathsf{K}\} \text{ forms a commuting family.} \end{equation}
\begin{equation} M^{\boldsymbol{i}}_k \simeq S^{\boldsymbol{i}}_k \triangledown M^{\boldsymbol{i}}_{k_-} \quad \text{and} \quad \mathcal{M}^{\boldsymbol{i}} \mathbin{:=} \{M_k^{\boldsymbol{i}}\mid k\in \mathsf{K}\} \text{ forms a commuting family.} \end{equation}
For any ![]() $\mathbf {a} = (\mathbf {a}_k)_{1 \leqslant k \leqslant r} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$, the convolution product
$\mathbf {a} = (\mathbf {a}_k)_{1 \leqslant k \leqslant r} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$, the convolution product
has a self-dual simple head. Conversely, every self-dual simple module in ![]() $\mathscr {C}_w$ is isomorphic to
$\mathscr {C}_w$ is isomorphic to ![]() ${\operatorname {hd}}(P_{\boldsymbol {i}}(\mathbf {a}))$ for some
${\operatorname {hd}}(P_{\boldsymbol {i}}(\mathbf {a}))$ for some ![]() $\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K}$ in a unique way (see [Reference McNamaraMcN15, Theorem 3.1] and [Reference Tingley and WebsterTW16, Theorem 2.19]). We call
$\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K}$ in a unique way (see [Reference McNamaraMcN15, Theorem 3.1] and [Reference Tingley and WebsterTW16, Theorem 2.19]). We call ![]() $\{ P_{\boldsymbol {i}}(\mathbf {a}) \mid \mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K} \}$ the PBW basis of
$\{ P_{\boldsymbol {i}}(\mathbf {a}) \mid \mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K} \}$ the PBW basis of ![]() $\mathscr {C}_w$ associated with
$\mathscr {C}_w$ associated with ![]() ${\boldsymbol {i}}$.
${\boldsymbol {i}}$.
For a simple module ![]() $X$ such that
$X$ such that ![]() $X\simeq {\operatorname {hd}}(P_{\boldsymbol {i}}(\mathbf {a}))$, we set
$X\simeq {\operatorname {hd}}(P_{\boldsymbol {i}}(\mathbf {a}))$, we set
The following lemma says that the operation ![]() ${\rm PBW}_{\boldsymbol {i}}( - \triangledown \mathcal {M}^{\boldsymbol {i}}(\mathbf {a}))$ on the set of simple modules behaves very nicely, where
${\rm PBW}_{\boldsymbol {i}}( - \triangledown \mathcal {M}^{\boldsymbol {i}}(\mathbf {a}))$ on the set of simple modules behaves very nicely, where ![]() $\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})$ is defined in (2.5).
$\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})$ is defined in (2.5).
Lemma 4.1 (cf. [Reference Kashiwara and KimKK19, Lemma 3.11 and Proposition 3.14])
For ![]() $M=\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})$ with
$M=\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})$ with ![]() $\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^{\mathsf {K}}$ and a simple module
$\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^{\mathsf {K}}$ and a simple module ![]() $X$, we have
$X$, we have
In particular, ![]() $\mathbf {c}\mathbin {:=}{\rm PBW}_{\boldsymbol {i}}\big (\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})\big )$ is given by
$\mathbf {c}\mathbin {:=}{\rm PBW}_{\boldsymbol {i}}\big (\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})\big )$ is given by ![]() $\mathbf {c}_k=\sum _{j}\mathbf {a}_j$ where
$\mathbf {c}_k=\sum _{j}\mathbf {a}_j$ where ![]() $j$ ranges over
$j$ ranges over ![]() $j\in [1,r]$ such that
$j\in [1,r]$ such that ![]() $j\geqslant k$ and
$j\geqslant k$ and ![]() ${\boldsymbol {i}}_j={\boldsymbol {i}}_k$.
${\boldsymbol {i}}_j={\boldsymbol {i}}_k$.
Proof. It is enough to show it when ![]() $M=M^{\boldsymbol {i}}_k$. Note that
$M=M^{\boldsymbol {i}}_k$. Note that
where ![]() $\mathbf {n}=(\mathbf {n}_1,\ldots,\mathbf {n}_r) = {\rm PBW}_{\boldsymbol {i}}(X)$,
$\mathbf {n}=(\mathbf {n}_1,\ldots,\mathbf {n}_r) = {\rm PBW}_{\boldsymbol {i}}(X)$, ![]() $Y \simeq {\operatorname {hd}}\Big (\displaystyle \circ _{1 \leqslant k \leqslant r-1}^{\to } {S^{\boldsymbol {i}}_k}^{\circ \mathbf {n}_k } \Big )$ and
$Y \simeq {\operatorname {hd}}\Big (\displaystyle \circ _{1 \leqslant k \leqslant r-1}^{\to } {S^{\boldsymbol {i}}_k}^{\circ \mathbf {n}_k } \Big )$ and ![]() $\displaystyle \circ _{p \leqslant k \leqslant q}^{\to } X_k$ denotes the ordered convolution product
$\displaystyle \circ _{p \leqslant k \leqslant q}^{\to } X_k$ denotes the ordered convolution product ![]() $X_q \circ X_{q-1} \circ \cdots X_{p+1} \circ X_p$ for
$X_q \circ X_{q-1} \circ \cdots X_{p+1} \circ X_p$ for ![]() $X_k$ in
$X_k$ in ![]() $R\text {-}\mathrm {gmod}$.
$R\text {-}\mathrm {gmod}$.
If ![]() $r > k$, then
$r > k$, then ![]() $({S^{\boldsymbol {i}}_r}^{\circ \mathbf {n}_r},M^{\boldsymbol {i}}_k)$ is unmixed and, hence,
$({S^{\boldsymbol {i}}_r}^{\circ \mathbf {n}_r},M^{\boldsymbol {i}}_k)$ is unmixed and, hence, ![]() ${S^{\boldsymbol {i}}_r}^{\circ \mathbf {n}_r} \circ Y \circ M^{\boldsymbol {i}}_k$ has a simple head. We have
${S^{\boldsymbol {i}}_r}^{\circ \mathbf {n}_r} \circ Y \circ M^{\boldsymbol {i}}_k$ has a simple head. We have
 \begin{align*} X \triangledown M^{\boldsymbol{i}}_k & \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \circ Y \circ M^{\boldsymbol{i}}_k) \\ & \simeq {S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \triangledown (Y \triangledown M^{\boldsymbol{i}}_k) \simeq {S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \triangledown {\operatorname{hd}}\bigg( \displaystyle\circ_{1 \leqslant k \leqslant r-1}^{\to} {S^{\boldsymbol{i}}_k}^{\circ \mathbf{c}_k} \bigg), \end{align*}
\begin{align*} X \triangledown M^{\boldsymbol{i}}_k & \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \circ Y \circ M^{\boldsymbol{i}}_k) \\ & \simeq {S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \triangledown (Y \triangledown M^{\boldsymbol{i}}_k) \simeq {S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \triangledown {\operatorname{hd}}\bigg( \displaystyle\circ_{1 \leqslant k \leqslant r-1}^{\to} {S^{\boldsymbol{i}}_k}^{\circ \mathbf{c}_k} \bigg), \end{align*}
where ![]() $\mathbf {c} ={\rm PBW}_{\boldsymbol {i}}(Y)+{\rm PBW}_{\boldsymbol {i}}(M^{\boldsymbol {i}}_k)$ by induction on
$\mathbf {c} ={\rm PBW}_{\boldsymbol {i}}(Y)+{\rm PBW}_{\boldsymbol {i}}(M^{\boldsymbol {i}}_k)$ by induction on ![]() $r$. Thus, our assertion follows in this case.
$r$. Thus, our assertion follows in this case.
If ![]() $r = k$, then
$r = k$, then ![]() $M^{\boldsymbol {i}}_r$ commutes with all the objects of
$M^{\boldsymbol {i}}_r$ commutes with all the objects of ![]() $\mathscr {C}_w$ and, hence, we have
$\mathscr {C}_w$ and, hence, we have
 \begin{align*} X \triangledown M^{\boldsymbol{i}}_r & \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \circ M^{\boldsymbol{i}}_r \circ {S^{\boldsymbol{i}}_{r-1}}^{\circ \mathbf{n}_{r-1}} \circ \cdots {S^{\boldsymbol{i}}_{1}}^{\circ \mathbf{n}_{1}} ) \\ & \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \circ M^{\boldsymbol{i}}_r) \triangledown Y \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \circ (S^{\boldsymbol{i}}_r \triangledown M^{\boldsymbol{i}}_{r_-})) \triangledown Y \\ & \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r+1} \triangledown M^{\boldsymbol{i}}_{r_-} ) \triangledown Y \simeq {S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r+1} \triangledown (M^{\boldsymbol{i}}_{r_-} \circ Y ), \end{align*}
\begin{align*} X \triangledown M^{\boldsymbol{i}}_r & \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \circ M^{\boldsymbol{i}}_r \circ {S^{\boldsymbol{i}}_{r-1}}^{\circ \mathbf{n}_{r-1}} \circ \cdots {S^{\boldsymbol{i}}_{1}}^{\circ \mathbf{n}_{1}} ) \\ & \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \circ M^{\boldsymbol{i}}_r) \triangledown Y \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r} \circ (S^{\boldsymbol{i}}_r \triangledown M^{\boldsymbol{i}}_{r_-})) \triangledown Y \\ & \simeq {\operatorname{hd}}({S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r+1} \triangledown M^{\boldsymbol{i}}_{r_-} ) \triangledown Y \simeq {S^{\boldsymbol{i}}_r}^{\circ \mathbf{n}_r+1} \triangledown (M^{\boldsymbol{i}}_{r_-} \circ Y ), \end{align*}
where the last isomorphism follows from the commutativity of ![]() $M^{\boldsymbol {i}}_{r_-}$ and
$M^{\boldsymbol {i}}_{r_-}$ and ![]() $Y$. Then our assertion follows from the induction hypothesis.
$Y$. Then our assertion follows from the induction hypothesis.
The lemma above gives a direct proof of the following corollary although it follows immediately from Proposition 3.6.
Corollary 4.2 For any reduced sequence ![]() ${\boldsymbol {i}}$ for
${\boldsymbol {i}}$ for ![]() $w$, the commuting family
$w$, the commuting family ![]() $\mathcal {M}^{\boldsymbol {i}}$ is independent.
$\mathcal {M}^{\boldsymbol {i}}$ is independent.
The following proposition is proved in [Reference Kashiwara and KimKK19, Proposition 2.11] for symmetric quiver Hecke algebra and the same proof also works for the general case.
Proposition 4.3 For any ![]() $\mathbf {a} = (\mathbf {a}_1,\ldots,\mathbf {a}_r)$,
$\mathbf {a} = (\mathbf {a}_1,\ldots,\mathbf {a}_r)$, ![]() $\mathbf {b} = (\mathbf {b}_1,\ldots,\mathbf {b}_r) \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$, the ordered sequence
$\mathbf {b} = (\mathbf {b}_1,\ldots,\mathbf {b}_r) \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$, the ordered sequence
is a normal sequence.
The statement and proof of following proposition are the same as [Reference Kashiwara and KimKK19, Proposition 3.14] even though [Reference Kashiwara and KimKK19] dealt only with symmetric quiver Hecke algebras. Here we repeat it in order to show relations between explicit ![]() $\mathbb {Z}\mspace {1mu}_{\geqslant 0}$-vectors associated with a simple module
$\mathbb {Z}\mspace {1mu}_{\geqslant 0}$-vectors associated with a simple module ![]() $X$ in
$X$ in ![]() $\mathscr {C}_w$ for the readers’ convenience.
$\mathscr {C}_w$ for the readers’ convenience.
Proposition 4.4 For a simple module ![]() $X$ in
$X$ in ![]() $\mathscr {C}_w$ or
$\mathscr {C}_w$ or ![]() $\widetilde {\mathscr {C}}_w$, there exist
$\widetilde {\mathscr {C}}_w$, there exist ![]() $\mathbf {a}, \mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$ such that
$\mathbf {a}, \mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^\mathsf {K}$ such that
Proof. In this proof, we sometimes drop ![]() $^{\boldsymbol {i}}$ for notational simplicity. It is enough to consider when
$^{\boldsymbol {i}}$ for notational simplicity. It is enough to consider when ![]() $X \in \mathscr {C}_w$ by part (D) in (2.6). Note that there exists a unique
$X \in \mathscr {C}_w$ by part (D) in (2.6). Note that there exists a unique ![]() $\mathbf {c} = (\mathbf {c}_1,\ldots,\mathbf {c}_r) \in \mathbb {Z}\mspace {1mu}^\mathsf {K}_{\geqslant 0}$ such that
$\mathbf {c} = (\mathbf {c}_1,\ldots,\mathbf {c}_r) \in \mathbb {Z}\mspace {1mu}^\mathsf {K}_{\geqslant 0}$ such that
Set ![]() $\mathbf {c}_+ \mathbin {:=} \sum _{k=1}^r \mathbf {c}_{k_+} \mathbf {e}_k= \sum _{j \in \mathsf {K}} \mathbf {c}_k \mathbf {e}_{k_-}$, where
$\mathbf {c}_+ \mathbin {:=} \sum _{k=1}^r \mathbf {c}_{k_+} \mathbf {e}_k= \sum _{j \in \mathsf {K}} \mathbf {c}_k \mathbf {e}_{k_-}$, where ![]() $\{ \mathbf {e}_j \mid j \in \mathsf {K}\}$ is the standard basis of
$\{ \mathbf {e}_j \mid j \in \mathsf {K}\}$ is the standard basis of ![]() $\mathbb {Z}\mspace {1mu}^\mathsf {K}$ such that
$\mathbb {Z}\mspace {1mu}^\mathsf {K}$ such that ![]() $\mathbf {c} = \sum _{j \in \mathsf {K}} \mathbf {c}_j \mathbf {e}_j$. Then we have
$\mathbf {c} = \sum _{j \in \mathsf {K}} \mathbf {c}_j \mathbf {e}_j$. Then we have ![]() $\mathcal {M}^{\boldsymbol {i}}(\mathbf {c}_+) \simeq M_{1_-}^{\circ \mathbf {c}_1} \circ \cdots \circ M_{r_-}^{\circ \mathbf {c}_r}$. By (4.1) and Proposition 4.3, we have
$\mathcal {M}^{\boldsymbol {i}}(\mathbf {c}_+) \simeq M_{1_-}^{\circ \mathbf {c}_1} \circ \cdots \circ M_{r_-}^{\circ \mathbf {c}_r}$. By (4.1) and Proposition 4.3, we have
 \begin{align*} X \triangledown \mathcal{M}^{\boldsymbol{i}}(\mathbf{c}_+) &\simeq {\operatorname{hd}}(S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_1^{\circ \mathbf{c}_{1}} \circ \mathcal{M}^{\boldsymbol{i}}(\mathbf{c}_+) ) \\ &\simeq {\operatorname{hd}}(S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_2^{\circ \mathbf{c}_{2}} \circ S_1^{\circ \mathbf{c}_{1}} \circ M_{1_-}^{\circ \mathbf{c}_1} \circ M_{2_-}^{\circ \mathbf{c}_2} \circ \cdots \circ M_{r_-}^{\circ \mathbf{c}_r} ) \\ &\simeq {\operatorname{hd}}((S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_2^{\circ \mathbf{c}_{2}}) \circ (S_1^{\circ \mathbf{c}_{1}} \triangledown M_{1_-}^{\circ \mathbf{c}_1}) \circ (M_{2_-}^{\circ \mathbf{c}_2} \circ \cdots \circ M_{r_-}^{\circ \mathbf{c}_r} )) \\ &\simeq {\operatorname{hd}}((S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_1^{\circ \mathbf{c}_{2}}) \circ M_{1}^{\circ \mathbf{c}_1} \circ (M_{2_-}^{\circ \mathbf{c}_2} \circ \cdots \circ M_{r_-}^{\circ \mathbf{c}_r} )) \\ &\simeq {\operatorname{hd}}((S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_2^{\circ \mathbf{c}_{2}}) \circ (M_{2_-}^{\circ \mathbf{c}_2} \circ \cdots \circ M_{r_-}^{\circ \mathbf{c}_r} )\circ M_{1}^{\circ \mathbf{c}_1} ) \\ &\simeq \cdots \simeq {\operatorname{hd}}(M_r^{\circ \mathbf{c}_r} \circ \cdots \circ M_1^{\circ \mathbf{c}_1}) \simeq \mathcal{M}^{\boldsymbol{i}}(\mathbf{c}), \end{align*}
\begin{align*} X \triangledown \mathcal{M}^{\boldsymbol{i}}(\mathbf{c}_+) &\simeq {\operatorname{hd}}(S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_1^{\circ \mathbf{c}_{1}} \circ \mathcal{M}^{\boldsymbol{i}}(\mathbf{c}_+) ) \\ &\simeq {\operatorname{hd}}(S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_2^{\circ \mathbf{c}_{2}} \circ S_1^{\circ \mathbf{c}_{1}} \circ M_{1_-}^{\circ \mathbf{c}_1} \circ M_{2_-}^{\circ \mathbf{c}_2} \circ \cdots \circ M_{r_-}^{\circ \mathbf{c}_r} ) \\ &\simeq {\operatorname{hd}}((S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_2^{\circ \mathbf{c}_{2}}) \circ (S_1^{\circ \mathbf{c}_{1}} \triangledown M_{1_-}^{\circ \mathbf{c}_1}) \circ (M_{2_-}^{\circ \mathbf{c}_2} \circ \cdots \circ M_{r_-}^{\circ \mathbf{c}_r} )) \\ &\simeq {\operatorname{hd}}((S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_1^{\circ \mathbf{c}_{2}}) \circ M_{1}^{\circ \mathbf{c}_1} \circ (M_{2_-}^{\circ \mathbf{c}_2} \circ \cdots \circ M_{r_-}^{\circ \mathbf{c}_r} )) \\ &\simeq {\operatorname{hd}}((S_r^{\circ \mathbf{c}_r} \circ S_{r-1}^{\circ \mathbf{c}_{r-1}} \circ \cdots \circ S_2^{\circ \mathbf{c}_{2}}) \circ (M_{2_-}^{\circ \mathbf{c}_2} \circ \cdots \circ M_{r_-}^{\circ \mathbf{c}_r} )\circ M_{1}^{\circ \mathbf{c}_1} ) \\ &\simeq \cdots \simeq {\operatorname{hd}}(M_r^{\circ \mathbf{c}_r} \circ \cdots \circ M_1^{\circ \mathbf{c}_1}) \simeq \mathcal{M}^{\boldsymbol{i}}(\mathbf{c}), \end{align*}
which implies our assertion.
As seen by the proof of the above proposition and Proposition 3.6, we have the following.
Proposition 4.5 The commuting family ![]() $\mathcal {M}^{\boldsymbol {i}}$ is a Laurent family. Moreover, for a simple module
$\mathcal {M}^{\boldsymbol {i}}$ is a Laurent family. Moreover, for a simple module ![]() $M$, two vectors
$M$, two vectors ![]() $\mathbf {a}={\rm PBW}_{\boldsymbol {i}}(M)$ and
$\mathbf {a}={\rm PBW}_{\boldsymbol {i}}(M)$ and ![]() $\mathbf {g}\mathbin {:=}\mathbf {g}_{\boldsymbol {i}}^R(M)$ are related by
$\mathbf {g}\mathbin {:=}\mathbf {g}_{\boldsymbol {i}}^R(M)$ are related by
where ![]() $\mathbf {a}_{r+1}=0$.
$\mathbf {a}_{r+1}=0$.
The following corollary can be proved by the same arguments in [Reference Kashiwara and KimKK19].
Corollary 4.6 Let ![]() ${\boldsymbol {i}}$ be a reduced sequence of
${\boldsymbol {i}}$ be a reduced sequence of ![]() $w$.
$w$.
(i) For a dual pair of simples
 $(L,R)$ in
$(L,R)$ in  $\widetilde {\mathscr {C}}_w$, we have
$\widetilde {\mathscr {C}}_w$, we have
 \[ \mathbf{g}_{\boldsymbol{i}}^R(L)+ \mathbf{g}_{\boldsymbol{i}}^L (R)=0. \]
\[ \mathbf{g}_{\boldsymbol{i}}^R(L)+ \mathbf{g}_{\boldsymbol{i}}^L (R)=0. \]
(ii) The maps
 $\mathbf {g}_{\boldsymbol {i}}^R, \mathbf {g}_{\boldsymbol {i}}^L \colon {\rm Irr}(\widetilde {\mathscr {C}}_w) \to \mathbb {Z}\mspace {1mu}^\mathsf {K}$ are bijective.
$\mathbf {g}_{\boldsymbol {i}}^R, \mathbf {g}_{\boldsymbol {i}}^L \colon {\rm Irr}(\widetilde {\mathscr {C}}_w) \to \mathbb {Z}\mspace {1mu}^\mathsf {K}$ are bijective.
5. Skew-symmetric pairings
In this section, we study skew-symmetric pairings induced by the ![]() $\mathbb {Z}\mspace {1mu}$-vectors associated with simple modules.
$\mathbb {Z}\mspace {1mu}$-vectors associated with simple modules.
5.1 Skew-symmetric pairing associated with a quasi-Laurent family
Let ![]() $\mathscr {C}$ be a full monoidal subcategory of
$\mathscr {C}$ be a full monoidal subcategory of ![]() $R\text {-}\mathrm {gmod}$ stable by taking subquotients, extensions and grading shifts, and let
$R\text {-}\mathrm {gmod}$ stable by taking subquotients, extensions and grading shifts, and let ![]() $\mathcal {M}=\{ M_j \mid j \in J\}$ be a quasi-Laurent family in
$\mathcal {M}=\{ M_j \mid j \in J\}$ be a quasi-Laurent family in ![]() $\mathscr {C}$ labeled by a finite index set
$\mathscr {C}$ labeled by a finite index set ![]() $J$.
$J$.
For ![]() $X,Y \in {\rm Irr}(\mathscr {C})$, let us define
$X,Y \in {\rm Irr}(\mathscr {C})$, let us define
 \begin{align}
{\mathrm G}^R_\mathcal{M}(X,Y) &\mathbin{:=} \sum\limits_{
a,b \in J} (\mathbf{g}^R_\mathcal{M}(X))_a
(\mathbf{g}^R_\mathcal{M}(Y))_b \, \Lambda(M_a,M_b) \quad \text{and}\nonumber\\
{\mathrm G}^L_\mathcal{M}(X,Y) &\mathbin{:=}
\sum\limits_{ a,b \in J} (\mathbf{g}^L_\mathcal{M}(X))_a
(\mathbf{g}^L_\mathcal{M}(Y))_b \, \Lambda(M_a,M_b).
\end{align}
\begin{align}
{\mathrm G}^R_\mathcal{M}(X,Y) &\mathbin{:=} \sum\limits_{
a,b \in J} (\mathbf{g}^R_\mathcal{M}(X))_a
(\mathbf{g}^R_\mathcal{M}(Y))_b \, \Lambda(M_a,M_b) \quad \text{and}\nonumber\\
{\mathrm G}^L_\mathcal{M}(X,Y) &\mathbin{:=}
\sum\limits_{ a,b \in J} (\mathbf{g}^L_\mathcal{M}(X))_a
(\mathbf{g}^L_\mathcal{M}(Y))_b \, \Lambda(M_a,M_b).
\end{align}
The following lemma immediately follows from Lemma 3.9.
Lemma 5.1 For ![]() $M=\mathcal {M}(\mathbf {a})$ with
$M=\mathcal {M}(\mathbf {a})$ with ![]() $\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ and
$\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ and ![]() $X,Y \in {\rm Irr}(\mathscr {C})$, we have
$X,Y \in {\rm Irr}(\mathscr {C})$, we have
 \begin{align*} &{\mathrm G}^R_\mathcal{M}(X \triangledown M,Y) = {\mathrm G}^R_\mathcal{M}(X,Y)+ {\mathrm G}^R_\mathcal{M}(M,Y), \quad {\mathrm G}^R_\mathcal{M}(X,Y) = -{\mathrm G}^R_\mathcal{M}(Y,X), \\ &{\mathrm G}^L_\mathcal{M}(X \triangle M,Y) = {\mathrm G}^L_\mathcal{M}(X,Y)+ {\mathrm G}^L_\mathcal{M}(M,Y), \quad {\mathrm G}^L_\mathcal{M}(X,Y) = -{\mathrm G}^L_\mathcal{M}(Y,X). \end{align*}
\begin{align*} &{\mathrm G}^R_\mathcal{M}(X \triangledown M,Y) = {\mathrm G}^R_\mathcal{M}(X,Y)+ {\mathrm G}^R_\mathcal{M}(M,Y), \quad {\mathrm G}^R_\mathcal{M}(X,Y) = -{\mathrm G}^R_\mathcal{M}(Y,X), \\ &{\mathrm G}^L_\mathcal{M}(X \triangle M,Y) = {\mathrm G}^L_\mathcal{M}(X,Y)+ {\mathrm G}^L_\mathcal{M}(M,Y), \quad {\mathrm G}^L_\mathcal{M}(X,Y) = -{\mathrm G}^L_\mathcal{M}(Y,X). \end{align*}
Proposition 5.2 Let ![]() $X$ be a simple module in
$X$ be a simple module in ![]() $\mathscr {C}$. Then for any
$\mathscr {C}$. Then for any ![]() $\mathbf {c}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^J$, we have
$\mathbf {c}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^J$, we have
Proof. If ![]() $X$ is also of the form
$X$ is also of the form ![]() $\mathcal {M}(\mathbf {d})$, it is obvious. Set
$\mathcal {M}(\mathbf {d})$, it is obvious. Set ![]() $Y=\mathcal {M}(\mathbf {c})$.
$Y=\mathcal {M}(\mathbf {c})$.
(i) Note that there exist
 $\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ such that
$\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ such that  $X \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$. Then we have
Since
$X \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$. Then we have
Since \begin{align*} \Lambda(X,Y)+\Lambda(\mathcal{M}(\mathbf{a}),Y) = \Lambda(X\triangledown \mathcal{M}(\mathbf{a}),Y) & = {\mathrm G}^R_\mathcal{M}(X\triangledown \mathcal{M}(\mathbf{a}),Y) \\ & = {\mathrm G}^R_\mathcal{M}(X,Y) + {\mathrm G}^R_\mathcal{M}(\mathcal{M}(\mathbf{a}),Y). \end{align*}
\begin{align*} \Lambda(X,Y)+\Lambda(\mathcal{M}(\mathbf{a}),Y) = \Lambda(X\triangledown \mathcal{M}(\mathbf{a}),Y) & = {\mathrm G}^R_\mathcal{M}(X\triangledown \mathcal{M}(\mathbf{a}),Y) \\ & = {\mathrm G}^R_\mathcal{M}(X,Y) + {\mathrm G}^R_\mathcal{M}(\mathcal{M}(\mathbf{a}),Y). \end{align*}
 $\Lambda (\mathcal {M}(\mathbf {a}),Y) = {\mathrm G}^R_\mathcal {M}(\mathcal {M}(\mathbf {a}),Y)$, our assertion follows.
$\Lambda (\mathcal {M}(\mathbf {a}),Y) = {\mathrm G}^R_\mathcal {M}(\mathcal {M}(\mathbf {a}),Y)$, our assertion follows.(ii) Similarly, there exist
 $\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ such that
$\mathbf {a},\mathbf {b} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ such that  $\mathcal {M}(\mathbf {a}) \triangledown X \simeq \mathcal {M}(\mathbf {b})$. Then we have
Then our assertion follows from the fact that
$\mathcal {M}(\mathbf {a}) \triangledown X \simeq \mathcal {M}(\mathbf {b})$. Then we have
Then our assertion follows from the fact that \begin{align*} \Lambda(Y,\mathcal{M}(\mathbf{a})) + \Lambda(Y,X) = \Lambda(Y,\mathcal{M}(\mathbf{a})\triangledown X) & = {\mathrm G}^L_\mathcal{M}(Y,\mathcal{M}(\mathbf{a})\triangledown X) \\ & = {\mathrm G}^L_\mathcal{M}(Y,\mathcal{M}(\mathbf{a})) + {\mathrm G}^L_\mathcal{M}(Y,X). \end{align*}
\begin{align*} \Lambda(Y,\mathcal{M}(\mathbf{a})) + \Lambda(Y,X) = \Lambda(Y,\mathcal{M}(\mathbf{a})\triangledown X) & = {\mathrm G}^L_\mathcal{M}(Y,\mathcal{M}(\mathbf{a})\triangledown X) \\ & = {\mathrm G}^L_\mathcal{M}(Y,\mathcal{M}(\mathbf{a})) + {\mathrm G}^L_\mathcal{M}(Y,X). \end{align*}
 $\Lambda (Y,\mathcal {M}(\mathbf {a})) = {\mathrm G}^L_\mathcal {M}(Y,\mathcal {M}(\mathbf {a}))$.
$\Lambda (Y,\mathcal {M}(\mathbf {a})) = {\mathrm G}^L_\mathcal {M}(Y,\mathcal {M}(\mathbf {a}))$.
Proposition 5.3 For any simple modules ![]() $X,Y$ in
$X,Y$ in ![]() $\mathscr {C}$ such that one of them is affreal, we have
$\mathscr {C}$ such that one of them is affreal, we have
Proof. Since the proofs are similar, we will consider the case of ![]() ${\mathrm G}^R_\mathcal {M}$. Take
${\mathrm G}^R_\mathcal {M}$. Take ![]() $\mathbf {a},\mathbf {b}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^J$ such that
$\mathbf {a},\mathbf {b}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^J$ such that ![]() $Y \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$. Then we have
$Y \triangledown \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b})$. Then we have
 \begin{align*} {\mathrm G}^R_\mathcal{M}(X,Y) + {\mathrm G}^R_\mathcal{M}(X,\mathcal{M}(\mathbf{a}))& = {\mathrm G}^R_\mathcal{M}(X,Y\triangledown\mathcal{M}(\mathbf{a})) \\ & = \Lambda(X,Y \triangledown \mathcal{M}(\mathbf{a})) \leqslant \Lambda(X,Y)+ \Lambda(X,\mathcal{M}(\mathbf{a})) \\ & = \Lambda(X,Y)+ {\mathrm G}^R_\mathcal{M}(X,\mathcal{M}(\mathbf{a})) , \end{align*}
\begin{align*} {\mathrm G}^R_\mathcal{M}(X,Y) + {\mathrm G}^R_\mathcal{M}(X,\mathcal{M}(\mathbf{a}))& = {\mathrm G}^R_\mathcal{M}(X,Y\triangledown\mathcal{M}(\mathbf{a})) \\ & = \Lambda(X,Y \triangledown \mathcal{M}(\mathbf{a})) \leqslant \Lambda(X,Y)+ \Lambda(X,\mathcal{M}(\mathbf{a})) \\ & = \Lambda(X,Y)+ {\mathrm G}^R_\mathcal{M}(X,\mathcal{M}(\mathbf{a})) , \end{align*}
which yields our assertion. Here, the inequality follows from [Reference Kang, Kashiwara, Kim and OhKKKO18, Proposition 3.2.10].
Proposition 5.4 If simple modules ![]() $X$ and
$X$ and ![]() $Y$ in
$Y$ in ![]() $\mathscr {C}$ commute and one of them is affreal, then we have
$\mathscr {C}$ commute and one of them is affreal, then we have
Proof. Since the proofs are similar, we will only give the proof for ![]() ${\mathrm G}^R_\mathcal {M}$. By the preceding proposition, we have
${\mathrm G}^R_\mathcal {M}$. By the preceding proposition, we have
 \begin{align*} 0&=\big(\Lambda(X,Y)+\Lambda(Y,X)\big)-\big({\mathrm G}^R_\mathcal{M}(X,Y)+{\mathrm G}^R_\mathcal{M}(Y,X)\big)\\ &=\big(\Lambda(X,Y)-{\mathrm G}^R_\mathcal{M}(X,Y)\big)+\big( \Lambda(Y,X)-{\mathrm G}^R_\mathcal{M}(Y,X)\big) \ge0, \end{align*}
\begin{align*} 0&=\big(\Lambda(X,Y)+\Lambda(Y,X)\big)-\big({\mathrm G}^R_\mathcal{M}(X,Y)+{\mathrm G}^R_\mathcal{M}(Y,X)\big)\\ &=\big(\Lambda(X,Y)-{\mathrm G}^R_\mathcal{M}(X,Y)\big)+\big( \Lambda(Y,X)-{\mathrm G}^R_\mathcal{M}(Y,X)\big) \ge0, \end{align*}
which implies ![]() $\Lambda (X,Y)-{\mathrm G}^R_\mathcal {M}(X,Y)=0$.
$\Lambda (X,Y)-{\mathrm G}^R_\mathcal {M}(X,Y)=0$.
Remark 5.5 The two invariants ![]() ${{\mathrm G}}^R_{{\mathcal {M}}}(X,Y)$ and
${{\mathrm G}}^R_{{\mathcal {M}}}(X,Y)$ and ![]() ${{\mathrm G}}^L_{{\mathcal {M}}}(X,Y)$ are different in general and depend on the choice of
${{\mathrm G}}^L_{{\mathcal {M}}}(X,Y)$ are different in general and depend on the choice of ![]() $\mathcal {M}$.
$\mathcal {M}$.
Let ![]() $w_0$ be the longest element of finite type
$w_0$ be the longest element of finite type ![]() $A_2$. For a reduced sequence
$A_2$. For a reduced sequence ![]() ${\boldsymbol {i}}=(1,2,1)$ of
${\boldsymbol {i}}=(1,2,1)$ of ![]() $w_0$, we have
$w_0$, we have
while
for the other reduced sequence ![]() ${\boldsymbol {j}}=(2,1,2)$ of
${\boldsymbol {j}}=(2,1,2)$ of ![]() $w_0$. Here
$w_0$. Here ![]() $\langle k\rangle$
$\langle k\rangle$ ![]() $(k=1,2)$ is a one-dimensional
$(k=1,2)$ is a one-dimensional ![]() $R({\mspace {1mu}\alpha }_k)$-module, and
$R({\mspace {1mu}\alpha }_k)$-module, and ![]() $\langle 12 \rangle$ and
$\langle 12 \rangle$ and ![]() $\langle 21 \rangle$ are one-dimensional
$\langle 21 \rangle$ are one-dimensional ![]() $R({\mspace {1mu}\alpha }_1+{\mspace {1mu}\alpha }_2)$-modules (see [Reference Kang, Kashiwara and KimKKK18] for more details on these modules).
$R({\mspace {1mu}\alpha }_1+{\mspace {1mu}\alpha }_2)$-modules (see [Reference Kang, Kashiwara and KimKKK18] for more details on these modules).
Since ![]() $A_2$ is symmetric,
$A_2$ is symmetric, ![]() $\mathcal {M}' \mathbin {:=} \mu _1(\mathcal {M}^{\boldsymbol {i}})$ is also a Laurent family given as follows:
$\mathcal {M}' \mathbin {:=} \mu _1(\mathcal {M}^{\boldsymbol {i}})$ is also a Laurent family given as follows:
Note that ![]() $\mathcal {M}'=\mathcal {M}^{\boldsymbol {j}}$ (up to an index permutation). We have
$\mathcal {M}'=\mathcal {M}^{\boldsymbol {j}}$ (up to an index permutation). We have
 \begin{align*} & \mathbf{g}^R_{\mathcal{M}^{\boldsymbol{i}}}(\langle 1 \rangle) = \mathbf{g}^L_{\mathcal{M}^{\boldsymbol{i}}}(\langle 1 \rangle) = (1,0,0), \quad \mathbf{g}^R_{\mathcal{M}^{\boldsymbol{i}}}(\langle 2 \rangle ) = (-1,0,1), \quad \mathbf{g}^L_{\mathcal{M}^{\boldsymbol{i}}}(\langle 2 \rangle ) = (-1,1,0), \\ & \mathbf{g}^R_{\mathcal{M}'}(\langle 1 \rangle) = (-1,1,0), \quad \mathbf{g}^L_{\mathcal{M}'}(\langle 1 \rangle) = (-1,0,1), \quad \mathbf{g}^R_{\mathcal{M}'}(\langle 2 \rangle) = \mathbf{g}^L_{\mathcal{M}'}(\langle 2 \rangle) = (1,0,0), \end{align*}
\begin{align*} & \mathbf{g}^R_{\mathcal{M}^{\boldsymbol{i}}}(\langle 1 \rangle) = \mathbf{g}^L_{\mathcal{M}^{\boldsymbol{i}}}(\langle 1 \rangle) = (1,0,0), \quad \mathbf{g}^R_{\mathcal{M}^{\boldsymbol{i}}}(\langle 2 \rangle ) = (-1,0,1), \quad \mathbf{g}^L_{\mathcal{M}^{\boldsymbol{i}}}(\langle 2 \rangle ) = (-1,1,0), \\ & \mathbf{g}^R_{\mathcal{M}'}(\langle 1 \rangle) = (-1,1,0), \quad \mathbf{g}^L_{\mathcal{M}'}(\langle 1 \rangle) = (-1,0,1), \quad \mathbf{g}^R_{\mathcal{M}'}(\langle 2 \rangle) = \mathbf{g}^L_{\mathcal{M}'}(\langle 2 \rangle) = (1,0,0), \end{align*}
and
Note that ![]() $\Lambda (X,X)=0$ for an affreal simple module
$\Lambda (X,X)=0$ for an affreal simple module ![]() $X$. Thus, we have
$X$. Thus, we have
Thus, for a non-commuting pair of simple modules ![]() $(X,Y)$ in
$(X,Y)$ in ![]() $\mathscr {C}$, the
$\mathscr {C}$, the ![]() $\mathbb {Z}\mspace {1mu}$-values
$\mathbb {Z}\mspace {1mu}$-values ![]() ${\mathrm G}^R_\mathcal {M}(X,Y)$ and
${\mathrm G}^R_\mathcal {M}(X,Y)$ and ![]() ${\mathrm G}^L_\mathcal {M}(X,Y)$ do depend on the choice of a quasi-Laurent commuting family
${\mathrm G}^L_\mathcal {M}(X,Y)$ do depend on the choice of a quasi-Laurent commuting family ![]() $\mathcal {M}$.
$\mathcal {M}$.
5.2 Skew-symmetric pairing associated with the GLS cluster
Let ![]() $w \in \mathsf {W}$ and
$w \in \mathsf {W}$ and ![]() ${\boldsymbol {i}}=(i_1,\ldots,i_r)$ a reduced sequence of
${\boldsymbol {i}}=(i_1,\ldots,i_r)$ a reduced sequence of ![]() $w$. Let
$w$. Let ![]() $\mathcal {M}^{\boldsymbol {i}}$ be the associated GLS cluster. For such a Laurent family, we can define
$\mathcal {M}^{\boldsymbol {i}}$ be the associated GLS cluster. For such a Laurent family, we can define ![]() ${\mathrm G}_{\mathcal {M}^{\boldsymbol {i}}}^R$ in terms of PBW decompositions.
${\mathrm G}_{\mathcal {M}^{\boldsymbol {i}}}^R$ in terms of PBW decompositions.
We define a skew-symmetric ![]() $\mathbb {Z}\mspace {1mu}$-valued map
$\mathbb {Z}\mspace {1mu}$-valued map ![]() $\lambda ^{\boldsymbol {i}}\colon [1,r]\times [1,r]\to \mathbb {Z}\mspace {1mu}$ by
$\lambda ^{\boldsymbol {i}}\colon [1,r]\times [1,r]\to \mathbb {Z}\mspace {1mu}$ by
for ![]() $1 \leqslant a,b\leqslant r$.
$1 \leqslant a,b\leqslant r$.
Remark 5.6 The skew-symmetric map ![]() $\lambda ^{\boldsymbol {i}}$ in (5.4) is known when
$\lambda ^{\boldsymbol {i}}$ in (5.4) is known when ![]() $\mathfrak {g}$ is of finite type and
$\mathfrak {g}$ is of finite type and ![]() ${\boldsymbol {i}}$ is adapted to a
${\boldsymbol {i}}$ is adapted to a ![]() $Q$-datum (see [Reference Hernandez and LeclercHL15, Proposition 3.2], [Reference Fujita and OhFO21, Proposition 5.21] and [Reference Kashiwara and OhKaOh23, Theorem 5.4]).
$Q$-datum (see [Reference Hernandez and LeclercHL15, Proposition 3.2], [Reference Fujita and OhFO21, Proposition 5.21] and [Reference Kashiwara and OhKaOh23, Theorem 5.4]).
Let us recall the notion of ![]() ${\boldsymbol {i}}$-box and an affreal simple module
${\boldsymbol {i}}$-box and an affreal simple module ![]() $M^{\boldsymbol {i}}[a,b]$ in
$M^{\boldsymbol {i}}[a,b]$ in ![]() $\mathscr {C}_w$ for an
$\mathscr {C}_w$ for an ![]() ${\boldsymbol {i}}$-box
${\boldsymbol {i}}$-box ![]() $[a,b]$, which are introduced in [Reference Kashiwara, Kim, Oh and ParkKKOP24b].
$[a,b]$, which are introduced in [Reference Kashiwara, Kim, Oh and ParkKKOP24b].
(a) For
 $1 \leqslant a \leqslant b \leqslant r$ such that
$1 \leqslant a \leqslant b \leqslant r$ such that  $i_a=i_b$, we call an interval
$i_a=i_b$, we call an interval  $[a,b]$ an
$[a,b]$ an  ${\boldsymbol {i}}$-box.
${\boldsymbol {i}}$-box.(b) For an
 ${\boldsymbol {i}}$-box
${\boldsymbol {i}}$-box  $[a,b]$, we set
$[a,b]$, we set  $[a,b]_{\boldsymbol {i}} \mathbin {:=} \{ u \mid a \leqslant u \leqslant b, \; i_a=i_u\}$.
$[a,b]_{\boldsymbol {i}} \mathbin {:=} \{ u \mid a \leqslant u \leqslant b, \; i_a=i_u\}$.(c) For an
 ${\boldsymbol {i}}$-box
${\boldsymbol {i}}$-box  $[a,b]$, we set
up to grading shifts. In particular,
$[a,b]$, we set
up to grading shifts. In particular, \begin{align*} M^{\boldsymbol{i}}[a,b] \mathbin{:=} M(w^{\boldsymbol{i}}_{\leqslant b}\varpi_{i_a},w^{\boldsymbol{i}}_{< a}\varpi_{i_a})& \simeq {\operatorname{hd}}\Big( \circ_{u \in [a,b]_{\boldsymbol{i}}}^{\to} S^{\boldsymbol{i}}_u \Big) \\ &\simeq S^{\boldsymbol{i}}_b \triangledown M^{\boldsymbol{i}}[a,b_-] \simeq M^{\boldsymbol{i}}[a_+,b] \triangledown S^{\boldsymbol{i}}_a, \end{align*}
\begin{align*} M^{\boldsymbol{i}}[a,b] \mathbin{:=} M(w^{\boldsymbol{i}}_{\leqslant b}\varpi_{i_a},w^{\boldsymbol{i}}_{< a}\varpi_{i_a})& \simeq {\operatorname{hd}}\Big( \circ_{u \in [a,b]_{\boldsymbol{i}}}^{\to} S^{\boldsymbol{i}}_u \Big) \\ &\simeq S^{\boldsymbol{i}}_b \triangledown M^{\boldsymbol{i}}[a,b_-] \simeq M^{\boldsymbol{i}}[a_+,b] \triangledown S^{\boldsymbol{i}}_a, \end{align*}
 $M^{\boldsymbol {i}}_k = M^{\boldsymbol {i}}[k_{\min },k]$ and
$M^{\boldsymbol {i}}_k = M^{\boldsymbol {i}}[k_{\min },k]$ and  $S^{\boldsymbol {i}}_k = M^{\boldsymbol {i}}[k,k]$.
$S^{\boldsymbol {i}}_k = M^{\boldsymbol {i}}[k,k]$.
Note that ![]() $M^{\boldsymbol {i}}[a,b]$ is an affreal simple module in
$M^{\boldsymbol {i}}[a,b]$ is an affreal simple module in ![]() $\mathscr {C}_w$.
$\mathscr {C}_w$.
Proposition 5.7 For ![]() ${\boldsymbol {i}}$-boxes
${\boldsymbol {i}}$-boxes ![]() $[x,y]$ and
$[x,y]$ and ![]() $[x',y']$ in an interval
$[x',y']$ in an interval ![]() $[1,r]$, assume that
$[1,r]$, assume that
Then we have
Proof. Since the proof is similar, we shall give only the proof of case (a). Let us divide into sub-cases as below.
(i) [![]() $x=y > x'_-$] If
$x=y > x'_-$] If ![]() $x>x'$, we have
$x>x'$, we have
 \begin{align*} \Lambda(S^{\boldsymbol{i}}_x, M^{\boldsymbol{i}}[x',y']) & = \Lambda(S^{\boldsymbol{i}}_x,M^{\boldsymbol{i}}[x'_+,y'] \triangledown S^{\boldsymbol{i}}_{x'}) \\ & \underset{(1)}= \Lambda(S^{\boldsymbol{i}}_x,M^{\boldsymbol{i}}[ x'_+,y'])+ \Lambda(S^{\boldsymbol{i}}_x, S^{\boldsymbol{i}}_{x'})= \Lambda(S^{\boldsymbol{i}}_x,M^{\boldsymbol{i}}[x'_+,y'])+ \lambda^{\boldsymbol{i}}_{x,x'}. \end{align*}
\begin{align*} \Lambda(S^{\boldsymbol{i}}_x, M^{\boldsymbol{i}}[x',y']) & = \Lambda(S^{\boldsymbol{i}}_x,M^{\boldsymbol{i}}[x'_+,y'] \triangledown S^{\boldsymbol{i}}_{x'}) \\ & \underset{(1)}= \Lambda(S^{\boldsymbol{i}}_x,M^{\boldsymbol{i}}[ x'_+,y'])+ \Lambda(S^{\boldsymbol{i}}_x, S^{\boldsymbol{i}}_{x'})= \Lambda(S^{\boldsymbol{i}}_x,M^{\boldsymbol{i}}[x'_+,y'])+ \lambda^{\boldsymbol{i}}_{x,x'}. \end{align*}
Here ![]() $\underset {(1)}=$ holds by [Reference Kashiwara, Kim, Oh and ParkKKOP23, Proposition 2.12] and the fact that
$\underset {(1)}=$ holds by [Reference Kashiwara, Kim, Oh and ParkKKOP23, Proposition 2.12] and the fact that ![]() $(S^{\boldsymbol {i}}_x,S^{\boldsymbol {i}}_{x'})$ is an unmixed pair. Then by the induction hypothesis on
$(S^{\boldsymbol {i}}_x,S^{\boldsymbol {i}}_{x'})$ is an unmixed pair. Then by the induction hypothesis on ![]() $|[x',y']_{\boldsymbol {i}}|$, we have
$|[x',y']_{\boldsymbol {i}}|$, we have
as we desired.
Now, the remainder of case (i) can be described as follows:
Since ![]() $S^{\boldsymbol {i}}_x$ commutes with
$S^{\boldsymbol {i}}_x$ commutes with ![]() $M^{\boldsymbol {i}}[x',y']$ and
$M^{\boldsymbol {i}}[x',y']$ and ![]() $M^{\boldsymbol {i}}[x',y'_-]$ by [Reference Kashiwara, Kim, Oh and ParkKKOP21, Proposition 3.27],
$M^{\boldsymbol {i}}[x',y'_-]$ by [Reference Kashiwara, Kim, Oh and ParkKKOP21, Proposition 3.27],
 \begin{align*} \Lambda(S^{\boldsymbol{i}}_x,M^{\boldsymbol{i}}[x',y']) & = - \Lambda(M^{\boldsymbol{i}}[x',y'],S^{\boldsymbol{i}}_x) = -\Lambda( S^{\boldsymbol{i}}_{y'} \triangledown M^{\boldsymbol{i}}[x',y'_-],S^{\boldsymbol{i}}_x) \\ & = -\Lambda( S^{\boldsymbol{i}}_{y'} ,S^{\boldsymbol{i}}_x) -\Lambda( M^{\boldsymbol{i}}[x',y'_-],S^{\boldsymbol{i}}_x) \\ & = ({\mspace{1mu}\beta}_{y'},{\mspace{1mu}\beta}_x) + \Lambda( S^{\boldsymbol{i}}_x, M^{\boldsymbol{i}}[x',y'_-]) = \lambda^{\boldsymbol{i}}_{x,y'} + \Lambda( S^{\boldsymbol{i}}_x, M^{\boldsymbol{i}}[x',y'_-]), \end{align*}
\begin{align*} \Lambda(S^{\boldsymbol{i}}_x,M^{\boldsymbol{i}}[x',y']) & = - \Lambda(M^{\boldsymbol{i}}[x',y'],S^{\boldsymbol{i}}_x) = -\Lambda( S^{\boldsymbol{i}}_{y'} \triangledown M^{\boldsymbol{i}}[x',y'_-],S^{\boldsymbol{i}}_x) \\ & = -\Lambda( S^{\boldsymbol{i}}_{y'} ,S^{\boldsymbol{i}}_x) -\Lambda( M^{\boldsymbol{i}}[x',y'_-],S^{\boldsymbol{i}}_x) \\ & = ({\mspace{1mu}\beta}_{y'},{\mspace{1mu}\beta}_x) + \Lambda( S^{\boldsymbol{i}}_x, M^{\boldsymbol{i}}[x',y'_-]) = \lambda^{\boldsymbol{i}}_{x,y'} + \Lambda( S^{\boldsymbol{i}}_x, M^{\boldsymbol{i}}[x',y'_-]), \end{align*}
then our assertion follows from the induction hypothesis on ![]() $|\,[x',y']_{\boldsymbol {i}}|$.
$|\,[x',y']_{\boldsymbol {i}}|$.
(ii) [![]() $x< y$] Assume first that
$x< y$] Assume first that ![]() $y>y'$. Then we have
$y>y'$. Then we have
 \begin{align*} \Lambda(M^{\boldsymbol{i}}[x,y],M^{\boldsymbol{i}}[x',y']) & = \Lambda(S^{\boldsymbol{i}}_y \triangledown M^{\boldsymbol{i}}[x,y_-],M^{\boldsymbol{i}}[x',y']) \\ & = \Lambda(S^{\boldsymbol{i}}_y,M^{\boldsymbol{i}}[x',y']) + \Lambda(M^{\boldsymbol{i}}[x,y_-],M^{\boldsymbol{i}}[x',y']). \end{align*}
\begin{align*} \Lambda(M^{\boldsymbol{i}}[x,y],M^{\boldsymbol{i}}[x',y']) & = \Lambda(S^{\boldsymbol{i}}_y \triangledown M^{\boldsymbol{i}}[x,y_-],M^{\boldsymbol{i}}[x',y']) \\ & = \Lambda(S^{\boldsymbol{i}}_y,M^{\boldsymbol{i}}[x',y']) + \Lambda(M^{\boldsymbol{i}}[x,y_-],M^{\boldsymbol{i}}[x',y']). \end{align*}
Note that ![]() $(S^{\boldsymbol {i}}_y,M^{\boldsymbol {i}}[x',y'])$ is an unmixed pair. Then, by induction on
$(S^{\boldsymbol {i}}_y,M^{\boldsymbol {i}}[x',y'])$ is an unmixed pair. Then, by induction on ![]() $|[x,y]_{\boldsymbol {i}}|$, we have
$|[x,y]_{\boldsymbol {i}}|$, we have
 \begin{align*} \Lambda(M^{\boldsymbol{i}}[x,y],M^{\boldsymbol{i}}[x',y'])& = \Lambda(S^{\boldsymbol{i}}_y \triangledown M^{\boldsymbol{i}}[x,y_-],M^{\boldsymbol{i}}[x',y'])\\ & = \sum_{v \in [x',y']_{\boldsymbol{i}}} \lambda^{\boldsymbol{i}}_{y,v} + \sum_{ u \in [x,y_-]_{\boldsymbol{i}}; \ v \in [x',y']_{\boldsymbol{i}} } \lambda^{\boldsymbol{i}}_{u,v}, \end{align*}
\begin{align*} \Lambda(M^{\boldsymbol{i}}[x,y],M^{\boldsymbol{i}}[x',y'])& = \Lambda(S^{\boldsymbol{i}}_y \triangledown M^{\boldsymbol{i}}[x,y_-],M^{\boldsymbol{i}}[x',y'])\\ & = \sum_{v \in [x',y']_{\boldsymbol{i}}} \lambda^{\boldsymbol{i}}_{y,v} + \sum_{ u \in [x,y_-]_{\boldsymbol{i}}; \ v \in [x',y']_{\boldsymbol{i}} } \lambda^{\boldsymbol{i}}_{u,v}, \end{align*}
which yields our assertion for this case.
Now let us assume that ![]() $y \leqslant y'$. Then we have
$y \leqslant y'$. Then we have
Then for any ![]() $u \in [x,y]_{\boldsymbol {i}}$,
$u \in [x,y]_{\boldsymbol {i}}$, ![]() $S^{\boldsymbol {i}}_u$ commutes with
$S^{\boldsymbol {i}}_u$ commutes with ![]() $M^{\boldsymbol {i}}[x',y']$ by [Reference Kashiwara, Kim, Oh and ParkKKOP21, Proposition 3.27]. By [Reference Kang, Kashiwara, Kim and OhKKKO18, Proposition 3.2.13], we have
$M^{\boldsymbol {i}}[x',y']$ by [Reference Kashiwara, Kim, Oh and ParkKKOP21, Proposition 3.27]. By [Reference Kang, Kashiwara, Kim and OhKKKO18, Proposition 3.2.13], we have
Then our assertion follows from case (i).
We say that ![]() ${\boldsymbol {i}}$-boxes
${\boldsymbol {i}}$-boxes ![]() $[a_1,b_1]$ and
$[a_1,b_1]$ and ![]() $[a_2,b_2]$ commute if we have either
$[a_2,b_2]$ commute if we have either
The following corollary is proved in [Reference Kashiwara, Kim, Oh and ParkKKOP24b, Theorem 4.21] in the quantum affine case.
Corollary 5.8 For commuting ![]() ${\boldsymbol {i}}$-boxes
${\boldsymbol {i}}$-boxes ![]() $[a_1,b_1]$ and
$[a_1,b_1]$ and ![]() $[a_2,b_2]$, the modules
$[a_2,b_2]$, the modules ![]() $M^{\boldsymbol {i}}[a_1,b_1]$ and
$M^{\boldsymbol {i}}[a_1,b_1]$ and ![]() $M^{\boldsymbol {i}}[a_2,b_2]$ commute.
$M^{\boldsymbol {i}}[a_2,b_2]$ commute.
Proof. By Proposition 5.7, we have
 \[ \Lambda(M^{\boldsymbol{i}}[a_1,b_1],M^{\boldsymbol{i}}[a_2,b_2]) = \sum_{\substack{u \in [a_1,b_1]_{\boldsymbol{i}} \\ v \in [a_2,b_2]_{\boldsymbol{i}} }} \lambda^{\boldsymbol{i}}_{u,v} = - \Lambda(M^{\boldsymbol{i}}[a_2,b_2],M^{\boldsymbol{i}}[a_1,b_1]), \]
\[ \Lambda(M^{\boldsymbol{i}}[a_1,b_1],M^{\boldsymbol{i}}[a_2,b_2]) = \sum_{\substack{u \in [a_1,b_1]_{\boldsymbol{i}} \\ v \in [a_2,b_2]_{\boldsymbol{i}} }} \lambda^{\boldsymbol{i}}_{u,v} = - \Lambda(M^{\boldsymbol{i}}[a_2,b_2],M^{\boldsymbol{i}}[a_1,b_1]), \]
which implies ![]() $\mathfrak {d}(M^{\boldsymbol {i}}[a_1,b_1],M^{\boldsymbol {i}}[a_2,b_2])=0$. Thus, our assertion follows from Proposition 2.7(v).
$\mathfrak {d}(M^{\boldsymbol {i}}[a_1,b_1],M^{\boldsymbol {i}}[a_2,b_2])=0$. Thus, our assertion follows from Proposition 2.7(v).
Proposition 5.9 For a commuting pair ![]() $(M^{\boldsymbol {i}}[x,y],M^{\boldsymbol {i}}[x',y'])$, (5.6) holds.
$(M^{\boldsymbol {i}}[x,y],M^{\boldsymbol {i}}[x',y'])$, (5.6) holds.
Proof. If the ![]() ${\boldsymbol {i}}$-boxes
${\boldsymbol {i}}$-boxes ![]() $[x,y]$ and
$[x,y]$ and ![]() $[x',y']$ satisfy (5.5), our assertion holds. Thus, it is enough to consider when
$[x',y']$ satisfy (5.5), our assertion holds. Thus, it is enough to consider when ![]() $x \leqslant x'_-$ and
$x \leqslant x'_-$ and ![]() $y_+ \leqslant y'$. Since they commute,
$y_+ \leqslant y'$. Since they commute,
If ![]() $x'> x_-$ or
$x'> x_-$ or ![]() $y'_+> y$, Proposition 5.7 says that
$y'_+> y$, Proposition 5.7 says that
which implies the assertion. Thus, we may assume that ![]() $x' \leqslant x_-$. However, in this case, we have
$x' \leqslant x_-$. However, in this case, we have
which yields a contradiction.
Let us define the skew-symmetric pairing ![]() ${\mathrm L}_{\boldsymbol {i}}$ on
${\mathrm L}_{\boldsymbol {i}}$ on ![]() ${\rm Irr}(\mathscr {C}_w)$ as follows:
${\rm Irr}(\mathscr {C}_w)$ as follows:
The following lemma follows from Lemma 4.1 and (5.7).
Lemma 5.10 For ![]() $M=\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})$ with
$M=\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})$ with ![]() $\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^{\mathsf {K}}$, we have
$\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\ge 0}^{\mathsf {K}}$, we have
Proposition 5.11 For any simple ![]() $X,Y$ in
$X,Y$ in ![]() $\mathscr {C}_w$, we have
$\mathscr {C}_w$, we have
Proof. Let ![]() $\mathcal {S}$ be the set of simple modules
$\mathcal {S}$ be the set of simple modules ![]() $Y$ in
$Y$ in ![]() $\mathscr {C}_w$ such that
$\mathscr {C}_w$ such that ![]() ${\mathrm L}_{\boldsymbol {i}}(X,Y)={\mathrm G}^R_{\mathcal {M}^{\boldsymbol {i}}}(X,Y)$ for any simple
${\mathrm L}_{\boldsymbol {i}}(X,Y)={\mathrm G}^R_{\mathcal {M}^{\boldsymbol {i}}}(X,Y)$ for any simple ![]() $X\in \mathscr {C}_w$, and let
$X\in \mathscr {C}_w$, and let ![]() $\mathcal {S}'$ be the set of simple modules
$\mathcal {S}'$ be the set of simple modules ![]() $Y$ in
$Y$ in ![]() $\mathscr {C}_w$ such that
$\mathscr {C}_w$ such that ![]() ${\mathrm L}_{\boldsymbol {i}}(\mathcal {M}^{\boldsymbol {i}}(\mathbf {a}),Y)={\mathrm G}^R_{\mathcal {M}^{\boldsymbol {i}}}(\mathcal {M}^{\boldsymbol {i}}(\mathbf {a}),Y)$ for any
${\mathrm L}_{\boldsymbol {i}}(\mathcal {M}^{\boldsymbol {i}}(\mathbf {a}),Y)={\mathrm G}^R_{\mathcal {M}^{\boldsymbol {i}}}(\mathcal {M}^{\boldsymbol {i}}(\mathbf {a}),Y)$ for any ![]() $\mathbf {a}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K}$. By Proposition 5.9, we have
$\mathbf {a}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K}$. By Proposition 5.9, we have
Thus, we have ![]() $\mathcal {M}^{\boldsymbol {i}}(\mathbf {a}) \in \mathcal {S}'$ by Lemma 5.10. Now, let us show
$\mathcal {M}^{\boldsymbol {i}}(\mathbf {a}) \in \mathcal {S}'$ by Lemma 5.10. Now, let us show ![]() $\mathcal {S}'\subset \mathcal {S}$. Let
$\mathcal {S}'\subset \mathcal {S}$. Let ![]() $Y\in \mathcal {S}'$. For any simple
$Y\in \mathcal {S}'$. For any simple ![]() $X$, there exist
$X$, there exist ![]() $\mathbf {a},\mathbf {b}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K}$ such that
$\mathbf {a},\mathbf {b}\in \mathbb {Z}\mspace {1mu}_{\ge 0}^\mathsf {K}$ such that ![]() $X\triangledown \mathcal {M}^{\boldsymbol {i}}(\mathbf {a})\simeq \mathcal {M}^{\boldsymbol {i}}(\mathbf {b})$. Hence, we have
$X\triangledown \mathcal {M}^{\boldsymbol {i}}(\mathbf {a})\simeq \mathcal {M}^{\boldsymbol {i}}(\mathbf {b})$. Hence, we have
 \begin{align*} {\mathrm
L}_{\boldsymbol{i}}(X,Y)+{\mathrm
L}_{\boldsymbol{i}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{a}),Y)&\underset{(1)}={\mathrm
L}_{\boldsymbol{i}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{b}),Y)=
{\mathrm
G}^R_{\mathcal{M}^{\boldsymbol{i}}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{b}),Y)\\
&\underset{(2)}={\mathrm
G}^R_{\mathcal{M}^{\boldsymbol{i}}}(X,Y)+{\mathrm
G}^R_{\mathcal{M}^{\boldsymbol{i}}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{a}),Y)=
{\mathrm
G}^R_{\mathcal{M}^{\boldsymbol{i}}}(X,Y)+{\mathrm
L}_{\boldsymbol{i}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{a}),Y).
\end{align*}
\begin{align*} {\mathrm
L}_{\boldsymbol{i}}(X,Y)+{\mathrm
L}_{\boldsymbol{i}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{a}),Y)&\underset{(1)}={\mathrm
L}_{\boldsymbol{i}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{b}),Y)=
{\mathrm
G}^R_{\mathcal{M}^{\boldsymbol{i}}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{b}),Y)\\
&\underset{(2)}={\mathrm
G}^R_{\mathcal{M}^{\boldsymbol{i}}}(X,Y)+{\mathrm
G}^R_{\mathcal{M}^{\boldsymbol{i}}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{a}),Y)=
{\mathrm
G}^R_{\mathcal{M}^{\boldsymbol{i}}}(X,Y)+{\mathrm
L}_{\boldsymbol{i}}(\mathcal{M}^{\boldsymbol{i}}(\mathbf{a}),Y).
\end{align*}
Here ![]() $\underset {(1)}=$ follows from Lemma 5.10 and
$\underset {(1)}=$ follows from Lemma 5.10 and ![]() $\underset {(2)}=$ follows from Lemma 5.1. Hence, we have
$\underset {(2)}=$ follows from Lemma 5.1. Hence, we have ![]() ${\mathrm L}_{\boldsymbol {i}}(X,Y)={\mathrm G}^R_{\mathcal {M}^{\boldsymbol {i}}}(X,Y)$. Thus, we have proved
${\mathrm L}_{\boldsymbol {i}}(X,Y)={\mathrm G}^R_{\mathcal {M}^{\boldsymbol {i}}}(X,Y)$. Thus, we have proved ![]() $\mathcal {S}'\subset \mathcal {S}$.
$\mathcal {S}'\subset \mathcal {S}$.
Since ![]() $\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})\in \mathcal {S}'$, we have
$\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})\in \mathcal {S}'$, we have ![]() $\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})\in \mathcal {S}$, which implies that
$\mathcal {M}^{\boldsymbol {i}}(\mathbf {a})\in \mathcal {S}$, which implies that
for any simple ![]() $Y$. Hence any simple
$Y$. Hence any simple ![]() $Y$ belongs to
$Y$ belongs to ![]() $\mathcal {S}'$ and hence to
$\mathcal {S}'$ and hence to ![]() $\mathcal {S}$.
$\mathcal {S}$.
5.3 Degree and codegree
In this subsection, we see the relationship between ![]() $\mathbf {g}^R_\mathcal {M}(X)$ (respectively,
$\mathbf {g}^R_\mathcal {M}(X)$ (respectively, ![]() $\mathbf {g}^L_\mathcal {M}(X)$) and the degree (respectively, codegree) in the (quantum) cluster algebra theory. For a commuting family
$\mathbf {g}^L_\mathcal {M}(X)$) and the degree (respectively, codegree) in the (quantum) cluster algebra theory. For a commuting family ![]() $\mathcal {M}=\{ M_j \mid j \in J \}$ labeled by a finite index set
$\mathcal {M}=\{ M_j \mid j \in J \}$ labeled by a finite index set ![]() $J$, let us recall the preorder
$J$, let us recall the preorder ![]() $\preccurlyeq _\mathcal {M}$ on
$\preccurlyeq _\mathcal {M}$ on ![]() $\mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ given in [Reference Kashiwara and KimKK19, § 3.3] (see also [Reference QinQin17, Definition 3.1.1]):
$\mathbb {Z}\mspace {1mu}_{\geqslant 0}^{J}$ given in [Reference Kashiwara and KimKK19, § 3.3] (see also [Reference QinQin17, Definition 3.1.1]):
The preorder ![]() $\preccurlyeq _\mathcal {M}$ can be extended to the one on
$\preccurlyeq _\mathcal {M}$ can be extended to the one on ![]() $\mathbb {Z}\mspace {1mu}^{J}$ as follows: for
$\mathbb {Z}\mspace {1mu}^{J}$ as follows: for ![]() $\mathbf {b},\mathbf {b}' \in \mathbb {Z}\mspace {1mu}^{J}$,
$\mathbf {b},\mathbf {b}' \in \mathbb {Z}\mspace {1mu}^{J}$,
We write ![]() $\mathbf {b}'\prec _\mathcal {M}\mathbf {b}$, if
$\mathbf {b}'\prec _\mathcal {M}\mathbf {b}$, if ![]() $\mathbf {b}'\preccurlyeq _\mathcal {M}\mathbf {b}$ holds but
$\mathbf {b}'\preccurlyeq _\mathcal {M}\mathbf {b}$ holds but ![]() $\mathbf {b}\preccurlyeq _\mathcal {M}\mathbf {b}'$ does not hold. Hence,
$\mathbf {b}\preccurlyeq _\mathcal {M}\mathbf {b}'$ does not hold. Hence, ![]() $\mathbf {b}'\prec _\mathcal {M}\mathbf {b}$ if and only if
$\mathbf {b}'\prec _\mathcal {M}\mathbf {b}$ if and only if ![]() $\mathbf {b}'\preccurlyeq _\mathcal {M}\mathbf {b}$ and there exists
$\mathbf {b}'\preccurlyeq _\mathcal {M}\mathbf {b}$ and there exists ![]() $j\in J$ such that
$j\in J$ such that ![]() $\Lambda (\mathcal {M}(\mathbf {b}),M_j)<\Lambda (\mathcal {M}(\mathbf {b}'),M_j)$.
$\Lambda (\mathcal {M}(\mathbf {b}),M_j)<\Lambda (\mathcal {M}(\mathbf {b}'),M_j)$.
Lemma 5.12 (cf. [Reference Kashiwara and KimKK19, Lemma 3.6])
Let ![]() $X$ be a simple module and
$X$ be a simple module and ![]() $\mathcal {M}=\{ M_j \mid j \in J\}$ be a quasi-Laurent family in
$\mathcal {M}=\{ M_j \mid j \in J\}$ be a quasi-Laurent family in ![]() $\mathscr {C}$. Let
$\mathscr {C}$. Let ![]() $\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}$,
$\mathbf {a} \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}$, ![]() $\mathsf {S}$,
$\mathsf {S}$, ![]() $c(s) \in \mathbb {Z}\mspace {1mu}$ and
$c(s) \in \mathbb {Z}\mspace {1mu}$ and ![]() $\mathbf {b}(s) \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^J$
$\mathbf {b}(s) \in \mathbb {Z}\mspace {1mu}_{\geqslant 0}^J$ ![]() $(s \in \mathsf {S})$ be as in (3.1). Then we have the following.
$(s \in \mathsf {S})$ be as in (3.1). Then we have the following.
(i) There exists a unique
 $s_0 \in \mathsf {S}$ such that
$s_0 \in \mathsf {S}$ such that  $X \triangledown \mathcal {M}(\mathbf {a}) \simeq q^{\,c(s_0)} \mathcal {M}(\mathbf {b}(s_0))$. Moreover, we have
$X \triangledown \mathcal {M}(\mathbf {a}) \simeq q^{\,c(s_0)} \mathcal {M}(\mathbf {b}(s_0))$. Moreover, we have  $\mathbf {b}(s) \prec _\mathcal {M} \mathbf {b}(s_0)$ for any
$\mathbf {b}(s) \prec _\mathcal {M} \mathbf {b}(s_0)$ for any  $s \in \mathsf {S} \setminus \{ s_0 \}$.
$s \in \mathsf {S} \setminus \{ s_0 \}$.(ii) There exists a unique
 $s_1 \in \mathsf {S}$ such that
$s_1 \in \mathsf {S}$ such that  $X \triangle \mathcal {M}(\mathbf {a}) \simeq q^{\,c(s_1)} \mathcal {M}(\mathbf {b}(s_1))$. Moreover, we have
$X \triangle \mathcal {M}(\mathbf {a}) \simeq q^{\,c(s_1)} \mathcal {M}(\mathbf {b}(s_1))$. Moreover, we have  $\mathbf {b}(s_1) \prec _\mathcal {M} \mathbf {b}(s)$ for any
$\mathbf {b}(s_1) \prec _\mathcal {M} \mathbf {b}(s)$ for any  $s \in \mathsf {S} \setminus \{ s_1 \}$.
$s \in \mathsf {S} \setminus \{ s_1 \}$.(iii) If
 $s_0 = s_1$, then
$s_0 = s_1$, then  $\mathsf {S} = \{ s_0\}$ and
$\mathsf {S} = \{ s_0\}$ and  $X \circ \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b}(s_0))$.
$X \circ \mathcal {M}(\mathbf {a}) \simeq \mathcal {M}(\mathbf {b}(s_0))$.(iv) If
 $s_0 \ne s_1$ and there exists no
$s_0 \ne s_1$ and there exists no  $\mathbf {c} \in \mathbb {Z}\mspace {1mu}^\mathsf {K}$ such that
$\mathbf {c} \in \mathbb {Z}\mspace {1mu}^\mathsf {K}$ such that  $\mathbf {b}(s_1) - \mathbf {a} \prec _\mathcal {M} \mathbf {c} \prec _\mathcal {M} \mathbf {b}(s_0) - \mathbf {a}$, then
$\mathbf {b}(s_1) - \mathbf {a} \prec _\mathcal {M} \mathbf {c} \prec _\mathcal {M} \mathbf {b}(s_0) - \mathbf {a}$, then
 \[ [X \circ \mathcal{M}(\mathbf{a})] = [X \triangledown \mathcal{M}(\mathbf{a})] + [X \triangle \mathcal{M}(\mathbf{a})] \quad \text{in $K(\mathscr{C}_w)$.} \]
\[ [X \circ \mathcal{M}(\mathbf{a})] = [X \triangledown \mathcal{M}(\mathbf{a})] + [X \triangle \mathcal{M}(\mathbf{a})] \quad \text{in $K(\mathscr{C}_w)$.} \]
The following proposition is proved for symmetric quiver Hecke algebras and can be extended to general quiver Hecke algebras using almost the same argument:
Proposition 5.13 [Reference Kashiwara and KimKK19, Proposition 3.3]
For a monoidal cluster ![]() $\mathcal {M}=\{ M_k \mid k \in \mathsf {K}\}$ associated with a quantum seed
$\mathcal {M}=\{ M_k \mid k \in \mathsf {K}\}$ associated with a quantum seed ![]() $(\{ X_k\}_{k\in \mathsf {K}}, L,\widetilde {B})$,
$(\{ X_k\}_{k\in \mathsf {K}}, L,\widetilde {B})$,
In particular, the relation ![]() $\preccurlyeq _\mathcal {M}$ is an order on
$\preccurlyeq _\mathcal {M}$ is an order on ![]() $\mathbb {Z}\mspace {1mu}^\mathsf {K}$.
$\mathbb {Z}\mspace {1mu}^\mathsf {K}$.
Corollary 5.14 Let ![]() $\mathcal {M}=\{ M_k \mid k \in \mathsf {K}\}$ be a monoidal cluster associated with a quantum seed
$\mathcal {M}=\{ M_k \mid k \in \mathsf {K}\}$ be a monoidal cluster associated with a quantum seed ![]() $\mathcal {S}=( \{X_k\}_{k \in \mathsf {K}}, L, B)$. Then
$\mathcal {S}=( \{X_k\}_{k \in \mathsf {K}}, L, B)$. Then ![]() $[X]$ is
$[X]$ is ![]() $\mathcal {T}(L)$-pointed and
$\mathcal {T}(L)$-pointed and ![]() $\mathcal {T}(L)$-copointed for any simple module
$\mathcal {T}(L)$-copointed for any simple module ![]() $X \in \mathscr {C}_w$.
$X \in \mathscr {C}_w$.
Remark 5.15 For a monoidal cluster ![]() $\mathcal {M}$ associated with a quantum seed
$\mathcal {M}$ associated with a quantum seed ![]() $\mathcal {S}$ and a simple module
$\mathcal {S}$ and a simple module ![]() $M \in \mathscr {C}$, the above corollary says that
$M \in \mathscr {C}$, the above corollary says that ![]() $\mathbf {g}^R_\mathcal {M}(M)$ and
$\mathbf {g}^R_\mathcal {M}(M)$ and ![]() $\mathbf {g}^L_\mathcal {M}(M)$ coincide with the degree and codegree of
$\mathbf {g}^L_\mathcal {M}(M)$ coincide with the degree and codegree of ![]() $[M] \in \mathcal {K}_\mathbb {A}(\mathscr {C}) \simeq \mathscr {A}_\mathbb {A}(\mathcal {S})$, respectively.
$[M] \in \mathcal {K}_\mathbb {A}(\mathscr {C}) \simeq \mathscr {A}_\mathbb {A}(\mathcal {S})$, respectively.
Acknowledgements
The second, third and fourth authors gratefully acknowledge the hospitality of RIMS (Kyoto University) during their visit in 2023. The authors would like to thank the referee for reading our manuscript carefully and making constructive comments.
Conflicts of interest
None.
Financial support
The research of M. Kashiwara was supported by Grant-in-Aid for Scientific Research (B) 23K20206, Japan Society for the Promotion of Science. The research of M. Kim was supported by the National Research Foundation of Korea (NRF) Grant funded by the Korea government (MSIT) (NRF-2022R1F1A1076214 and NRF-2020R1A5A1016126). The research of S.-j. Oh was supported by the National Research Foundation of Korea (NRF) Grant funded by the Korea government (MSIT) (NRF-2022R1A2C1004045). The research of E. Park was supported by the National Research Foundation of Korea (NRF) Grant funded by the Korea Government (MSIT) (RS-2023-00273425 and NRF-2020R1A5A1016126).
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.