Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kumagai, Takashi
and
Misumi, Jun
2008.
Heat Kernel Estimates for Strongly Recurrent Random Walk on Random Media.
Journal of Theoretical Probability,
Vol. 21,
Issue. 4,
p.
910.
Biskup, Marek
2011.
Graph diameter in long‐range percolation.
Random Structures & Algorithms,
Vol. 39,
Issue. 2,
p.
210.
Crawford, Nicholas
and
Sly, Allan
2012.
Simple random walk on long range percolation clusters I: heat kernel bounds.
Probability Theory and Related Fields,
Vol. 154,
Issue. 3-4,
p.
753.
Crawford, Nicholas
and
Sly, Allan
2013.
Simple random walk on long-range percolation clusters II: Scaling limits.
The Annals of Probability,
Vol. 41,
Issue. 2,
Misumi, Jun
2015.
The Diameter of a Long-Range Percolation Cluster on Pre-Sierpinski Gasket.
Journal of Statistical Physics,
Vol. 158,
Issue. 5,
p.
1083.
Amir, Gideon
Angel, Omer
Benjamini, Itai
and
Kozma, Gady
2016.
One-dimensional long-range diffusion-limited aggregation I.
The Annals of Probability,
Vol. 44,
Issue. 5,
Chatterjee, Shirshendu
and
S. Dey, Partha
2016.
Multiple Phase Transitions in Long‐Range First‐Passage Percolation on Square Lattices.
Communications on Pure and Applied Mathematics,
Vol. 69,
Issue. 2,
p.
203.
Misumi, Jun
2016.
The Mixing Time of a Random Walk on a Long-Range Percolation Cluster in Pre-Sierpinski Gasket.
Journal of Statistical Physics,
Vol. 165,
Issue. 1,
p.
153.
Biskup, Marek
and
Lin, Jeffrey
2019.
Sharp asymptotic for the chemical distance in long‐range percolation.
Random Structures & Algorithms,
Vol. 55,
Issue. 3,
p.
560.
Dyer, Martin E.
Galanis, Andreas
Goldberg, Leslie Ann
Jerrum, Mark
and
Vigoda, Eric
2020.
Random Walks on Small World Networks.
ACM Transactions on Algorithms,
Vol. 16,
Issue. 3,
p.
1.
Hutchcroft, Tom
2023.
Transience and anchored isoperimetric dimension of supercritical percolation clusters.
Electronic Journal of Probability,
Vol. 28,
Issue. none,
Bäumler, Johannes
2023.
Recurrence and transience of symmetric random walks with long-range jumps.
Electronic Journal of Probability,
Vol. 28,
Issue. none,
Cipriani, Alessandra
and
Salvi, Michele
2024.
Scale-free percolation mixing time.
Stochastic Processes and their Applications,
Vol. 167,
Issue. ,
p.
104236.
Biskup, Marek
and
Krieger, Andrew
2024.
Arithmetic oscillations of the chemical distance in long-range percolation on Zd.
The Annals of Applied Probability,
Vol. 34,
Issue. 3,


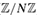 ). While it is known that the asymptotic almost sure diameter drops from linear to poly-logarithmic as the exponent
). While it is known that the asymptotic almost sure diameter drops from linear to poly-logarithmic as the exponent 