Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-20T00:42:29.402Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of the Coefficients of Orthonormal Sequences

Published online by Cambridge University Press:  20 November 2018

P. S. Bullen
P. S. Bullen*
Affiliation:
University of British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider complete orthonormal sequences defined on the interval [0, 1] and satisfying an inequality of the type

(1)

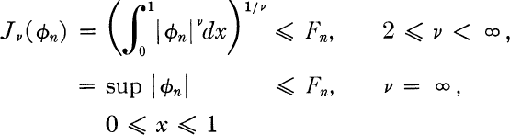
for all n and some sequence {Fn}. Such sequences were first considered by Zygmund and Marcinkiewicz (8). They extended the well-known results of Hausdorff-Young and Paley, originally proved for the case v = ∞, Fn = M for all n (12). We will consider cases of equality in t he Hausdorff-Young theorems and certain limiting cases of the Paley theorems. Application of these results and the results in (8) will be made to functions harmonic in the unit α-sphere.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 13 , 1961 , pp. 305 - 315
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. Calderôn, A. P. and Zygmund, A., On the theorem of Hausdorff- Young and its extensions, Ann. Math. Studies No. 25.Google Scholar
2. du Plessis, N., Some theorems about the Riesz fractional integral, Trans. Amer. Math. Soc, 80 (1955), 124–134.Google Scholar
3. du Plessis, N., Spherical Fejér-Riesz theorems, J. London Math. Soc, 31 (1956), 386–91.Google Scholar
4. Hardy, G. H. and Littlewood, J. E., Some new properties of Fourier constants, Math. Annalen, 97 (1926), 159–209.Google Scholar
5. Hardy, G. H. and Littlewood, J. E., Some properties of fractional integrals II, Math. Zeitschrift, 34 (1931), 403–439.Google Scholar
6. Kacmarz, S. and Steinhaus, H., Théorie der Orthogonalreihen (Chelsea, 1951).Google Scholar
7. Littlewood, J. E., On a theorem of Paley, J. London Math. Soc, 29 (1954), 387–395.Google Scholar
8. Marcinkiewicz, J. and Zygmund, A., Some theorems on orthogonal systems, Fund. Math., 28 (1957), 309–335.Google Scholar
9. Mullholland, H. P., Concerning the generalization of the Young-Hausdorff theorem, Proc London Math. Soc, 35 (1933), 257–293.Google Scholar
10. Verblunsky, S., Fourier constants and Lebesgue classes, Proc. London Math. Soc, 24 (1935), 1–31.Google Scholar
11. Zygmund, A., Some points in the theory of trigonometric series and power series, Trans. Amer. Math. Soc, 36 (1934), 586–617.Google Scholar
12. Zygmund, A., Trigonometric series (2nd ed.; Cambridge, 1959) I, II.Google Scholar