Hostname: page-component-77c89778f8-gq7q9 Total loading time: 0 Render date: 2024-07-16T09:53:05.718Z Has data issue: false hasContentIssue false
  • English
  • Français

On Whitney-type Characterization of Approximate Differentiability on Metric Measure Spaces

Published online by Cambridge University Press:  20 November 2018

E. Durand-Cartagena ,
L. Ihnatsyeva ,
R. Korte  and
M. Szumańska
E. Durand-Cartagena
Affiliation:
Departamento de Matemática Aplicada, ETSI Industriales, UNED c/Juan del Rosal 12 Ciudad Universitaria, 28040 Madrid, Spain. e-mail: [email protected]
L. Ihnatsyeva
Affiliation:
Department of Mathematics and Statistics, P.O. Box 68, FI-00014 University of Helsinki, Finland. e-mail: [email protected], [email protected]
R. Korte
Affiliation:
Department of Mathematics and Statistics, P.O. Box 68, FI-00014 University of Helsinki, Finland. e-mail: [email protected], [email protected]
M. Szumańska
Affiliation:
Faculty of Mathematics, Informatics, and Mechanics University of Warsaw, Banacha 2, 02-097 Warszawa, Poland. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study approximately differentiable functions on metric measure spaces admitting a Cheeger differentiable structure. The main result is a Whitney-type characterization of approximately differentiable functions in this setting. As an application, we prove a Stepanov-type theorem and consider approximate differentiability of Sobolev, 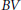$BV$, and maximal functions.

Keywords

26B0528A1528A7546E35approximate differentiabilitymetric spacestrong measurable differentiable structure, Whitney theorem
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 4 , 01 August 2014 , pp. 721 - 742
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

The first author was partially supported by grant MTM2009-07848 (Spain). The second, the third and the fourth authors were supported by the Academy of Finland (grants 252293, 250403 and 138738). The fourth author was partially supported by MNiSW Grant no N N201 397737, Nonlinear partial differential equations: geometric and variational problems.

References

[1] Aalto, D. and Kinnunen, J., The discrete maximal operator in metric spaces. J. Anal. Math. 111(2010), 369–390. http://dx.doi.org/10.1007/s11854-010-0022-3 CrossRefGoogle Scholar
[2] Aalto, D., Maximal functions in Sobolev spaces. In: Sobolev spaces in mathematics. I, Int. Math. Ser. (N. Y.), 8, Springer, New York, 2009, pp. 25–67.Google Scholar
[3] Ambrosio, L. and Tilli, P., Topics on analysis in metric spaces. Oxford Lecture Series in Mathematics and its Applications, 25, Oxford University Press, Oxford, 2004.Google Scholar
[4] Balogh, Z. M., Rogovin, K., and Zürcher, T., The Stepanov differentiability theorem in metric measure spaces. J. Geom. Anal. 14(2004), no. 3, 405–422. http://dx.doi.org/10.1007/BF02922098 CrossRefGoogle Scholar
[5] Basalaev, S. G.and Vodopyanov, S. K., Approximate differentiability of mappings of Carnot-Carathéodory spaces. 2012. http://arxiv:1206.5197 Google Scholar
[6] Bate, D. and Speight, G., Differentiability, porosity and doubling in metric measure spaces. Proc. Amer. Math. Soc. 141(2013), no. 3, 971–985. http://dx.doi.org/10.1090/S0002-9939-2012-11457-1 CrossRefGoogle Scholar
[7] Björn, A. and Björn, J., Nonlinear potential theory on metric spaces. EMS Tracts in Mathematics, 17, European Mathematical Society, Zürich, 2011.Google Scholar
[8] Björn, A., Björn, J., and Shanmugalingam, N., The Dirichlet problem for p-harmonic functions on metric spaces. J. Reine Angew. Math. 556(2003), 173–203.Google Scholar
[9] Björn, J., Lq-differentials for weighted Sobolev spaces. Michigan Math. J. 47(2000), no. 1, 151–161. http://dx.doi.org/10.1307/mmj/1030374674 CrossRefGoogle Scholar
[10] Bojarski, B., Differentiation of measurable functions and Whitney-Luzin type structure theorems. Helsinki University of Technology Institute of Mathematics Research Reports, 2009.Google Scholar
[11] Buckley, S. M., Is the maximal function of a Lipschitz function continuous? Ann. Acad. Sci. Fenn. Math. 24(1999), no. 2, 519–528.Google Scholar
[12] Cheeger, J., Differentiability of Lipschitz Functions on metric measure spaces. Geom. Funct. Anal. 9(1999), no. 3, 428–517. http://dx.doi.org/10.1007/s000390050094 CrossRefGoogle Scholar
[13] Denjoy, A., Sur les fonctions dérivées sommables. Bull. Soc. Math. France 43(1915), 161–248.CrossRefGoogle Scholar
[14] Durand-Cartagena, E., Jaramillo, J. A., andShanmugalingam, N., The∞-Poincaréinequality in metric measure spaces. Michigan Math. J. 61(2012), no. 1, 63–85. http://dx.doi.org/10.1307/mmj/1331222847 CrossRefGoogle Scholar
[15] Evans, L. C. and Gariepy, R. F., Measure theory and fine properties of functions. Studies in Advanced Mathematics, CRC Press, Boca Raton, FL, 1992.Google Scholar
[16] Federer, H., Geometric measure theory. Die Grundlehren der mathematischenWissenschaften, 153, Springer-Verlag New York Inc., New York, 1969.Google Scholar
[17] Hajłasz, P., Sobolev spaces on metric-measure spaces. In: Heat kernels and analysis on manifolds, graphs, and metric spaces (Paris, 2002), Contemp. Math., 338, Amer. Math. Soc., Providence, RI, 2003, pp. 173–218.Google Scholar
[18] Hajłasz, P. and Koskela, P., Sobolev met Poincaré. Mem. Amer. Math. Soc. 145(2000), no. 688.Google Scholar
[19] Hajłasz, P. and J. Malý, , On approximate differentiability of the maximal function. Proc. Amer. Math. Soc. 138(2010), no. 1, 165–174. http://dx.doi.org/10.1090/S0002-9939-09-09971-7 CrossRefGoogle Scholar
[20] Heinonen, J. and Koskela, P., Quasiconformal maps in metric spaces with controlled geometry. Acta Math. 181(1998), no. 1, 1–61. http://dx.doi.org/10.1007/BF02392747 CrossRefGoogle Scholar
[21] Heinonen, J., Lectures on analysis on metric spaces. Universitext, Springer-Verlag, New York, 2001.Google Scholar
[22] Heinonen, J., Nonsmooth calculus. Bull. Amer. Math. Soc. (N.S.) 44(2007), no. 2, 163–232. http://dx.doi.org/10.1090/S0273-0979-07-01140-8 CrossRefGoogle Scholar
[23] Keith, S., A differentiable structure for metric measure spaces. Adv. Math. 183(2004), no. 2, 271–315. http://dx.doi.org/10.1016/S0001-8708(03)00089-6 CrossRefGoogle Scholar
[24] Keith, S., Measurable differentiable structures and the Poincaré inequality. Indiana Univ. Math. J. 53(2004), no. 4, 1127–1150. http://dx.doi.org/10.1512/iumj.2004.53.2417 CrossRefGoogle Scholar
[25] Kinnunen, J., The Hardy-Littlewood operator of a Sobolev function. Israel J. Math. 100(1997), 117–124. http://dx.doi.org/10.1007/BF02773636 CrossRefGoogle Scholar
[26] Kinnunen, J. and Latvala, V., Lebesgue points for Sobolev functions on metric spaces. Rev. Mat. Iberoamericana 18(2002), no. 3, 685–700. http://dx.doi.org/10.4171/RMI/332 CrossRefGoogle Scholar
[27] Kleiner, B.and Mackay, J., Differentiable structures on metric measure spaces: A Primer. 2011. http://arxiv:1108.1324.Google Scholar
[28] Lahti, P. and Tuominen, H., A pointwise characterization of functions of bounded variation on metric spaces. 2012. http://arxiv:1301.6897 Google Scholar
[29] Liu, F. C., Luzin type property of Sobolev functions. Indiana Univ. Math. J. 26(1977), no. 4, 645–651. http://dx.doi.org/10.1512/iumj.1977.26.26051 CrossRefGoogle Scholar
[30] Liu, F. C. and Tai, W. S., Approximate Taylor polynomials and differentiation of functions. Topol. Methods Nonlinear Anal. 3(1994), no. 1, 189–196.CrossRefGoogle Scholar
[31] Liu, F. C., Lusin properties and interpolation of Sobolev spaces. Topol. Methods Nonlinear Anal. 9(1997), no. 1, 163–177.10.12775/TMNA.1997.007CrossRefGoogle Scholar
[32] H. Luiro, On the size of the set of non-differentiability points of maximal function.2012. arxiv:1208.3971Google Scholar
[33] Luzin, N., Sur les proprié té s des fonctions mesurables. Comptes Rendus Acad. Sci. Paris 154(1912), 1688–1690.Google Scholar
[34] Malý, J., A simple proof of the Stepanov theorem on differentiability almost everywhere. Exposition. Math. 17(1999), no. 1, 59–61.Google Scholar
[35] Malý, J. and L. Zajíček, , Approximate differentiation: Jarn´ık points. Fund. Math. 140(1991), no. 1, 87–97.CrossRefGoogle Scholar
[36] Miranda, M. Jr., Functions of bounded variation on “good” metric spaces. J. Math. Pures Appl. (9) 82(2003), no. 8, 975–1004.CrossRefGoogle Scholar
[37] Ranjbar-Motlagh, A., Generalized Stepanov type theorem with applications over metric-measure spaces. Houston J. Math. 34(2008), no. 2, 623–635.Google Scholar
[38] Semmes, S., Some novel types of fractal geometry. Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York, 2001.Google Scholar
[39] Shanmugalingam, N., Newtonian spaces: an extension of Sobolev spaces to metric spaces. Rev. Mat. Iberoamericana 16(2000), no. 2, 243–279. http://dx.doi.org/10.4171/RMI/275 CrossRefGoogle Scholar
[40] Stepanoff, W., Sur les conditions de l’existence de la différentielle totale. Rec. Math. Soc. Math. Moscou 32(1925), no. 3, 511–526.Google Scholar
[41] Whitney, H., On totally differentiable and smooth functions. Pacific J. Math. 1(1951), 143–159. http://dx.doi.org/10.2140/pjm.1951.1.143 CrossRefGoogle Scholar