Let H0m(Ω) denote the so-called Sobolev space consisting of functions denned on a region Ω in n-dimensional Euclidean space, which together with their generalized derivatives of all orders ⩽m belong to 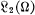, and which vanish in a certain sense on the boundary ∂Ω. (Precise definitions are given in the next section.) For each pair m, k of non-negative integers the inclusion H0m+k(Ω) ⊂ H0m(Ω) defines a natural “embedding” map. For the case of a bounded region Ω it is well known that these maps are completely continuous, and even, for sufficiently large k, of Hilbert-Schmidt type. We have discussed complete continuity in the case of unbounded regions in an earlier paper; here we consider conditions on Ω which imply the Hilbert-Schmidt property for embeddings.