No CrossRef data available.
Published online by Cambridge University Press: 15 December 2022
Tree trace reconstruction aims to learn the binary node labels of a tree, given independent samples of the tree passed through an appropriately defined deletion channel. In recent work, Davies, Rácz, and Rashtchian [10] used combinatorial methods to show that
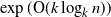 $\exp({\mathrm{O}} (k \log_{k} n))$
samples suffice to reconstruct a complete k-ary tree with n nodes with high probability. We provide an alternative proof of this result, which allows us to generalize it to a broader class of tree topologies and deletion models. In our proofs we introduce the notion of a subtrace, which enables us to connect with and generalize recent mean-based complex analytic algorithms for string trace reconstruction.
$\exp({\mathrm{O}} (k \log_{k} n))$
samples suffice to reconstruct a complete k-ary tree with n nodes with high probability. We provide an alternative proof of this result, which allows us to generalize it to a broader class of tree topologies and deletion models. In our proofs we introduce the notion of a subtrace, which enables us to connect with and generalize recent mean-based complex analytic algorithms for string trace reconstruction.