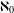1 results
CARDINALITY OF INVERSE LIMITS WITH UPPER SEMICONTINUOUS BONDING FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 23 September 2014, pp. 167-174
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
-
We explore the cardinality of generalised inverse limits. Among other things, we show that, for any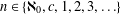
$n\in \{ℵ_{0},c,1,2,3,\dots \}$, there is an upper semicontinuous function with the inverse limit having exactly 
$n$ points. We also prove that if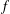 
$f$ is an upper semicontinuous function whose graph is a continuum, then the cardinality of the corresponding inverse limit is either 1, 
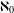$ℵ_{0}$ or 
$c$. This generalises the recent result of I. Banič and J. Kennedy, which claims that the same is true in the case where the graph is an arc.
