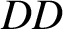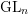Many bundle gerbes are either infinite-dimensional, or finite-dimensional but built using submersions that are far from being fibre bundles. Murray and Stevenson [‘A note on bundle gerbes and infinite-dimensionality’, J. Aust. Math. Soc.90(1) (2011), 81–92] proved that gerbes on simply-connected manifolds, built from finite-dimensional fibre bundles with connected fibres, always have a torsion 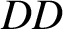$DD$ -class. I prove an analogous result for a wide class of gerbes built from principal bundles, relaxing the requirements on the fundamental group of the base and the connected components of the fibre, allowing both to be nontrivial. This has consequences for possible models for basic gerbes, the classification of crossed modules of finite-dimensional Lie groups, the coefficient Lie-2-algebras for higher gauge theory on principal 2-bundles and finite-dimensional twists of topological K-theory.

We compute the image of any choice of complex conjugation on the Galois representations associated to regular algebraic cuspidal automorphic representations and to torsion classes in the cohomology of locally symmetric spaces for $\text{GL}_{n}$ over a totally real field $F$.