Let X be a 4-dimensional toric orbifold. If 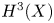 $H^{3}(X)$ has a non-trivial odd primary torsion, then we show that X is homotopy equivalent to the wedge of a Moore space and a CW-complex. As a corollary, given two 4-dimensional toric orbifolds having no 2-torsion in the cohomology, we prove that they have the same homotopy type if and only their integral cohomology rings are isomorphic.
$H^{3}(X)$ has a non-trivial odd primary torsion, then we show that X is homotopy equivalent to the wedge of a Moore space and a CW-complex. As a corollary, given two 4-dimensional toric orbifolds having no 2-torsion in the cohomology, we prove that they have the same homotopy type if and only their integral cohomology rings are isomorphic.