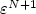Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (0)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

thin conducting sheets

ESAIM: Mathematical Modelling and Numerical Analysis (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

High order transmission conditions for thin conductive sheets in magneto-quasistatics
Kersten Schmidt, Sébastien Tordeux
Journal:

ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 6 / November 2011

Published online by Cambridge University Press:

28 June 2011, pp. 1115-1140

Print publication:

November 2011
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
We propose transmission conditions of order 1, 2 and 3 approximating the shielding behaviour of thin conducting curved sheets for the magneto-quasistatic eddy current model in 2D. This model reduction applies to sheets whose thicknesses ε are at the order of the skin depth or essentially smaller. The sheet has itself not to be resolved, only its midline is represented by an interface. The computation is directly in one step with almost no additional cost. We prove the well-posedness w.r.t. to the small parameter ε and obtain optimal bound for the modelling error outside the sheet of order $\varepsilon^{N+1}$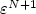 for the condition of order N. We end the paper with numerical experiments involving high order finite elements for sheets with varying curvature.