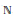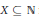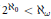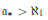1 results
MAD Saturated Families and SANE Player
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 6 / 01 December 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1416-1435
- Print publication:
- 01 December 2011
-
- Article
-
- You have access
- Export citation
-
We throw some light on the question: is there a MAD family (a maximal family of infinite subsets of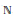
$\mathbb{N}$, the intersection of any two is finite) that is saturated (=completely separable i.e., any 
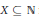$X\,\subseteq \,\mathbb{N}$ is included in a finite union of members of the family or includes a member (and even continuum many members) of the family). We prove that it is hard to prove the consistency of the negation:(i) if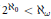
${{2}^{{{\aleph }_{0}}}}\,<\,{{\aleph }_{\omega }}$, then there is such a family;(ii) if there is no such family, then some situation related to pcf holds whose consistency is large (and if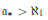
${{a}_{*}}\,>\,{{\aleph }_{1}}$ even unknown);(iii) if, e.g., there is no inner model with measurables, then there is such a family.
