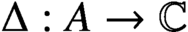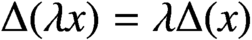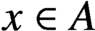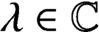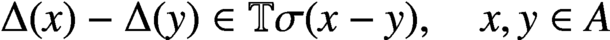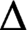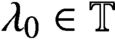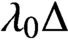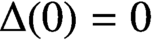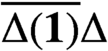Li et al. [‘Weak 2-local isometries on uniform algebras and Lipschitz algebras’, Publ. Mat.63 (2019), 241–264] generalized the Kowalski–Słodkowski theorem by establishing the following spherical variant: let A be a unital complex Banach algebra and let 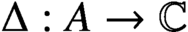$\Delta : A \to \mathbb {C}$ be a mapping satisfying the following properties:

1. (a) 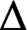$\Delta $ is 1-homogeneous (that is, 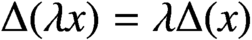$\Delta (\lambda x)=\lambda \Delta (x)$ for all 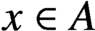$x \in A$ , 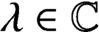$\lambda \in \mathbb C$ );

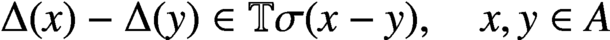2. (b) $\Delta (x)-\Delta (y) \in \mathbb {T}\sigma (x-y), \quad x,y \in A$ .

Then 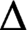$\Delta $ is linear and there exists 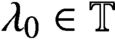$\lambda _{0} \in \mathbb {T}$ such that 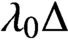$\lambda _{0}\Delta $ is multiplicative. In this note we prove that if (a) is relaxed to 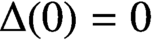$\Delta (0)=0$ , then 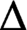$\Delta $ is complex-linear or conjugate-linear and 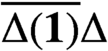$\overline {\Delta (\mathbf {1})}\Delta $ is multiplicative. We extend the Kowalski–Słodkowski theorem as a conclusion. As a corollary, we prove that every 2-local map in the set of all surjective isometries (without assuming linearity) on a certain function space is in fact a surjective isometry. This gives an affirmative answer to a problem on 2-local isometries posed by Molnár [‘On 2-local *-automorphisms and 2-local isometries of B(H)', J. Math. Anal. Appl.479(1) (2019), 569–580] and also in a private communication between Molnár and O. Hatori, 2018.