We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Consider a map of class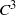 
${C}^{3} $ with nonflat critical points and with all periodic points hyperbolic repelling. We show that the ‘backward contracting condition’ implies the summability condition. This result is the converse of Theorem 3 of Bruin et al. [‘Large derivatives, backward contraction and invariant densities for interval maps’, Invent. Math. 172 (2008), 509–533].
