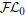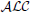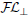The inexpressive Description Logic (DL) 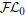 ${\cal F}{{\cal L}_0}$
, which has conjunction and value restriction as its only concept constructors, had fallen into disrepute when it turned out that reasoning in
${\cal F}{{\cal L}_0}$
, which has conjunction and value restriction as its only concept constructors, had fallen into disrepute when it turned out that reasoning in 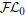 ${\cal F}{{\cal L}_0}$
w.r.t. general TBoxes is ExpTime-complete, that is, as hard as in the considerably more expressive logic
${\cal F}{{\cal L}_0}$
w.r.t. general TBoxes is ExpTime-complete, that is, as hard as in the considerably more expressive logic 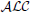 ${\cal A}{\cal L}{\cal C}$
. In this paper, we rehabilitate
${\cal A}{\cal L}{\cal C}$
. In this paper, we rehabilitate 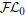 ${\cal F}{{\cal L}_0}$
by presenting a dedicated subsumption algorithm for
${\cal F}{{\cal L}_0}$
by presenting a dedicated subsumption algorithm for 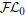 ${\cal F}{{\cal L}_0}$
, which is much simpler than the tableau-based algorithms employed by highly optimized DL reasoners. Our experiments show that the performance of our novel algorithm, as prototypically implemented in our
${\cal F}{{\cal L}_0}$
, which is much simpler than the tableau-based algorithms employed by highly optimized DL reasoners. Our experiments show that the performance of our novel algorithm, as prototypically implemented in our 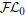 ${\cal F}{{\cal L}_0}$
wer reasoner, compares very well with that of the highly optimized reasoners.
${\cal F}{{\cal L}_0}$
wer reasoner, compares very well with that of the highly optimized reasoners. 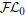 ${\cal F}{{\cal L}_0}$
wer can also deal with ontologies written in the extension
${\cal F}{{\cal L}_0}$
wer can also deal with ontologies written in the extension 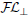 ${\cal F}{{\cal L}_ \bot }$
of
${\cal F}{{\cal L}_ \bot }$
of 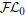 ${\cal F}{{\cal L}_0}$
with the top and the bottom concept by employing a polynomial-time reduction, shown in this paper, which eliminates top and bottom. We also investigate the complexity of reasoning in DLs related to the Horn-fragments of
${\cal F}{{\cal L}_0}$
with the top and the bottom concept by employing a polynomial-time reduction, shown in this paper, which eliminates top and bottom. We also investigate the complexity of reasoning in DLs related to the Horn-fragments of 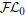 ${\cal F}{{\cal L}_0}$
and
${\cal F}{{\cal L}_0}$
and 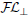 ${\cal F}{{\cal L}_ \bot }$
.
${\cal F}{{\cal L}_ \bot }$
.
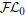 ${\cal F}{{\cal L}_0}$
wer Reasoner
${\cal F}{{\cal L}_0}$
wer Reasoner