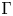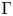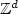We study the $\Gamma$-convergence of nonconvex vectorial integral functionals whose integrands satisfy possibly degenerate growth and coercivity conditions. The latter involve suitable scale-dependent weight functions. We prove that under appropriate uniform integrability conditions on the weight functions, which shall belong to a Muckenhoupt class, the corresponding functionals $\Gamma$-converge, up to subsequences, to a degenerate integral functional defined on a limit weighted Sobolev space. The general analysis is then applied to the case of random stationary integrands and weights to prove a stochastic homogenization result for the corresponding functionals.

We consider the variant of stochastic homogenization theory introduced in [X. Blanc, C.Le Bris and P.-L. Lions, C. R. Acad. Sci. Série I 343 (2006)717–724.; X. Blanc, C. Le Bris and P.-L. Lions, J. Math. Pures Appl.88 (2007) 34–63.]. The equation under consideration is a standardlinear elliptic equation in divergence form, where the highly oscillatory coefficient isthe composition of a periodic matrix with a stochastic diffeomorphism. The homogenizedlimit of this problem has been identified in [X. Blanc, C. Le Bris and P.-L. Lions,C. R. Acad. Sci. Série I 343 (2006) 717–724.]. We firstestablish, in the one-dimensional case, a convergence result (with an explicit rate) onthe residual process, defined as the difference between the solution to the highlyoscillatory problem and the solution to the homogenized problem. We next return to themultidimensional situation. As often in random homogenization, the homogenized matrix isdefined from a so-called corrector function, which is the solution to a problem set on theentire space. We describe and prove the almost sure convergence of an approximationstrategy based on truncated versions of the corrector problem.

We establish an optimal, linear rate of convergence for the stochastic homogenization of discrete linear elliptic equations. We consider the model problem of independent and identically distributed coefficients on a discretized unit torus. We show that the difference between the solution to the random problem on the discretized torus and the first two terms of the two-scale asymptotic expansion has the same scaling as in the periodic case. In particular the L2-norm in probability of the H1-norm in space of this error scales like ε, where ε is the discretization parameter of the unit torus. The proof makes extensive use of previous results by the authors, and of recent annealed estimates on the Green’s function by Marahrens and the third author.

We introduce and analyze a numerical strategy to approximate effective coefficients in stochastic homogenization of discrete ellipticequations. In particular, we consider the simplest case possible: An elliptic equation on the d-dimensional lattice $\mathbb{Z}^d$with independent and identically distributed conductivities on the associated edges.Recent results by Otto and the author quantify the error made by approximatingthe homogenized coefficient by the averaged energy of a regularizedcorrector (with parameter T) on some box of finite size L. In this article, we replace the regularizedcorrector (which is the solution of a problem posed on $\mathbb{Z}^d$) by some practically computable proxy on some box of size R ≥ L, and quantify the associated additional error.In order to improve the convergence, one may also consider N independentrealizations of the computable proxy, and take the empirical average of the associated approximate homogenized coefficients.A natural optimization problem consists in properly choosing T, R, L and N in order toreduce the error at given computational complexity.Our analysis is sharp and sheds some light on this question.In particular, we propose and analyze a numerical algorithm to approximate the homogenized coefficients, taking advantage of the (nearly) optimal scalings of the errorswe derive. The efficiency of the approach is illustrated by a numerical study in dimension 2.