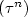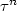Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

2 results

  • Stability of solutions of BSDEs with random terminal time

  • Sandrine Toldo
  • Journal:
    ESAIM: Probability and Statistics / Volume 10 / February 2006
    Published online by Cambridge University Press:
    09 March 2006, pp. 141-163
    Print publication:
    February 2006

  • In this paper, we study the stability of the solutions of Backward Stochastic Differential Equations (BSDE for short) with an almost surelyfinite random terminal time. More precisely, we are going to show that if (Wn ) is a sequence of scaled random walks or a sequence of martingales that converges to a Brownian motion W and if $(\tau^n)$ 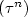is a sequence of stopping times that converges to a stopping time τ, then the solution of the BSDE driven by Wn with random terminal time $\tau^n$ 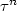converges to the solution of the BSDE driven by W with random terminal time τ.