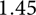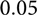We perform statistical analyses on spatiotemporal patterns in the magnitude distribution of induced earthquakes in the Groningen natural gas field. The seismic catalogue contains 336 earthquakes with (local) magnitudes above 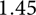$1.45$ , observed in the period between 1 January 1995 and 1 January 2022. 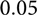An exploratory moving-window analysis of maximum-likelihood b-values in both time and space does not reveal any significant variation in time, but does reveal a spatial variation that exceeds the $0.05$ significance level.

In search for improved understanding of the observed spatial variations in physical terms we test five physical reservoir properties as possible b-value predictors. The predictors include two static (spatial, time-independent) properties: the reservoir layer thickness, and the topographic gradient (a measure of the degree of faulting intensity in the reservoir); and three dynamic (spatiotemporal, time-dependent) properties: the pressure drop due to gas extraction, the resulting reservoir compaction, and a measure for the resulting induced stress. The latter property is the one that is currently used in the seismic source models that feed into the state-of-the-art hazard and risk assessment.

We assess the predictive capabilities of the five properties by statistical evaluation of both moving window analysis, and maximum-likelihood parameter estimation for a number of simple functional forms that express the b-value as a function of the predictor. We find significant linear trends of the b-value for both topographic gradient and induced stress, but even more pronouncedly for reservoir thickness. Also for the moving window analysis and the step function fit, the reservoir thickness provides the most significant results.

We conclude that reservoir thickness is a strong predictor for spatial b-value variations in the Groningen field. We propose to develop a forecasting model for Groningen magnitude distributions conditioned on reservoir thickness, to be used alongside, or as a replacement, for the current models conditioned on induced stress.