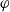This paper concerns arithmetic families of $\varphi $-modules over reduced affinoid spaces. For such a family, we first prove that the slope polygons are lower semicontinuous around any rigid point. We further prove that if the slope polygons are locally constant around a rigid point, then around this point, the family has a global slope filtration after base change to some extended Robba ring.

Over a perfect field $k$ of characteristic $p > 0$, we construct a ‘Witt vector cohomology with compact supports’ for separated $k$-schemes of finite type, extending (after tensorization with ${\mathbb Q}$) the classical theory for proper $k$-schemes. We define a canonical morphism from rigid cohomology with compact supports to Witt vector cohomology with compact supports, and we prove that it provides an identification between the latter and the slope ${<}1$ part of the former. Over a finite field, this allows one to compute congruences for the number of rational points in special examples. In particular, the congruence modulo the cardinality of the finite field of the number of rational points of a theta divisor on an abelian variety does not depend on the choice of the theta divisor. This answers positively a question by J.-P. Serre.