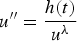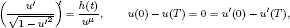2 results
Periodic solutions for a second-order differential equation with indefinite weak singularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1135-1152
- Print publication:
- October 2019
-
- Article
- Export citation
-
As a consequence of the main result of this paper efficient conditions guaranteeing the existence of a T −periodic solution to the second-order differential equation
are established. Here, h ∈ L(ℝ/Tℤ) is a piecewise-constant sign-changing function and the non-linear term presents a weak singularity at 0 (i.e. λ ∈ (0, 1)).
$${u}^{\prime \prime} = \displaystyle{{h(t)} \over {u^\lambda }}$$
Periodic solutions for indefinite singular perturbations of the relativistic acceleration
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 703-712
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
-
Using the Leray–Schauder degree, we study the existence of solutions for the following periodic differential equation with relativistic acceleration and singular nonlinearity:
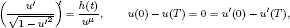
where μ > 1 and the weight h: [0, T] → ℝ is a continuous sign-changing function. There are no a priori estimates on the set of positive solutions (a condition used in general to apply the Leray–Schauder degree), and we prove that no solution of the equation appears on the boundary of an unbounded open set during the deformation to an autonomous problem.
