We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we show that Leavitt path algebras of weighted graphs and Leavitt path algebras of separated graphs are intimately related. We prove that any Leavitt path algebra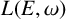 
$L(E,\omega )$ of a row-finite vertex weighted graph 
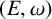$(E,\omega )$ is 
$*$-isomorphic to the lower Leavitt path algebra of a certain bipartite separated graph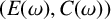 
$(E(\omega ),C(\omega ))$. For a general locally finite weighted graph 
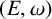$(E, \omega )$, we show that a certain quotient 
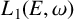$L_1(E,\omega )$ of 
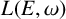$L(E,\omega )$ is 
$*$-isomorphic to an upper Leavitt path algebra of another bipartite separated graph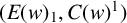 
$(E(w)_1,C(w)^1)$. We furthermore introduce the algebra 
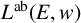${L^{\mathrm {ab}}} (E,w)$, which is a universal tame 
$*$-algebra generated by a set of partial isometries. We draw some consequences of our results for the structure of ideals of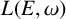 
$L(E,\omega )$, and we study in detail two different maximal ideals of the Leavitt algebra 
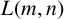$L(m,n)$.
