We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that, assuming the Axiom of Determinacy, every non-selfdual Wadge class can be constructed by starting with those of level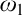 
$\omega _1$
(that is, the ones that are closed under Borel preimages) and iteratively applying the operations of expansion and separated differences. The proof is essentially due to Louveau, and it yields at the same time a new proof of a theorem of Van Wesep (namely, that every non-selfdual Wadge class can be expressed as the result of a Hausdorff operation applied to the open sets). The exposition is self-contained, except for facts from classical descriptive set theory.
