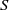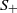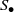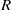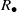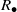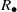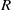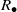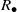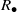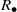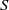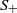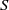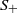A semiring is a set 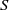$S$ with two binary operations $+ $ and $\cdot $ such that both the additive reduct 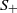${S}_{+ } $ and the multiplicative reduct 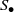${S}_{\bullet } $ are semigroups which satisfy the distributive laws. If 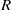$R$ is a ring, then, following Chaptal [‘Anneaux dont le demi-groupe multiplicatif est inverse’, C. R. Acad. Sci. Paris Ser. A–B 262 (1966), 274–277], 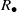${R}_{\bullet } $ is a union of groups if and only if 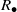${R}_{\bullet } $ is an inverse semigroup if and only if 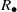${R}_{\bullet } $ is a Clifford semigroup. In Zeleznikow [‘Regular semirings’, Semigroup Forum 23 (1981), 119–136], it is proved that if 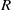$R$ is a regular ring then 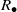${R}_{\bullet } $ is orthodox if and only if 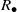${R}_{\bullet } $ is a union of groups if and only if 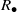${R}_{\bullet } $ is an inverse semigroup if and only if 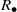${R}_{\bullet } $ is a Clifford semigroup. The latter result, also known as Zeleznikow’s theorem, does not hold in general even for semirings 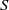$S$ with 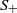${S}_{+ } $ a semilattice Zeleznikow [‘Regular semirings’, Semigroup Forum 23 (1981), 119–136]. The Zeleznikow problem on a certain class of semirings involves finding condition(s) such that Zeleznikow’s theorem holds on that class. The main objective of this paper is to solve the Zeleznikow problem for those semirings 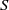$S$ for which 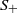${S}_{+ } $ is a semilattice.