Search

Propositional quantifiers are quantifiers binding proposition letters, understood as variables. This Element introduces propositional quantifiers and explains why they are especially interesting in the context of propositional modal logics. It surveys the main results on propositionally quantified modal logics which have been obtained in the literature, presents a number of open questions, and provides examples of applications of such logics to philosophical problems.

Propositional modal logic over relational frames is naturally extended with propositional quantifiers by letting them range over arbitrary sets of worlds of the relevant frame. This is also known as second-order propositional modal logic. The propositionally quantified modal logic of a class of relational frames is often not axiomatizable, although there are known exceptions, most notably the case of frames validating the strong modal logic 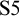$\mathrm {S5}$. Here, we develop new general methods with which many of the open questions in this area can be answered. We illustrate the usefulness of these methods by applying them to a range of examples, which provide a detailed picture of which normal modal logics define classes of relational frames whose propositionally quantified modal logic is axiomatizable. We also apply these methods to establish new results in the multimodal case.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

Propositional Quantifiers

AXIOMATIZABILITY OF PROPOSITIONALLY QUANTIFIED MODAL LOGICS ON RELATIONAL FRAMES

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

Propositional Quantifiers

AXIOMATIZABILITY OF PROPOSITIONALLY QUANTIFIED MODAL LOGICS ON RELATIONAL FRAMES