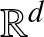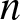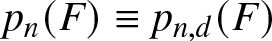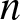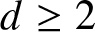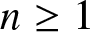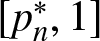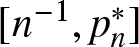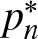Given a sequence of independent random vectors taking values in 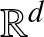${\mathbb R}^d$ and having common continuous distribution function F, say that the 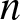$n^{\rm \scriptsize}$th observation sets a (Pareto) record if it is not dominated (in every coordinate) by any preceding observation. Let 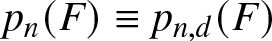$p_n(F) \equiv p_{n, d}(F)$ denote the probability that the 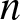$n^{\rm \scriptsize}$th observation sets a record. There are many interesting questions to address concerning pn and multivariate records more generally, but this short paper focuses on how pn varies with F, particularly if, under F, the coordinates exhibit negative dependence or positive dependence (rather than independence, a more-studied case). We introduce new notions of negative and positive dependence ideally suited for such a study, called negative record-setting probability dependence (NRPD) and positive record-setting probability dependence (PRPD), relate these notions to existing notions of dependence, and for fixed 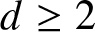$d \geq 2$ and 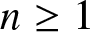$n \geq 1$ prove that the image of the mapping pn on the domain of NRPD (respectively, PRPD) distributions is 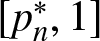$[p^*_n, 1]$ (resp., 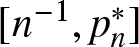$[n^{-1}, p^*_n]$), where 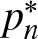$p^*_n$ is the record-setting probability for any continuous F governing independent coordinates.

We discuss some properties of a class of multivariate mixed Erlang distributions with different scale parameters and describes various distributional properties related to applications in insurance risk theory. Some representations involving scale mixtures, generalized Esscher transformations, higher-order equilibrium distributions, and residual lifetime distributions are derived. These results allows for the study of stop-loss moments, premium calculation, and the risk allocation problem. Finally, some results concerning minimum and maximum variables are derived and applied to pricing joint life and last survivor policies.

In a series of recent papers, Heyde (1975), Heyde and Leslie (1976), Hall (1979) and Brown (1980) obtained upper bounds on the uniform distance of a scale mixture from its parent distribution. Using a different technique we obtain further bounds which are more meaningful and superior in some applications. The new technique is then applied to obtain bounds on the uniform distance of a location mixture from its parent distribution. Comparison of the new bounds and the earlier ones is given.