We generalize Löwner's method for proving that matrix monotone functions are operator monotone. The relation 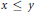$x\,\le \,y$ on bounded operators is our model for a definition of 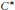${{C}^{*}}$-relations being residually finite dimensional.

Our main result is a meta-theorem about theorems involving relations on bounded operators. If we can show there are residually finite dimensional relations involved and verify a technical condition, then such a theorem will follow from its restriction to matrices.

Applications are shown regarding norms of exponentials, the norms of commutators, and “positive” noncommutative $*$-polynomials.

We investigate a class of triangular UHF algebras which have the special property that there exists a sequence of unital multiplicative contractive finite-rank conditional expectations of the algebra into itself, which converges strongly to the identity, whose ranges form an increasing chain with dense union. A partial classification is given in terms of a local finiteness property, and a delimiting counterexample is obtained. Associated inverse limit algebras are considered, and a characterization of residually finite dimensional triangular AF algebras is obtained.

1991 Mathematics Subject Classification: 47D25, 46J35.