The paper studies modular reduction techniques for abstract regular and chiral polytopes, with two purposes in mind: first, to survey the literature about modular reduction in polytopes; and second, to apply modular reduction, with moduli given by primes in 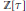 $\mathbb{Z}\left[ \tau \right]$ (with
$\mathbb{Z}\left[ \tau \right]$ (with  $\tau$ the golden ratio), to construct new regular 4-polytopes of hyperbolic types
$\tau$ the golden ratio), to construct new regular 4-polytopes of hyperbolic types 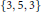 $\{3,\,5,\,3\}$ and
$\{3,\,5,\,3\}$ and 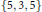 $\{5,\,3,\,5\}$ with automorphism groups given by finite orthogonal groups.
$\{5,\,3,\,5\}$ with automorphism groups given by finite orthogonal groups.