1 results
Axiomatizing Kripke's theory of truth
-
- Journal:
- The Journal of Symbolic Logic / Volume 71 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 12 March 2014, pp. 677-712
- Print publication:
- June 2006
-
- Article
- Export citation
-
We investigate axiomatizations of Kripke's theory of truth based on the Strong Kleene evaluation scheme for treating sentences lacking a truth value. Feferman's axiomatization KF formulated in classical logic is an indirect approach, because it is not sound with respect to Kripke's semantics in the straightforward sense: only the sentences that can be proved to be true in KF are valid in Kripke's partial models. Reinhardt proposed to focus just on the sentences that can be proved to be true in KF and conjectured that the detour through classical logic in KF is dispensable. We refute Reinhardt's Conjecture, and provide a direct axiomatization PKF of Kripke's theory in partial logic. We argue that any natural axiomatization of Kripke's theory in Strong Kleene logic has the same proof-theoretic strength as PKF. namely the strength of the system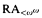
ramified analysis or a system of Tarskian ramified truth up to ωω. Thus any such axiomatization is much weaker than Feferman's axiomatization KF in classical logic, which is equivalent to the system 
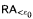of ramified analysis up to ε0.
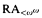ramified analysis or a system of Tarskian ramified truth up to ω
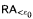of ramified analysis up to ε