This article discusses the concept of rational equivalence in tropical geometry (and replaces an older, imperfect version). We give the basic definitions in the context of tropical varieties without boundary points and prove some basic properties. We then compute the “bounded” Chow groups of
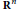 ${{\mathbf{R}}^{n}}$
by showing that they are isomorphic to the group of fan cycles. The main step in the proof is of independent interest. We show that every tropical cycle in
${{\mathbf{R}}^{n}}$
by showing that they are isomorphic to the group of fan cycles. The main step in the proof is of independent interest. We show that every tropical cycle in
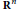 ${{\mathbf{R}}^{n}}$
is a sum of (translated) fan cycles. This also proves that the intersection ring of tropical cycles is generated in codimension 1 (by hypersurfaces).
${{\mathbf{R}}^{n}}$
is a sum of (translated) fan cycles. This also proves that the intersection ring of tropical cycles is generated in codimension 1 (by hypersurfaces).