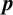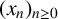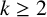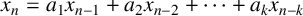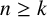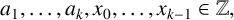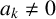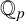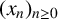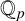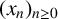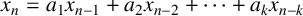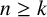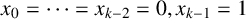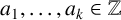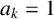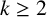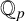1 results
$\boldsymbol {p}$-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 19-28
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Let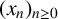
$(x_n)_{n\geq 0}$ be a linear recurrence of order 
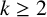$k\geq 2$ satisfying 
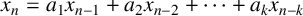$x_n=a_1x_{n-1}+a_2x_{n-2}+\cdots +a_kx_{n-k}$ for all integers 
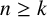$n\geq k$, where 
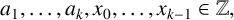$a_1,\ldots ,a_k,x_0,\ldots , x_{k-1}\in \mathbb {Z},$ with 
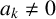$a_k\neq 0$. Sanna [‘The quotient set of k-generalised Fibonacci numbers is dense in 
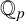$\mathbb {Q}_p$’, Bull. Aust. Math. Soc. 96(1) (2017), 24–29] posed the question of classifying primes p for which the quotient set of 
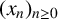$(x_n)_{n\geq 0}$ is dense in 
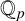$\mathbb {Q}_p$. We find a sufficient condition for denseness of the quotient set of the kth-order linear recurrence 
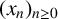$(x_n)_{n\geq 0}$ satisfying 
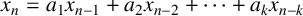$ x_{n}=a_1x_{n-1}+a_2x_{n-2}+\cdots +a_kx_{n-k}$ for all integers 
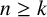$n\geq k$ with initial values 
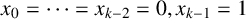$x_0=\cdots =x_{k-2}=0,x_{k-1}=1$, where 
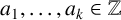$a_1,\ldots ,a_k\in \mathbb {Z}$ and 
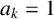$a_k=1$. We show that, given a prime p, there are infinitely many recurrence sequences of order 
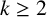$k\geq 2$ whose quotient sets are not dense in 
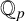$\mathbb {Q}_p$. We also study the quotient sets of linear recurrence sequences with coefficients in certain arithmetic and geometric progressions.
