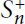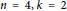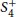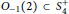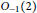Motivated by a question of A. Skalski and P. M. Sołtan (2016) about inner faithfulness of S. Curran’s map of extending a quantum increasing sequence to a quantum permutation, we revisit the results and techniques of T. Banica and J. Bichon (2009) and study some group-theoretic properties of the quantum permutation group on points. This enables us not only to answer the aforementioned question in the positive for the case where 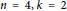 $n\,=\,4,\,k\,=\,2$, but also to classify the automorphisms of
$n\,=\,4,\,k\,=\,2$, but also to classify the automorphisms of 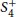 $S_{4}^{+}$, describe all the embeddings
$S_{4}^{+}$, describe all the embeddings 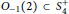 ${{O}_{-1}}(2)\,\subset \,S_{4}^{+}$ and show that all the copies of
${{O}_{-1}}(2)\,\subset \,S_{4}^{+}$ and show that all the copies of 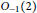 ${{O}_{-1}}(2)$ inside
${{O}_{-1}}(2)$ inside 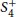 $S_{4}^{+}$are conjugate. We then use these results to show that the converse to the criterion we applied to answer the aforementioned question is not valid.
$S_{4}^{+}$are conjugate. We then use these results to show that the converse to the criterion we applied to answer the aforementioned question is not valid.
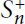 $S_{n}^{+}$
$S_{n}^{+}$