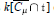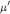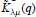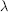We study the coordinate rings of 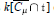$k\left[ \overline{{{\text{C}}_{\mu }}}\,\bigcap \,\text{t} \right]$ scheme-theoretic intersections of nilpotent orbit closures with the diagonal matrices. Here 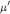${\mu }'$ gives the Jordan block structure of the nilpotent matrix. de Concini and Procesi [5] proved a conjecture of Kraft [12] that these rings are isomorphic to the cohomology rings of the varieties constructed by Springer [22, 23]. 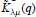The famous $q$-Kostka polynomial ${{\tilde{K}}_{\lambda \mu }}(q)$ is the Hilbert series for the multiplicity of the irreducible symmetric group representation indexed by 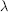$\lambda $ in the ring 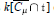$k\left[ \overline{{{\text{C}}_{\mu }}}\,\bigcap \,\text{t} \right]$. Lascoux and Schützenberger [15, 13] gave combinatorially a decomposition of 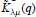${{\tilde{K}}_{\lambda \mu }}(q)$ as a sum of “atomic” polynomials with non-negative integer coefficients, and Lascoux proposed a corresponding decomposition in the cohomology model.

Our work provides a geometric interpretation of the atomic decomposition. The Frobenius-splitting results of Mehta and van der Kallen [19] imply a direct-sum decomposition of the ideals of nilpotent orbit closures, arising from the inclusions of the corresponding sets. We carry out the restriction to the diagonal using a recent theorem of Broer [3]. This gives a direct-sum decomposition of the ideals yielding the 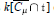$k\left[ \overline{{{\text{C}}_{\mu }}}\,\bigcap \,\text{t} \right]$, and a new proof of the atomic decomposition of the $q$-Kostka polynomials.