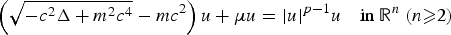1 results
On critical and supercritical pseudo-relativistic nonlinear Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1241-1263
- Print publication:
- June 2020
-
- Article
- Export citation
-
In this paper, we investigate existence and non-existence of a nontrivial solution to the pseudo-relativistic nonlinear Schrödinger equation
involving an H1/2-critical/supercritical power-type nonlinearity, that is, p ⩾ ((n + 1)/(n − 1)). We prove that in the non-relativistic regime, there exists a nontrivial solution provided that the nonlinearity is H1/2-critical/supercritical but it is H1-subcritical. On the other hand, we also show that there is no nontrivial bounded solution either (i) if the nonlinearity is H1/2-critical/supercritical in the ultra-relativistic regime or (ii) if the nonlinearity is H1-critical/supercritical in all cases.
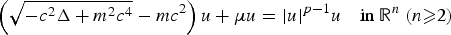$$\left( \sqrt{-c^2\Delta + m^2 c^4}-mc^2\right) u + \mu u = \vert u \vert^{p-1}u\quad {\rm in}~{\open R}^n~(n \ges 2) $$
