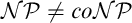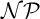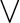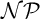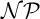Search

Cook and Reckhow [5] pointed out that 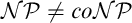$\mathcal {N}\mathcal {P} \neq co\mathcal {N}\mathcal {P}$ iff there is no propositional proof system that admits polynomial size proofs of all tautologies. The theory of proof complexity generators aims at constructing sets of tautologies hard for strong and possibly for all proof systems. We focus on a conjecture from [16] in foundations of the theory that there is a proof complexity generator hard for all proof systems. This can be equivalently formulated (for p-time generators) without a reference to proof complexity notions as follows:

• There exists a p-time function g stretching each input by one bit such that its range $rng(g)$ intersects all infinite $\mathcal {N}\mathcal {P}$ sets.

We consider several facets of this conjecture, including its links to bounded arithmetic (witnessing and independence results), to time-bounded Kolmogorov complexity, to feasible disjunction property of propositional proof systems and to complexity of proof search. We argue that a specific gadget generator from [18] is a good candidate for g. We define a new hardness property of generators, the

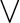$\bigvee $-hardness, and show that one specific gadget generator is the

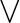$\bigvee $-hardest (w.r.t. any sufficiently strong proof system). We define the class of feasibly infinite

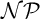$\mathcal {N}\mathcal {P}$ sets and show, assuming a hypothesis from circuit complexity, that the conjecture holds for all feasibly infinite

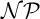$\mathcal {N}\mathcal {P}$ sets.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

ON THE EXISTENCE OF STRONG PROOF COMPLEXITY GENERATORS

19 - Hard Tautologies

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

ON THE EXISTENCE OF STRONG PROOF COMPLEXITY GENERATORS

19 - Hard Tautologies