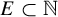1 results
Direct and inverse results for popular differences in trees of positive dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 481-508
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We establish analogues for trees of results relating the density of a set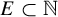
${E \subset \mathbb {N}}$, the density of its set of popular differences and the structure of E. To obtain our results, we formalize a correspondence principle of Furstenberg and Weiss which relates combinatorial data on a tree to the dynamics of a Markov process. Our main tools are Kneser-type inverse theorems for sets of return times in measure-preserving systems. In the ergodic setting, we use a recent result of the first author with Björklund and Shkredov and a stability-type extension (proved jointly with Shkredov); we also prove a new result for non-ergodic systems.
