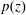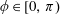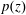1 results
Sector Analogue of the Gauss–Lucas Theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 318-338
- Print publication:
- April 2021
-
- Article
- Export citation
-
The classical Gauss–Lucas theorem states that the critical points of a polynomial with complex coefficients are in the convex hull of its zeros. This fundamental theorem follows from the fact that if all the zeros of a polynomial are in a half plane, then the same is true for its critical points. The main result of this work replaces the half plane with a sector as follows.
We show that if the coefficients of a monic polynomial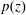
$p(z)$ are in the sector {tei𝜓 : 𝜓∈ [0, 𝜙], t⩾0}, for some 
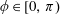$\unicode[STIX]{x1D719}\in [0,\unicode[STIX]{x1D70B})$, and the zeros are not in its interior, then the critical points of 
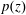$p(z)$ are also not in the interior of that sector.In addition, we give a necessary condition for a polynomial to satisfy the premise of the main result.
