We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let C be a bounded, closed, convex subset of a uniformly convex Banach space X. We investigate the existence of common fixed points for pointwise Lipschitzian semigroups of nonlinear mappings Tt:C→C, where each Tt is pointwise Lipschitzian. The latter means that there exists a family of functions αt:C→[0,∞) such that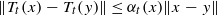 
for x,y∈C. We also demonstrate how the asymptotic aspect of the pointwise Lipschitzian semigroups can be expressed in terms of the respective Fréchet derivatives.
